Output formation tracking for networked systems with limited energy and aperiodic silence
Jin JIN, Junlong LI, Donghao QIN, Ning CAI
a School of Electrical Engineering, Northwest Minzu University, Lanzhou 730030, China
b Key Laboratory of China’s Ethnic Languages and Information Technology for Ministry of Education, Northwest Minzu University, Lanzhou 730000, China
c School of Missile Engineering, Rocket Force University of Engineering, Xi’an 710025, China
d School of Artificial Intelligent, Beijing University of Posts and Telecommunications, Beijing 100876, China
KEYWORDS Energy calculations;Formation;Intermittent working;Networked control system;Tracking
Abstract For leader-following networked systems with the topology switching and the aperiodic silence, limited-energy output formation tracking problems are investigated. Firstly, a new output formation tracking control protocol is proposed, which contains two components associated with the communication interactions between the leader and tracking intelligent agents and the communication interactions among tracking intelligent agents, respectively, and the aperiodic silence, the topology switching and the energy constraint index is introduced properly.Then,a two-step transformation method is presented to separate the whole dynamics of a networked system into the relative dynamics between the leader and tracking intelligent agents and the dynamics of the leader,and sufficient conditions for limited-energy output formation tracking for networked systems with limited energy and aperiodic silence are presented,which are extended into networked systems without the aperiodic silence. Especially, a partition checking algorithm is presented to check limitedenergy output formation tracking design criteria. Finally, a numerical example is illustrated to demonstrate the validness of theoretical results.
1. Introduction
In the past decade, a lot of scientists from different fields paid their attentions to networked systems, which are also called multiagent systems or swarm systems. Networked systems can be applied to explain some natural phenomena, such as flocking.They can also be used to deal with some engineering problems of practical systems,such as coordinated reapplication mote sensing of multiple satellites,consensus of networked systemsand formationor containment controlof multiple unmanned aerial vehicles, where research directions and emphases are different with specific application backgrounds.
For distributed formation control,it is required that multiple intelligent agents form and retain a specific formation structure via local interactions. There are three types of methods to realize distributed formation control; that is, the behavior-based control approach, the virtual-structure-based control approach and the consensus-based control approach.For the behavior-based control approach, intelligent agents may have different manners of behavior according to their operation environment, but it is difficult to establish exact mathematic models. For the virtual-structure-based control approach, there is a virtual node for each intelligent agent to track and all intelligent agents keep a rigid structure, whose robustness is weak as shown in Ref. 15. For the consensusbased control approach, formation control protocols are constructed by using coordinated states and formation functions,and formation design and analysis problems are transformed into consensus design and analysis ones, respectively. Renshowed that the consensus-based control approach can unify the above three methods into the same framework and can give rigorous mathematic analysis with the strong robustness.
Communication topologies depict the local communication relationship among intelligent agents and can be divided into two types: fixed topology and switching topologies, where switching topologies originate from the invalidation of communication equipment or the electronic interference of partial communication channels. Furthermore, network systems can adopt aperiodic silence strategy to countercheck the electronic interference. In Ref. 17, formation control for networked systems with topology switching was addressed and sufficient conditions for formation design and analysis were presented,respectively, where the dynamics of each intelligent agent was modeled by a high-order linear time-invariant system.Wen et al.addressed cooperative control for networked systems with high-order node dynamics and intermittent communication. In Ref. 19, the graph-theory-based controllability complexity caused by adding topology nodes was analyzed and an approach to design topology structures to ensure the controllability under any selection of leaders was presented.Qu et al.investigated Laplacian matrix eigenvalues and eigenvectors based on equivalent partition which are expected to be applied in leader-following consensus control.In Ref.21,limited-budget consensus of multi-agent systems with switching topologies and intermittent communications was investigated and the trade-off design between the energy consumption and the consensus performance was well realized.Qin et al.showed a novel observer-based formation protocol and determined the impacts of the time delay and intermittent communication on formation control of networked systems.In Ref. 23, formation control for cooperative teleoperators was discussed and the influence mechanism of intermittent communications was elaborated.
Moreover, based on the different coordinated variables,there exist two types of formation; that is, state formation and output formation.For output formation,it is needed that partial states or their linear combinations to achieve formation, thus it is more complex to be realized compared with state formation. Ma and Zhanginvestigated formation controllability of networked systems. In Ref. 25, finite-time state formation criteria were presented,where each intelligent agent was modeled by a first-order integrator. An extended-stateobserver method was proposed to deal with robust state formation in Ref. 26. In Ref. 27, a class of distributed state estimators and disturbances estimators were designed to estimate the disturbances and states by using output information of agents for achieving robust consensus. Wang et al.analyzed output formation by the distributed hybrid active control method. According to topology structures, formation control can be categorized as leaderless formation and formation tracking. For the leaderless formation case, all intelligent agents make behavioral decisions by an equal negotiation manner,but for the formation tracking case,it is required that all following agents track the leader with some geometric structure. In Refs. 29–31, state formation tracking problems were investigated, where energy consumption was not considered,but being very important for engineering applications of networked systems. Dong et al.studied guaranteed cost formation tracking, where the energy supply was not determined previously. To the best of our knowledge, output formation tracking for networked systems with the limited energy and the aperiodic silence is still open.
For networked systems with aperiodic silence and the leader-following topology switching, limited-energy output formation tracking control is investigated, where the whole energy supply of all intelligent agents is limited. By two nonsingular transformations, the output of each intelligent agent is separated from its state, and an output formation tracking protocol is presented,which consists of two components corresponding to the non-silent time interval and the silent time interval,respectively.Furthermore,design and analysis criteria for limited-energy output formation tracking are proposed,where the divergence characteristic in the silent time interval is constrained by constructing the relationship of the convergence rate and the silent rate,the influence of topology switching is analyzed by designing a specific common Lyapunov function, and the limited energy is introduced by constructing the relationship between the matrix variable and the limited energy. Moreover, a partition checking algorithm is proposed to check the limited-energy output formation tracking design criteria, and main conclusions for networked systems with the limited energy and the aperiodic silence are extended into the cases without the aperiodic silence.
Compared with closely related works associated with formation tracking of networked systems,the current paper owns the following three critical features. The first one is that the current paper focuses on energy-constraint output formation tracking control for networked systems with switching topologies. In Refs. 29–32, state formation tracking was discussed,which is less general than output formation tracking. The second one is that the impacts of the aperiodic silence are investigated by constructing the relationship of the convergence rate and the silent rate in the current paper. The approaches in Ref. 29–32 cannot be used to deal with networked systems with the aperiodic silence. The third one is that the internal influence mechanism of the limited energy on output formation is analyzed and the relationship between the matrix variable and the limited energy is constructed in the current paper.The impacts of the energy constraint were not considered in Ref. 29–30 and an upper bound of the guaranteed cost was determined in Ref. 32, but this upper bound cannot be given previously and their methods are no longer valid to deal with networked systems with the limited energy.
The arrangement of the current paper is given as follows.In Section 2, the communication interaction topology model and the problem description for limited-energy output formation tracking is presented, where the topology switching and the aperiodic silence are well modeled. Section 3 gives sufficient conditions for limited-energy output formation tracking on the basis of the matrix inequalities and proposes an algorithm to check these conditions.In Section 4,a numerical example is given to demonstrate main results on limited-energy output formation tracking for networked systems with the aperiodic silence. Some summarizations are given in Section 5.
Some key notations are given in Table 1.
2. Topology model and problem statement
2.1. Modeling communication interaction topology
For leader-following networked systems with M agents, the communication interaction topology can be described by a directed graph G with a leader-following structure,where intelligent agent 1 is set as the leader and the other M-1 intelligent agents as tracking intelligent agents with the identical dynamics without loss of generality, which are also called followers.For the directed graph G,each node stands for an intelligent agent, each edge stands for the communication channel between two neighboring intelligent agents, and the edge weight represents the communication strength. It is assumed that intelligent agent 1 can communicate with some tracking intelligent agents, but it cannot obtain coordinated information from tracking intelligent agents.Meanwhile,it is supposed that the communication interaction topology among tracking intelligent agents is bidirectional and the whole topology of a network system has a spanning tree. It can be found that the Laplacian matrix L associated with G has a simple zero eigenvalue with an eigenvector 1. One can refer to Ref. 33 for more details on algebraic graph.

Table 1 Notation index.

2.2. Problem statement
Consider a leader-following networked system with M homogeneous intelligent agents, where intelligent agent 1 is the leader and intelligent agents 2,3,∙∙∙,M are tracking agents. For i=1,2,∙∙∙,M, the dynamics of this networked system is described by



The main objective of the current paper is to determine the design method of gain matrices Kand Ksuch that networked system (1) with protocol (3) achieves limited-energy output formation tracking under the condition that the communication interaction topology is randomly switching and aperiodically silent.

3. Main results
In this section, a two-step transformation method is introduced to separate the whole dynamics of networked system(1) with protocol (3) into two components: the dynamics of the leader and the relative dynamics between the leader and tracking intelligent agents, which are independent with each other. Based on this decomposition, sufficient conditions for limited-energy output formation tracking design and analysis are given, and these conclusions are extended to networked system (1) without the aperiodic silence.
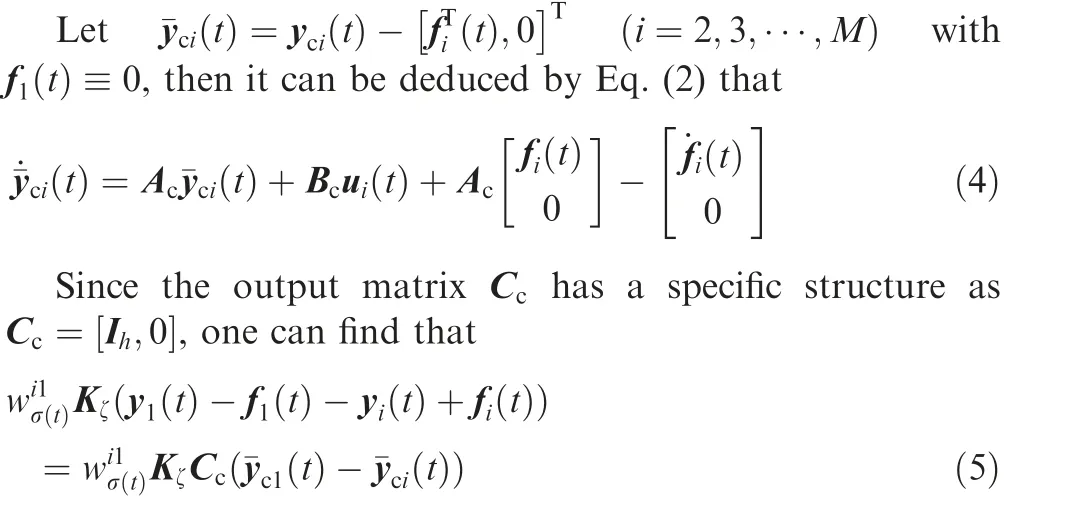




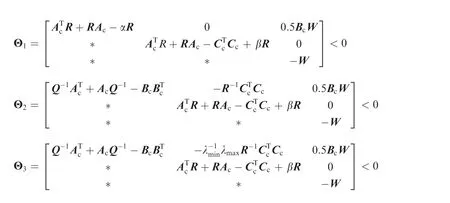
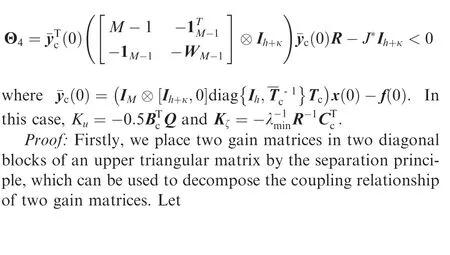
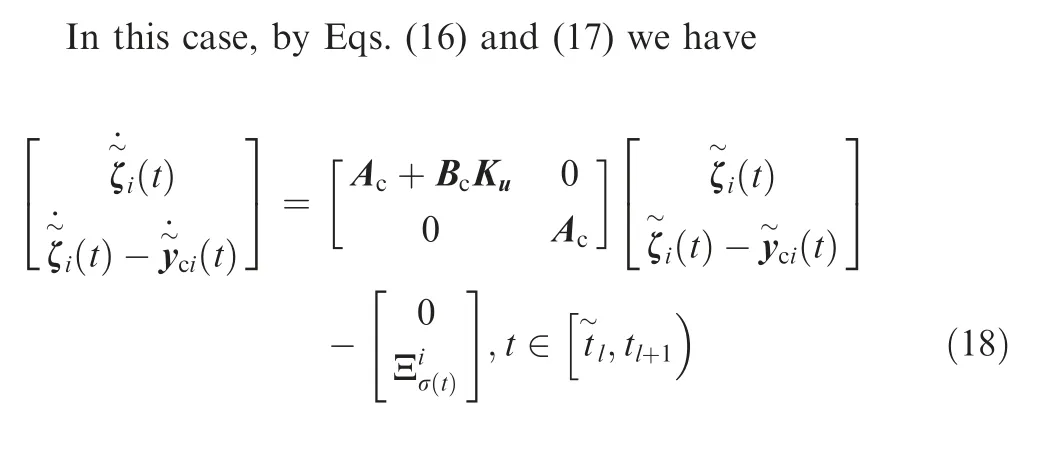






Table 2 Partition checking algorithm.

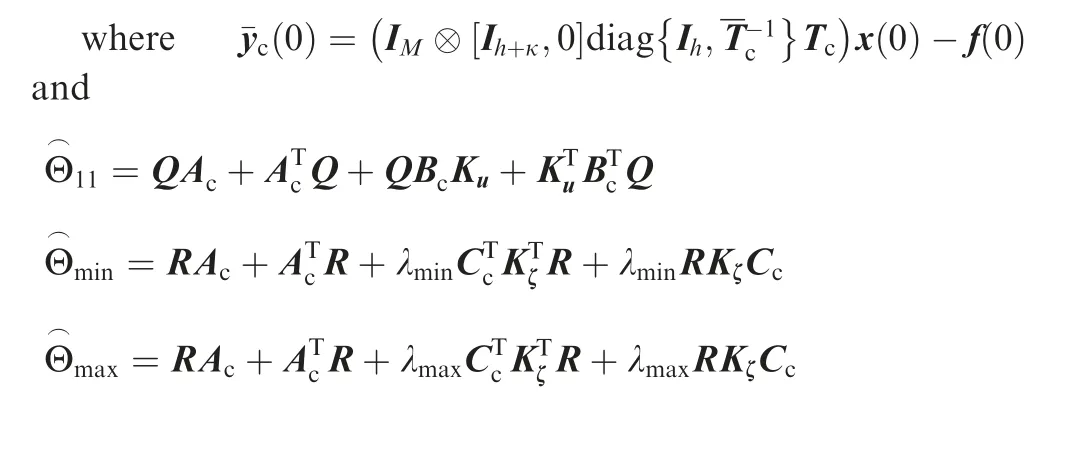
Remark 2. For networked systems with aperiodic silence to realize the output formation tracking, two key challenges are dealt with. The first one is to determine the relative dynamics between the leader and tracking intelligent agents. By the observable decomposition, under the supposition that C is of full row rank, the components related to the output are separated from the state of each intelligent agent. Furthermore,by constructing a time-invariant and a time-varying transformation matrix with special structures, the relative dynamics between the leader and tracking intelligent agents are determined, with the output formation tracking functions involved.The second one is to deal with the impacts of aperiodic silence and limited energy. For networked systems with aperiodic silence, if the motion of each tracking intelligent agent is Lyapunov unstable, then its output may diverge away in the silent time interval, without interactive communications among intelligent agents. By constructing the relationship of the convergence rate and the silent rate, the condition α^ωe<β(1- ^ω) with α>0 and β>0 is introduced to constrain the divergence property in the silent time interval and guarantee the convergence of the global system under the condition that the energy supply is limited. This condition essentially implies that the silent time should be small enough to guarantee the output formation tracking achievement.Especially, Θ<0 in Theorem 1 is used to constrain the impacts of the limited energy. It should be pointed out that this condition disappears when there does not exist the limited energy in networked systems as shown in Theorem 3.

4. Numerical simulation
In this section, an output formation tracking example is employed for illustrating the validness of the proposed control methods in the previous sections.
Example: Consider a networked system consisting of one leader and six followers with aperiodic silence, whose switching communication interaction topology set is depicted in Fig. 1. The dynamics of each agent is described by (A,B,C)that follows:


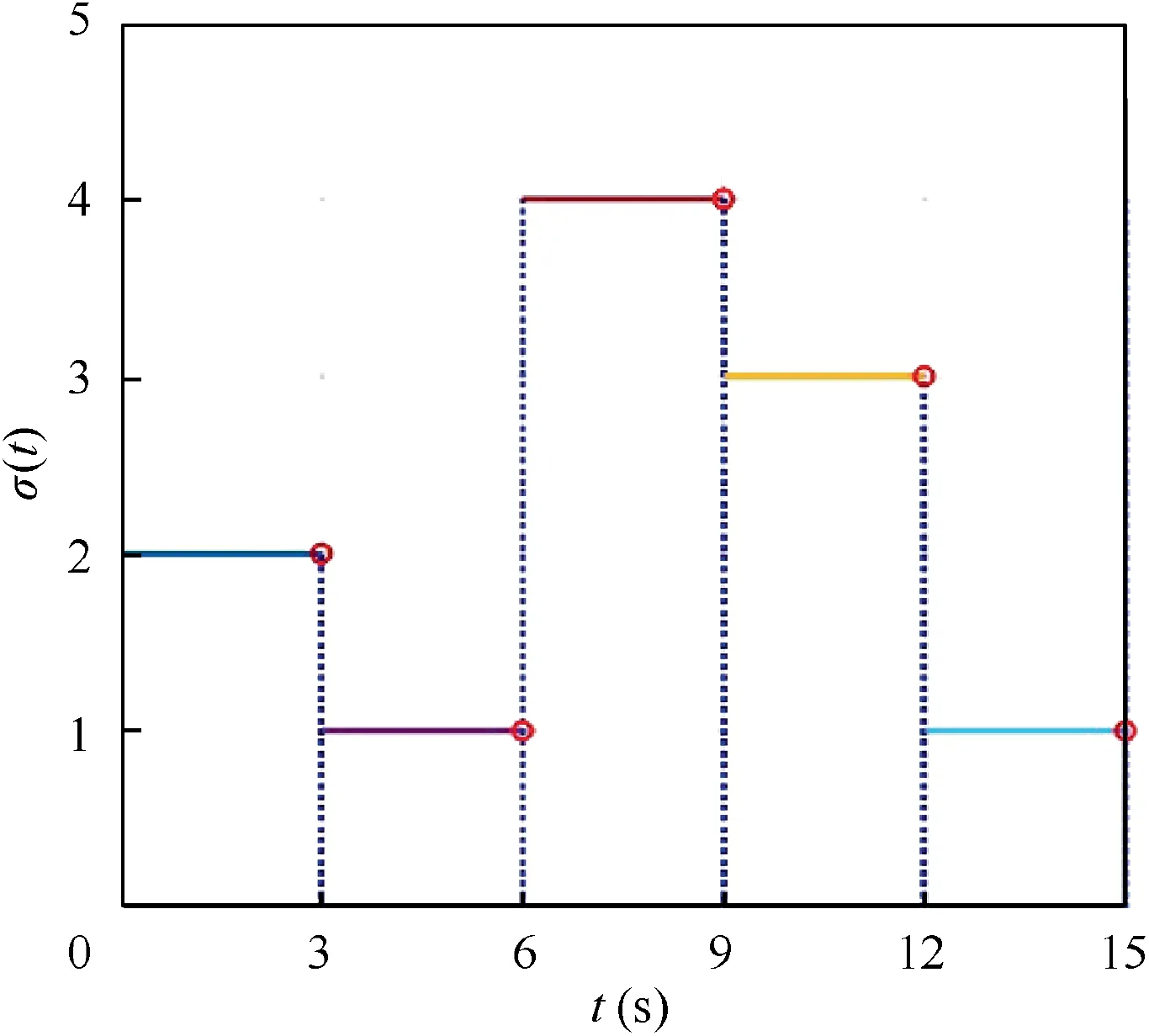
Fig. 2 Switching signal σ(t).
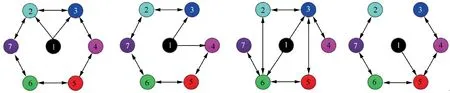
Fig. 1 Switching communication topology set.

The output trajectory snapshots of seven agents with aperiodic silence at t=0 s, t=10 s, t=12 s and t=15 s are shown in Fig. 3, where the single leader and six followers are marked by a hexagram and six different colored circles,respectively.From Figs.3(a)to 3(d),one can see that the desired output hexagon formation is achieved by six followers with the leader locating at the center. Meanwhile, it can be found that the outputs of six followers keep rotating around the leader,reflecting that the formed output formation is time-varying.In Fig. 4, the trajectories of y(t)-f(t) (i=2,3,∙∙∙,7) are depicted, with the red circle markers indicating the trajectory of the leader y(t). One can see from Fig. 4 that y(t)-f(t) (i=2,3,∙∙∙,7) converge to the output of y(t)asymptotically.
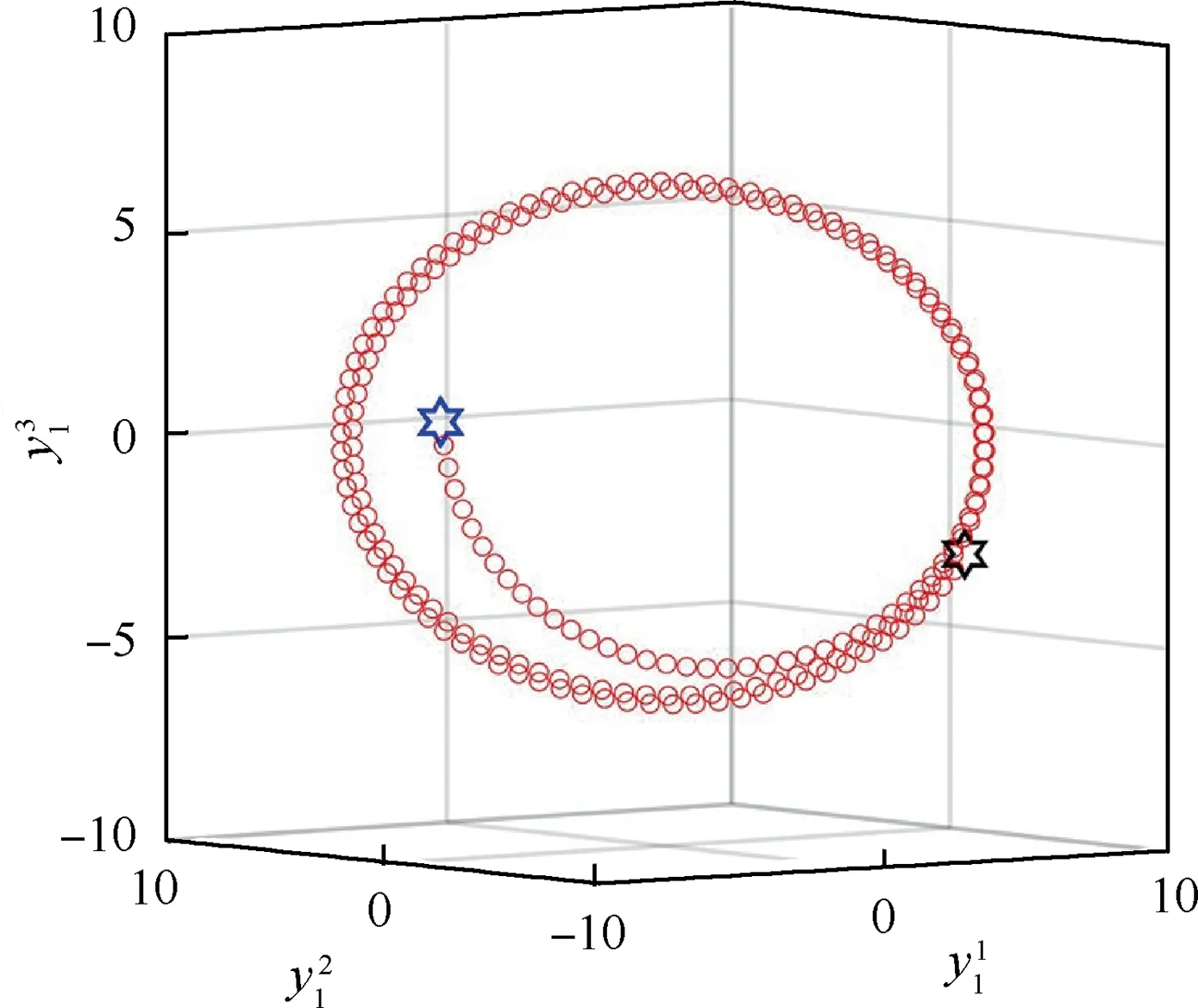
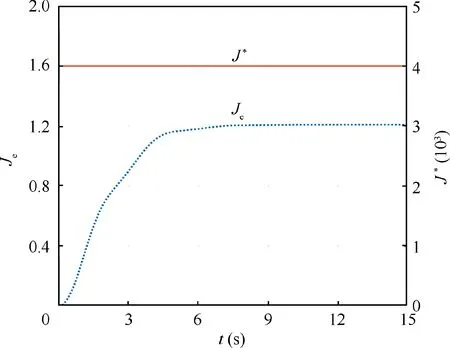
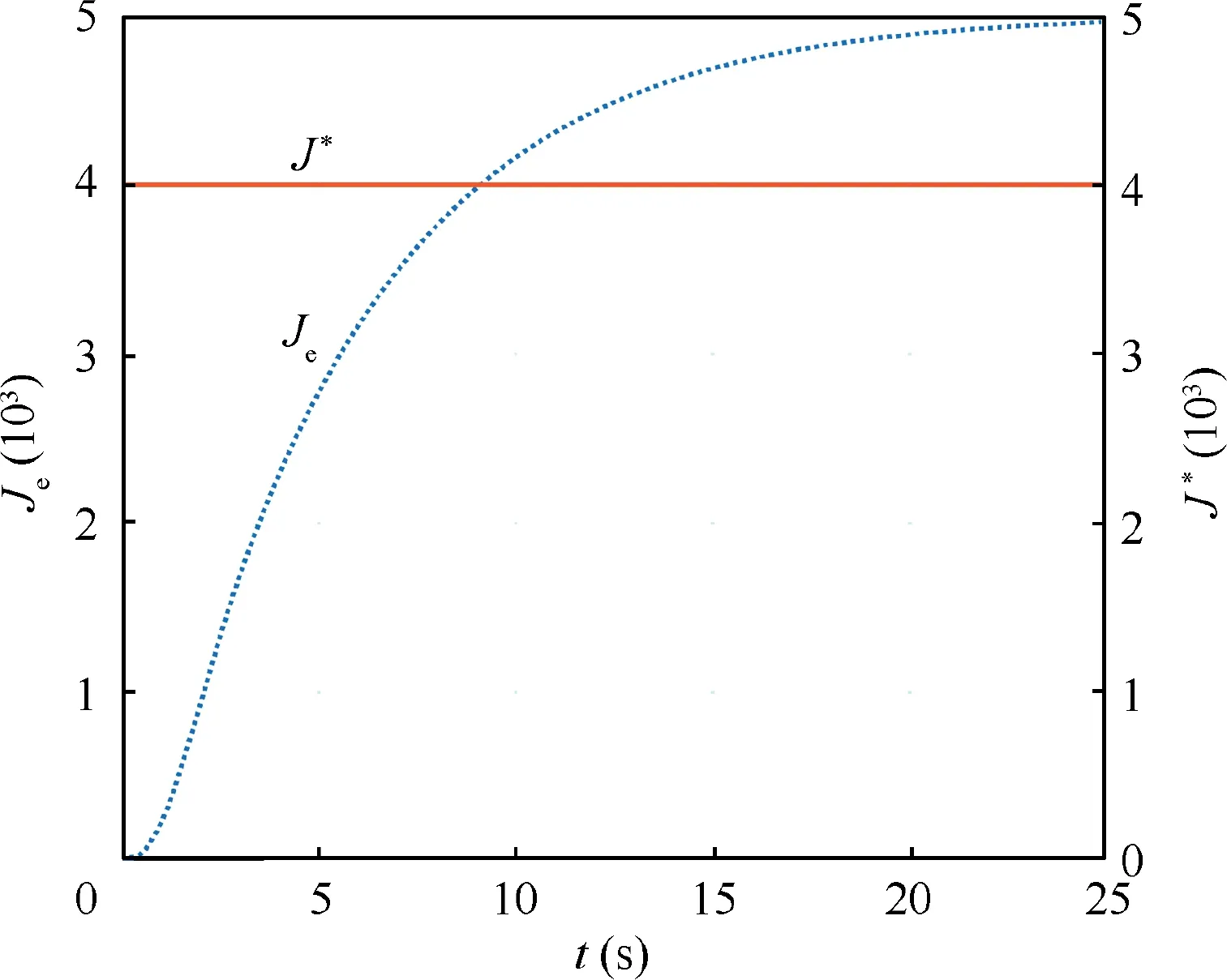
Fig.5 shows the curves of the leader within 15 s,where the initial and final outputs are marked by the blue and the black hexagram, respectively. In Fig. 6, the curves of the whole energy consumption Jand the limited energy supply Jare shown. It can be found that the value of the energy consumption converges to a certain value less than the limited energy supply;that is,J Moreover, without the whole energy supply given, the following gain matrix can be obtained by the associated robust methods with the constraint Θ<0 removed: Fig. 3 Output trajectories of this network system Fig. 4 Trajectories of yi(t)-fi(t) (i=2,3,∙∙∙,7) and y1(t). Fig. 5 Output curves of leader within 15 s. Fig. 6 Curves of the whole energy consumption and the limited energy supply. Fig. 7 Curves of the whole energy consumption and the limited energy supply without the energy constraint term. In this case,Fig.7 illustrates the curves of the actual energy consumption Jand the given energy supply J. One can see that the value of the actual energy consumption is greater than the given energy supply; that is, J>J, showing that the whole energy consumption cannot be constrained and an upper bound of the limited energy can be determined only. For limited-energy networked systems with the leaderfollowing topology switching and aperiodic silence,a new output formation tracking protocol was given, which constructs an energy constraint index to restrict that the whole energy consumption of all intelligent agents being less than the energy supply and satisfying certain separation principle to simplify the design process of gain matrices.A two-step transformation method was employed to transform the output formation tracking problem into asymptotic stability one with aperiodic silence and sufficient conditions for limited-energy output formation tracking design and analysis presented by the linear matrix inequality tool, where the relationship matrix between the matrix variable and the energy supply corresponds to the Laplacian matrix of a star-shaped communication interaction topology with the leader being the central node and all edge weights being one. Especially, the relationship of the convergence rate and the silent rate is introduced to constrain the divergence in the silent time interval, and a partition checking algorithm is proposed to check the limited-energy output formation tracking design criteria. Moreover, these criteria were extended to networked systems without the aperiodic silence.Furthermore, in the future work, we will focus on the aerial vehicles with highly dynamical systems and the aperiodic silence and determine the impacts of the aperiodic silence,the high dynamics and the energy constraint on these systems,where the tracking intelligent agents have different interactive dynamics with the leader. The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. This work was supported by the National Natural Science Foundation of China (Nos. 62176263, 62103434, 62003363,61867005, 61703411), the Science and Technology Nova Plan of Beijing,China(No.Z201100006820122),the Shaanxi Natural Science Foundation for Distinguished Young Scholars,China (No.2021JC-35), the Shaanxi Natural Science Foundation for Youths ,China (No.2021JQ-375), China Postdoctoral Science Special Foundation (No. 2021T140790), China Postdoctoral Research Foundation of China (No. 271004), and the Gansu Provincial First-Class Discipline Program of Northwest Minzu University, China (No. 11080305).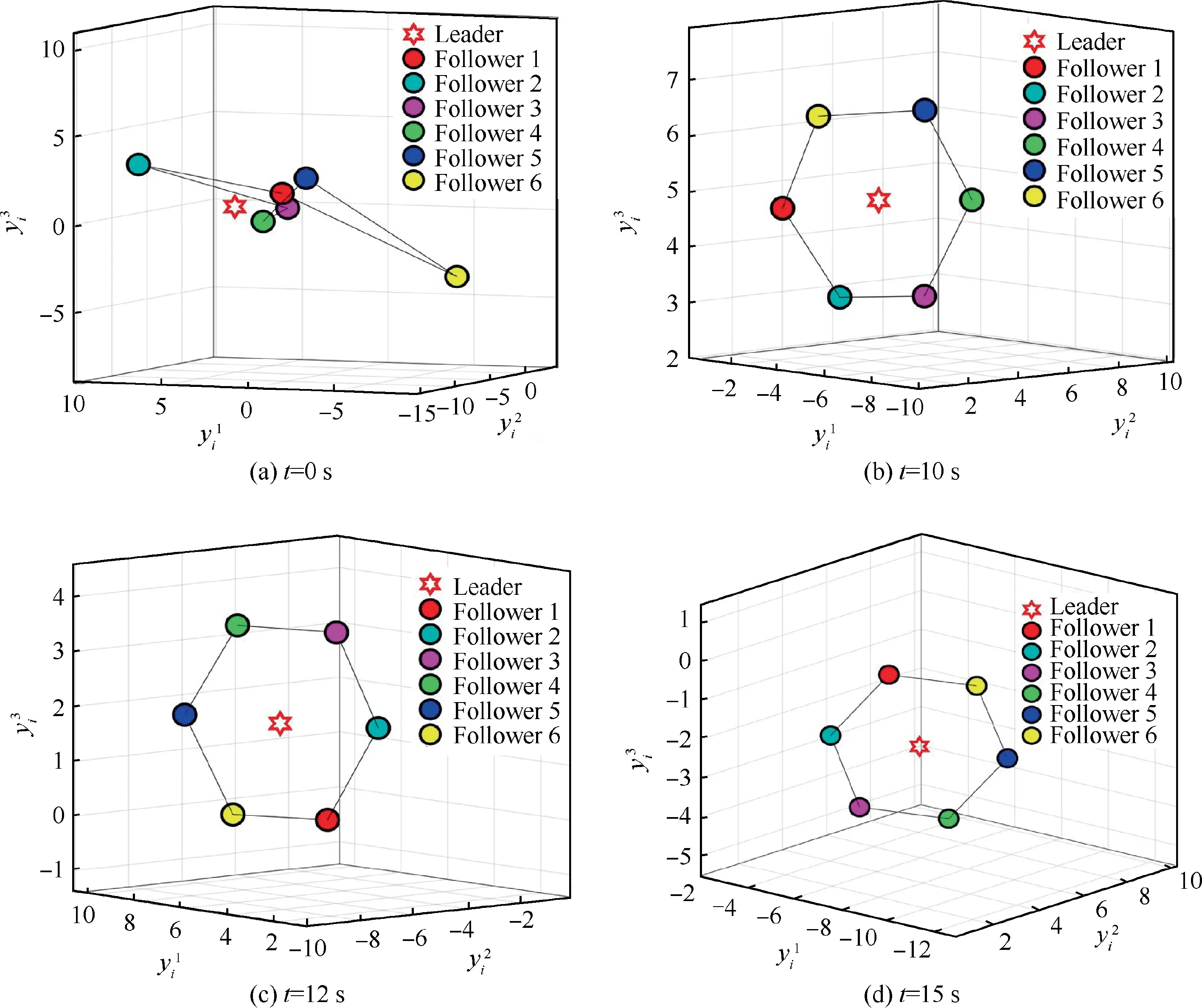



5. Conclusions
 Chinese Journal of Aeronautics2022年7期
Chinese Journal of Aeronautics2022年7期
- Chinese Journal of Aeronautics的其它文章
- An online data driven actor-critic-disturbance guidance law for missile-target interception with input constraints
- Study on excitation force characteristics in a coupled shaker-structure system considering structure modes coupling
- Smooth free-cycle dynamic soaring in unspecified shear wind via quadratic programming
- Active and passive compliant force control of ultrasonic surface rolling process on a curved surface
- High dynamic output feedback robust control of hydraulic flight motion simulator using a novel cascaded extended state observer
- Composite impact vector control based on Apollo descent guidance
