An online data driven actor-critic-disturbance guidance law for missile-target interception with input constraints

Chi PENG, Jinjun MA,*, Xiom LIU

a College of Intelligence Science and Technology, National University of Defense Technology, Changsha 410073, China

KEYWORDS Actor-critic-disturbance structure;Data driven;Differential game;Guidance systems;Input constraints

Abstract In this article, we develop an online robust actor-critic-disturbance guidance law for a missile-target interception system with limited normal acceleration capability. Firstly, the missiletarget engagement is formulated as a zero-sum pursuit-evasion game problem. The key is to seek the saddle point solution of the Hamilton Jacobi Isaacs (HJI) equation, which is generally intractable due to the nonlinearity of the problem.Then,based on the universal approximation capability of Neural Networks (NNs), we construct the critic NN, the actor NN and the disturbance NN,respectively. The Bellman error is adjusted by the normalized-least square method. The proposed scheme is proved to be Uniformly Ultimately Bounded(UUB)stable by Lyapunov method.Finally,the effectiveness and robustness of the developed method are illustrated through numerical simulations against different types of non-stationary targets and initial conditions.

1. Introduction

Proportional Navigation (PN) is extensively used in conventional implementations of homing intercept guidance laws owing to its significant efficiency and simplicity[1–3].The primary goal of PN guidance legislation is to ensure that the interceptor’s rate of turn is proportionate to the interceptor’s Line-of-Sight (LOS) angular velocity relative to the target,and PN has also been proven to be with optimality.[4]Numerous researches, for example, Refs.[5–8] have suggested a variety of different types of modified PN guidance laws for a variety of various circumstances. Behnamgol et al.[9]developed an adaptive finite-time nonlinear guidance law to intercept maneuvering targets in terminal phase and verified the effectiveness of the proposed method both theoretically and numerically.Hu et al.[10]presented two types of guidance laws with impact time constraints for various maneuvering targets based on the idea of sliding mode control. The effectiveness of the proposed method is illustrated via numerical simulations with various velocities and various target maneuvers. However, modern aircraft such as hypersonic missiles and unmanned aerial vehicles have been developing in high speed, high maneuverability, and high concealment, which has brought more challenges to missile-target interception.[11–15] Therefore, it is urgent to introduce new control ideas to deal with targets with high maneuverability.

Recently, zero-sum game applications in missile guidance law have grown in popularity. In a zero-sum game framed by planar pursuit-evasion issue, the missile serves as the pursuer and the target as the evader, resulting in a two-player min–max optimization problem, which is also dubbed as Hproblem in control fields.[16]The objective of a zero-sum game is to determine the Nash equilibrium solution, in which the pursuer seeks to minimize the cost and the evader to maximize the cost. A differential game-based guidance law with a linear quadratic cost for pursuit-evasion interception problem was developed in Ref.[17]. It showed better performance in comparison with classical guidance laws in the simulation scenarios of a pursuer with first-order control dynamics and an evader with zero-lag dynamics. Qi et al.[18] investigated a pursuitevasion guidance law involving three players: an attacker, a target, and a defender. The work in Ref.[19] presented a two-on-two engagement guidance strategy based on norm differential game strategy and linear-quadratic differential game strategy, respectively. However, most of the existing literature assumes the pursuit-evasion intercept model is linearized around the initial collision triangle to simplify the analysis of the problem[17–21]. Due to the intrinsic nonlinearity of the real missile-target pursuit-escape issue, finding the Nash equilibrium requires solving a Hamilton Jacobi Isaacs (HJI) equation, significantly increasing the complexity of finding the global analytic solution; in certain instances, there may be no analytical solution.

Reinforcement Learning(RL),which also emerges as a successful implementation of Adaptive Dynamic Programming(ADP) in control fields, has attracted widespread attention in recent years[22–27]. The fundamental concept behind RL methods is to approximate the Hamilton Jacobi Bellman(HJB)equation using a recursive algorithm such as Policy Iteration (PI) or Value Iteration (VI)[23]. Then an actor-critic Neural Network (NN) structure is built, consisting of a critic NN for cost function approximation and an actor NN for control policy approximation. Generally, the conventional approach updates the weights of the actor and critic networks progressively until they converge to a stable value.Vamvoudakis and Lewis[28] proposed an online PI algorithm to adjust the weights of the actor NN and the critic NN simultaneously and called it ‘synchronous’ policy iteration. In a two-player differential game problem, the application of the actor-criticdisturbance NN structure has recently evolved as an efficient method for approximating the solution of the HJI equation.

On the basis of previous work, Vamvoudakis and Lewis expanded their approach to the differential game and constructed an actor-critic-disturbance NN structure with weights updated concurrently,demonstrating that the closed-loop nonlinear system is Uniformly Ultimately Bounded(UUB)stable.[29] Additionally, many recent works have been significantly expanded on this premise.For instance,Lv et al.[30]proposed a model-free Hcontroller based on the identification of neural network systems. Zhao et al.[31] suggested an eventtriggered actor-critic-disturbance dynamic programming controller in order to address the problem of limited computer resources. In terms of constrained systems, an appropriate non-quadratic barrier function is usually incorporated into the cost function to account for input saturation in the actor-critic architectures. Modares presented an online learning algorithm for finding the saddle point solution for continuous-time nonlinear systems with input constraints.[32]Taking the system with full-state constraints and input saturation into consideration, Yang et al.[33] developed an online barrier-actor-critic learning control strategy for differential games to fulfill the requirement of the state constraint by introducing the technique of system transformation. However, the system transformation technology has a drawback in that it is usually successful only for simple state restrictions and may cause the control input to tend to infinity as the state approaches the boundary.

Although there have been extensive studies on the reinforcement learning control design of zero-sum games, few discussions on guidance laws in this area have been discussed.Sun et al.[34–38] integrated ADP technology with the backstepping method, fuzzy logic units, and other techniques and made significant contributions to the guidance law’s architecture. However, these researches only take the application of a single critic network to the proposed methodology. And in most single critic NNs related works,there are no strict proofs,and simulation results have been provided to guarantee that the NN weights converge to the actual value.[32,33,39–41]As a result, it is necessary to introduce additional NNs in the control structure to ensure the convergence of closedloop system parameters.

Inspired by the aforementioned literature, considering a missile-target interception system in the presence of input constraints, we develop a novel online least-squares-based actorcritic-disturbance guidance law in this paper. First of all, the missile-target engagement problem is formulated as a differential game mathematical model and a HJI equation is produced.Then we construct an actor-critic-disturbance structure based on NN to approximate the optimal solution of the HJI equation online. It is worth noting that persistence of excitation condition is necessary to guarantee convergence of obtaining the optimal saddle point solution.

The main contributions of the proposed method can be summarized as follows:

(1) In contrast to the conventional offline design of guidance law, we summarize the guidance problem with unknown maneuvering targets into an online solution problem within the framework of differential game. On this basis, a missile guidance scheme based on actor-criticdisturbance structure is constructed. The stability of the closed-loop system is demonstrated by Lyapunov method.(2) The proposed method takes into account the realistic limitations of normal acceleration of missiles. By introducing a smooth non-quadratic penalty function associated with the control policy,we ensure the continuity of the system with input saturation.

(3) A variety of maneuvering targets are tested for the developed online guidance law. Unlike the assumptions that the target maneuver is known in Ref.[35], despite the absence of the information of the target acceleration with various forms(such as sinusoidal maneuver,square maneuver, etc.), the proposed approach improves the guidance system’s performance when confronted with unknown maneuvering targets.

The remainder of the paper is organized as follows:In Section 2, the missile-target interception engagement is formulated, and some relevant preliminaries are given. In Section 3, the two-player differential game guidance law is designed and proved. In Section 4, numerical simulations are presented and discussed. Conclusions are drawn in Section 5.

2. Problem statement and preliminaries

2.1. Missile-target engagement formulation

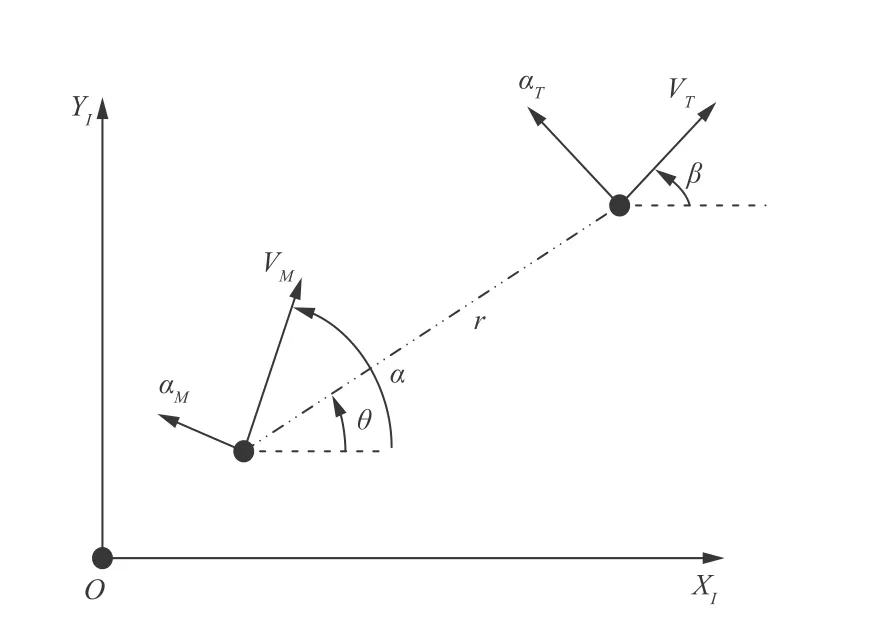
Fig. 1 Missile-target engagement geometry.

Remark 2. Through the comparison shown in Fig.2,it can be seen that the constraints adopted in this paper not only strictly guarantee the boundlessness of the control input, but also ensure the continuity of the system dynamics.

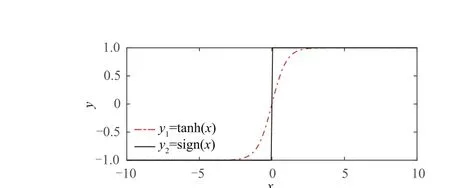
Fig. 2 Comparison between two amplitude-limiting functions.

Then the missile-target engagement problem with normal acceleration saturation can be re-described as a Hcontrol problem of a differential game with input constraints.The controlled target is to ensure that the missile can accurately hit the target under unknown maneuverability.

2.2. Lemmas, assumptions and definitions

Remark 3. It is necessary to satisfy the PE condition in adaptive control.[42] And it is needed in this research because one desires to identify the critic NN weights by normalized leastsquares adaptive law to approximate the cost function V(x ).

Definition 2. (Bellman’s Optimality Principle)An optimal policy has the property that no matter what the previous control actions have been, the remaining control actions constitute an optimal policy with regard to the state resulting from those previous control actions.Consider nonlinear discrete-time system dynamics as followings

Definition 3. (Admissible Policy Set) A control policy u(t ) is said to be admissible on Ω,if the dynamics of closed-loop system Eq.(10)are stable and the cost function V(x )for the given set have finite value.

Remark 4. Among the above assumptions,Assumptions 1,2 are universal in the control system.In Assumption 3,which is quite different from the Ref.[35],it is a relatively relaxed condition to assume that the upper bound of the target maneuver is an unknown constant. Assumption 4 can be satisfied based on Weierstrass high-order approximation theorem.

3. Design of guidance law

Consider the nonlinear continuous-time system with external disturbances described in Eq. (6), for an admissible control policy, the cost function can be employed as

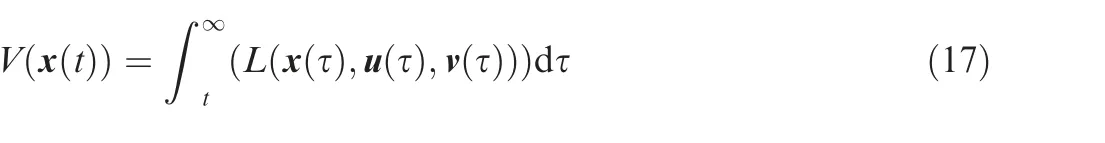
Remark 5. Due to the nonlinearity of Eq. (25), it is usually intractable to obtain its analytical solution.In order to find the Nash solution u,v( ) of the two-player differential game, a policy iteration algorithm based on the idea of reinforcement learning is proposed.[16] The disturbance and control policies are iterated in sequence by constructing the inner and outer loops until the optimal saddle point solution is obtained. It is noted that the interference strategy and the control strategy in the PI algorithm proposed in Ref.[16] are not performed simultaneously and are calculated offline, which is not helpful to cope with the actual situation.Following that,we propose a data-driven adaptive iterative algorithm based on NNs to solve the Hcontrol problem with input constraints.

Remark 7. It should be noted that the above update law cannot be directly applied to the update of the control because it cannot guarantee the stability of the entire closed-loop system. To ensure stability in the sense of Lyapunov, we will make some modifications in the following work.

Remark 8. In this research,the least-squares-based update law is used for critic NN weights, and the gradient-based update laws are used for actor and disturbance NN weights. The forgetting factor ξ is used to ensure that the adaption gain Γ(t )is positively definite along the time. Therefore, Γ(t ) can be bounded as Γ≤Γ(t )≤Γ, ∀t>0.

Now we propose the main theorem to discuss the stability of the closed-loop system with input saturation.

Theorem 1. Consider the nonlinear dynamics described in Eq.(6)for the missile-target engagement problem.Assumptions 1–4 are held. The critic-network, actor-network and disturbancenetwork are updated as Eqs. (36), (38) and (39), respectively.The signal βis assumed to be persistently exciting. Then the closed-loop system states and the weights errors of three interconnected networks are UUB.

Proof. Consider the continuously differentiable, positivedefinite Lyapunov candidate function as follows:

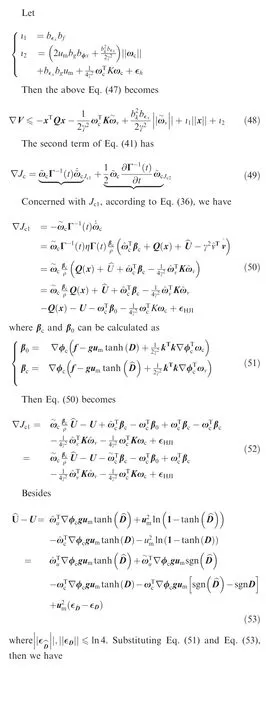
It is verified that the system state and the NN weights are UUB, and the proof is completed. □

Remark 9. From the aforementioned analysis,we can see that the parameter ıcontains systems information β,which shows that the PE condition is critical to guarantee the convergence of the system.

To this point, we have finished the design process of the guidance law, and the guidance architecture of missile interception mission is shown in Fig. 3. The proposed framework is made primarily of three networks:an actor network,a critic network, and a disturbance network. The actor network is used to generate guidance law in real time,the disturbance network is used to determine the target’s escape acceleration,and the critic network is used to evaluate the present strategy’s performance. Finally, th interception mission is accomplished via the online computation between the missile and the target.

4. Simulation

In this section, we will illustrate the effectiveness of the proposed method through the following target maneuvers in various scenarios.

The initial conditions of the missile and target are described in Table 1. And the design parameters of the control scheme are shown in Table 2.

In the following, three scenarios are studied to show the competitive performance.

4.1. System with differential game-based maneuvering target

In this scenario, the proposed guidance law is applied to the system with differential game-based maneuvering target to examine the performance.The missile is assumed as a pursuer,and the target is assumed as an evader, where initial parameters are given in Table 1.The activation functions need to satisfy the assumptions discussed previously, such as Sigmoid functions,radial basis functions(RBFs),etc.Herein we choose activation functions as polynomial functions

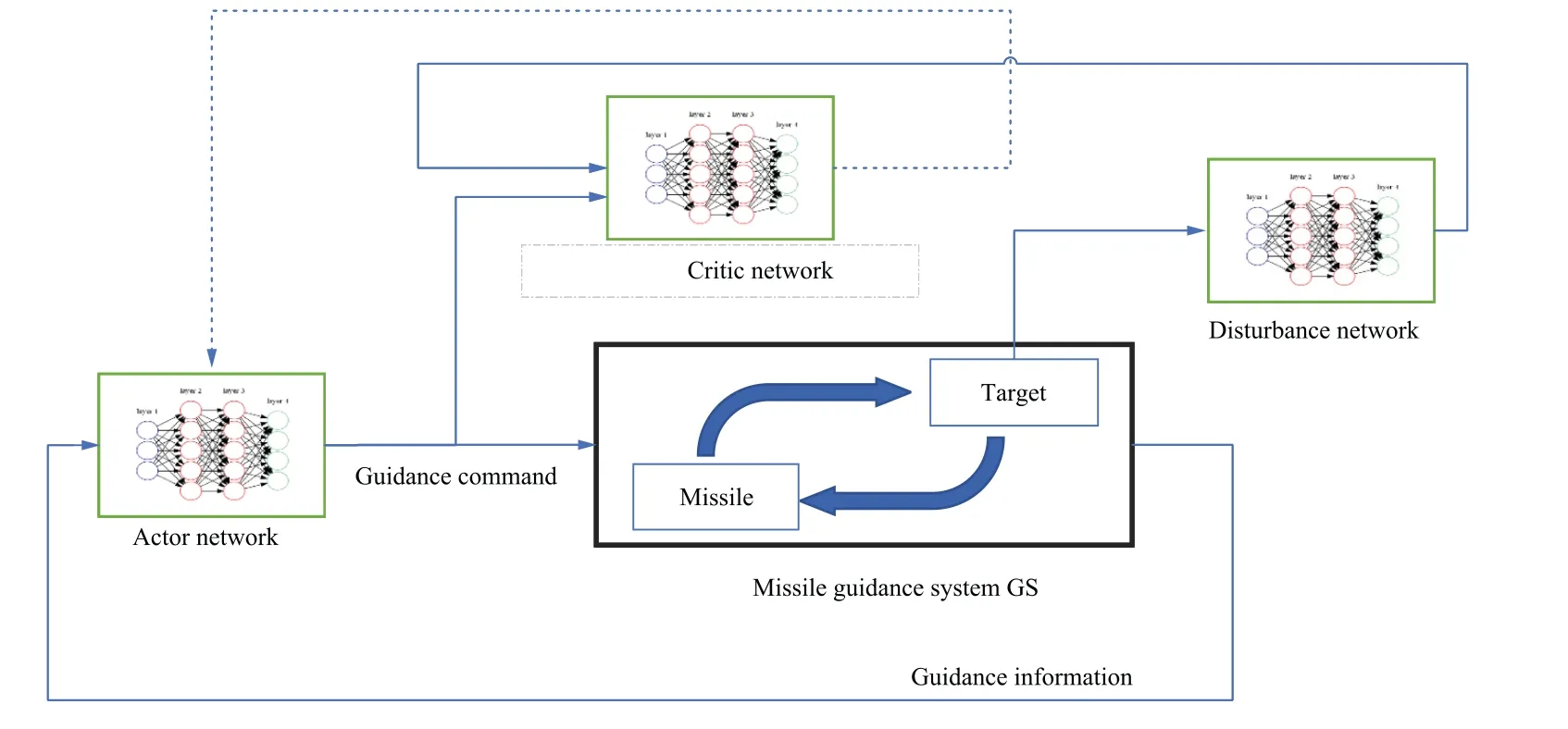
Fig. 3 Guidance architecture of missile interception mission.

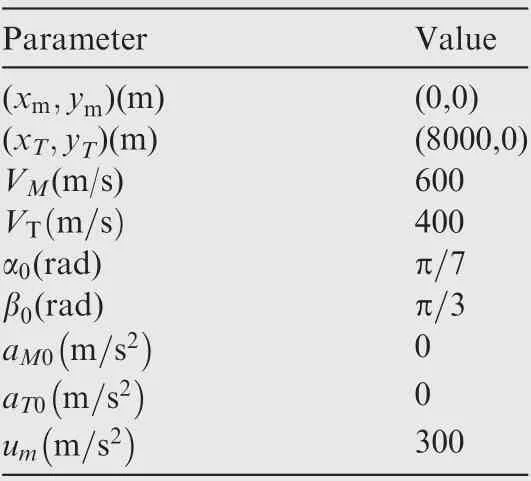
Table 1 System parameters of the missile and target.

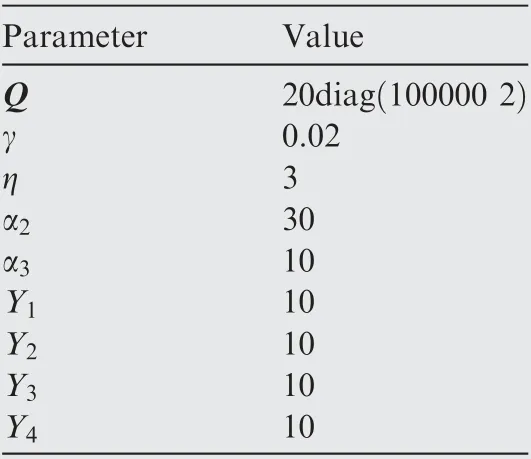
Table 2 Design parameters of guidance scheme.

To guarantee that the PE condition is satisfied, a small probing noise is added to the input signals in the learning phase t ∊[0,15] s. The NNs weights are initialized randomly during the range.

Fig. 4 describes the missile-target intercept geometry with the proposed approach,and it is showed that the missile could hit the target with the intelligent escape ability. Fig. 5 shows the control policy of limited normal acceleration.In Fig.6,system state of missile-target dynamic are given.Additionally,the convergence of actor-critic-disturbance structure can be obtained from Figs. 7- 9.

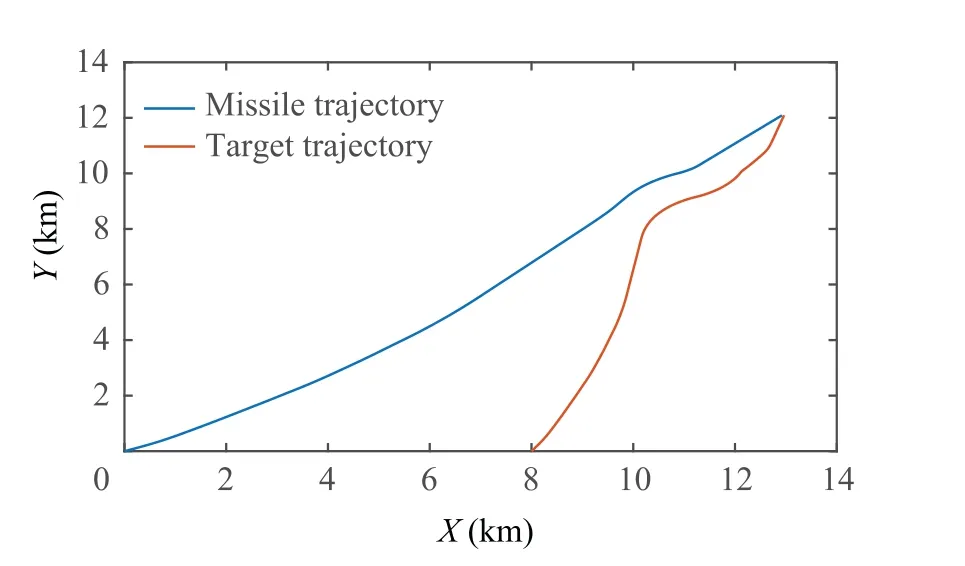
Fig. 4 Missile-target interception trajectory.

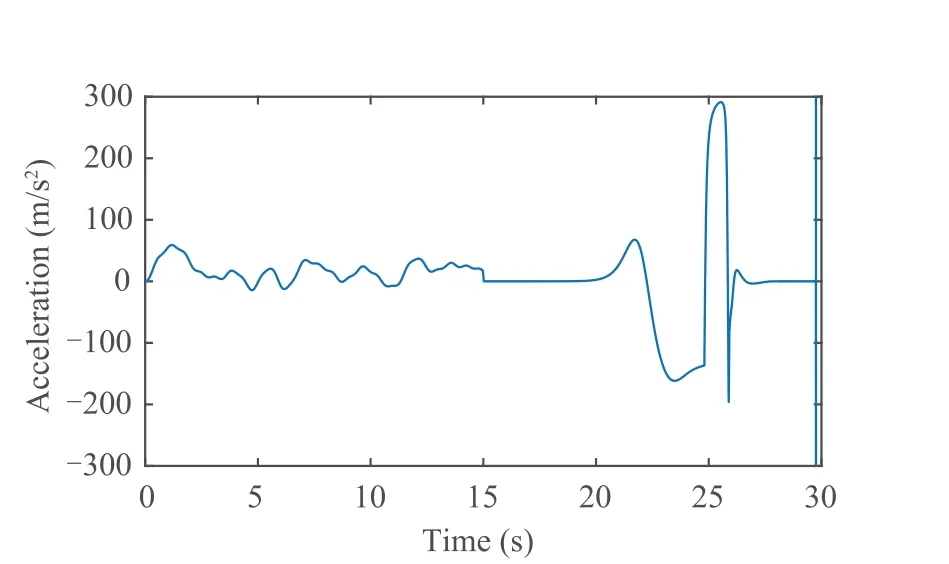
Fig. 5 Normal acceleration of missile.

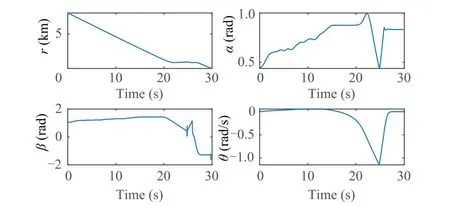
Fig. 6 System state of missile-target dynamics.

For comparison, we consider the case of no input constraints, and the simulation results are shown in Fig. 10 and Fig. 11. It can be seen that, in the same simulation environment, if the input signal is not designed with corresponding constraints in the cost function, the normal acceleration will exceed the available acceleration, which may directly lead to the failure of the interception mission.

The missile-target interception geometry with the suggested method is shown in Fig.4,and it demonstrates that the missile may strike the target with the intelligent escape capability.The control strategy of restricted normal acceleration is shown in Fig.5.The system state of the missile-target dynamics is shown in Fig. 6. Additionally, Figs. 7–9 illustrate the convergence of the actor-critic-disturbance structure.

Furthermore, we examine the situation of no input restrictions for comparison, and the simulation results are presented in Fig.10 and Fig.11.As can be observed,if the input signal is not constructed with appropriate cost function restrictions,the normal acceleration will exceed the allowed acceleration,which may directly lead to the failure of the interception mission.

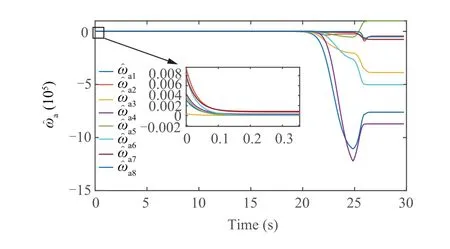
Fig. 7 Update of actor NN weights.

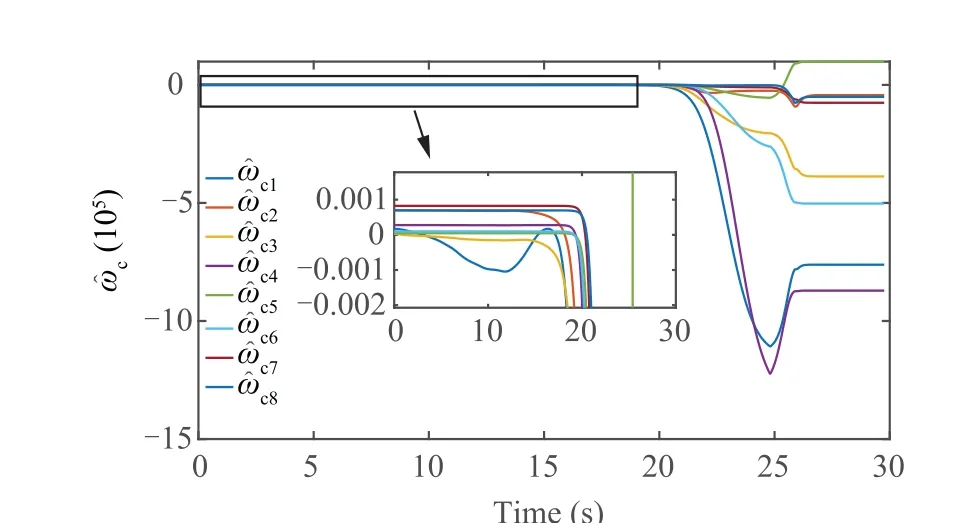
Fig. 8 Update of critic NN weights.

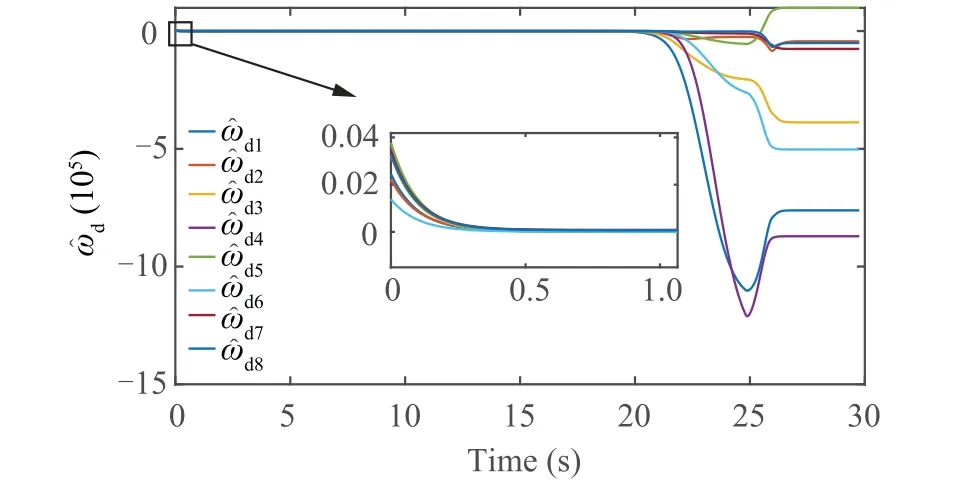
Fig. 9 Update of disturbance NN weights.

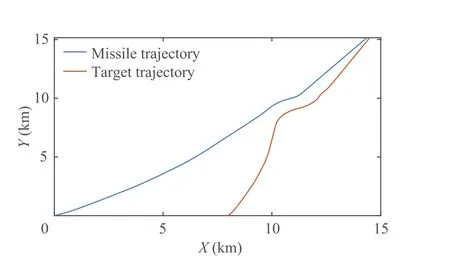
Fig. 10 Missile-target Interception trajectory without input constraint.

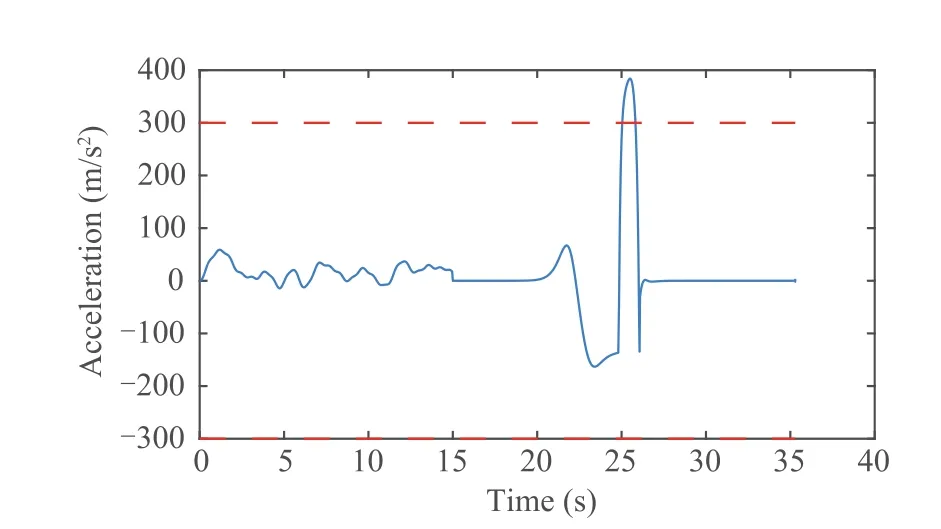
Fig. 11 Normal acceleration without input constraint.

4.2. System with different maneuvering targets

In order to simulate as much as possible the targets with complex maneuvers in the actual interception process,we take different maneuvering targets into account and treat them as an unknown external disturbance to verify the robustness of the proposed method.The simulation considers sine-wave maneuvering targets, square-wave maneuvering targets, and hybrid maneuvering targets with different frequencies. Same as mentioned above, the online learning process is chosen as t ∊[0,10] s with a slight probing noise.

Figs. 12 and 13, illustrate the results. As can be observed from the comparison of these figures, the suggested approach demonstrates greater robustness when confronted with a variety of moving objects of varying shapes. As shown in the preceding simulation, the suggested online differential game guidance rule exhibits an amazing level of robustness.It is cap-

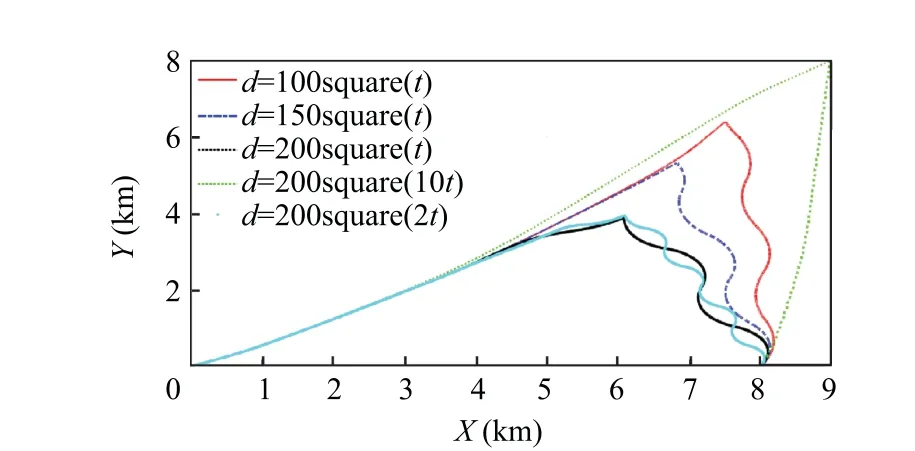
Fig.12 Performance under various square maneuvering targets.

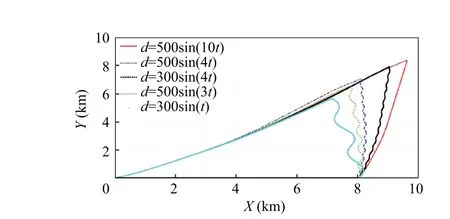
Fig. 13 Performance under various sinusoidal maneuvering targets.

able of intercepting not just cognitively evasive targets, but also ones with unknown and complicated maneuverability.

4.3. System with different initial conditions

In this part,in order to further illustrate the effects of different initial conditions of the guidance system on the proposed method, we consider the different initial flight path angle of the missiles (α), the initial heading angle of the target (β),and the speed of the missile and the target(V,V)in following simulations. The maneuver of the target is assumed to be a sine-wave disturbance d=300 sin (2t ). Same as the previous simulations, the learning process is chosen as t ∊[0,10] s with a small probing noise.The performance of the guidance system is shown in Fig. 14–17.

4.4. Comparison with proportional navigation law

Finally, we compare the proposed guidance law with the popular PN law. According to the idea of PN law, its normal acceleration command can be written as u=Nx=Nσ.

Fig.14 Performance under various hybrid maneuvering targets.

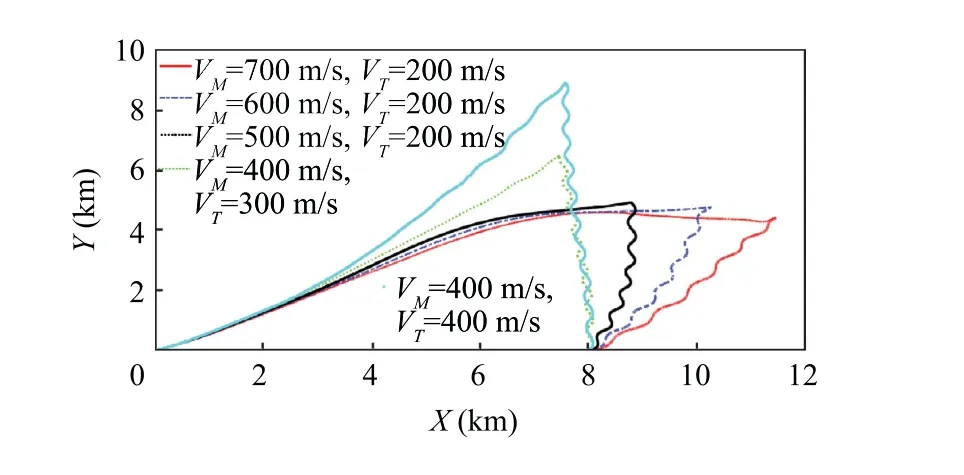
Fig. 15 Missile-target interception trajectory with different velocity.

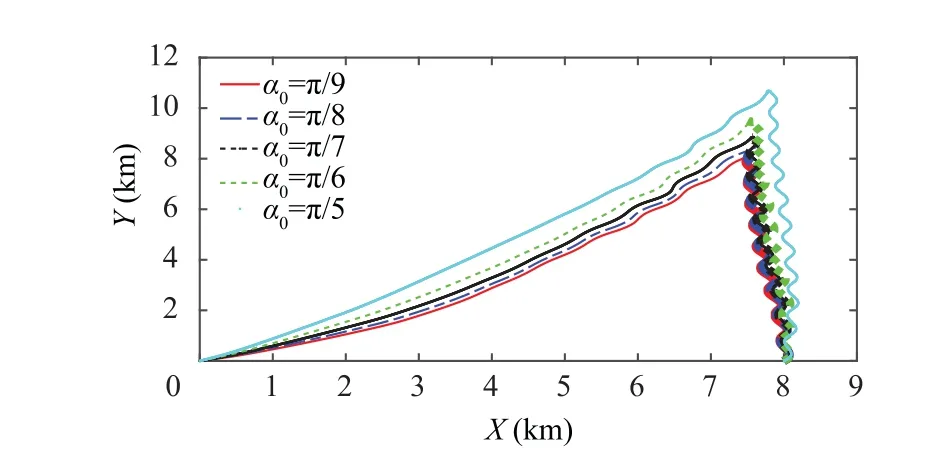
Fig. 16 Missile-target interception trajectory with different α0.

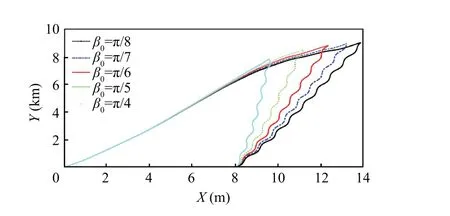
Fig. 17 Missile-target interception trajectory with β0.

To conduct a realistic analysis,the guidance parameters are listed in Table 1,and the maneuver of the target is assumed as d=200square(5t ). At the same time, in order to reflect the effect of the algorithm online learning time t, the cases of t=10 s and t=8 s are considered respectively. The coefficient of PN algorithm is reasonably set as N=400.

For convenience, the proposed method is named Actor-Critic-Disturbance Guidance (ACDG) law. The simulation results are shown in Fig. 18. The simulation indicates that guidance time of ACDG was 24.5 s,whereas the guidance time of PN was 25.5 s.Additionally,it can be seen from Fig.19 that the ACDG has lower normal acceleration in the guidance process, implying that it has more adjustment flexibility.

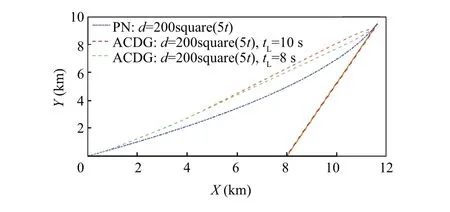
Fig. 18 Missile-target interception trajectory with different guidance laws.

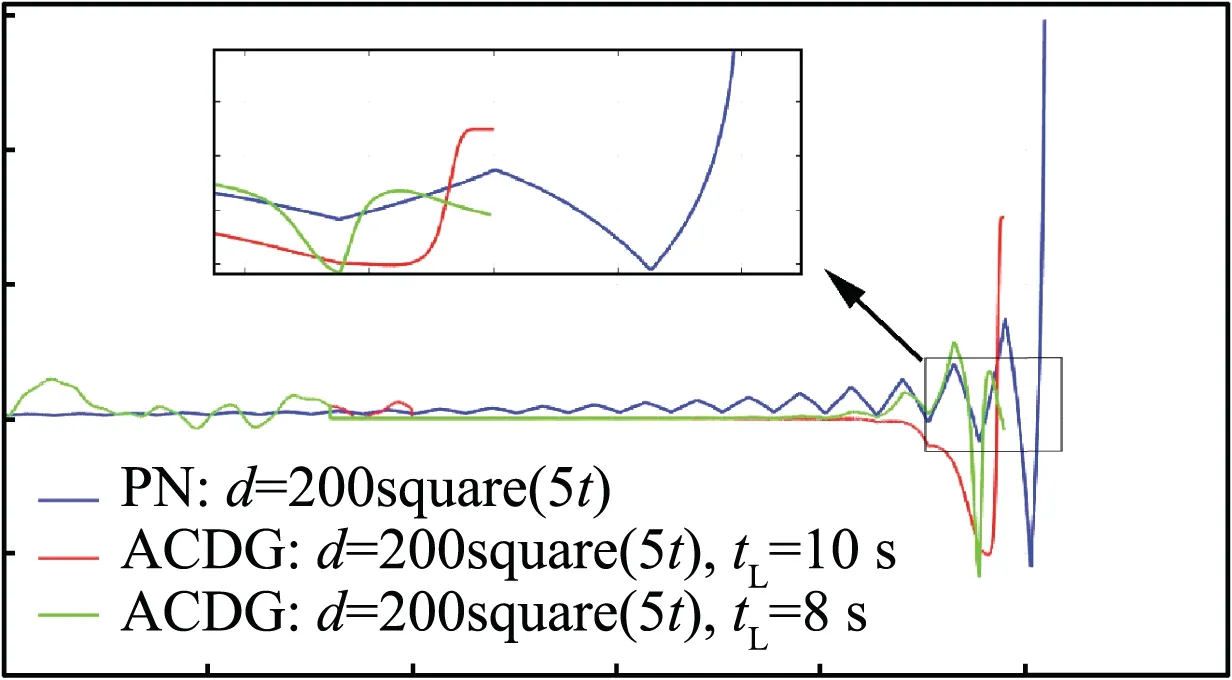
Fig. 19 Normal acceleration with different guidance law.

5. Conclusions

This paper presents an online robust adaptive actor-criticdisturbance learning guidance law with input constraints aimed at a one-on-one planar missile-target pursuit-evasion problem. Unlike the previous guidance law design, we first assume that the maneuvering target is an agent with evader capability and build a differential game problem. Then, considering that there is a limited normal acceleration in the actual guidance design problem,we add a smooth saturation function about the input to the design of the cost function.According to the simultaneous tuning of the actor-critic-disturbance NNs structure, the proposed approach can converge to the nearly optimal solution.After showing the detailed theoretical analysis by Lyapunov method, the proposed guidance scheme is applied to the missile-target engagement in numerical simulations and demonstrates the effectiveness.

As far as we are aware, the present guidance law design rarely involves research on collision avoidance, although it does exist in a complicated chaser-evader environment. At the moment, the Control Lyapunov Function (CLF) method has made significant progress in collision avoidance of the robot control, which provides as motivation for our work.[44,45] In future work, we intend to integrate the suggested method with the CLF method to examine the design of online data-driven guidance laws in complex settings in more depth.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This study was partially supported by the National Natural Science Foundation of China (Nos. 61203095 and 61403407).