Smooth free-cycle dynamic soaring in unspecified shear wind via quadratic programming
Haichao HONG, Benedikt GRU¨ TER, Patrick PIPREK, Florian HOLZAPFEL
Institute of Flight System Dynamics, Technical University of Munich, Garching D-85748, Germany
KEYWORDS Dynamic soaring;Optimal control;Quadratic programming;Trajectory generation;Trigonometric series
Abstract Harvesting wind energy is promising for extending long-endurance flights,which can be greatly facilitated by a flight technique called dynamic soaring. The presented study is concerned with generating model-based trajectories with smooth control histories for dynamic soaring maneuvers exploiting wind gradients. The desired smoothness is achieved by introducing a trigonometric series parameterization for the controls,which are formulated with respect to the normalized time.Specifically,the periodicity of the trigonometric functions is leveraged to facilitate the connection of cycles and streamline the problem formulation. Without relying on a specified wind profile, a freefinal-time quadratic programming-based control strategy is developed for the online correction of the flight trajectory,which requires only the instant wind information.Offline and online numerical studies show the trade-off to achieve the smoothness and demonstrate the effectiveness of the proposed method in a varying wind field.
1. Introduction
Since the first observations of the flight of albatrosses by Rayleighin 1883,dynamic soaring,which is a flying technique that some birds perform to extract kinetic energy from the moving air to support their long-endurance flights, has interested the research community continuously.Theoretical analysis of the flight mechanics of dynamic soaringand advancements in computational capacity made it possible to perform numerical optimization.These have sparked the determination of transferring the flight pattern from birds to aircraft, especially Unmanned Aerial Vehicles (UAVs).
Offline studies rely on prescribed wind profiles. However,accurate modeling of the complete shear wind profile is not feasible in real world, especially for real-time tasks. Efforts to overcome this caveat by introducing online wind estimation are undertaken in Ref. 16. The authors propose a closed-loop control system including a wind estimation based on the aircraft states,which is used to re-optimize the trajectory considering current wind conditions. A feedforward-feedback controller is used to track the planned trajectory, reusing the results from the trajectory planner as feedforward commands.The problem is also addressed in Ref. 17 constructing a parameter-dependent representation of the flight path, and a deep neural network is utilized to adjust the parameterized flight path according to the wind conditions. In Ref. 17, the direct control inputs are determined by a path-following controller.Therefore,the correction of the trajectory and the generation of control commands are separated, which facilitates the deployment of different path-following controllers.Nonetheless, to follow a desired trajectory requires the corresponding agility of aircraft.Taking the aircraft dynamics into consideration might enhance the general performance. In this regard, yet another characteristic that can be improved in the field of dynamic soaring trajectory generation is the smoothness of the control inputs. The controls, e.g., the lift coefficient and the bank angle, account for the flying and lift-generating mechanism. In principle, steps in control histories are undesirable, or even unachievable. However, with the exception of Ref.17,most existing studies utilize optimal control methods that do not emphasis such a requirement.
The presented study of dynamic soaring trajectory online generation in an unspecified shear wind profile is originated in Ref. 18. Here, an approximation of the wind strength variation is introduced and utilized in a convex optimization formulation with control constraints for online correcting the soaring trajectory in an unspecified wind profile.The optimization formulation in Ref. 18 considers a fixed final time, so the cycle time is fixed and needs to be specified. In addition, the smoothness of control variables cannot be guaranteed. Furthermore, state constraints, such as the altitude constraint,cannot be considered. A trigonometric series-based smooth trajectory generation method is developed in Ref. 19: These controls, being infinitely differentiable and analytically defined, render more practical applicable commands and thus higher availability of the trajectory. Moreover, constraints on control derivatives can be incorporated without introducing new variables. These features may enable a smooth dynamic soaring trajectory that can be readily implemented. However,a free cycle is yet to be realized. Therefore, this paper aims at enhancing the previous solution by addressing these concerns. First, the trigonometric series design is applied to parameterize the control variables for obtaining the smoothness. The series are formulated with respect to the normalized time in order to cope with the free final time. Moreover, the period of the series is designed to be the same as the cycle time so that the controls and control derivatives are equal at the boundary points, which enforces smooth connections of dynamic soaring cycles. An offline simulation study compares the minimum wind strengths required by performing an energy-neutral cycle for the full discretization and for the trigonometric series design. Second, the relationship between the wind strength variation and the variation of the trajectory is derived. The wind strength variation is determined by the changes of the reference wind speed in a nominal wind model.The variation of the trajectory includes the incremental changes of states, controls, replaced by the series coefficients,and the final time. This relationship is considered in a strictly convex Quadratic Programming (QP) formulation with all constraints converted to forms with respect to the increments.Third, solving the QP problem yields an updated soaring trajectory with a new cycle time, for which only instant wind information are needed instead of the complete wind profile.This process is repeated to continuously update the trajectory.Online trajectory correction studies are conducted to show the effectiveness of the proposed method, where wind measurement errors are considered as well.
The contributions of this paper are summarized as follows:(A) The trigonometric parameterization of the controls is applied for generating dynamic soaring flight trajectories with smooth controls. (B) The proposed series design takes advantage of the periodicity of trigonometric functions to simplify the implementation of boundary constraints on controls and control derivatives in accordance to the periodic soaring maneuver. (C) Considering the trigonometric series design, a free-final-time QP formulation including state, control, and control derivative constraints is derived, leading to a freecycle flight trajectory generation. An approximation of the wind strength variation is used in the QP form for online updating the trajectory in unspecified wind profiles.
This paper is structured to provide not only technical details but also insight about the proposed method: First,the problem formulation is given in Section 2. Next, the trigonometric series parameterization is detailed in Section 3,illustrating the mathematical properties and the utilization of them. After the development of the parameterization method,an offline comparison is presented in Section 4, showing the benefits and the corresponding trade-off of acquiring smooth control inputs. The online trajectory correction based on quadratic programming is then developed in Section 5,including the modeling of the wind strength variation and the formulation of the optimization problem. The simulation results of the online trajectory correction are presented in Section 6, the simulation scenario of which considers a randomly generated wind field. Finally, conclusions are drawn in Section 7.
2. Problem formulation


This constraint specifies that the cycle ends at a desired altitude with desired velocity direction,and yet the absolute value of the velocity can vary.On the other hand,an energy-neutral cycle additionally requires
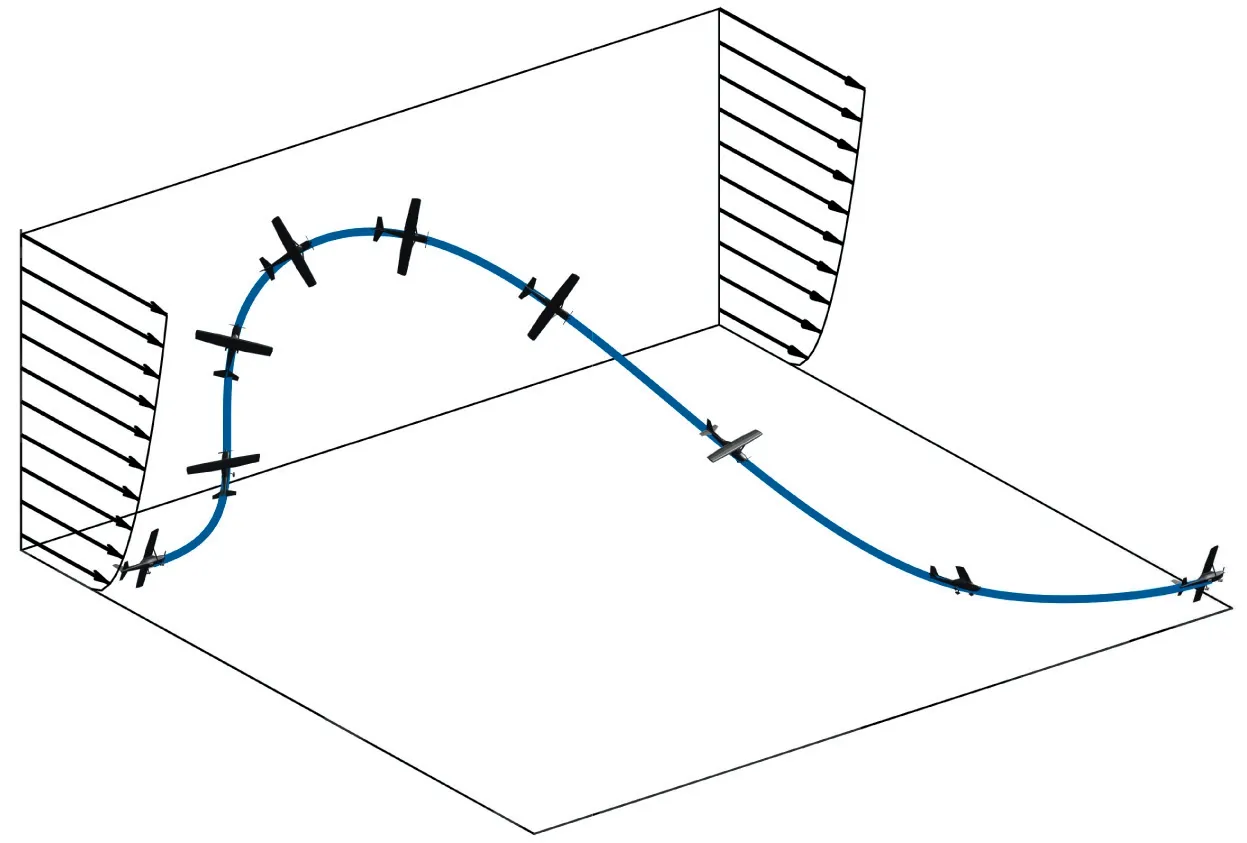
Fig.1 Schematic representation of a bend-type dynamic soaring cycle.18

The altitude should be higher than the minimum value,which is a state inequality constraint, as

3. Trigonometric series parameterization
In this paper,we apply a trigonometric series parameterization method,to formulate the control variables, where the series are infinitely differentiable. For aircraft/birds performing dynamic soaring, no discontinuities of any kinematic state or control physically exist in practice.Therefore,generated trajectories using the trigonometric series parameterization, which are guaranteed to be smooth,better represent the actual movement of aircraft/birds in the real-world. Moreover, a smooth trajectory may lead to a more efficient and robust usage of the control authority, as it avoids sacrificing control authority for following unphysical kinks and steps in the non-smooth optimal trajectory.
On the basis of Ref. 19, the periodicity of the series functions is designed to have the characteristic that can simplify the optimization problem. Moreover, as a free-cycle is required, the series are formulated with respect to the normalized time τ=t/t∊[0,1].The expression of the i-th variable of the control vector is given as:

It can be noticed that u and Shave a periodicity of 1,which automatically guarantees that the initial and terminal values of u and their derivatives are equal.

Also,u being a linear function of c leads that the incremental change of u and ˙u are linear to the increments of c.
4. Offline optimization
This section is dedicated to showing the difference of the minimum required wind strength for an energy-neutral cycle between using the Full Discretization (FD) and the Trigonometric Series (TS) parameterization. The model parameters and constraint values are given in Table 1. We use FALCON.m,which is a free-of-charge optimal control software,to generate comparison results, and the TS solution serves as the initial solution for the online simulation in the next section.The vehicle dynamics, i.e., the EoM in Eq. (1) are transcribed as equality constraints in the optimization problem. By default, FALCON.m utilizes a trapezoidal collocation for the discretization, where the control variables at each grid point are independent. After deploying the trigonometric series parameterization, the controls are functions of the coefficient vector, and a fifth order series is used. Before showing the numerical results,the two setups for the optimization problem formulation are summarized. For the original problem, we have

Next, the formulation with the trigonometric series parameterization is

One can notice that the differences in the two problem formulations are the unknown variables, the parameterization of controls, and the constraints on the control derivatives. The controls are the unknowns in Eq. (30), while in Eq. (31) the series coefficients are to be determined. The boundary and path constraints on control derivatives by Eqs. (21) and (22)are not considered in Eq. (30).
In the following, the offline optimization results are presented. The trajectories are shown in Fig. 2, and the time histories of the velocity components are displayed in Fig. 3. The time histories of controls and control derivatives are presented in Figs. 4 and 5, respectively. For analyzing the results, the behavior of the generated controls is examined first. It can be noticed in Fig. 4 that, although the boundary constraints on controls are satisfied, they lead to big undesired steps near the boundary points.This is because the controls are fully discretized in the FD scheme, and therefore they are mutually independent and are optimized independently. On the other hand, the controls are by construction smooth with the TS parameterization. Both Cand μchange smoothly. In the TS trajectory, the boundary constraints and the continuity of the lift coefficient lead to a larger utilization of its authority in the beginning and in the end.This results in larger turn rates and thus a smaller displacement in the ydirection, which can be seen in Fig.2.Also,as a result of the full discretization,the control derivatives are not continuous as shown in Fig. 5.However,the control derivatives generated by the TS parameterization are smooth. One additional benefit that can be noticed is that the bounds on the derivative are achieved by the TS method without introducing new variables, while they are not considered in the FD scheme.Moreover,the zero conditions at the boundary points are satisfied.The cycle times are 7∙31 s and 7∙40 s for FD and TS,respectively.The cycle time is marginally longer for the TS solution. The minimum required wind strength are 8∙12 m/s and 8∙49 m/s for FD and TS,respectively. There is a 4∙6% of suboptimality using the TS parameterization,whereas the smoothness of controls is significantly improved.
5. Online trajectory correction
This section summarizes the different approaches used for an online trajectory correction, consisting of wind strength variation(Section 5.1),reformulation of the dynamics(Section 5.2),and QP formulation (Section 5.3).
5.1. Wind strength variation
The philosophy of approximating the wind strength variation is to calculate the incremental change of a parameter in the wind profile model in Eq. (9).This approach is developed based on the assumption that the instant altitude and wind information is available. This assumption can be justified bythe recent progress in on-board wind estimation methods.Provided that hand Vare known, the reference wind strength Vcan be computed using Eq. (9), referred to as the nominal profile hereafter. The incremental change of Vbetween two consecutive time instances, i.e., the wind strength variation denoted by δV, can be thus calculated.The process is schematically shown in Fig. 6.The difference in Vbetween two red dashed lines is the approximated wind strength variation, δV. Moreover, it is important to note that we do not assume that the actual wind profile is in either the nominal shape nor any other certain shape.

Table 1 Model parameters and constraint values.
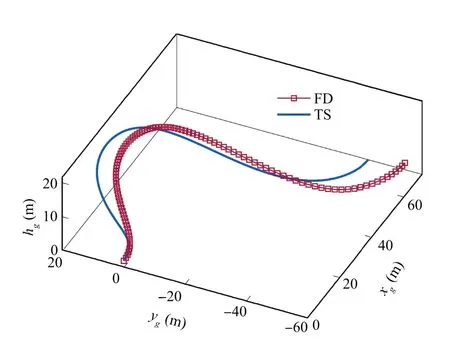
Fig. 2 Offline: Trajectories.
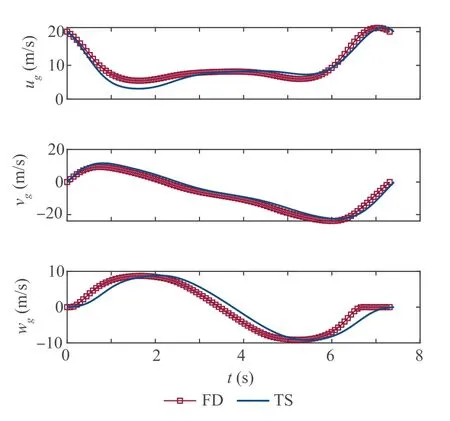
Fig. 3 Offline: Time histories of inertial velocity.
5.2. Reformulation and linearization of dynamics

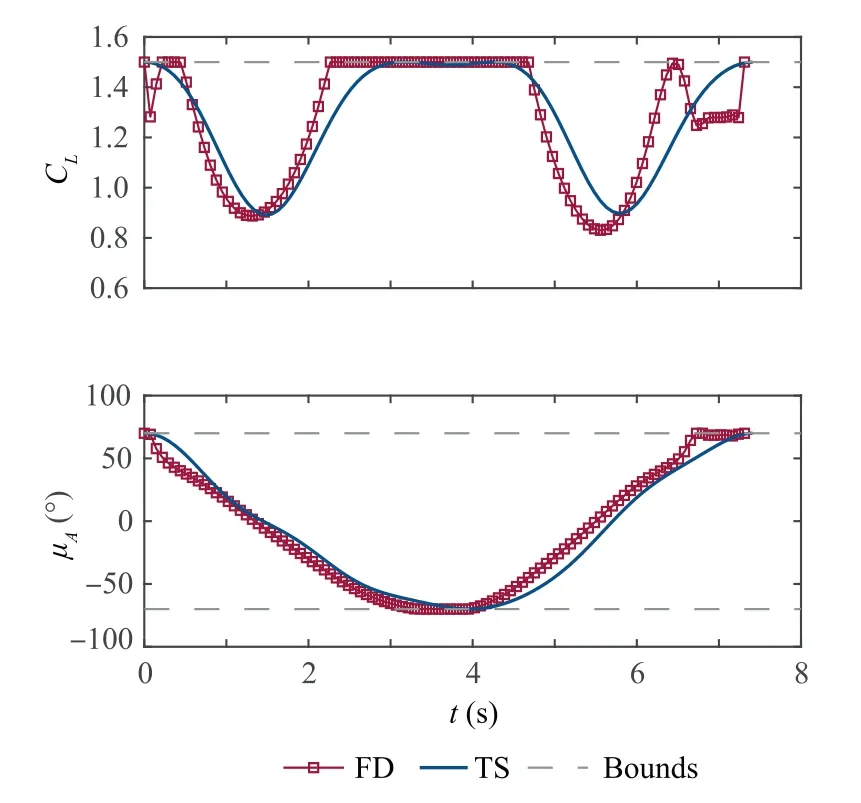
Fig. 4 Offline: Time histories of controls.
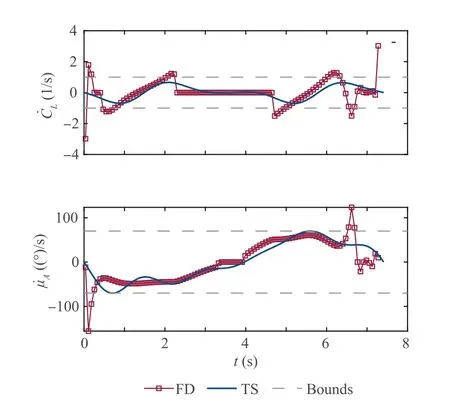
Fig. 5 Offline: Time histories of control derivatives.


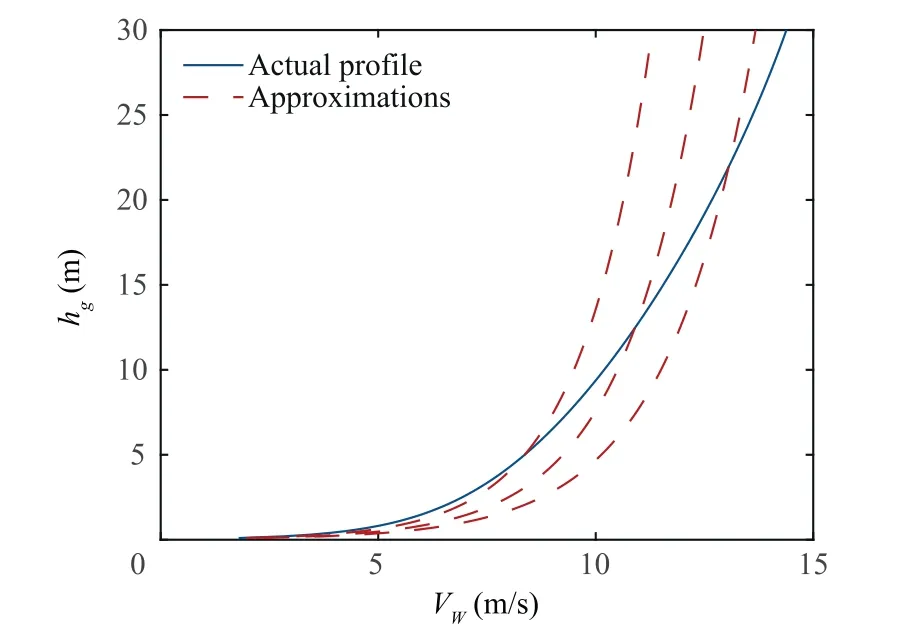
Fig. 6 Approximations of wind profile.18

Here, zfrom the left-hand side consists of all unknown increments that are used for correcting the flight trajectories.On the right-hand side, there are two terms, namely, v and e,representing the increments in states caused by the wind strength variation and the linearization errors, respectively.We assume that the wind strength variation between two consecutive steps is small, as the step itself is small. Therefore,dVis considered to be approximately equal to the wind strength variation obtained in Section 5.1 as

5.3. Quadratic programming formulation
The QP problem is formulated for correcting the flight trajectory online based on the initial solution, which is the energyneutral trajectory that has been shown in Section 4. The core objective is to determine the increment variables and update the cycle time and the associated controls for performing appropriate dynamic soaring in an unspecified wind profile.To do this, at first, the constraints in Section 2 are converted to expressions with respect to the unknown variables. After that,some constraints that facilitate the online implementation are given.


6. Numerical results of online trajectory correction
In this section, simulation studies are made for demonstrating the effectiveness of the proposed methods and results are presented. The simulation parameters are the same as in the previous Section 4. Time-varying wind profiles are generated for simulation purpose. We do not assume that the wind profile is always strong enough to support an energy-neutral dynamic soaring cycle.The used profiles may not coincide with the realworld patterns of the shear wind,but it is rational to verify the proposed method in randomly generated scenarios.
6.1. Single-cycle flight
This section presents the simulation results of a single cycle flight for a close observation of the flight.The actual wind profile is designed as
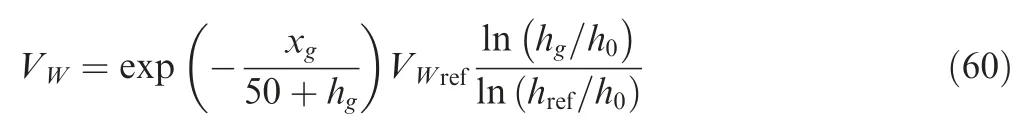
At x=0, the actual profile is equivalent to the minimumstrength nominal profile.Moreover,except the initial time,the profile is not of the nominal shape. The overall strength decreases as xincreases. The profiles are visualized in Fig. 7. The opaque surface is the actual wind profile, while the transparent surface represents the minimum-strength nominal profile, which also shows the actual flight trajectory and the initial trajectory. The actual flight trajectory deviates from the initial trajectory and is generally lower, which can be checked from the time histories of hshown in Fig. 8. Fig. 8 also displays the time histories of the inertial speed.The terminal speed are 19∙48 m/s and 20 m/s for the actual and initial trajectories, respectively. Therefore, the actual trajectory still makes good use of the wind energy to support the nonpowered flight, although the actual wind profile is not strong enough to support an energy-neutral cycle. Moreover, seen from the histories of the inertial velocity in Fig.9,the terminal velocity satisfies the terminal output constraints, as the terminal values of vand ware both zero. The cycle times for the actual and initial trajectories are 6∙91 s and 7∙41 s,respectively.A shorter cycle is generated online compared to the initial solution.The control histories are shown in Fig.10,and the histories of the control derivatives are embodied in Fig. 11. The boundary constraints are all met,facilitating good connections of cycles. The path constraints are satisfied as well. The continuity of control derivatives suggests that the smoothness of controls are retained in the online updating process. Solving a QP problem on a Windows platform with an i7-6700 and 16 GB of RAM using OSQP, which is a dedicated convex QP problem solver, in a Matlab environment takes no more than 0∙005 s, whereas the time step size is around 0∙07 s.
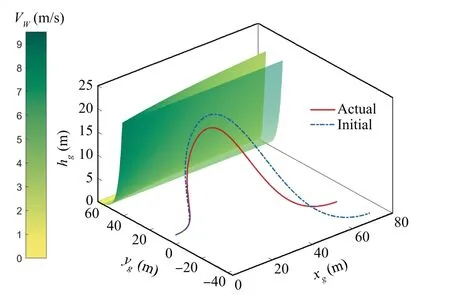
Fig. 7 Single-cycle: Trajectories and wind profiles.
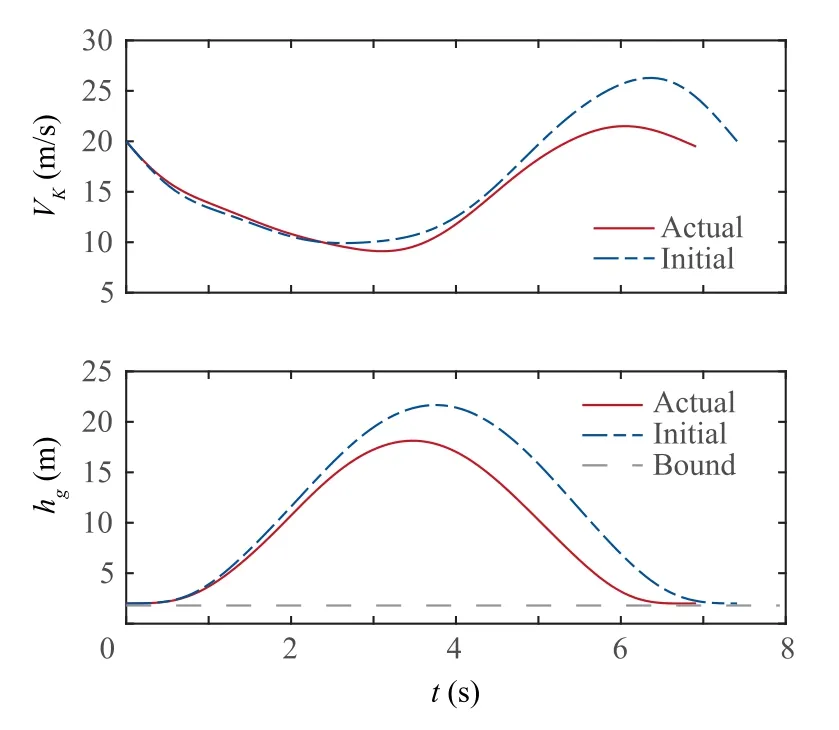
Fig. 8 Single-cycle: Time histories of speed and altitude.
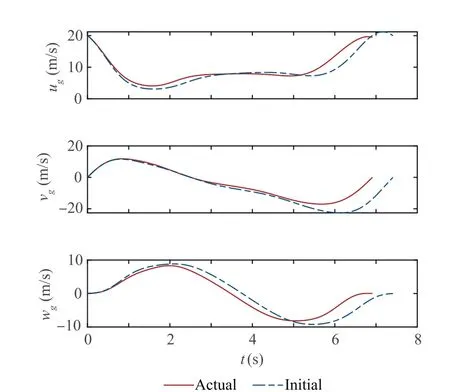
Fig. 9 Single-cycle: Time histories of inertial velocity.
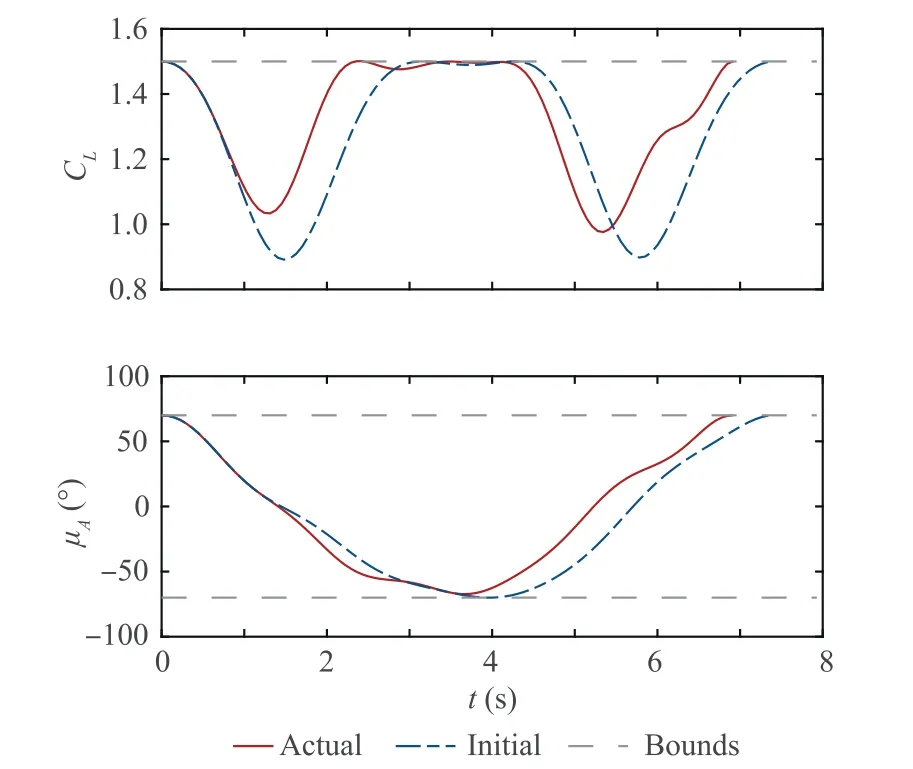
Fig. 10 Single-cycle: Time histories of controls.
6.2. Multiple-cycle flight
In this section, a simulation is carried out to verify the effectiveness of the proposed method in a multiple-cycle dynamic soaring flight. According to Ref. 21, when all measurements are used, an accurate wind estimation can be achieved. However, to demonstrate the effectiveness of the proposed method in a practical scenario in this section, we consider the wind measurement error as a normally distributed uncertainty(3σ=10%). The wind profile is expressed by
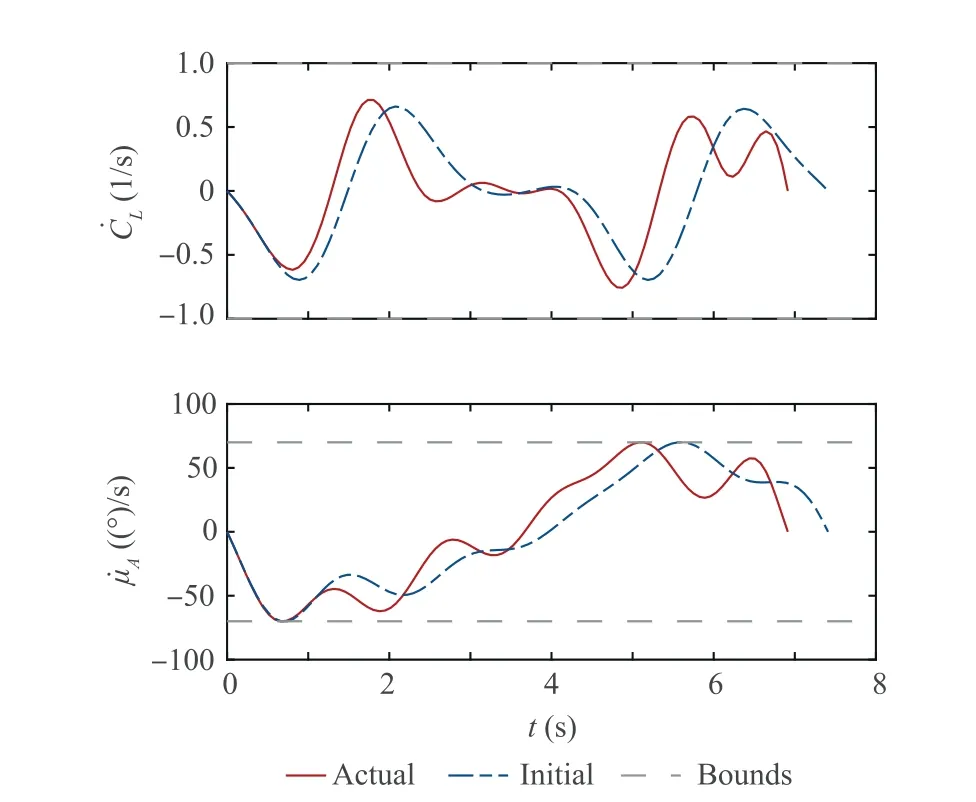
Fig. 11 Single-cycle: Time histories of control derivatives.
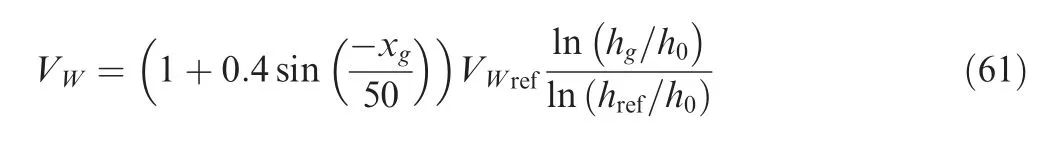
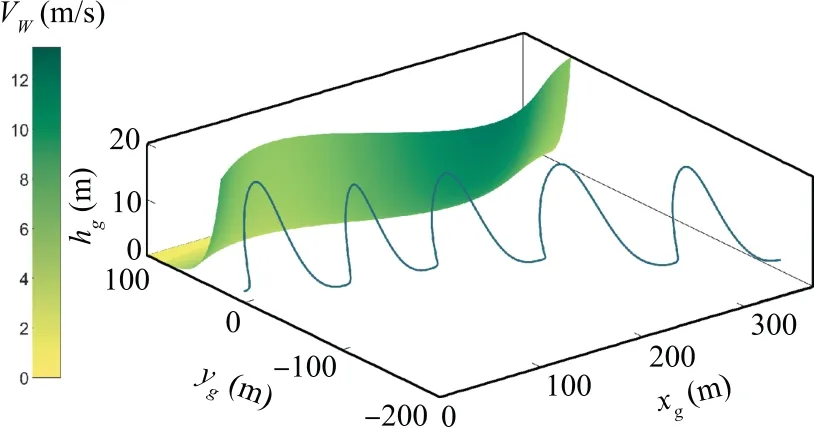
Fig. 12 Multi-cycle: Trajectory and wind profile.
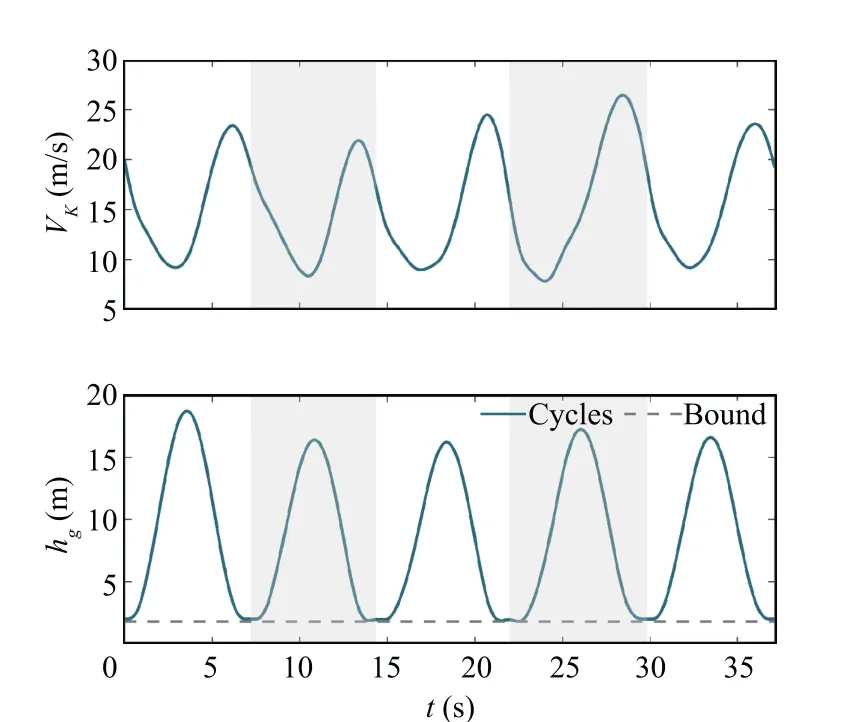
Fig. 13 Multi-cycle: Time histories of speed and altitude.
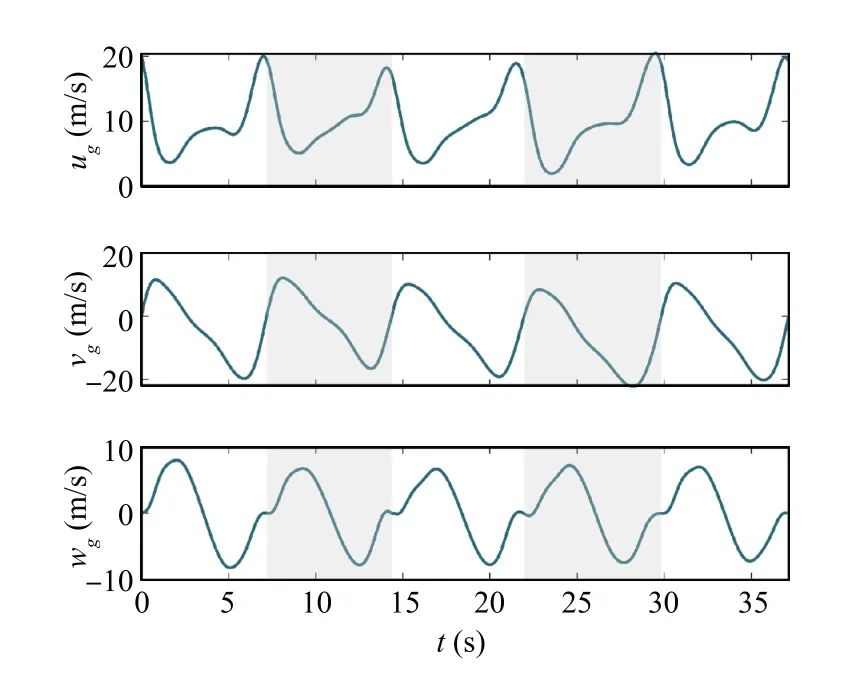
Fig. 14 Multi-cycle: Time histories of inertial velocity.
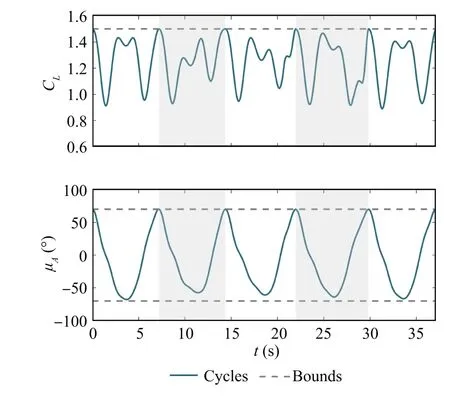
Fig. 15 Multi-cycle: Time histories of controls.
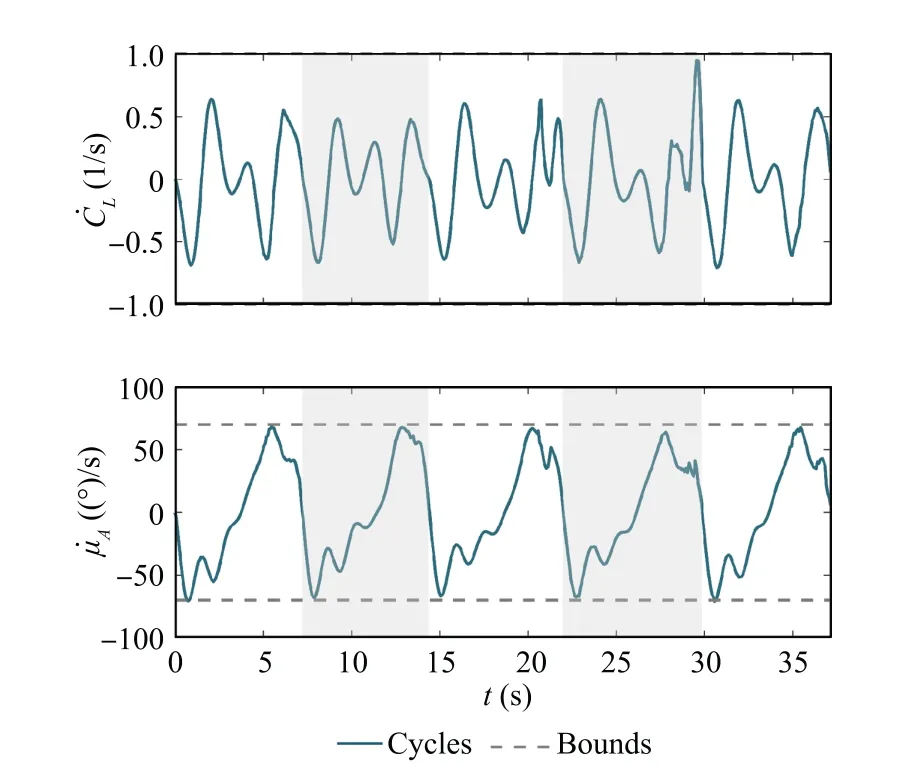
Fig. 16 Multi-cycle: Time histories of control derivatives.
and visualized in Fig. 12, in which the flight trajectory is also shown. Fig. 13 depicts the time histories of inertial speed and altitude.Cycles are distinguished by the background grids.The cycle times are 7∙19 s, 7∙18 s, 7∙59 s, 7∙87 s,and 7∙32 s.In combination with the wind profile seen in Fig. 12, one can notice that generally, a dynamic soaring cycle is shorter and has a smaller change in altitude when the wind is weaker and vice versa. The velocity components are embodied in Fig. 14, showing that the periodical dynamic soaring cycles are performed with slight differences due to the wind variation.The control histories, shown in Fig. 15, exhibit some differences among cycles. This is because the controls, especially the lift coefficients, need to be adjusted according to the wind strength variation,in order to make good use of the wind gradients.Finally,the time histories of the control derivatives are shown in Fig. 16. Control derivatives remain bounded. The oscillations are inevitable owing to the wind variation and the measurement errors. Consequently, the proposed method still performs well in the presence of wind measurement uncertainties.
7. Conclusions
This work investigated the smooth trajectory generation for dynamic soaring maneuvers. The introduction of the trigonometric series parameterization significantly enhances the smoothness of controls with a fair trade-off in terms of the minimum required wind strength for performing an energy-neutral cycle. The expression of the trigonometric series also by construction guarantees the connection of control inputs,simplifying the optimization formulation. The online optimizationbased strategy utilizes the wind strength variation approximated by the incremental change of a reference wind strength to correct the flight trajectory,featuring a free cycle time.The formulated quadratic programming problem can be very efficiently solved.The effectiveness of the proposed method is verified in scenarios where single and multiple dynamic soaring cycles are performed while the wind profiles are unspecified.
Future works include:(A)the study with more realistic wind field modeling, (B) the development and utilization of a six degrees-of-freedom dynamic model,(C)powered dynamic soaring, and (D) hardware-in-the-loop simulations. Furthermore,the control algorithm will be utilized in the scope of a research project on the application of dynamic soaring for UAVs.
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
This work was supported in part by the TUM University Foundation Fellowship and in part by the German Federal Ministry for Economic Affairs and Energy (BMWi) within the Federal Aeronautical Research Program LuFo VI-1 through Project ‘‘RAUDY” (No. 20E1910B).
 Chinese Journal of Aeronautics2022年7期
Chinese Journal of Aeronautics2022年7期
- Chinese Journal of Aeronautics的其它文章
- An online data driven actor-critic-disturbance guidance law for missile-target interception with input constraints
- Study on excitation force characteristics in a coupled shaker-structure system considering structure modes coupling
- Active and passive compliant force control of ultrasonic surface rolling process on a curved surface
- High dynamic output feedback robust control of hydraulic flight motion simulator using a novel cascaded extended state observer
- Composite impact vector control based on Apollo descent guidance
- Optimal trajectory design accounting for the stabilization of linear time-varying error dynamics
