High dynamic output feedback robust control of hydraulic flight motion simulator using a novel cascaded extended state observer

Wenxiang DENG, Jianyong YAO, Zongxia JIAO, Xiaohao LIU

a School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China

b the State Key Laboratory of Fluid Power and Mechatronic Systems, Zhejiang University, Hangzhou 310027, China

c School of Automation Science and Electrical Engineering, Beihang University, Beijing 100191, China

KEYWORDS Flight motion simulator;High dynamic tracking;Hydraulic actuator;Observer;Output feedback;Robust control

Abstract High dynamic tracking performance is a key technical index of hydraulic flight motion simulator (HFMS). However, the strong nonlinearities, various model uncertainties and measurement noise in hydraulic actuation systems limit the high dynamic performance improvement.In this paper, the outer axis frame of a HFMS is taken as a case study and its nonlinear dynamic model with consideration of strong nonlinearities, matched and mismatched uncertainties is established.A novel cascaded extended state observer (ESO) is proposed to estimate the unavailable system states to avoid the adverse effect of measurement noise on control performance. Meanwhile, the designed cascaded ESO also produces estimates of matched and mismatched uncertainties. Then,an output feedback robust controller (OFRC) is proposed by integrating the cascaded ESO with a robust integral of the sign of the error (RISE) feedback based on the backstepping framework.The proposed controller achieves compensation of both matched and mismatched model uncertainties in an output feedback form.Theoretical analysis indicates that the proposed OFRC ensures the boundedness of all closed-loop system signals in the presence of matched and mismatched timevarying model uncertainties.Excellent asymptotic tracking performance can also be obtained when the model uncertainties are time-invariant. Comparative experimental results show that the proposed OFRC achieves significant performance improvement compared with the extensively employed PI control with velocity feedforward (VFPI).

1. Introduction

Hydraulic flight motion simulator (HFMS) is a significant equipment in the comprehensive test and hardware-in-theloop simulation of guided weapons and aircrafts to verify the performance indices of sensors, inertial navigation systems and flight control systems.Though the merits of hydraulic actuation are apparent, i.e., small size-to-power ratios, high response capabilities, and large torques output, high performance tracking control of HFMS is challenging due to the existence of strong nonlinearities (e.g., nonlinear flow features of servovalve) and various model uncertainties (e.g., unmodeled friction effects and complex leakage characteristics).Moreover, the high dynamic tracking performance is particularly important for HFMSs due to the improving maneuverability demand of guided weapons and aircrafts. However,the influence of the system nonlinearities and model uncertainties on the tracking performance of hydraulic actuation systems is increasing with the increase of the tracking frequency.

During the past several decades,plenty of advanced nonlinear control methods have been developed to cope with the nonlinearities and model uncertainties for hydraulic actuation systems. A simple adaptive robust controlapproach was utilized to achieve friction compensation for a HFMS to reduce the main model uncertainty of the system.By integrating the robust integral of the sign of the error (RISE) feedbackwith adaptive backstepping control, Yao, et al. developed an adaptive RISE control algorithm for hydraulic actuation systems and excellent asymptotic tracking performance can be ensured.Won, et al. proposed a high-gain disturbance observer based controller with estimation of both matched and mismatched model uncertainties for electro-hydraulic systems.The adaptive control and disturbance observer were combined using backstepping method to handle parametric uncertainties and unmodeled disturbance, respectively.Neural network controland fuzzy controlwere also investigated for hydraulic actuation systems.

However, the abovementioned nonlinear control methods require full state information of hydraulic servo systems,which means not only the position but also velocity and pressure signals should be measured via sensors. On one hand, for practical hydraulic systems such as HFMS,only position sensors are usually installed considering the limitation of cost and spatial layout. On the other hand, even if the hydraulic systems are equipped with velocity and pressure sensors, heavy measurement noise are unavoidable and have significant impact on the control performance, especially the high dynamic performance.Therefore,output feedback control only using position feedback is always more suitable for practical hydraulic control applications and have received wide attention. Kim,et al. gave a high-gain state observer based output feedback control approach for electro-hydraulic systems to avoid the utilization of noise-contaminated velocity and pressure signals.However, the exact nonlinear model of the hydraulic system was required in the above high-gain observer based control design, which is often difficult to realize for practical systems. To this end, an extended state observer which can estimate the unmeasurable system states and model uncertainties was used in the backstepping control design, then noise alleviation and disturbance compensation were realized for hydraulic systems.It was subsequently extended to the output feedback model predictive control.In addition, Literatureemployed Levant’s differentiatorand unknown dynamics estimator to estimate the unavailable system states and unknown dynamics for hydraulic systems by transforming the original system model into a canonical form. It should be pointed out that these existing output feedback control schemes can only compensate for the matched model uncertainties. The practical hydraulic actuation system model usually has both matched uncertainties (e.g., complex leakage characteristics)and mismatched uncertainties(e.g.,unmodeled friction effects). Hence, output feedback tracking control of hydraulic actuators in HFMSs with compensation for both matched and mismatched uncertainties deserves to be further investigated.

In this paper, inspired from the traditional extended state observerdesign, a novel cascaded ESO which consists of two linear ESO is proposed to estimate the unmeasurable velocity and pressure signals, as well as the matched and mismatched model uncertainties of the hydraulic actuator of a HFMS. An output feedback controller is proposed by using the estimated system states and uncertainties obtained from the cascaded ESO based on backstepping framework. Moreover,in the proposed control design,a RISE feedback is incorporated to further improve the robustness of the hydraulic system against the model uncertainties. Lyapunov-based closed-loop system stability analysis shows that all system signals can be ensured to be bounded with the proposed control method in the presence of matched and mismatched timevarying model uncertainties, and asymptotic tracking performance is also guaranteed when the model uncertainties are time-invariant. Furthermore, owing to the nonlinear model based design and model uncertainties compensation, the proposed output feedback controller captures the main characteristics of the hydraulic actuation system and improved dynamic performance can be expected.The proposed control algorithm has been applied to the hydraulic actuator of a real HFMS and compared with the extensively employed VFPI control, and comparative experimental results have shown the high performance nature and superiority of the proposed control strategy.

2. System description and nonlinear model

2.1. System description

The five-axes hydraulic flight motion simulator under consideration is shown in Fig. 1. It consists of two parts: the carrier of the object(e.g.,the seeker installed on the head of a guided weapon to measure the moving parameters of a target relative to a guided weapon and produce guidance information)under test and the carrier of the target. The carrier of the object under test is configured with an orthogonal outer axis frame,a middle axis frame which is horizon to the outer axis,an inner axis frame, and a base, it is used to produce the kinematic physical effects of the object under test. The inner axis frame can achieve continuous roll and is driven by a high torque brushless AC motor fixed on the middle frame. The middle frame is driven by a servovalve-controlled hydraulic rotary actuator installed on one side of the outer frame and it can only realize limited pitch angular motion.The outer axis frame with limited yaw angular motion is also driven by a servovalvecontrolled hydraulic actuator located inside the base. In addition, the carrier of the target contains two axes, i.e., azimuth and pitch axes, which are both driven by servovalvecontrolled hydraulic actuators.These two axes are used to simulated the azimuth and pitch angular motion of the target.

Fig. 1 Five-axes hydraulic flight motion simulator.

Since the outer axis frame has large inertia characteristics,its high dynamic control is more challenging than the other axes.Hence,in this paper,the motion control of the hydraulic driven outer axis frame is taken as a case study with the other axes being fixed. The schematic diagram of the considered outer axis hydraulic servo system in HFMS is presented in Fig. 2. The hydraulic servo system in Fig. 2 is composed of a high-response servovalve,a hydraulic rotary actuator,the inertia load,an angular encoder and a motion controller.The principle of the hydraulic servo system can be described as follows.The calculation according to the designed control algorithm in the motion controller requires the desired motion trajectory and the actual position of the inertia load measured by the mounted angular encoder. The calculated control input voltage is applied to the servovalve to control the spool valve opening and then control the flowrate and pressure of the hydraulic rotary actuator.Finally,according to the torque balance equation, the position of the inertia load can be controlled. Therefore, the goal is to design a control algorithm to ensure that the position of the inertia load can well track the desired motion trajectory. Since no pressure sensors are installed,it limits the application of the existing full-state feedback control algorithms. To design a high dynamic tracking controller for the considered system, the establishment of its nonlinear model is first given as follows.

2.2. Nonlinear model of the outer axis frame

Applying Newton’s Second Law, the dynamics of the inertia load can be given by

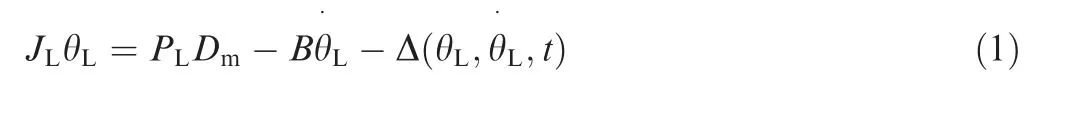
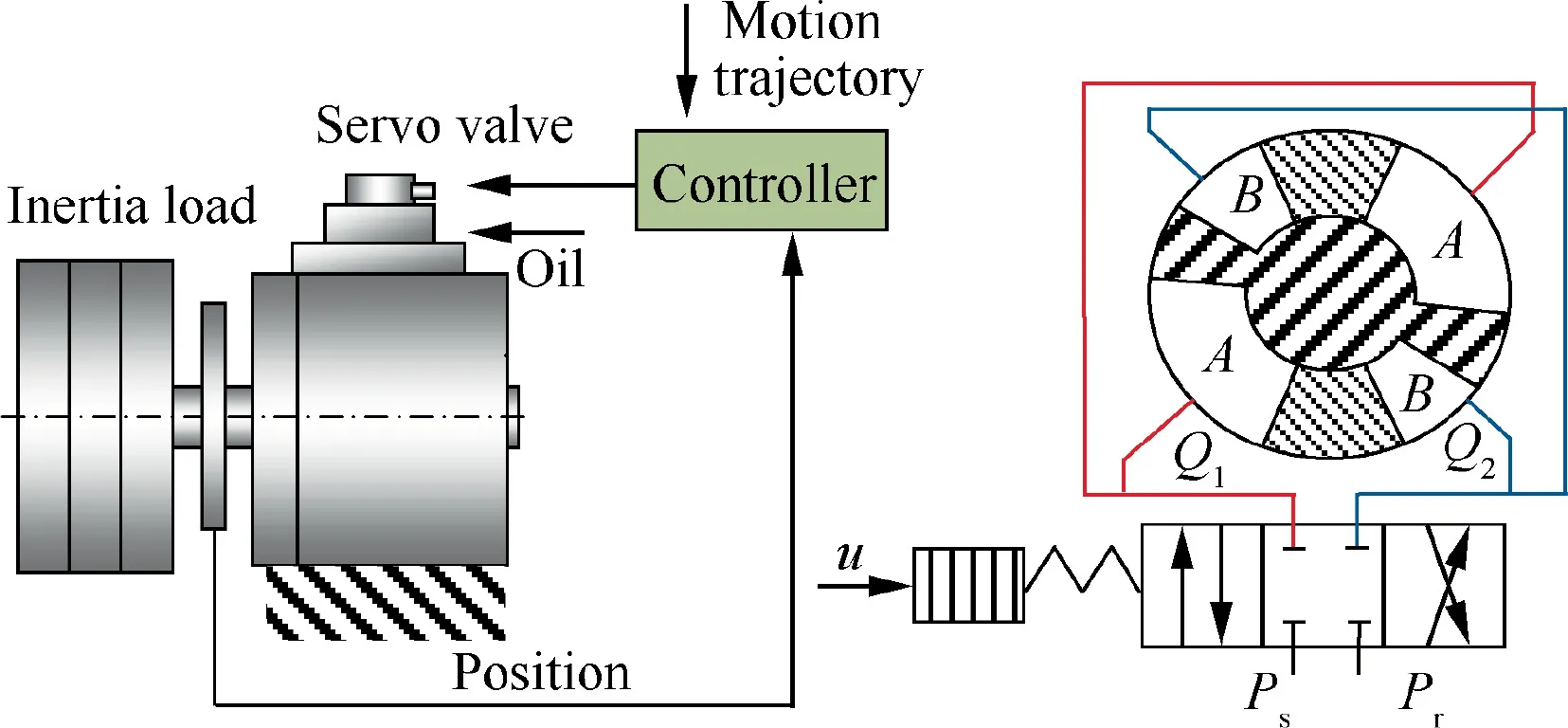
Fig. 2 Schematic diagram of considered outer axis hydraulic servo system in HMFS.

where Jdenotes the moment of inertia of load; θ,˙θ,¨θare the position,velocity,and acceleration,respectively;P=P–Pis the load pressure of the hydraulic actuator, in which Pand Pare the pressures inside the two chambers of the actuator; B is the viscous friction coefficient; Dstands for the radian displacement of the actuator, and Δ represents the lumped disturbance including unmodeled friction effects and external disturbance, etc.

The load pressure dynamics of the actuator is given by

where Cis the discharge coefficient, w is the spool valve area gradient,ρ is the density of oil,Pis the supply pressure of the fluid with respect to the return pressure P,xis the spool valve displacement, and the sign function is defined as

3. Output feedback robust controller design

3.1. Design model and issues to be addressed

Consider that only angular encoder is installed to obtain the position of the inertia load, some measures have to be taken to acquire the pressure signal of the actuator indirectly. In addition, as seen from Eq. (6) that the system model contains both mismatched uncertainty d(x, x, t) and matched uncertainty q(t).Note that traditional ESO can estimate the unmeasurable system states and model uncertainty simultaneously,however, the model uncertainty has to satisfy the matching condition. Therefore, it cannot be directly used to observe the matched and mismatched uncertainty in the hydraulic system. In this paper, a novel cascaded ESO is proposed to cope with this issue.

Before presenting the design procedures of the proposed cascaded ESO, we first extend the matched uncertainty q(t)and mismatched uncertainty d(x,x,t)as two additional states of the hydraulic system, i.e., define x=q(t)and x=d(x,x,t).In addition,let ξ(t)= ˙q, ξ(t)= ˙d and assume that both ξ(t) and ξ(t) are bounded. Hence, the original system model in Eq. (6) can be further written as follows:

3.2. Cascaded ESO design

3.3. Controller design

3.4. Main results and stability analysis

Lemma. Define the auxiliary function ψ(t) as

It can be obtained from(41)that W ∊Land V∊L.Since all signals are bounded,from Eqs.(10),(11),(18),(19),(27)and(28),itiseasytocheckthat ˙EisboundedandthefunctionEisuniformly continuous. By Barbalat’s Lemma, E →0 as t→∞,which completes the proof of result B of Theorem.

4. Experimental verification

In this section,comparative experiments are performed on the outer axis frame of a five-axis hydraulic flight motion simulator shown in Fig. 1. For the outer axis frame, the detailed parameters are listed in Table 1. The outer frame hydraulic servo system is controlled by the measurement and control system consist of the RTX real-time operating system and Labwindows/CVI. The sampling time is set as 0.5 ms.

The following two controllers are compared in the experiments.OFRC: This is the proposed output feedback robust controller with cascaded ESO in this paper.The control parameters are selected as:k=900,k=220,k=280,k=1,β=800,ω=15,ω=23.In addition,since the discontinuous sign function is contained in the final control input due to the differentiation on the virtual control law α,it is replaced with the following continuous function:where K, K, and Kare the P-gain, I-gain and velocity feedforward gain, respectively. The control gains are tuned via trail-and-error method, and they are selected as: K= 0.8 and K=0.01,and the gain K=0.085 V∙s/rad is determined based on the open loop identification.

Table 1 Key parameters of the outer frame hydraulic servo system.

To evaluate the performance of the compared controllers,the following performance indices are utilized, i.e., maximal tracking error M, average tracking error μ, and standard deviation of the tracking error σ, whose definition can be found in reference.

The two controllers are first tested by a normal level smooth sinusoidal motion trajectory x(t)= 10arctan(sinπt)-∙[1 - exp(-t)]/0.7854 deg. The comparative tracking performance of the compared two controllers is shown in Fig. 3 and the performance indices are listed in Table 2. As shown,the proposed OFRC achieves better tracking performance than the widely employed VFPI controller. The maximal output tracking error of OFRC is only about 60% of that of VFPI, and the other two performance indices of OFRC are also better than those of VFPI.In addition,the state estimates obtained from the cascaded ESO are presented in Figs. 4 and 5. It can be seen that the estimates of the position signal obtained by the third- and fourth-order ESOs are accurate,which indicates the accurate estimation of the unmeasurable states and model uncertainties according to the theoretical analysis. The control input of the proposed OFRC is given in Fig. 6, which is regular and bounded.

To test the high-dynamic tracking performance of the proposed control method, a sinusoidal motion trajectory with high frequency (5 Hz) is utilized, i.e., x(t) = 0.5arctan(si n10πt)∙[1 - exp(-t)]/0.7854 deg. The experimental results obtained for this case are presented in Table 3 and Fig.7.Since the proposed model-based OFRC controller considers the dynamic characteristics of the hydraulic servo system and compensate them in a feedforward way, it can be seen from the experimental results that the superiority of the proposed OFRC is more apparent than VFPI as the frequency increases.Hence, the proposed OFRC possesses better high-dynamic tracking performance. The state estimates obtained from the cascaded ESO and the control input are regular and are omitted for this case.

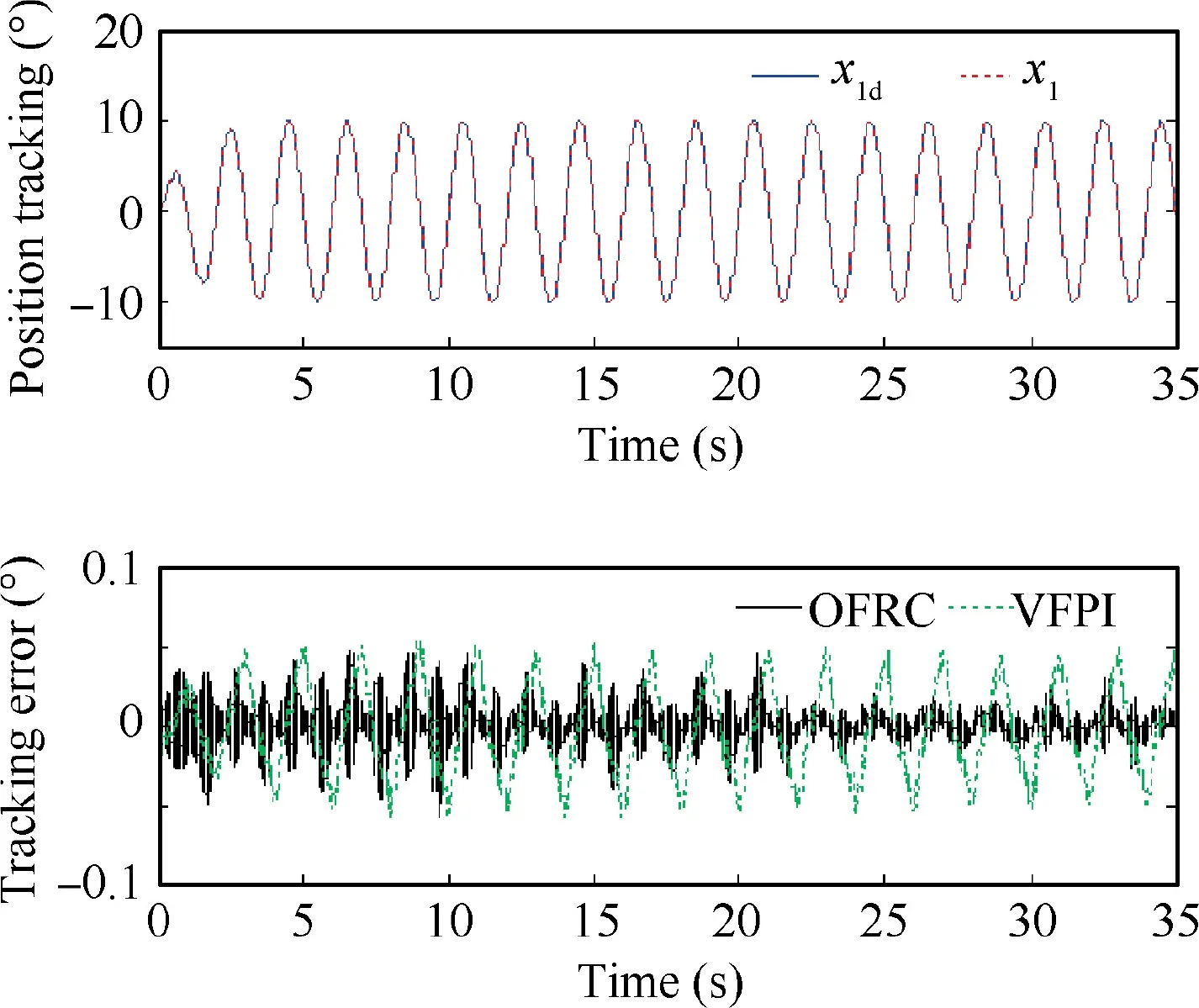
Fig. 3 Comparative tracking performance for 10 mm–0.5 Hz sinusoidal motion case.

Table 2 Performance indices during the last two cycles for 10 mm-0.5 Hz sinusoidal motion case.

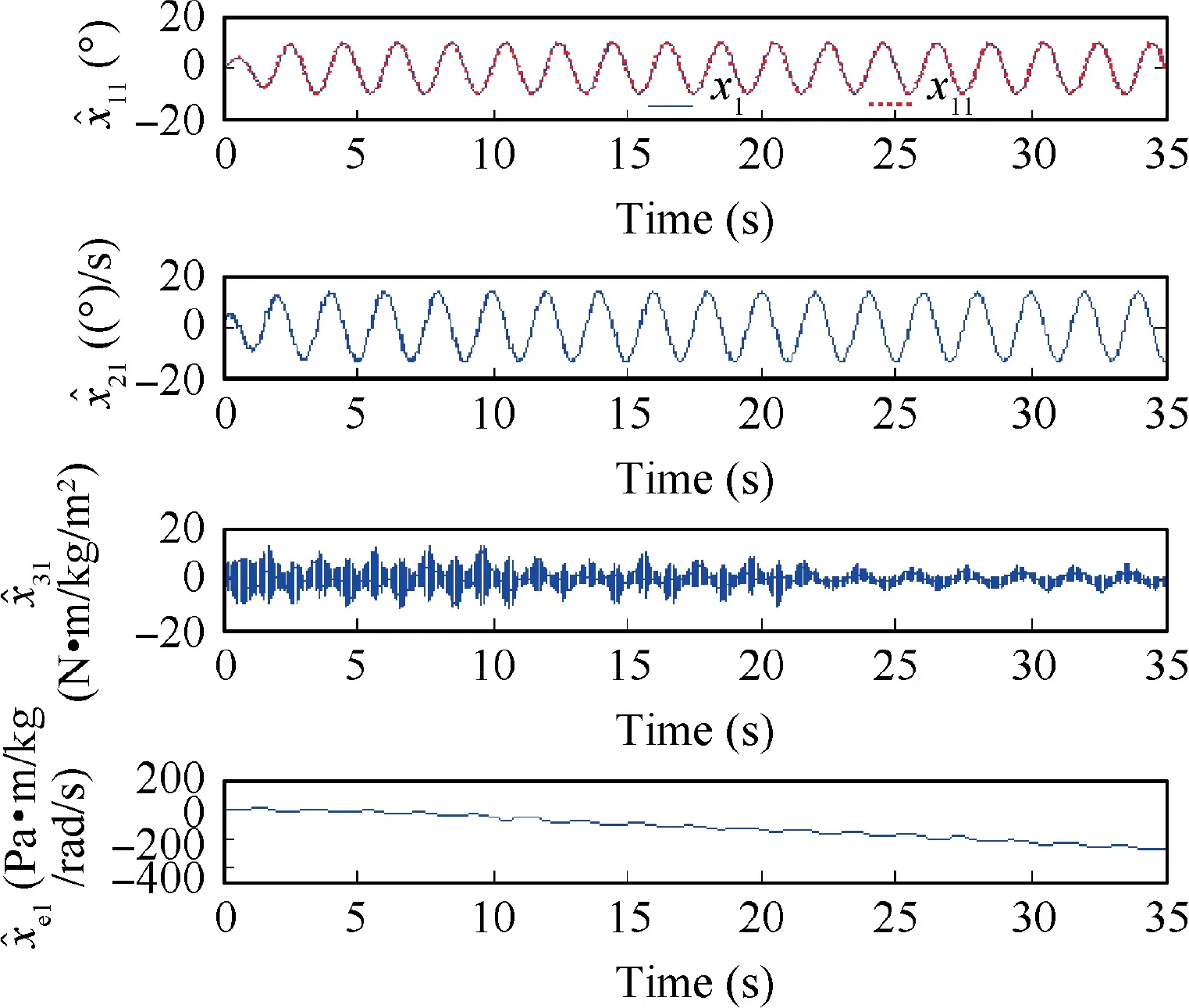
Fig. 4 State estimates obtained by the fourth-order ESO for 10 mm–0.5 Hz sinusoidal motion case.

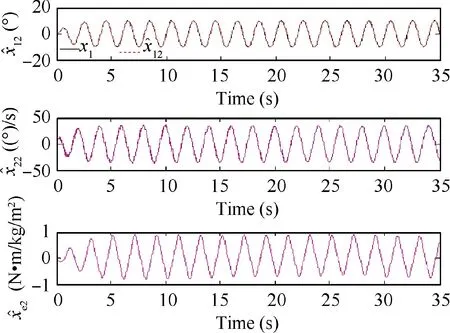
Fig. 5 State estimates obtained by the third-order ESO for 10 mm–0.5 Hz sinusoidal motion case.

In addition, a sinusoidal motion trajectory x(t) = 0.5arc tan(sin20πt)∙[1 - exp(-t)]/0.7854 deg with higher frequency(10 Hz) is utilized to further test the high-dynamic tracking performance.The performance indices and comparative tracking errors are shown in Table 4 and Fig. 8, respectively. As expected, the proposed OFRC still outperforms the VFPI in terms of all performance indices.

Fig. 6 Control input of OFRC for 10 mm–0.5 Hz sinusoidal motion case.

Table 3 Performance indices during the last cycle for 0.5 mm-5 Hz sinusoidal motion case.

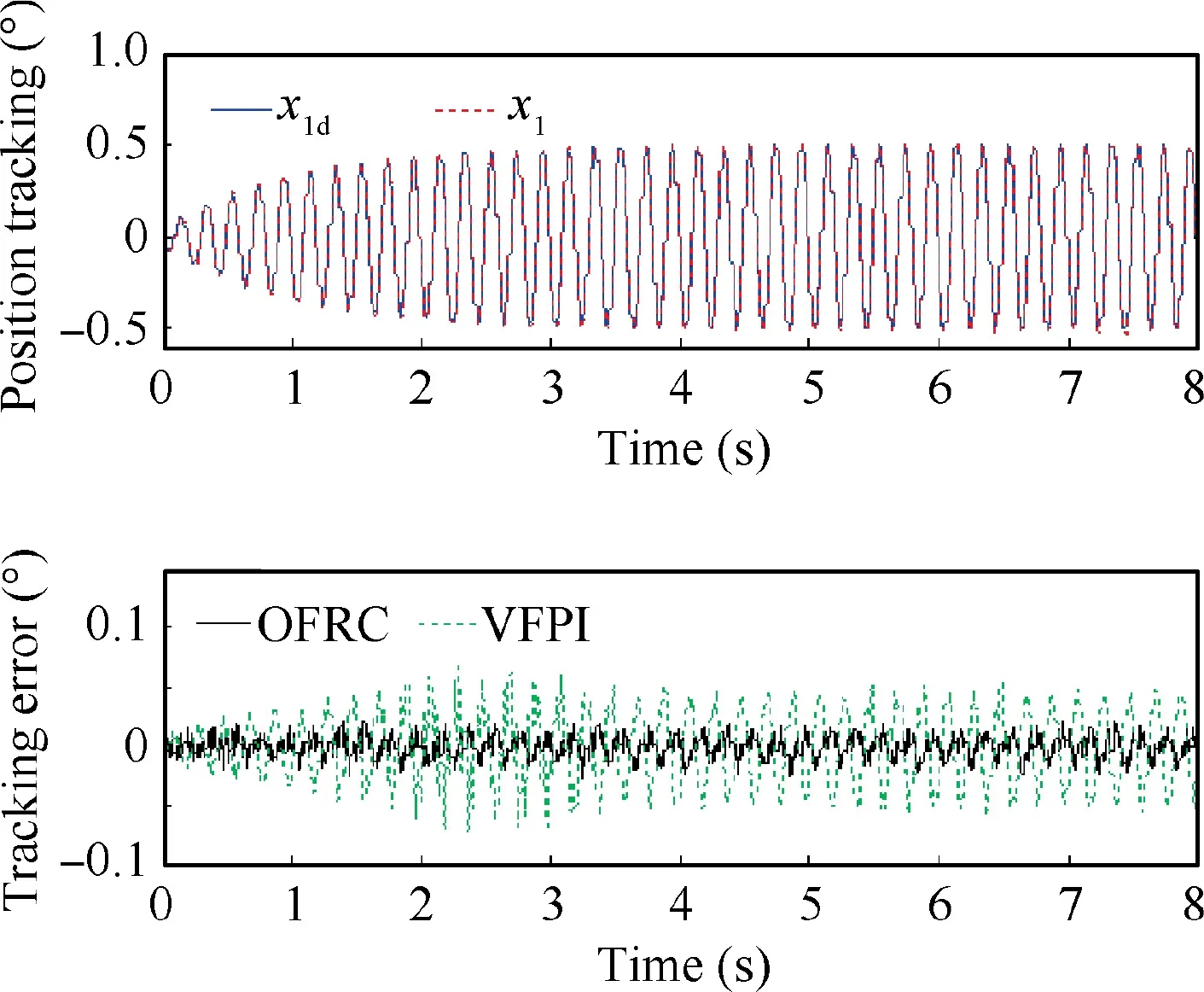
Fig. 7 Comparative tracking performance for 0.5 mm–5 Hz sinusoidal motion case.

Finally, the two controllers are tested by a series of sinusoidal motion trajectories whose frequency is from 1 Hz to 18 Hz to show the bandwidth expansion capability of the proposed control strategy. The Bode diagram with the two controllers are depicted in Fig. 9. As seen, the dynamic doubleten bandwidth (10% amplitude change and 10-degree phase lag), which is a more stringent performance index than the closed- loop bandwidth, is about 10 Hz with VFPI control and 15 Hz with the proposed OFRC. It means that the proposed OFRC effectively expands the double-ten bandwidth of the system owing to the nonlinear model-based feedforward compensation,disturbance compensation and noise alleviation with the cascaded ESO. Therefore, the proposed OFRC is more suitable and effective in practical applications requiring high-dynamic tracking performance with both high accuracy and high response.

Table 4 Performance indices during the last two cycles for 0.5 mm–10 Hz sinusoidal motion case.

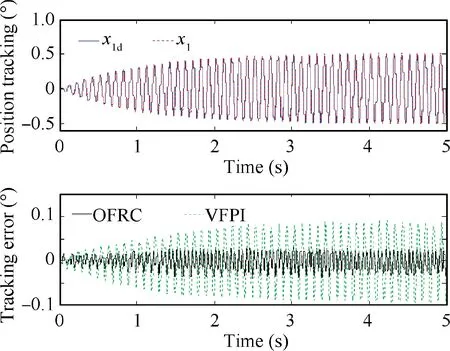
Fig. 8 Comparative tracking performance for 0.5 mm–10 Hz sinusoidal motion case.

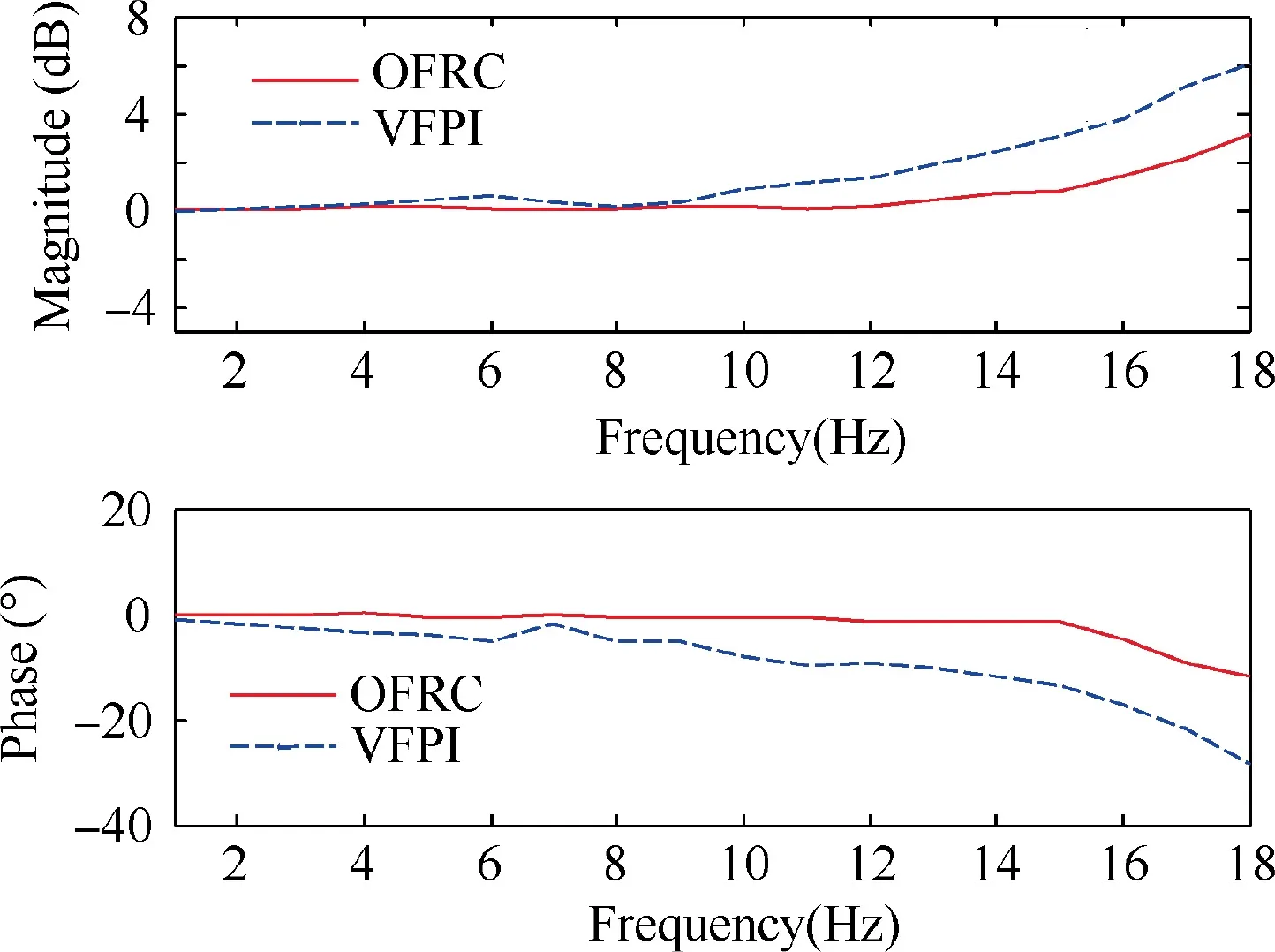
Fig. 9 Bode diagram with two controllers.

5. Conclusions

In this paper, the high dynamic tracking control of the outer axis frame of a HFMS is studied. Since only the position sensor is installed, a novel cascaded ESO is proposed to achieve estimation of the unavailable velocity and pressure signals for output feedback control design.Meanwhile,the estimation of both matched and mismatched model uncertainties can also be obtained by the proposed cascaded ESO.Therefore,an output feedback robust controller is synthesized by combining the cascaded ESO with a continuous RISE feedback term via the backstepping method. Due to the nonlinear model-based output feedback control design, the adverse effects of model uncertainties and measurement noise are significantly attenuated with the proposed controller and high dynamic tracking performance can be expected. The close-loop system stability analysis indicates that the proposed controller guarantees all the system signals to be bounded if the model uncertainties are time-varying and obtains excellent asymptotic tracking performance in the presence of time-invariant model uncertainties. Comparative experimental results show that the proposed OFRC achieves better tracking performance than VFPI controller in terms of all performance indices.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This work was supported in part by the National Natural Science Foundation of China under Grant 51905271 and Grant 52075262, in part by the Natural Science Foundation of Jiangsu Province under Grant BK20190459, in part by the Fundamental Research Funds for the Central Universities under Grant 30920041101, and in part by the Open Foundation of the State Key Laboratory of Fluid Power and Mechatronic Systems under Grant GZKF-201910.