Time-optimal guidance for intercepting moving targets with impact-angle constraints

Yun ZHENG, Zheng CHEN,b,*, Xueming SHAO,b, Wenjie ZHAO

a School of Aeronautics and Astronautics, Zhejiang University, Hangzhou 310027, China

b State Key Laboratory of Fluid Power and Mechatronic Systems, Zhejiang University, Hangzhou 310027, China

KEYWORDS Dubins vehicle;Guidance law;Minimum-time path;Optimal guidance;Path planning

Abstract The minimum-time path for intercepting a moving target with a prescribed impact angle is studied in the paper.The candidate paths from Pontryagin’s maximum principle are synthesized,so that each candidate is related to a zero of a real-valued function.It is found that the real-valued functions or their first-order derivatives can be converted to polynomials of at most fourth degree.As a result,each candidate path can be computed within a constant time by embedding a standard polynomial solver into the typical bisection method. The control strategy along the shortest candidate eventually gives rise to the time-optimal guidance law.Finally, the developments of the paper are illustrated and verified by three numerical examples.

1. Introduction

In this paper, we consider a 2-dimensional pursuer-target engagement. The pursuer moves forward at a constant speed with a minimum turning radius,and the target moves at a constant speed. Such an engagement is probably one of the most popular problems in the field of endgame guidance.In practical scenarios, minimizing the engagement duration is crucial for the pursuer to successfully intercept the target, as it is essential to reduce the probability of detection and to improve survivability against countermeasures.For this reason, the Time-Optimal Guidance Problem (TOGP) for a pursuer to intercept a target has been widely studied in the literature.

It should be noted that the previously described pursuer takes the same kinematic model as the Dubins vehicle.Therefore,when the target is stationary and the final impact angle is not constrained, the TOGP is degenerate to the well-known Relaxed Dubins Problem (RDP).The solution path of RDP has been proven in Ref. 7 to be in a sufficiently family of four candidates. If the final impact angle is fixed, it is known according to Ref. 6 that the time-optimal path can be computed within a constant time by checking at most six candidate paths.Further study along this direction of research considers controlling both final impact time and final impact angle.

In all the aforementioned papers,the targets are considered stationary. From a practical point of view, it is important to consider that the target is moving. Without constraints on the final impact angle, Meyer et al. 9 established some sufficient conditions to ensure that the time-optimal path for intercepting a moving target shared the same geometric pattern as the path of RDP. Whereas, there was a gap between necessary and sufficient conditions, and it was not clear how to devise the time-optimal guidance law if the sufficient conditions were not met. More recently, the minimum-time paths for intercepting moving targets were thoroughly synthesized in Ref. 10, which allowed developing an efficient and robust algorithm to compute the corresponding time-optimal guidance law for intercepting moving targets.

However,the final heading angle is left free in Refs.9,10.A specific terminal heading is essential for various pursuer-target engagements.For example,a pursuer with a directed warhead,against ground and ocean targets, is more effective when the impact occurs at a certain angle.For this reason, the study on optimal guidance with impact-angle constraints is quite active in the field of endgame guidance. The TOGP for intercepting moving targets with lateral impact angle was first studied in Ref.11;it was found that the time-optimal guidance law was actually determined by a zero of a highly nonlinear equation. A natural extension was presented in Ref. 5 where the final impact angle could be assigned to any value.To be specific,by a coordinate transformation,the authors of Ref.5 managed to convert the TOGP with a general constraint on impact angle to the special problem in Ref.11.As a result,the method presented in Ref. 11 was used to find the time-optimal fixedimpact-angle guidance law by finding a zero of nonlinear equations.In addition to Refs.5,9–11,the TOGP has been studied in an alternative way as it is equivalent to the problem of planning minimum-time path in a constant drift field.Without constraints on the final heading angle, the minimum-time paths in a constant drift field were related to zeros of some nonlinear equations,and the typical Newton iterative methods and bisection method were proposed to find the minimum-time paths in Refs. 13–15.

It is worth noting that a nonlinear equation may have multiple zeros, but only a specific zero is related to the timeoptimal fixed-impact-angle guidance law. Thus, the typical Newton-like iterative method and bisection method proposed in Refs.5,11,13,14 are not robust to find the optimal guidance law. The reasons include that (A) the numerical methods may not be able to converge to a zero if the initial guess is not appropriately chosen, and (B) even if the numerical methods converge to a zero, it is not necessarily the desired one related to the optimal guidance law,as shown by the numerical examples in Section 5.

In order to be able to compute the time-optimal fixedimpact-angle guidance law in a robust and efficient way, the TOGP is revisited in this paper. First of all, the solution path of the TOGP for intercepting a moving target with impactangle constraints is synthesized and some geometric properties are presented. Using these geometric properties, some nonlinear equations in terms of the solution path’s parameters are formulated. These nonlinear equations or their derivatives can be transformed to some polynomials of at most 4th degree.As a consequence, simply embedding a standard polynomial solver into the bisection method leads to a robust and efficient method for finding the time-optimal fixed-impact-angle guidance law. Since the problem of planning the shortest path in a constant drift field can be converted to the TOGP with a moving target,it follows that the developments of this paper also allow efficiently planning shortest paths in a constant drift field.

This paper is organized as follows.In Section 2,the TOGP for intercepting moving targets is formulated. Necessary conditions for optimality are established and transcendental equations in terms of the solution path’s parameters are formulated in Section 3. In Section 4, a numerical method is presented so that the time-optimal fixed-impact-angle guidance law can be computed within a constant time.Numerical examples are presented in Section 5,verifying and illustrating the developments of this paper.

2. Problem formulation

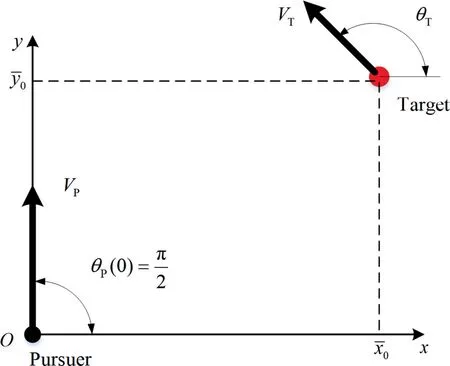
Fig. 1 Geometry and coordinates system.

3. Characterizing solution of the OCP

It has been proven in Ref.6 that,if the distance between the initial and final positions of the pursuer is at least 4ρ,the solution of the OCP is a circular arc, followed by a straight line segment, and followed by another circular arc. In this paper,the separation between the initial and final positions is also assumed to be at least 4ρ,as was done in the seminal works.Then, the geometric pattern of the OCP’s solution can be denoted by CSC, where ‘‘C” and ‘‘S” represent a circular arc with radius of ρ and a straight line segment, respectively. If a circular arc C has a right (resp. left) turning direction, we represent it by R (resp. L). Then, we have that the CSC type includes four different types, i.e.,

The proof of this theorem is postponed to Appendix B. In the next section, the results in Theorem 1 will be used to find the solution of the OCP.

4. Numerical method for finding the optimal control

Fig. 2 Geometry for the paths of CαSβdCγ. (cl0,cr0,clf and crf are defined in Appendix A.).

As presented in Appendix A,it suffices to compute the value of β in order to devise the optimal control strategy.According to Theorem 1, if the solution path is of type RSR or LSL, the value of β can be obtained analytically by finding the zeros of Eqs.(9)and(10),respectively.However,the transcendental equations Eqs.(11)and(12)may have multiple zeros but only a specific zero is related to the optimal path. Existing numerical solvers cannot be guaranteed to find the desired zero related to the optimal path, as illustrated by the numerical examples in Section 5. In the remainder of this section, a robust and efficient method will be presented to find all the zeros of equations having the same form as Eqs. (11) and(12).As a result,the optimal path of the OCP can be computed robustly and efficiently by ruling out useless zeros.

Let us define a function

Algorithm 1. Finding all the zeros of G1 (β )Step 1. Set i=0 and Z=∅.Step 2. If i ≤n, go to Step 3; otherwise, go to Step 4.Step 3. If G1 (βi )=0 Z=Z ∪ ｛βi ｝Elseif G1 (βi )×G βi+1( )<0 z=B G1 (β ),βi,βi+1■■Z=Z ∪ ｛z ｝Endif Set i=i+1 and go to Step 2.Step 4. End

5. Numerical examples

In this section, some numerical examples were simulated to demonstrate the developments of this paper. Before proceeding, it is worth mentioning that a large number of the examples were tested on a desktop with AMD Ryzen 2500U, showing that the time-optimal fixed-impact-angle guidance law for any example could be established within 10s.

For numerical convenience,the position was normalized so that the speed of pursuer was one, i.e., V=1 m/s.

5.1. Case A: Time-optimal guidance for intercepting a moving target

In order to find the time-optimal path for case A, one needs to check the lengths of all the four candidate paths in CSC, and the shortest candidate gives rise to the solution path. Regarding the candidate path of RSR, it was found analytically that Eq. (9) had two real zeros. Considering the fact that the two zeros represent the orientation angle of straight line segment, we can use a simple geometric analysis to rule out one useless zero, and another zero can be used to compute the length of path of RSR. For this example, the length of the candidate path of RSR was obtained as 16.63 m. Analogously, by analytically finding the zeros of Eq. (10), the length of the path of LSL was obtained as 9.58 m. When computing the lengths of the paths of RSL and LSR, Algorithm 1 was used to find all the zeros of Eqs. (11) and (12). Numerical results indicated that both Eqs. (11) and (12) had 2 real zeros. By geometric analysis, useless zeros were ruled out and the lengths of the paths of RSL and LSR were obtained as 10.16 m and 9.49 m, respectively. Therefore, it is concluded that the shortest path for case A is of type LSR. The shortest path is presented in Fig. 3(a), and the corresponding optimal control strategy is presented in Fig. 3(b). The last circular subarc exists but it is quite short, as shown by the scaled plot in Fig. 3(b).

Analogous to the present paper,it was proposed in Ref.11 to find the optimal path of this example by finding zeros of a nonlinear function F(x) where xis the projection of the final position on x axis. The value of the nonlinear function F(x)against xis plotted in Fig. 4, showing that it is discontinuous and has more than one zero.

Only is a specific zero related to the optimal path, but existing numerical solvers do not necessarily converge to the desired zero. Once the second zero in Fig. 4 is found,it leads to a non-optimal path (the length is 16.56 m), as presented in Fig. 5. In order to show that the developed method can find the optimal paths with any constraint on the final impact angle, the optimal paths with the final impact angles being π/4,3π/4,5π/4, and 7π/4 are computed,as presented in Fig. 6.

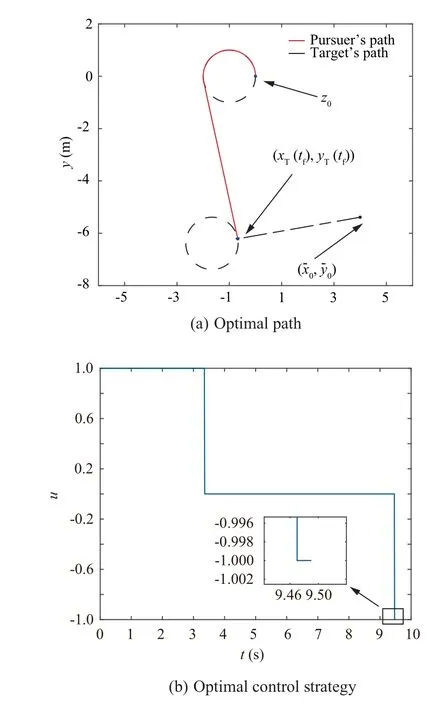
Fig.3 Solution path and corresponding optimal control strategy of the OCP (Case A).

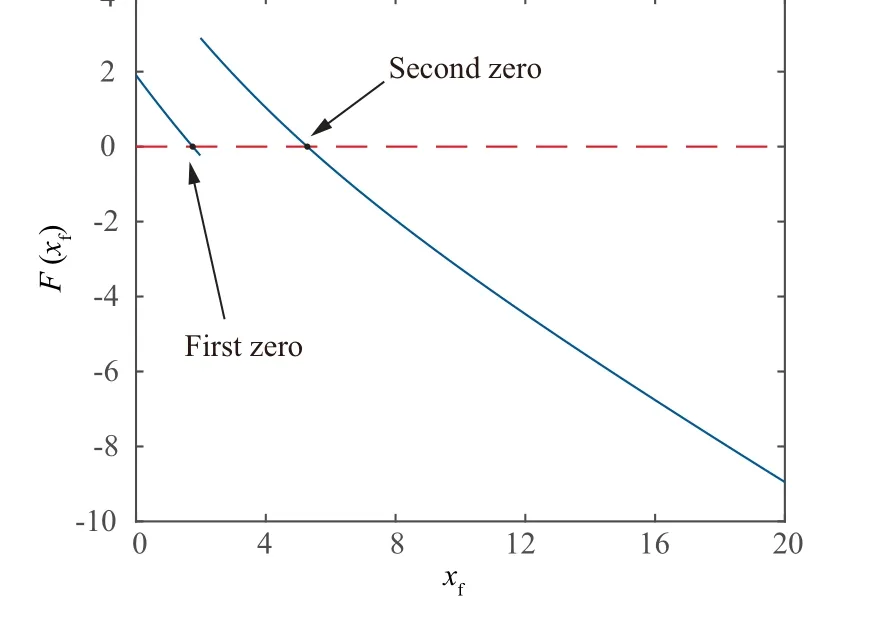
Fig. 4 F(xf ) related path type of RSL in Ref. 11 (Case A).

5.2. Case B: Path planning in constant drift field

The motions of aerial vehicles and underwater vehicles are usually affected by wind and ocean current,respectively.Thus,it is of practical importance to plan the shortest path in a constant drift field.

Fig. 5 Non-optimal path related to the second zero of F(xf ) in Ref. 11 (Case A).

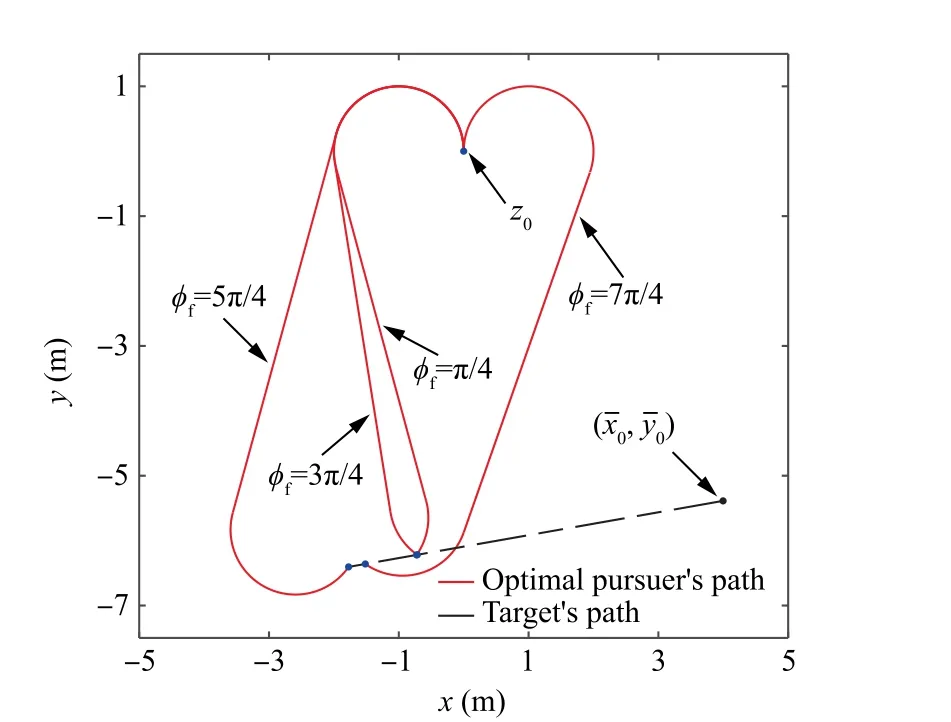
Fig.6 Optimal paths with different final impact angles(Case A).

By a simple coordinate transformation,this path planning problem in a constant drift field can be equivalent to the TOGP with a moving target, and the velocity of the moving target is equivalent to -w. According to the numerical procedure in Section 4, by finding zeros of nonlinear equations in Eqs. (9)–(12), the solution path of the TOGP was obtained as of type LSR,presented in Fig.7(a).Then,the reverse coordinate transformation in Refs.10,12 was used,leading the path of LSR into the shortest path in constant drift field,presented in Fig.7(b).The optimal control strategy is reported in Fig.8.By the same procedure, the optimal paths with different final impact angles in the drift field are computed and presented in Fig. 9, showing that, even if the motion of the pursuer is affected by a drift, the developed method can be used to find the optimal paths with any final impact-angle constraints. It is seen from Figs.7(b)and 9(b)that the solution paths in constant drift field are not the concatenation of circular arcs and straight line segments anymore,which coincides with the result in Ref. 15.

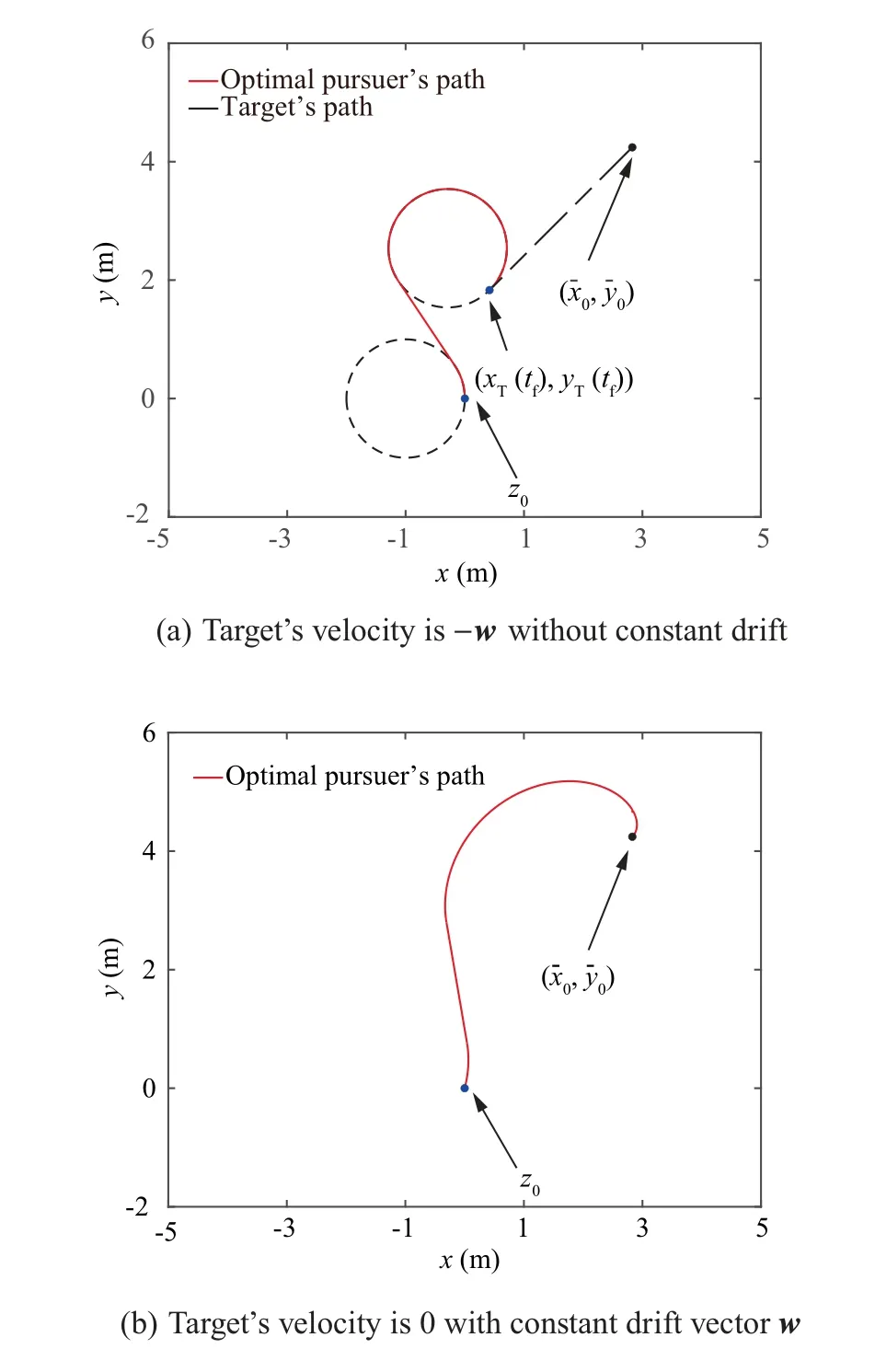
Fig. 7 Solution path of the OCP and corresponding path in constant drift (Case B).

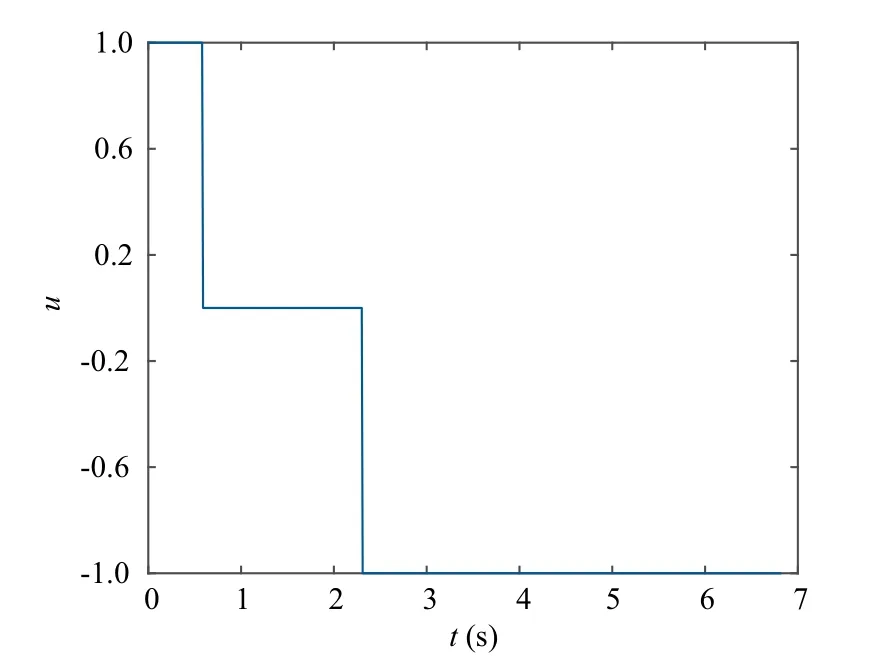
Fig. 8 Optimal control strategy against time (Case B).

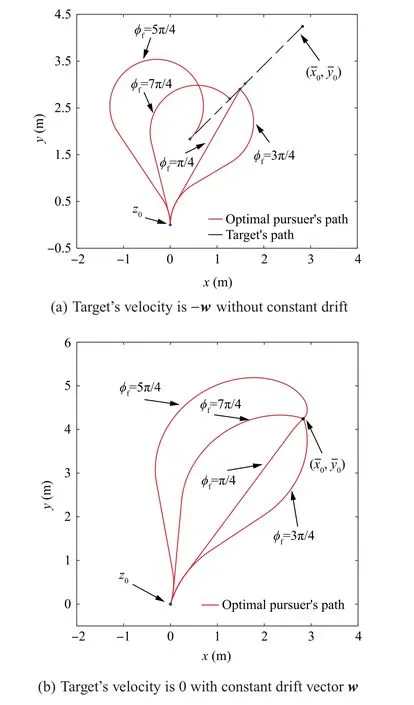
Fig. 9 Solution paths with different final impact angles and corresponding paths in constant drift (Case B).

5.3. Case C: Time-optimal guidance with a moving target in constant drift field

To the authors’ best knowledge, this problem has not been addressed in the literature. By the coordinate transformation in Refs. 10,12, this problem is equivalent to the TOGP for intercepting a moving target with velocity of -w+v. As a result, we are able to employ the numerical procedure in Section 4 to find the solution of the TOGP, presented in Fig. 10(a). By the reverse of the coordinate transformation,we immediately have the time-optimal path of the original guidance problem in constant drift of w, presented in Fig. 10(b).The optimal control strategy is reported in Fig. 11.

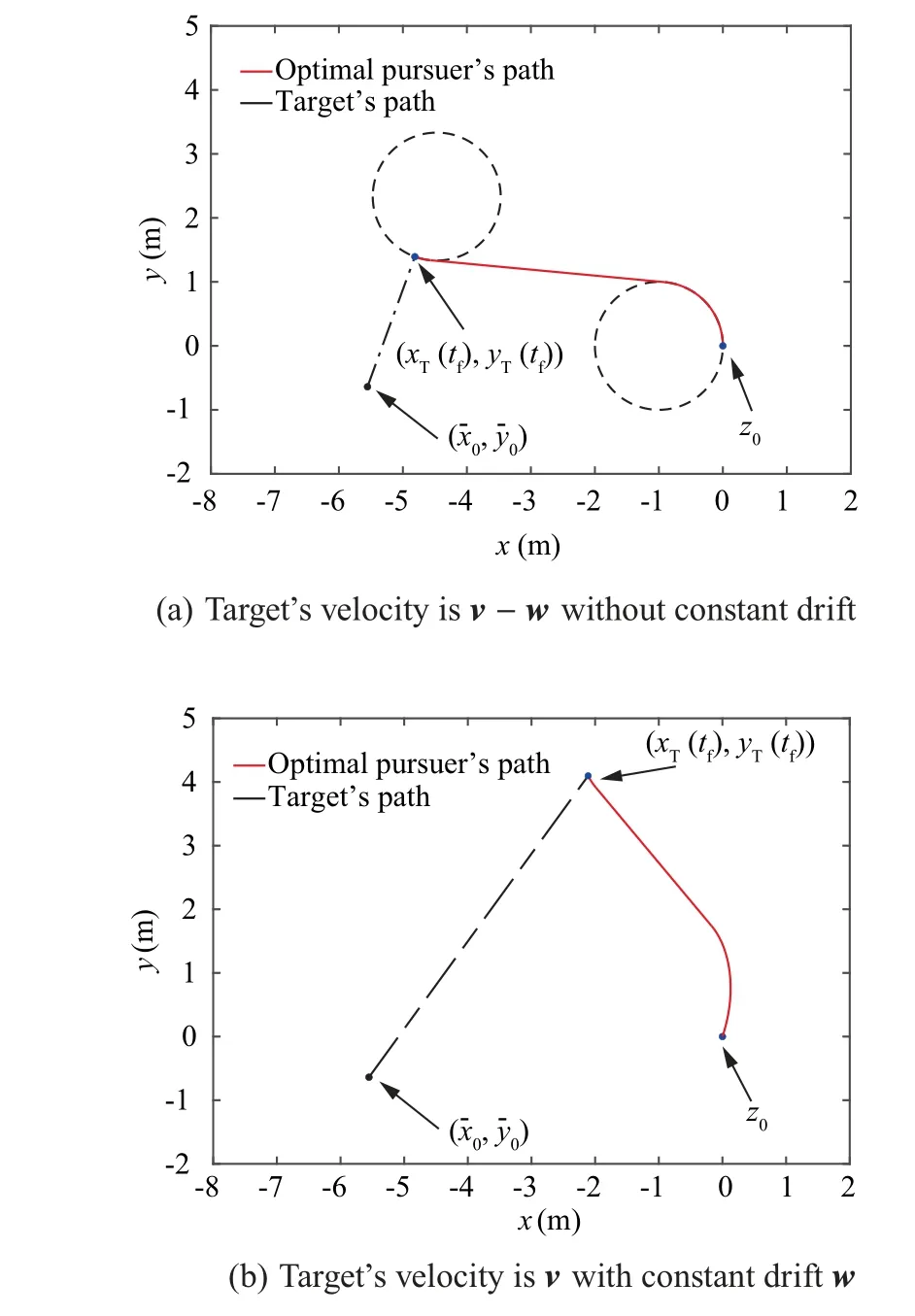
Fig. 10 Solution path of the OCP and corresponding path in constant drift (Case C).

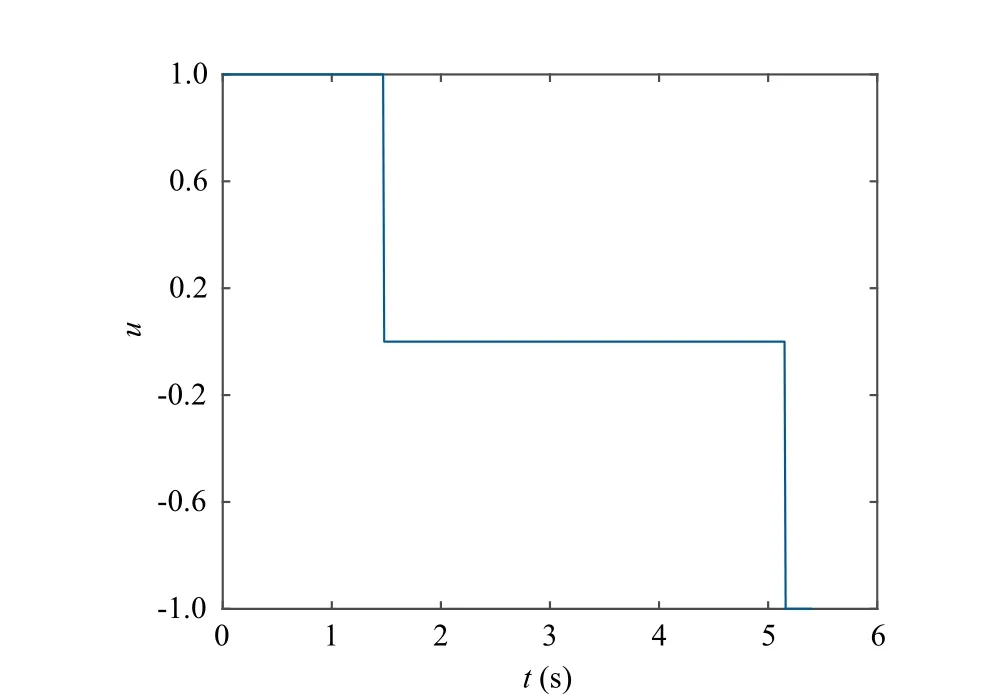
Fig. 11 Optimal control profile against time (Case C).

It should be noted that the optimal control strategy for both paths in Fig. 10 are the same. The optimal paths with four different impact angles are plotted in Fig. 12.

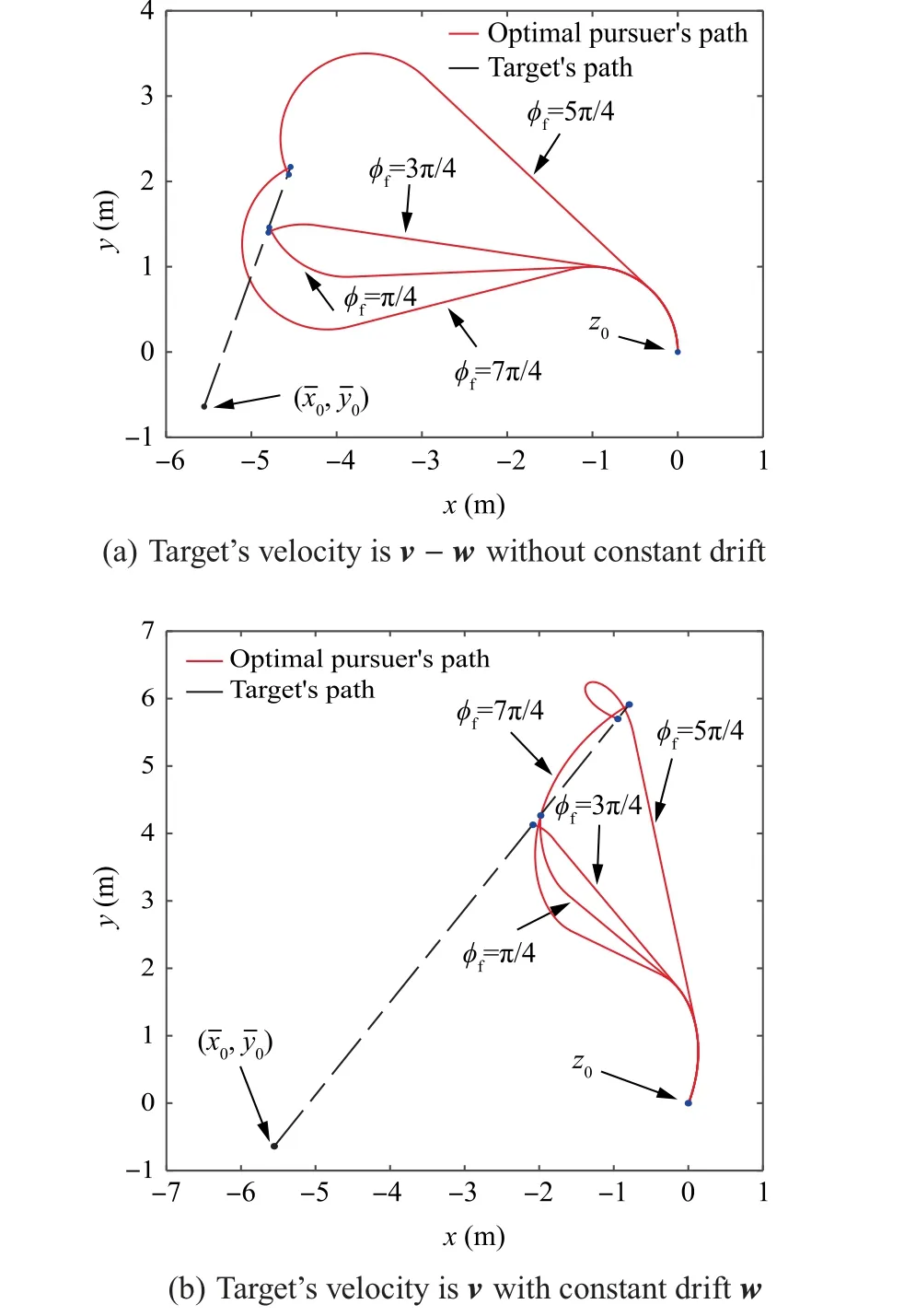
Fig. 12 Solution paths with different final impact angles and corresponding paths in constant drift (Case C).

According to the procedure in solving this example, it is concluded that the developments of the paper allow efficiently and robustly finding the time-optimal fixed-impact-angle guidance law for intercepting moving targets even if the motion of the pursuer is affected by a constant drift.

6. Conclusions

This paper is concerned with devising the time-optimal guidance law for intercepting a moving target with impact-angle constraints. The solution paths of such time-optimal guidance problems were characterized,showing that under a reasonable assumption on the distance between initial and final positions,the solution path must lie in a sufficient family of four candidates. The geometric property of each candidate was used to formulate a nonlinear equation in terms of the candidate’s parameters. As a result, computing the time-optimal guidance law was transformed to finding the zeros of those nonlinear equations. As each nonlinear equation might have multiple zeros and existing numerical solvers could not be guaranteed to converge to the desired zero related to the optimal path,an efficient and robust method was proposed to find all the zeros of those nonlinear equations. The optimal path could be obtained by comparing the lengths of paths related to all the obtained zeros. Numerical simulations showed that the time-optimal guidance law for intercepting moving targets could be found efficiently and robustly in comparison with the existing methods in the literature. In addition, it was also shown that the developments of this paper allowed finding time-optimal fixed-impact-angle guidance law for intercepting moving targets even if the motion of pursuer was affected by constant drift.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This study was supported by the National Natural Science Foundation of China (Nos. 61903331 and 62088101) and the Shanghai Aerospace Science and Technology Innovation Fund, China (No. SAST2019-10).

α, γdβ