Adaptive event-triggered distributed optimal guidance design via adaptive dynamic programming

Teng LONG, Yan CAO, Jingliang SUN,*, Guangtong XU

a School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China

b Key Laboratory of Dynamics and Control of Flight Vehicle, Ministry of Education China, Beijing 100081, China

c Department of Precision Instrument, Tsinghua University, Beijing 100084, China

KEYWORDS Adaptive dynamic programming;Distributed control;Event-triggered;Guidance and control;Multi-agent system

Abstract In this paper, the multi-missile cooperative guidance system is formulated as a general nonlinear multi-agent system. To save the limited communication resources, an adaptive eventtriggered optimal guidance law is proposed by designing a synchronization-error-driven triggering condition, which brings together the consensus control with Adaptive Dynamic Programming(ADP) technique. Then, the developed event-triggered distributed control law can be employed by finding an approximate solution of event-triggered coupled Hamilton-Jacobi-Bellman (HJB)equation.To address this issue,the critic network architecture is constructed,in which an adaptive weight updating law is designed for estimating the cooperative optimal cost function online.Therefore, the event-triggered closed-loop system is decomposed into two subsystems: the system with flow dynamics and the system with jump dynamics.By using Lyapunov method,the stability of this closed-loop system is guaranteed and all signals are ensured to be Uniformly Ultimately Bounded(UUB). Furthermore, the Zeno behavior is avoided. Simulation results are finally provided to demonstrate the effectiveness of the proposed method.

1. Introduction

With the rapid development of modern military systems,various kinds of high-speed large-maneuvering intelligent flying targets emerge in the past decades, which poses huge challenges in the traditional one-to-one guidance strategy. In order to enhance the interception probability and survivability of missiles,and further improve the missile deterrent,the cooperative guidance strategy has received increasing attention over the recent years.Compared with the traditional one-to-one guidance method using a high-technology and high-cost missile, the cooperative guidance strategy using a group of wellorganized low-cost missiles is a more efficient and destructive guidance strategy to destroy a defensive target.

In general,the cooperative guidance can be achieved in two ways, namely, implicit cooperation and explicit cooperation.In implicit cooperation, some coordination variables, such as impact time,are often required to be predefined so that all missiles attempt to attack target on this common time independently. Essentially, the implicit cooperation problem becomes a one-to-one guidance problem with impact time constraints.Ref. 5 developed the impact-time constrained guidance law to achieve simultaneous attack.However,just as the above statement,a suitable common impact time variable should be determined in advance during this cooperative guidance process,which may lead the simultaneous attack to fail due to the differences of speeds or accelerations among missiles. On the other hand,in explicit cooperation,the predetermination of the common impact time is not required,in which all missiles communicate with each other to synchronize their impact time.Therefore,the explicit cooperative guidance strategy is considered as a more advanced and intelligent guidance method,which has been gained much attention by researchers.

Generally, the cooperative guidance issue usually requires the missiles’ time-to-go estimates or range-to-go to be consensus. In Ref. 6, the distributed guidance law was proposed against a stationary target by synchronizing the time-to-go estimates. Similar to Ref. 6, Ref. 8 developed the cooperative guidance law through guaranteeing the missiles’ time-to-go to reach agreement, in which the time-varying navigation ratios were presented. In Ref. 9, the cooperative proportional navigation with a time-varying navigation gain was developed based on the time-to-go.However,the above cooperative guidance problems are mainly addressed as the consensus of missiles’ time-to-go. These methods are efficient for attacking the target with small maneuvers since the time-to-go is usually associated with future flight conditions. Once the target maneuver is unknown, this time-to-go variable becomes difficult to estimate accurately, thus leading to the failure of guidance task. To overcome this issue, in Ref. 10, the range-to-go variable is used to be synchronized, which relaxes the estimation of the missile’s time-to-go. Nevertheless, most of the aforementioned results were developed without any sort of optimality, except for Refs. 4,11. In Refs. 4,11, a centralized guidance method that requires global information of all missiles was proposed, which is impossible to be applied in large-scale swarm guidance issue.

Theoretically, the distributed guidance problem can be addressed as a multi-agent target tracking issue from the control perspective, in which multiple missiles attempt to track a maneuvering target cooperatively by decreasing the synchronization error. Although several multi-agent target tracking methodshave been developed, these results mainly focus on the system’s stability while the optimality of controller is ignored. It is necessary and significant to guarantee the optimality of controller for saving the control energy and improve the tracking performance for the practical vehicles, especially for the Unmanned Aerial Vehicles (UAVs), missiles, etc. Nevertheless,the distributed optimal guidance problem for nonlinear multi-missile system often falls into solving the coupled Hamilton-Jacobi-Bellman(HJB)equation.This HJB equation is usually intractable to obtain its exact solution analytically because of the nonlinearity and coupling properties. Fortunately, Adaptive Dynamic Programming (ADP) technique has been applied to the distributed optimal control problem of nonlinear multi-agent system, which is a promising and effective technique for the study of distributed optimal guidance problem. In Ref. 15, the distributed optimal consensus problem was investigated by combining ADP technique and fuzzy logical systems.Subsequently,Ref.16 developed the distributed optimal tracking control strategy for linear multiagent systems by using differential games, in which the criticactor architecture was constructed. Considering the unknown system dynamics, Zhang et al.presented a data-driven optimal consensus algorithm, where the traditional model identification was not required any more. Moreover, in Ref. 18, by introducing predefined extra compensators, the optimal consensus control was studied without requiring the model information.However,these developed results are mainly obtained based on the traditional time-triggered strategy, in which the data sampling and the update of controllers are both periodical.It would inevitably cause the energy consumption and time waste. Especially, in the practical engineering, the available communication and computational resources for controllers are usually limited, which requires that the developed controller is able to stabilize the control system with small resources.

Recently, the event-triggered control has become a new trend in control community. Compared with the timetriggered control,a clear advantage of event-triggered manner is that the controllers are not updated and hold constant until certain conditions are satisfied. More recently, the eventtriggered-driven nonlinear optimal control by using ADP technique has been paid much attention, and many representative results have been presented in Refs.19–23.Among them,Ref.19 studied the constrained event-triggered nonlinear optimal control,in which the updating manner of controller was aperiodic while the weights of actor-critic framework were still calculated in a periodic manner. Wang et al.studied the robust adaptive critic control based on event-triggered mechanism, which simplifies the popular actor-critic framework as a single critic network. Subsequently, based on the adaptive critic framework, Yang et al. investigated the nonlinear event-triggered ADP control with unmatched uncertaintiesand unknown dynamics.Note that, unlike the traditional actor-critic framework estimating the control policy and cost function through constructing two independent networks, the adaptive critic method removes the actor network for reducing the computation complexity as well as design complexity. It is simpler to implement the ADP controller than actor-critic network.Considering the fact that the weight values of actor network ultimately converge to the weight values of critic network for solving the associated HJB equation,the optimality of controller can be guaranteed. Although the study of eventtriggered ADP technique has made some progress, the eventtriggered distributed optimal control problem of nonlinear multi-agent systems has not been investigated,except for Refs.26–28. However, the work of Refs. 26,27 were mainly developed for the nonlinear interconnected systems, which is quite different from the cooperative control through utilizing the communication topology.In addition,considering a linear system, the event-triggered consensus problem is investigated,which is not suitable for the nonlinear systems. Briefly, the event-triggered distributed optimal control issue is still an open issue, not to mention the research on event-triggered distributed guidance problem. Therefore, it should be widely studied to deal with the distributed guidance issue for reducing the computational burden and guaranteeing the optimality of the control performance.

Based on the above analysis, this paper focuses on dealing with the distributed optimal control problem based on eventtriggered mechanism, rather than time-triggered mechanism.By designing a synchronization-error-driven adaptive triggering condition, the distributed optimal control algorithm can be implemented within the critic NN architecture, in which the critic weight vector is updated in a periodic timetriggered manner. The stability of closed-loop system is guaranteed and the Zeno behavior is excluded theoretically.

The main contributions of this paper are mainly twofold.

(1) Unlike Refs. 29–31 where the distributed optimal control scheme was designed through updating the controller periodically, in this paper, the synchronization-error-driven adaptive cooperative event-triggered mechanism is designed for updating the distributed optimal controller, thus reducing the number of controller’s update and saving the limited computational resources.

(2)Compared with Ref.32,a novel time-triggered updating law of critic weight without requiring the initial stabilizing condition is designed for simplifying the choice of design parameters.Furthermore,this proposed updating law is convenient to guarantee boundedness of synchronization error for cooperative guidance issue and exclude the infamous Zeno behavior theoretically, which facilitates the implementation of guidance law.

2. Preliminaries and problem statement

In this section,the cooperative guidance problem is formulated firstly. Then, some basic preliminaries and the general distributed optimal control problem are provided.

2.1. Cooperative guidance problem formulation

As shown in Fig. 1, a scenario is considered, where N missiles attempt to attack a maneuvering target simultaneously.Define Mand T as the i th missile and the target, respectively.V,V,i=1,2,∙∙∙,N are the velocities of the i th missile and target, respectively. θ,α,β represent the Line of Sight (LOS)angle, the Flight Path Angles (FPA) of missile and target,respectively. The control inputs perpendicular to the velocity vector are uand v,respectively. Moreover, we define the relative range between the i th missile and target along the LOS as r. In addition, we assume that all missiles and target are engagement at a constant speed during the terminal guidance process.

Fig. 1 Cooperative guidance engagement geometry.

where (x,y),(x,y) and a,adenote the (x, y) coordinates and the lateral accelerations of the i th missile and the target, respectively. In addition, τand τare autopilot scalars. In this paper, we assume τ=τ=0∙1 s.

Observing the dynamics Eq. (1), we find that when r→0,the internal dynamics f(x)→∞, which is unfeasible for the system Eq.(4).Actually,based on the guidance principle,there exists a minimum distance εsatisfying the fact that when r≤ε, the guidance process is over. In addition, one can find

Remark 1. The existing cooperative guidance strategies, such as in Refs. 6,33, require all the time-to-go to reach agreement in order to guarantee simultaneous attack. In this case, the time-to-go should be precisely estimated, which is usually infeasible when the target maneuver is unknown. In this scenario, the missile’s time-to-go is difficult to derive accurately due to the unknown future flight conditions.Therefore,unlike the existing methods addressing the cooperative guidance problem as a synchronization issue of time-to-go estimates,this paper focuses on the synchronization of ranges-to-go. A clear advantage of this strategy is to avoid the estimation of missile’s time-to-go. Obviously, if we guarantee that the ranges-to-go r, i=1,2,∙∙∙,N reach agreement, and decrease to zero synchronically, all the missiles will hit the target simultaneously.

2.2. Graph theory

2.3. General time-triggered optimal control problem description

Based on the dynamics Eq.(2),the cooperative guidance issue can be formulated as a cooperative control problem of general nonlinear multi-agent systems. Each missile is simplified as an independent controllable agent. Naturally, the dynamics of missile-target engagement is described by an affine nonlinear form, such that

3. Event-triggered distributed optimal control design

3.1. Event-triggered distributed optimal control formulation

Clearly, if the triggering condition Eq. (21) holds, then Eq.(26) implies ˙L(t)≤-ηλ(Q)‖e‖<0 for any e≠0.Thus, the closed-loop system is guaranteed to be asymptotically stable.

Remark 4. Based on Theorem 1, the triggering instant tcan be obtained through the triggering condition Eq. (21). However, the infamous Zeno behavior occurs, when the minimal intersample time (Δt)=0 (note: Δt=t-t, k ∊N).Therefore, the sample frequency parameter ηshould be properly chosen to guarantee the threshold zto be positive.

3.2. Online implementation of controller under ADP framework

Remark 7. The Persistency of Excitation (PE) is usually necessary for parameters identification of the critic network for estimating the function J(e). Generally, just like most existing literature, in this paper, an additional bounded exploratory signal should be injected to satisfy this condition when the proposed distributed strategy is implemented.Certainly, an alternative method to relax this PE condition is to use the experience replay technique, which can be found in Refs. 34,38. In this case, the update law of ︿Wcan be designed as

4. Stability analysis

To discuss the system’s stability, two assumptions about the control function g(x) and critic network are required. Note that these assumptions have been widely applied, such as in Refs. 16,20,39

Remark 8. For a general practical system,the function g(x)is always bounded since any practical actuator is physical limitation. Without loss of generality, assume that g(x) is bounded by the event-triggered error zi (t)that is related with the variable x. In addition, we assume that the NN weight,activation function and approximation error in Assumption 3 are all bounded, which is also a common assumption that has been widely applied.Note that,these boundary values are only necessary for discussing the stability rather than controller design.

Remark 10. Unlike the existing resultsdesigning the cooperative controller without considering the optimality of controller to decrease the synchronization error, in this paper,a distributed optimal controller for the nonlinear multi-missile system is designed to guarantee that all missiles are able to intercept a maneuvering target simultaneously. It ensures the stability of closed-loop system as well as the optimality of controller. In addition, compared with the popular cooperative guidance methods in Refs. 2,43,44, an obvious advantage of this paper is that an adaptive event-triggered manner is utilized to update the guidance law, rather than the traditional timebased periodic manner. It can significantly reduce the number of guidance law update as well as ensure the system’s stability,which saves the computational and communication resources for the large-scale swarming guidance systems.

5. Simulation

In this part,it is considered that two following missiles and one leading missile attack a given maneuvering target. We assume that their velocities are V=600 m/s and V=400 m/s,respectively. All missiles are able to communicate with each other under a digraph presented in Fig. 2, where M0 denotes the leader missile, and M1, M2 denote the following missiles 1 and 2, respectively.

In what follows,two scenarios are considered to implement the proposed event-triggered distributed cooperative guidance law for attacking the maneuvering target.

Scenario 1. Intercepting a constant maneuvering target

It is assumed that the target attempts to escape the interception with a=3g m/s,where g=9∙8 m/s.The initial coordinates and the initial FPAs are given in Table 1.

In addition,in order to provide the reference signal,the leader missile is driven by using a predefined PN guidance law,such that u=N˙r˙θ, where N=5, to guarantee that the leader missile hits the target. Then, the reference signal x=[r, ˙r]can be used for implementing the cooperative guidance law.

Fig. 2 Communication topology of missiles.

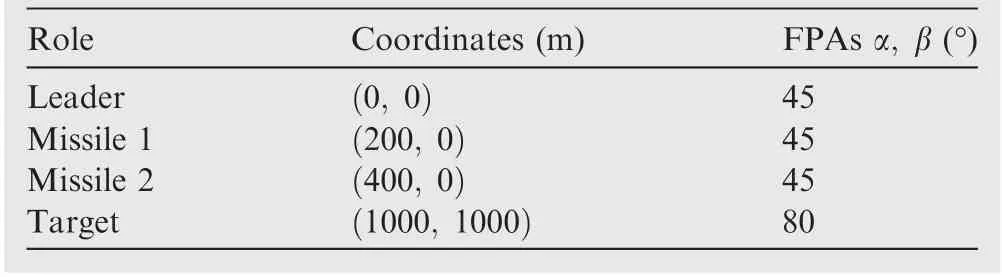
Table 1 Initial coordinates and FPAs for Scenario 1.

The cooperative interception trajectory is presented in Fig.3,which illustrates that the simultaneous interception task can be finished successfully although their initial positions are different. It further demonstrates that the two following missiles exchange their guidance information under the proposed cooperative guidance strategy to guarantee the relative range rto reach synchronization, just as shown in Fig. 4. Specifically,the summary of final miss distance and attack time of all missiles is presented in Table 2, from which, one can easily find that all missiles attack the target at about 5.9 s with an acceptable miss distance. Although the missile 2 hits the target slightly earlier than other missiles (the attack time error is 0.03 s), this attack time error is small enough to neglect in practice. Furthermore, from Figs. 4 and 5, the relative range rwill be kept consistent with each other when the range rates reach consensus.Therefore,the aforementioned three demands are all satisfied, which illustrates the effectiveness and feasibility of the proposed method.The lateral acceleration of missiles 1 and 2 are presented in Fig. 6, which are calculated and updated when the triggering threshold is violated. The evolution process of ︿Wis presented to clarify the convergence of adaptive updating law in Fig. 7.

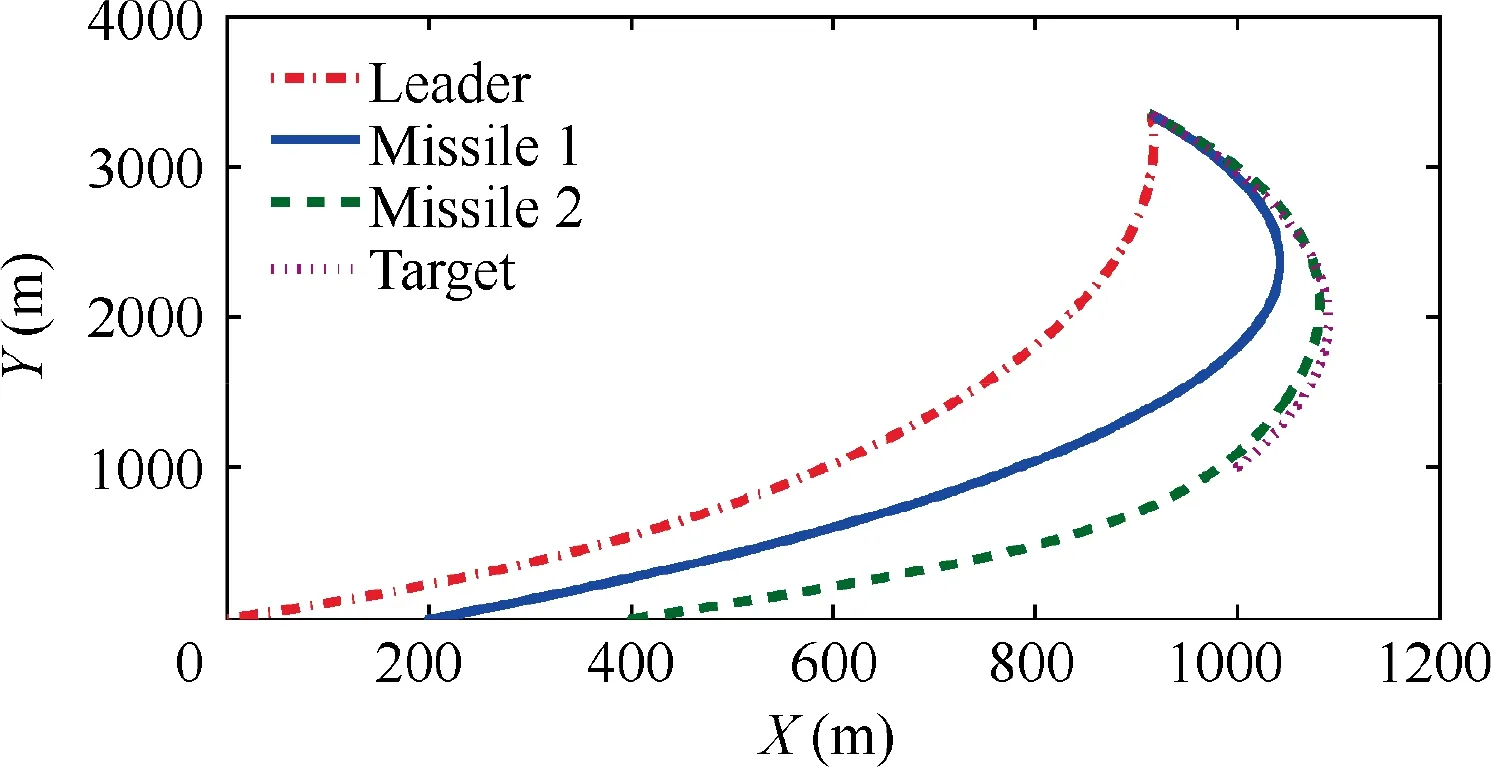
Fig. 3 Interception trajectories with constant maneuver.

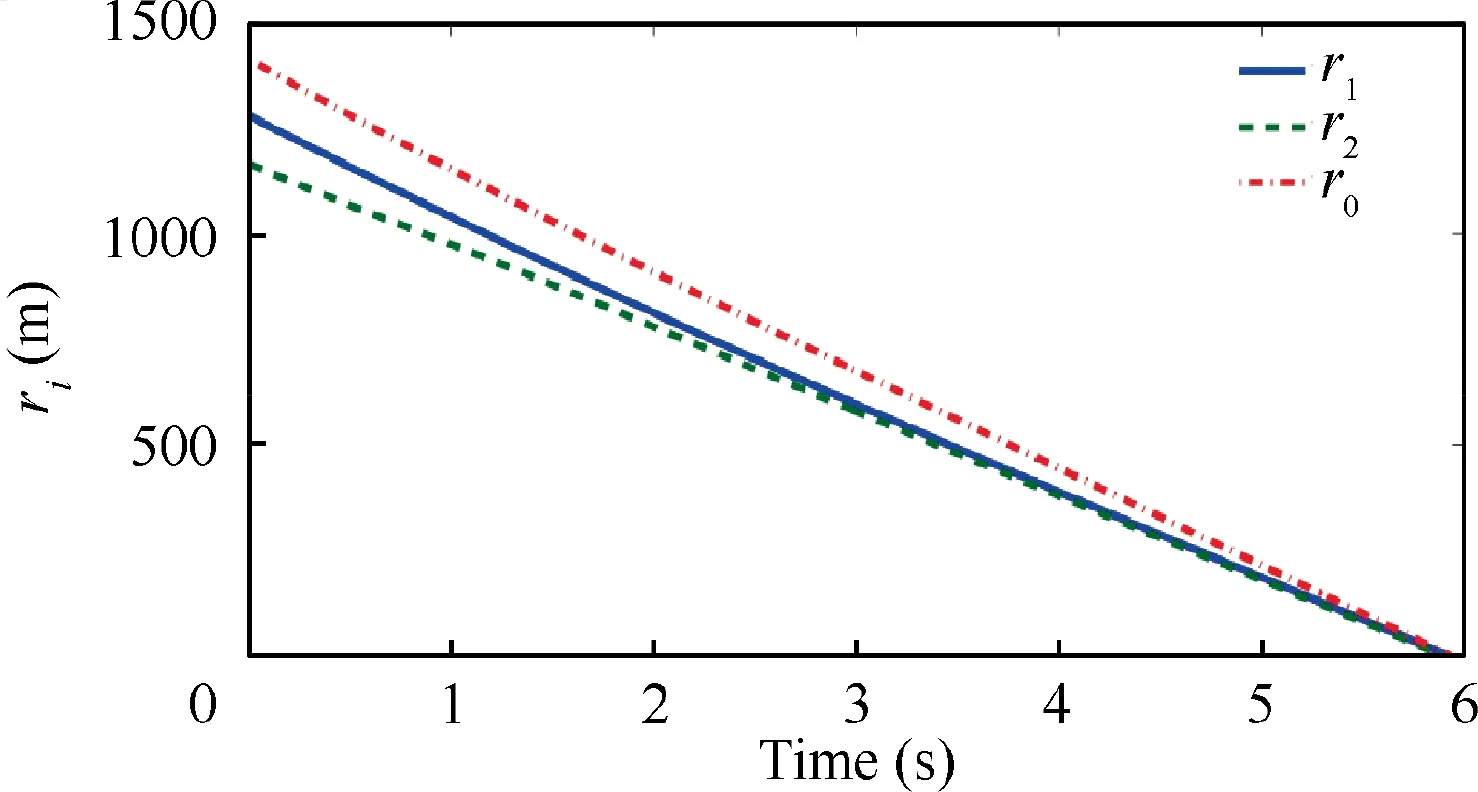
Fig. 4 Relative rangeri, i=0,1,2with constant maneuver.

Table 2 Guidance performance with constant maneuver.

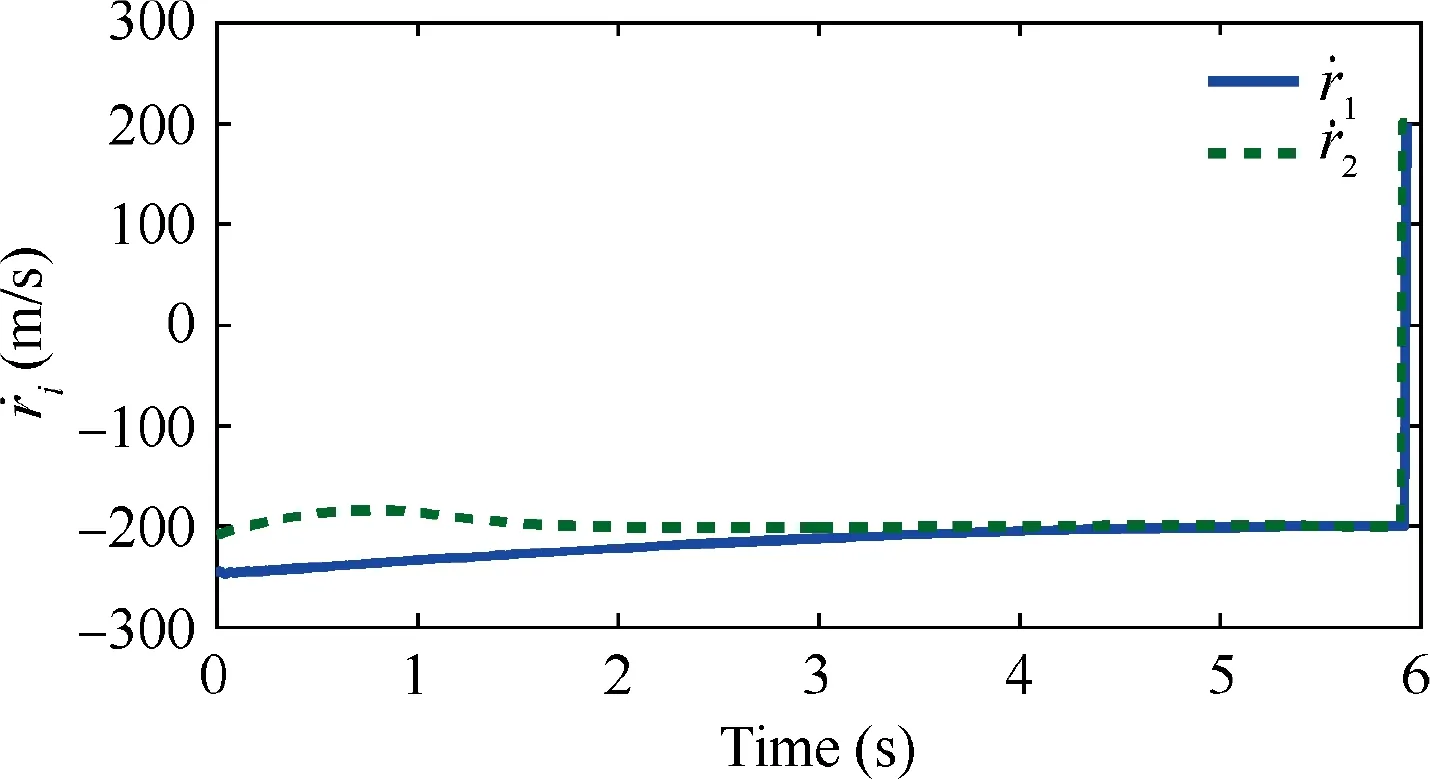
Fig. 5 Range rate ˙ri,i = 1,2 with constant maneuver.

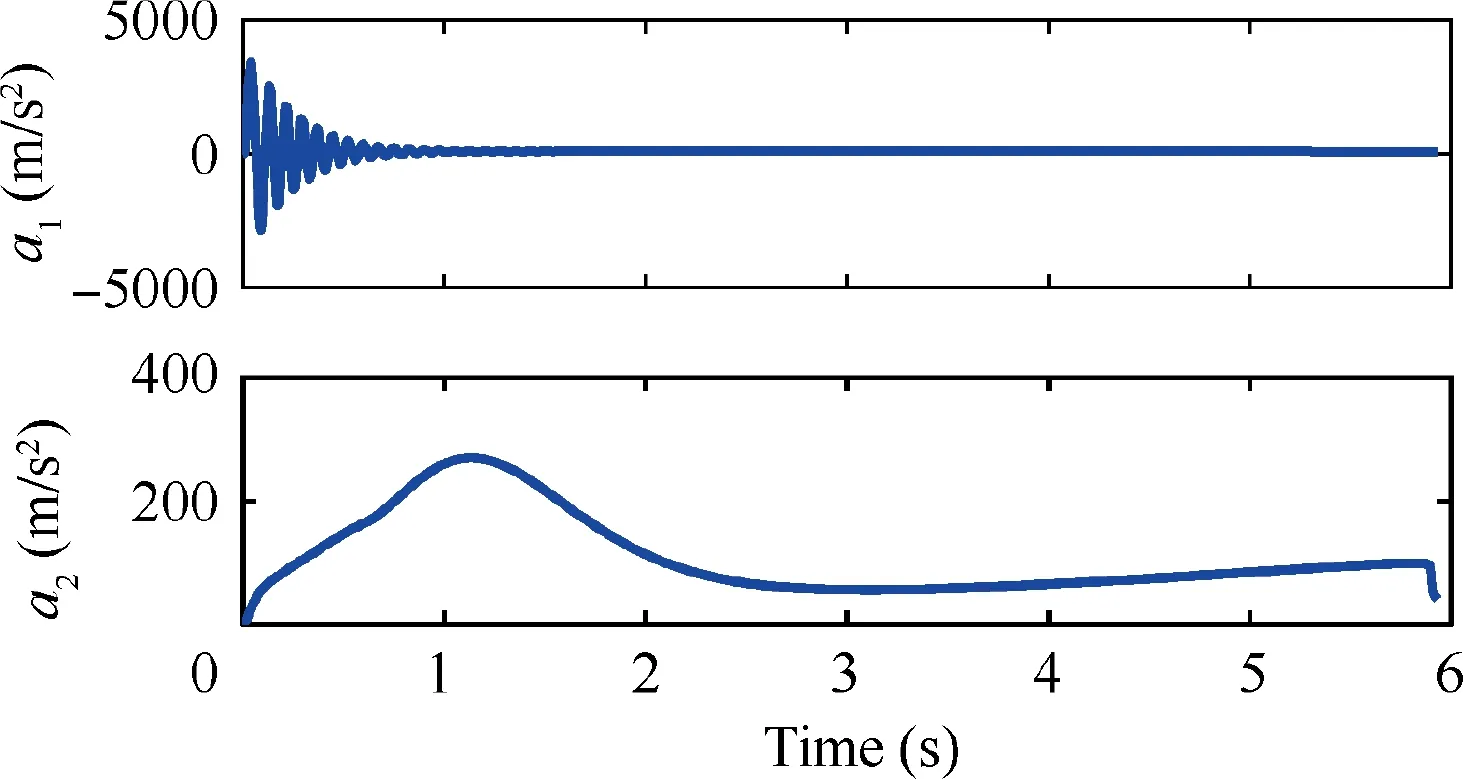
Fig. 6 Lateral acceleration ai,i = 1,2 with constant maneuver.

Fig. 7 Norms of critic network weight with constant maneuver.

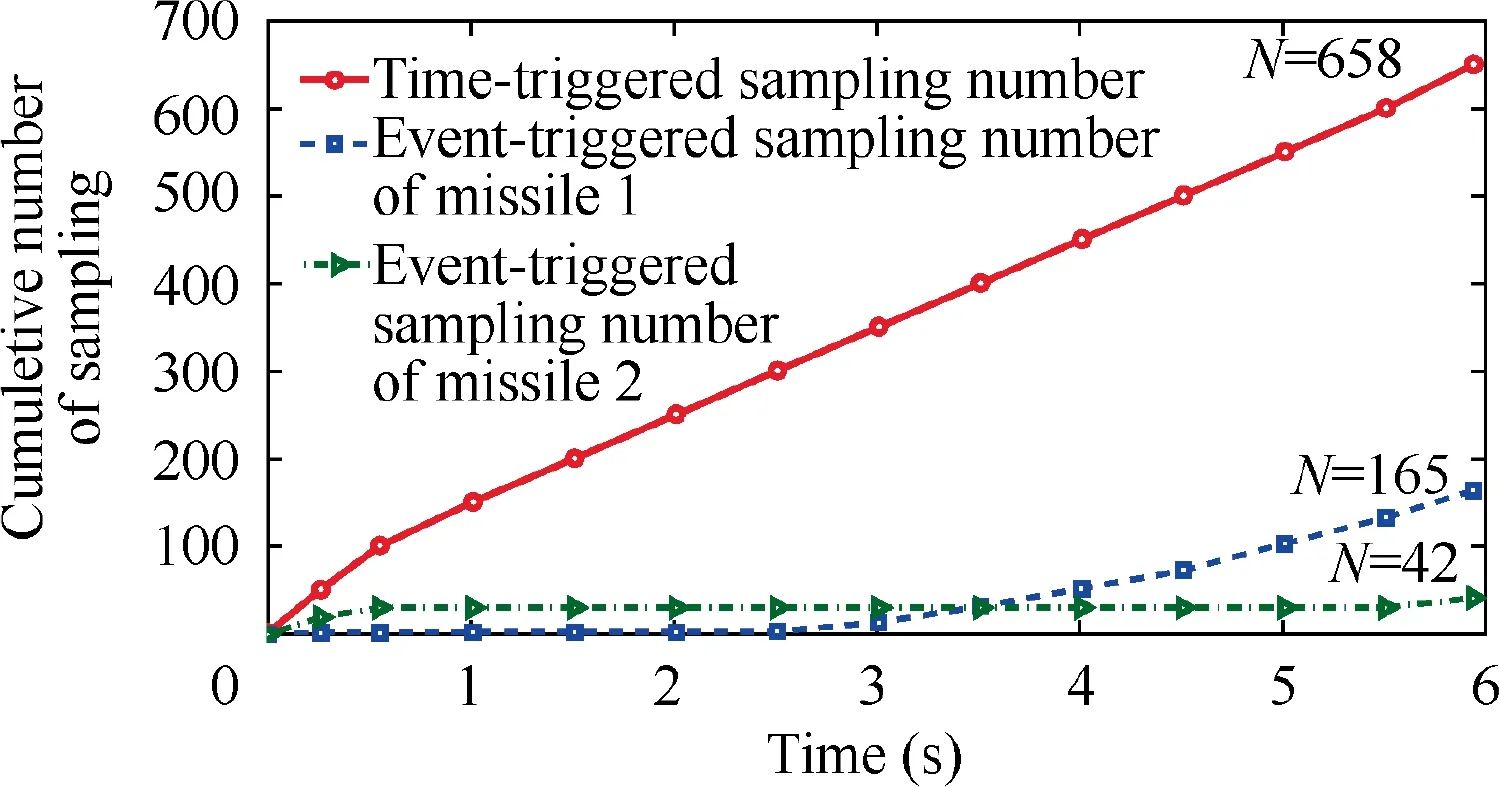
Fig. 9 Sampling number comparison with constant maneuver.

In addition,the sampling periods of the two following missiles are given in Fig. 8(a)-(b), which shows that the adaptive triggering condition is lower bounded. Fig. 9 gives the sampling number comparison between time-triggered scheme and the proposed event-triggered one. Note that the proposed event-triggered scheme needs 165 samples for missile 1 and 42 samples for missile 2, while the time-triggered one requires 658 samples. Thus, the number of controller updates can be reduced by 74.9% for missile 1 and 93.6% for missile 2 compared with the traditional time-triggered one.

Scenario 2. Intercepting a Sin-wave maneuvering target

In this case, we assume a=100sin(2t)m/s. The initial coordinates are given in Table 3. Similarly, the PN guidance law is applied for leading missile.

The design parameters are given as follows: For missile 1,we select Q(e)=ee, R=1,R=20. The learning rate is α= 0∙5, η= 0∙5 and λ= 50. For missile 2, we have Q(e)=ee, R=100,R=1, α= 0∙04, η= 0∙4,λ= 0∙6. The other parameters are chosen as the same as those in Scenario 1.

By implementing this event-triggered guidance law,the simulation results are given in Figs. 10-16. Their initial relative ranges rare obviously different since the initial positions and FPAs of all missiles are different.Considering the fact that the velocities of all missiles are same,the missiles have to cut corners or take detours to shorten or delay the attack time to guarantee the synchronization of relative ranges.To be specific,the missile 2 takes detours to delay the attack time to ensure that their rel-ative ranges reach agreement,as shown in Fig.10.From Table 4,one finds that the target can be intercepted by missiles at 2.98 s.Their final miss distances are all less than 1 m,which is an acceptable and satisfactory guidance result.Figs.11-12 illustrate that all the relative ranges rand relative range rates ˙rreach synchronization,which demonstrates that the system states x, i=1,2 reach consensus.Besides,the trajectories of lateral acceleration of two missiles are presented in Fig.13.Note that the two lateral accelerations are obtained through the control inputs uand u,which are updated based on the event-triggered mechanism.Fig.14 gives the evolution trajectories of critic weight vectors.Obviously, the weight estimation error Wcan be convergent after several seconds,which implies the effectiveness of adaptive updating law.

Table 3 Initial coordinates and FPAs for Scenario 2.

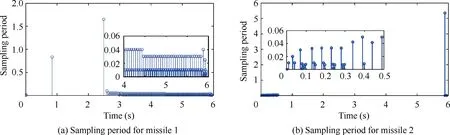
Fig. 8 Sampling period for each agent during learning phase with constant maneuver.

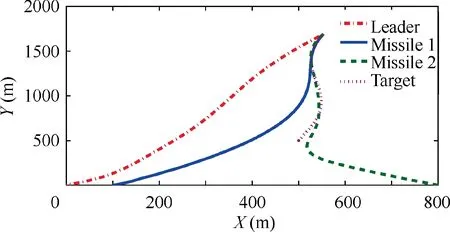
Fig. 10 Interception trajectories with Sin-wave maneuver.

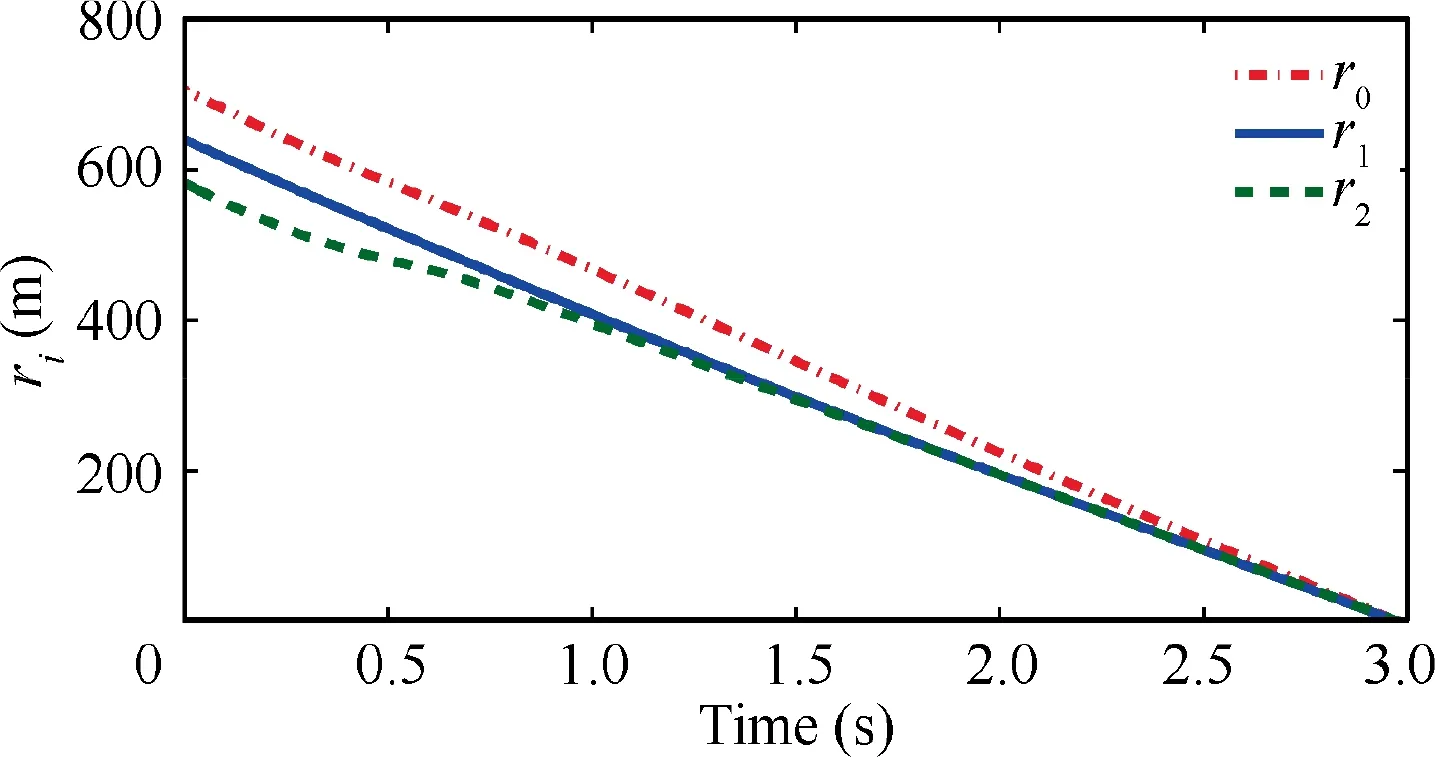
Fig. 11 Relative range ri, i=0,1,2 with Sin-wave maneuver.

Fig. 12 Range rate ˙ri,i = 1,2 with Sin-wave maneuver.

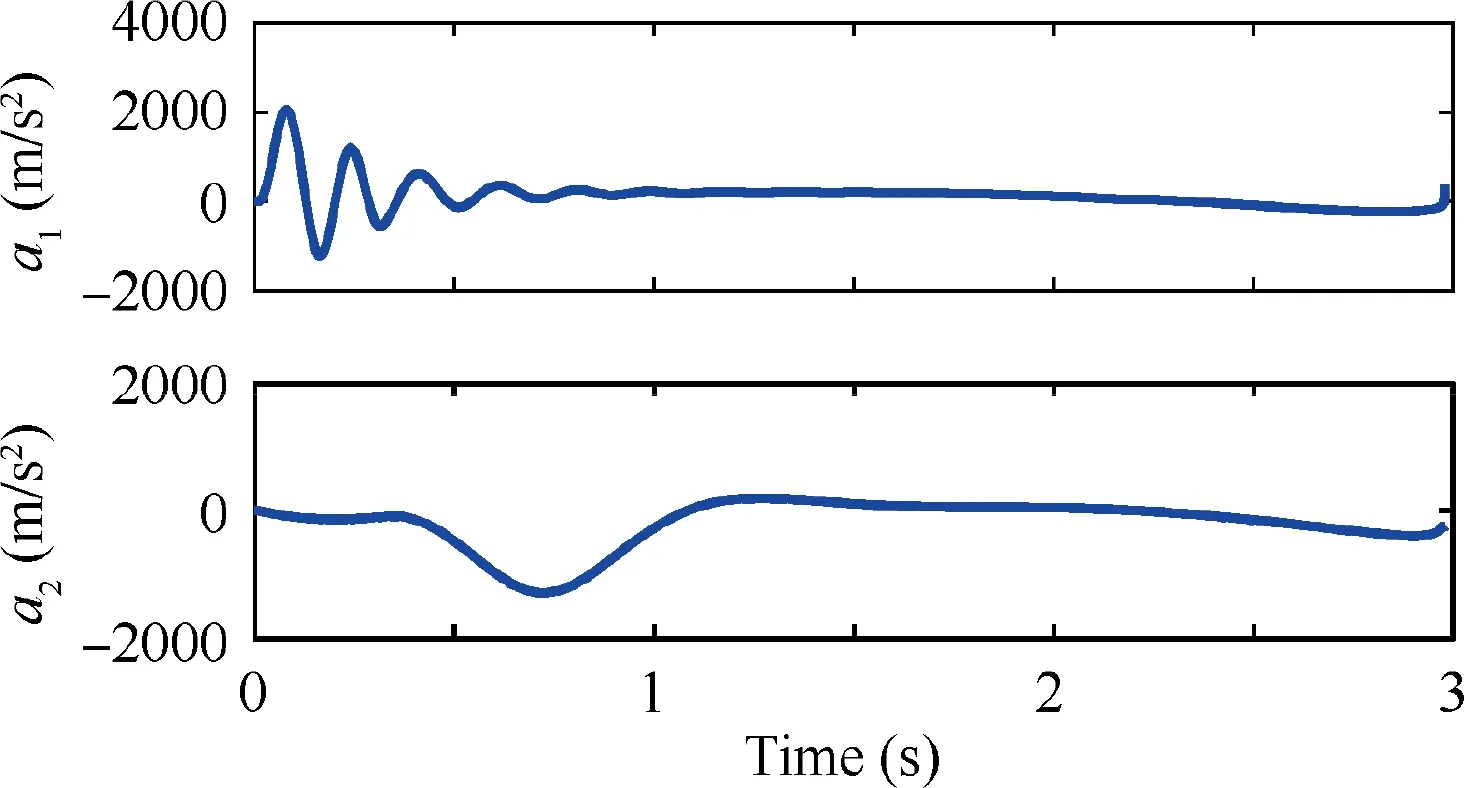
Fig.13 Lateral acceleration ai,i=1,2 with Sin-wave maneuver.

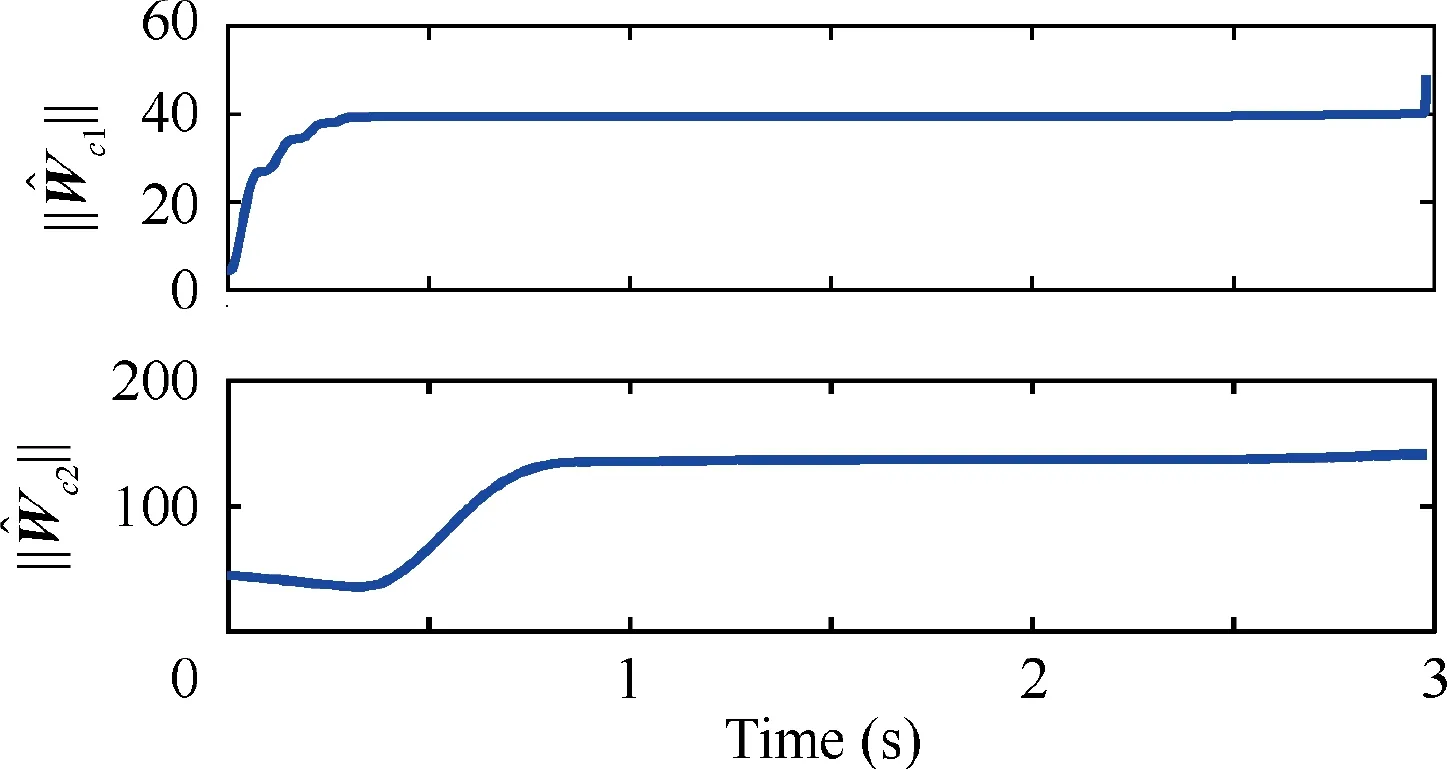
Fig. 14 Norms of critic network weight with Sin-wave maneuver.

Furthermore, the sampling periods of two following missiles are provided in Fig.15,which demonstrates that the minimal intersample time is lower bounded. In particular, Fig. 16 shows that the proposed event-triggered distributed adaptive optimal method needs only 25 samples for missile 1 and 11 samples for missile 2, while the time-triggered one requires up to 315 samples. Therefore, the computational and communication resource can be significantly reduced by 92.0% for missile 1 and 96.5% for missile 2 under the proposed method.

Furthermore, in order to satisfy the requirement of practical physical limitation,based on Scenario 1,the lateral acceleration of missile a, i=1, 2 is assumed to be bounded, i.e.,|a|≤20g m/s, i=1, 2. In this case, the proposed distributed event-triggered optimal guidance law is still implemented without any modification. The trajectories of relative ranges r, i=0, 1, 2 are presented in Fig.17,from which they can be adjusted to decrease to a neighborhood of zero simultaneously.That is,all missiles are guided to the maneuvering target and attack it at the same time. Meanwhile, the evolution trajectories of lateral acceleration a, i=1, 2 are provided in Fig. 18. One finds that the acceleration saturation phenomenon occurs since a larger control input is required for decreasing a large synchronization error caused by the difference of initial information between missiles.

On the other hand, in this scenario, the miss distance increases due to this acceleration saturation. It is because the designed guidance law does not counteract the effects of acceleration saturation initiatively and the input signal is just constrained within a physical region. Consequently, the actual input signal is not in accordance with the command input,which would inevitably affect the stability of closed-loop system.

From the above results, one concludes that the maneuvering target can be intercepted simultaneously by driving the relative ranges to reach synchronization. By using the proposed distributed guidance method, all missiles’ relative ranges and range rates are guaranteed to be consensus. Besides, in the whole guidance process, the proposed distributed guidance strategy only requires the neighborhood information, rather than the global information. Moreover, as shown in Fig. 19,the classical Time-Triggered (TT) guidance law is replaced by the Event-Triggered (ET) guidance law, which significantly decreases the update frequency of guidance law,thus reducing the computational burden. Nevertheless, since the compensation mechanism of acceleration saturation is lacking, this proposed guidance method is not sufficient to deal with the constrained distributed guidance issue efficiently.

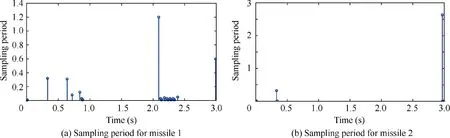
Fig. 15 Sampling period for each agent during learning phase with Sin-wave maneuver.

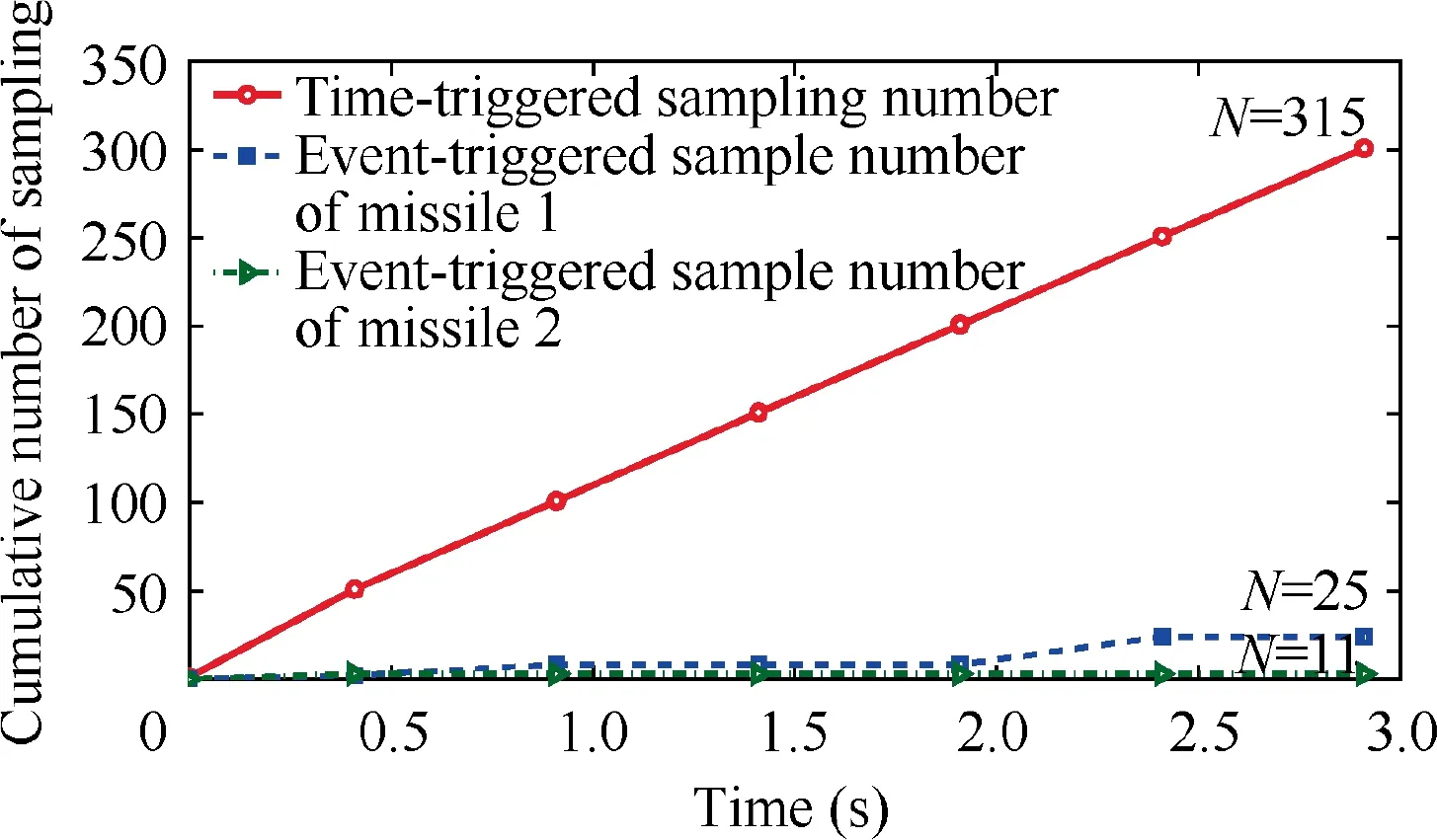
Fig.16 Sampling number comparison with Sin-wave maneuver.

Table 4 Guidance performance with Sin-wave maneuver.

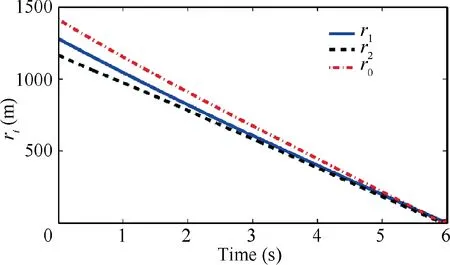
Fig. 17 Constrained relative range.

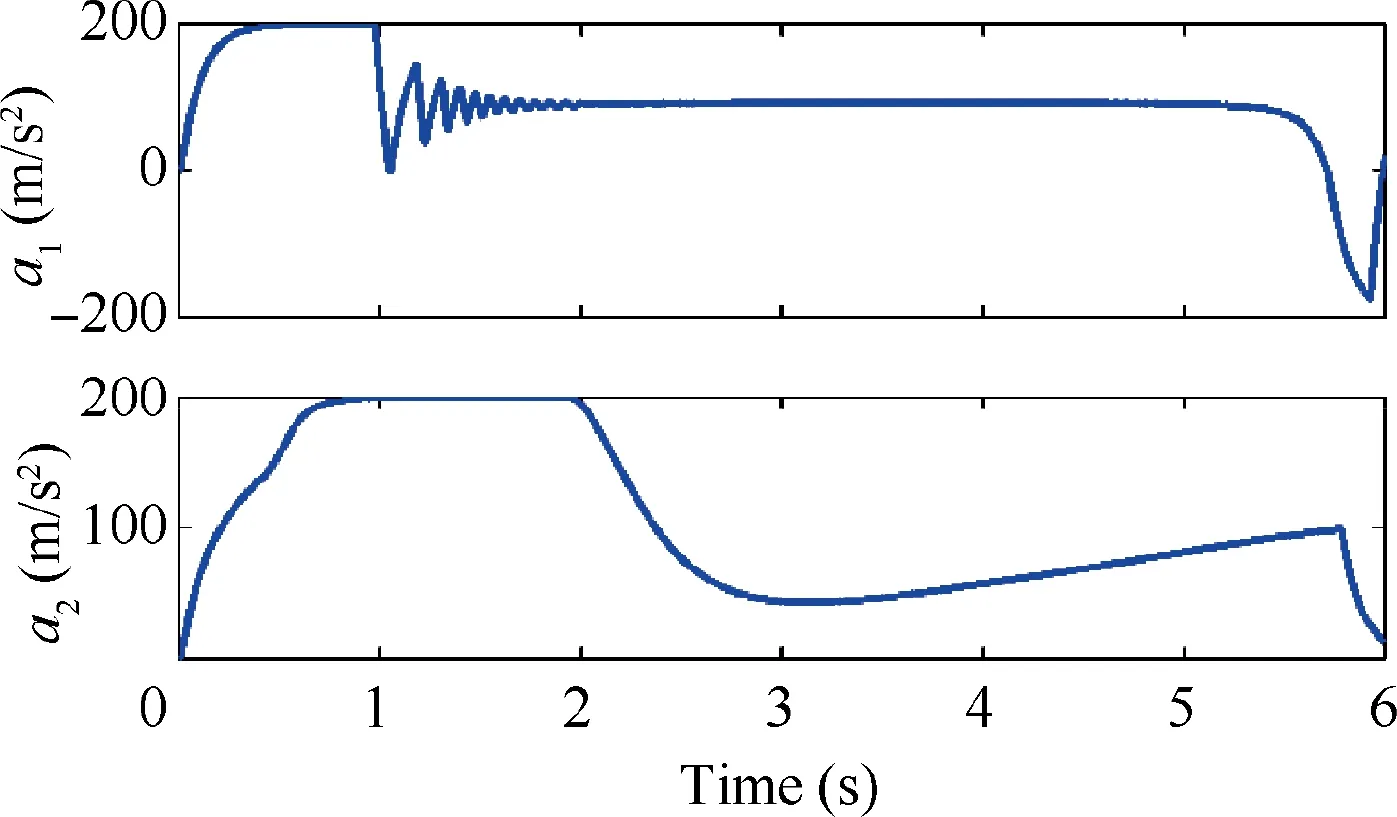
Fig. 18 Constrained lateral acceleration.

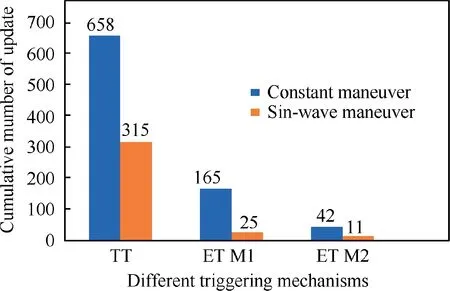
Fig. 19 Update number comparison.

6. Conclusions

This paper develops a synchronization-error-driven eventtriggered distributed optimal guidance method for multimissile cooperative guidance systems. This event-triggered guidance law is then implemented through giving an adaptive triggering condition.The weight updating law is derived based on the time-triggered mechanism by utilizing the ADP technique. After analyzing the system’s stability, the simulation results demonstrate that the proposed method can significantly save the computational and communication resource, which further exhibits the potential advantages of event-triggered mechanism. Nevertheless, more realistic constraints will be taken into consideration for guidance system to further study the mixed data and event-triggered distributed constrained adaptive optimal guidance method.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This work was co-supported by the National Natural Science Foundation of China (No. 62003036) and China Postdoctoral Science Foundation (No. 2019TQ0037).