Improving multi-target cooperative tracking guidance for UAV swarms using multi-agent reinforcement learning

Wenhong ZHOU, Jie LI, Zhihong LIU, Lincheng SHEN

College of Intelligence Science and Technology, National University of Defense Technology, Changsha 410073, China

KEYWORDS Decentralized cooperation;Maximum reciprocal reward;Multi-agent actor-critic;Pointwise mutual information;Reinforcement learning

Abstract Multi-Target Tracking Guidance(MTTG)in unknown environments has great potential values in applications for Unmanned Aerial Vehicle (UAV) swarms. Although Multi-Agent Deep Reinforcement Learning (MADRL) is a promising technique for learning cooperation, most of the existing methods cannot scale well to decentralized UAV swarms due to their computational complexity or global information requirement. This paper proposes a decentralized MADRL method using the maximum reciprocal reward to learn cooperative tracking policies for UAV swarms. This method reshapes each UAV’s reward with a regularization term that is defined as the dot product of the reward vector of all neighbor UAVs and the corresponding dependency vector between the UAV and the neighbors. And the dependence between UAVs can be directly captured by the Pointwise Mutual Information(PMI)neural network without complicated aggregation statistics. Then, the experience sharing Reciprocal Reward Multi-Agent Actor-Critic (MAAC-R)algorithm is proposed to learn the cooperative sharing policy for all homogeneous UAVs. Experiments demonstrate that the proposed algorithm can improve the UAVs’ cooperation more effectively than the baseline algorithms, and can stimulate a rich form of cooperative tracking behaviors of UAV swarms.Besides,the learned policy can better scale to other scenarios with more UAVs and targets.

1. Introduction

With the development of Unmanned Aerial Vehicle (UAV)technology, the cooperation of UAV swarms has become a research hotspot. Through close cooperation, UAV swarms can show superior coordination, intelligence, and autonomy than traditional multi-UAV systems. At the same time,Multi-Target Tracking Guidance (MTTG) in unknown environments has also become an important application direction for UAV swarms. In our MTTG problem, numerous small fixed-wing UAVs are deployed in the mission area to cooperatively track the perceived targets and search the unknown targets.But the cooperation for UAV swarms is not easy.Due to the curse of dimensionality, the computational complexity of the joint decision for all the UAVs increases exponentially with the increase in the UAVs’number.And the UAVs are partially observable, they can only communicate with the neighboring UAVs and perceive the targets locally, but cannot directly obtain the global information of the entire environment for global cooperation. Therefore, centralized cooperation that requires global information and coordinates all UAVs’actions at a central node is not feasible,and how to achieve decentralized cooperation of large-scale UAV swarms is still a huge challenge.

Due to the similarity between UAV swarms and biological flocking, several cooperation methods based on the natural flocking phenomenon were proposed, such as bionic imitation methods,consensus-based methodsand graphy-theorybased methods,etc. However, most methods simplify the complexity of the problem,such as assuming that the complex environment model is known or can be established, the UAVs can communicate globally, or the UAVs follow the designed rules, etc., which cannot meet the intrinsic characteristics of the MTTG Problem for UAV swarms. Therefore, these methods still have great difficulties in practicality.

The breakthrough progress of Multi-Agent Deep Reinforcement Learning(MADRL)technology in the game fieldverified that MADRL technology can empower agents the ability to learn coordinating behaviors. In MADRL,agents learn how to behave to maximize their rewards through repeated interactions with the environment and other agents,and learn potential coordination relationships between agents, including cooperation, competition, etc. Benefits from these,many MTTG methods based on MADRL have been proposed, such as partially observable Monte-Carlo (MC)planning,simultaneous target assignment and path planning,and other methods.However, it is challenging to extend these methods directly to the UAV swarms, because the cooperation or coordination process in most of the existing methods is centralized or requires access to global information,which is incompatible with the distributed characteristics of the swarm systems.

In the evolution of cooperation theory, reciprocal altruism is an important mechanism.This mechanism describes that when an agent interacts with other agents, its action can not only make itself rewarded, but also enable other agents to obtain a certain benefit. Inspired by this, we assume that the interactions between cooperative UAVs are also reciprocal,which means that each UAV should not only consider maximizing its reward when making an action decision, but also consider the impact of the action on other UAVs, and avoid adversely affecting their rewards. In this way, the cooperation between UAVs can be improved and the system performance can be more effective.

In this paper,we propose a decentralized MADRL method using the maximum reciprocal reward to learn cooperative tracking policies for small fixed-wing UAV swarms. Firstly,based on the MTTG problem description, we formalize this problem into a Decentralized Partially Observable Markov Decision Process (Dec-POMDP) setting. Then, inspired by the reciprocity mechanism, we define the reciprocal rewards of UAVs and proposed the calculation method of reciprocal rewards. On this basis, because of the homogeneity of UAV swarms, the experience sharing Reciprocal Reward Multi-Agent Actor-Critic(MAAC-R)algorithm based on the experience sharing training mechanism is proposed to learn a shared cooperative policy for homogeneous UAVs. Experimental results demonstrate that the proposed maximum reciprocal reward method can improve the cooperation between UAVs more effectively than the baseline algorithms, and excite the UAV swarms to emerge various cooperative behaviors.Besides, the learned policy can well scale to other cooperative scenarios with more UAVs and targets.

The major contributions of this paper are as follows:

(1) The decentralized maximum reciprocal reward method based on the reciprocity mechanism is proposed to enhance the cooperation of large-scale UAV swarms.The reciprocal reward is defined as the dot product of the reward vector of all neighbor UAVs and the dependency vector between the UAV and its neighbors. Then the reciprocal reward is used to regularize the UAV’s private reward,and the reshaped reward is used to learn the UAV’s cooperative policy using MADRL algorithms.

(2) Pointwise Mutual Information (PMI) is used to capture the immediate dependence between UAVs, where PMI can be estimated by a neural network and calculated directly without complex sampling and statistics.

(3) Based on the experience replay sharing mechanism, the MAAC-R algorithm combining the maximum reciprocal reward method and PMI estimation is proposed to learn the cooperative policy for all homogeneous UAVs.

The rest of this paper is organized as follows. Section 2 summarizes related work about the MTTG problem and cooperative learning in MADRL. Section 3 gives a brief introduction about Dec-POMDP and PMI. Section 4 describes the MTTG mission models and Section 5 details the proposed method and MAAC-R algorithm. The experimental results and discussion are presented in Section 6. Finally, Section 7 concludes this paper.

For the sake of simplicity, only those uncommon symbols are summarized in Table 1, and the definition of the default symbols in MADRL is omitted.

2. Related work

2.1. Multi-UAV tracking multi-target

Swarming is an emerging direction of multi-UAV research.There are relatively few works about UAV swarms tracking multi-target, so we can look at it from a wider perspective,multi-UAV tracking multi-target, which has been extensively studied. Therefore, here we summarize the related literature on the multi-UAV MTTG problem.This problem can be subdivided into different subtopics,such as cooperative perception, simultaneous cover and track, and multi-robot pursuitevasion, etc. Here, we summarize the general methods from two perspectives of traditional optimization and Reinforcement Learning (RL).

Table 1 Summary of notations.

A lot of methods based on traditional optimization have been published. Jilkov and Liadopted Fisher Information Matrix to design a Multi-Objective Optimization (MOO)framework to formulate the MTTG problem and presented a MOO algorithm to solve this problem. Pitre et al.also formulated this mission similarly,but they solved it using a modified particle swarm optimization algorithm. A Kalman filter was adopted in Ref.to track targets’ traces and a Consensus-Based Bundle Algorithm (CBBA) was proposed to dynamically switch each UAV’s task between searching and tracking. Petersongrouped the UAVs when their decision spaces intersect, he also designed a reward function using information-based measures, then a receding horizon control algorithm was designed to plan the best routes for all UAVs.Botts et al.formulated a cyclic stochastic optimization algorithm for the stochastic multi-agent and multi-target surveillance mission, it was demonstrated that each agent can search a region for targets and track all discovered targets.Beyond those methods, more methods based on traditional optimization theories were detailed in the review.

With the development of RL in recent years, some studies also tried to use RL methods to solve this problem. Assuming that each UAV has access to the global state and all UAVs’joint action, Wang et al.adopted a centralized RL method for UAV fleets to learn the optimal routes to maximize the perceived probability of the targets. Rosello and Kochenderferformulated the MTTG problem as a motion planning problem at the motion primitive level and used an RL method to learn each UAV’s macro action that determines to create, propagate, or terminate a target-tracking task. Qie et al.implemented the Multi-Agent Deep Deterministic Policy Gradient(MADDPG) algorithm to solve the multi-UAV simultaneous target assignment and path planning problem. However, it is assumed that each UAV can only track a single target and each target can only be tracked by a single UAV, which is not flexible and efficient for UAV swarms.

In our problem, both the UAVs and targets are homogeneous. UAVs use perception to track targets but may not be able to recognize and distinguish the identity of each target.Therefore, there is no clear allocation between UAVs and targets. Each UAV can track any perceived target, and a target can also be tracked by one or more UAVs.This creates a more flexible and extensive form of cooperation between UAVs.However, the curse of dimensionality caused by the increase in the scale of UAVs prevents most existing MADRL methods from being well-scaled to more complex scenarios.

2.2. Learning cooperation in MADRL

How to cooperate better is an important issue in MADRL.To learn the cooperation policies of agents, many methods have been proposed,including communication learning,value function factorization, centralized critic, reward modification, etc.

Communication learning. Assume that there are explicit communication channels between agents, and agents can receive communication information from others as part of their input variables. On the other hand, when making decisions,agents can not only output their actions but also output communication information sent to other agents. Reinforced Inter-Agent Learning and Differentiable Inter-Agent Learning algorithms were proposedto learn discrete communication and continuous communication information between agents,respectively, to achieve cooperation. To ensure the effectiveness and scalability of the communication method, BiCNetwas introduced to learn a bidirectionally-coordinated network between agents.CommNetwas proposed to learn a common communication model for all agents in a centralized manner.

Value-function factorization. For an environment where all agents share a common reward, methods such as QMIX,QTRAN,and VDNwere proposed to decompose the joint Q function of all agents into the sum of individual Q functions to capture the complex cooperative relationship between agents.

Centralized critic.As the name suggests,a centralized critic network is proposed to evaluate the agent’s policy, where the input of the network is the relevant information of all agents(such as joint observation and joint action). COMAcompared the actual reward and counterfactual reward to evaluate the impact of an agent’s action on the global reward. And MADDPGintroduced a critic network that can receive all agents’information to guide the training of the actor-network.

Reward regularization. This refers to quantifying the cooperation between agents and using it as an additional reward.Based on the following assumption:the actions between cooperative agents are highly correlated, Kim et al.and Cuervo and Alzatereshaped global reward with Mutual Information(MI) that captures the dependence between agents’ policies,then agents can learn cooperative policies by maximizing the reshaped reward. Wang et al.proposed EITI that used MI to capture the interactions between the transition functions of the agents. Then they also proposed EDTI to capture the influence of one agent’s behavior on the expected rewards of other agents. It has been proved that optimization by using EITI or EDTI as a regularization term can encourage agents to learn cooperative policies. Except for MI, Kullback-Leibler (KL) divergence can also be used for regularized rewards. Jaques et al.used the intrinsic social influence to reward agents for causal influence over another agent’s actions. There is an assumption that the influencer takes an action, then the influencee takes the action as part of its input variable and uses counterfactual reasoning to evaluate the causal influence of the action.Thus,the influence process between agents is nonsymmetric. Moreover, counterfactual reasoning needs to know the influencee’s policy and input variables.The MI and KL divergence used in the above regularization methods are aggregate statistics, so their calculation requires multiple sampling, and they cannot evaluate the dependence between two specific random events. Barton et al.implemented a technique called Convergent Cross Mapping(CCM)to measure the caused influence between agents’specific events (such as actions or states). However, how to choose the embedding dimension and delay time in the phase space reconstruction process of high-dimensional input variables is still a huge challenge.

In addition, some of the latest cooperative policy learning methods using MADRL were proposed for UAV swarms.

Baldazo et al.presented a MADRL method to learn the cooperative policies for fixed-wing UAV swarms to monitor floods in a decentralized fashion. But it assumes that each UAV can concatenate all UAVs’ information, this is incompatible with the partial observability of the UAV swarms,and greatly limits the scalability of the proposed method.Wang et al.developed a MADRL algorithm to learn a sharing policy for a UAV swarm,in which each UAV only directly cooperates with the nearest two neighbors on its left side and right side. However, the protocol that only captures the fixed two collaborating neighbors is too sloppy, because cooperation emergence depends on topological. Khan et al.presented a MADRL method by employing a Graph Neural Network(GNN)to learn cooperative formation flying policies for a UAV swarm.Although the GNN can extract local information of individuals,how to perform the graph convolutional operation for UAVs whose exact number is unknown and maybe changing is still a challenge.Venturini et al.proposed a distributed RL approach that scales to larger swarms without modifications in monitoring and remote area surveillance applications. However, they assume that the system environment consists of square grids and each UAV can directly share the observation with others.

The research goals of these works are similar to that of this paper, but the scales of the UAVs are not large (only a few dozen). Besides, these methods make over-idealized assumptions that ignore some inherent characteristics of UAV swarms, such as global communication, fully observable, etc.Hence,we believe that these methods may have practical issues for large-scale UAV swarms. This paper considers the largescale, partial observability, distributed decision-making,homogeneity, interchangeability, and other characteristics of the MTTG problem for UAV swarms,which makes the model more versatile and feasible.Moreover,we propose a maximum reciprocal reward method to further improve the cooperation between UAVs. Compared with the existing work, our task is more challenging,in which the UAV swarms can handle different maps and group sizes, different numbers of the targets,etc.

3. Preliminary

3.1. Dec-POMDP setting

The decision process of UAV swarms can be defined using Dec-POMDP.In Dec-POMDP,each agent can only get local observation information (including perception and communication), but cannot obtain the global state. At every step t,each agent makes its action decision based on its local observation information, and all agents execute their joint action to refresh the environment. Except for special definition, the time subscript t of variables is omitted for convenience, and the joint variables over all agents are bold.

Assuming there are n agents, the Dec-POMDP is defined as:

3.2. Mutual information and pointwise mutual information

4. Problem formalization

4.1. Problem description

Suppose a large number of homogeneous small fixed-wing UAVs and homogeneous targets are scattered in the mission scenario. The UAVs are flying at a constant speed in a twodimensional plane,their actions are the heading angular rates.The UAVs can perform emergency maneuvers, such as temporarily staggering the flying height to avoid collisions. The targets are randomly walk in the environment, and the UAVs cannot get the prior information of the targets in advance.

As shown in Fig. 1, each UAV uses onboard sensors that look down to perceive targets.When a target is within the perception range,the UAV can perceive and track the target, but the UAV cannot distinguish the target’s specific identity.Meanwhile, the UAV can receive the local communication information from its neighboring UAVs. And it can also obtain local information relative to the boundary of the mission area. Then the UAV makes its action decision based on the local information.

Due to the limited perception range of the UAVs and the uncontrollable movement of the targets, the UAVs may lose the tracked targets.And since there is no explicit target assignment, a single UAV may track multiple aggregated targets at the same time, or multiple UAVs may cooperate to track the single or multiple targets. Therefore, the UAVs should keep the targets within their field of view persistently,and cooperate in a decentralized manner to track as many targets as possible.Moreover, the UAVs should also be able to avoid collisions and fly off the boundaries, and satisfy safe constraints.

4.2. Models

Based on the overall description of the problem above, we establish the relevant models based on the Dec-POMDP paradigm as follows:

Local communication and observation models. The local communication and observation models of each UAV are illustrated in Fig. 2, where the maximum communication dis-

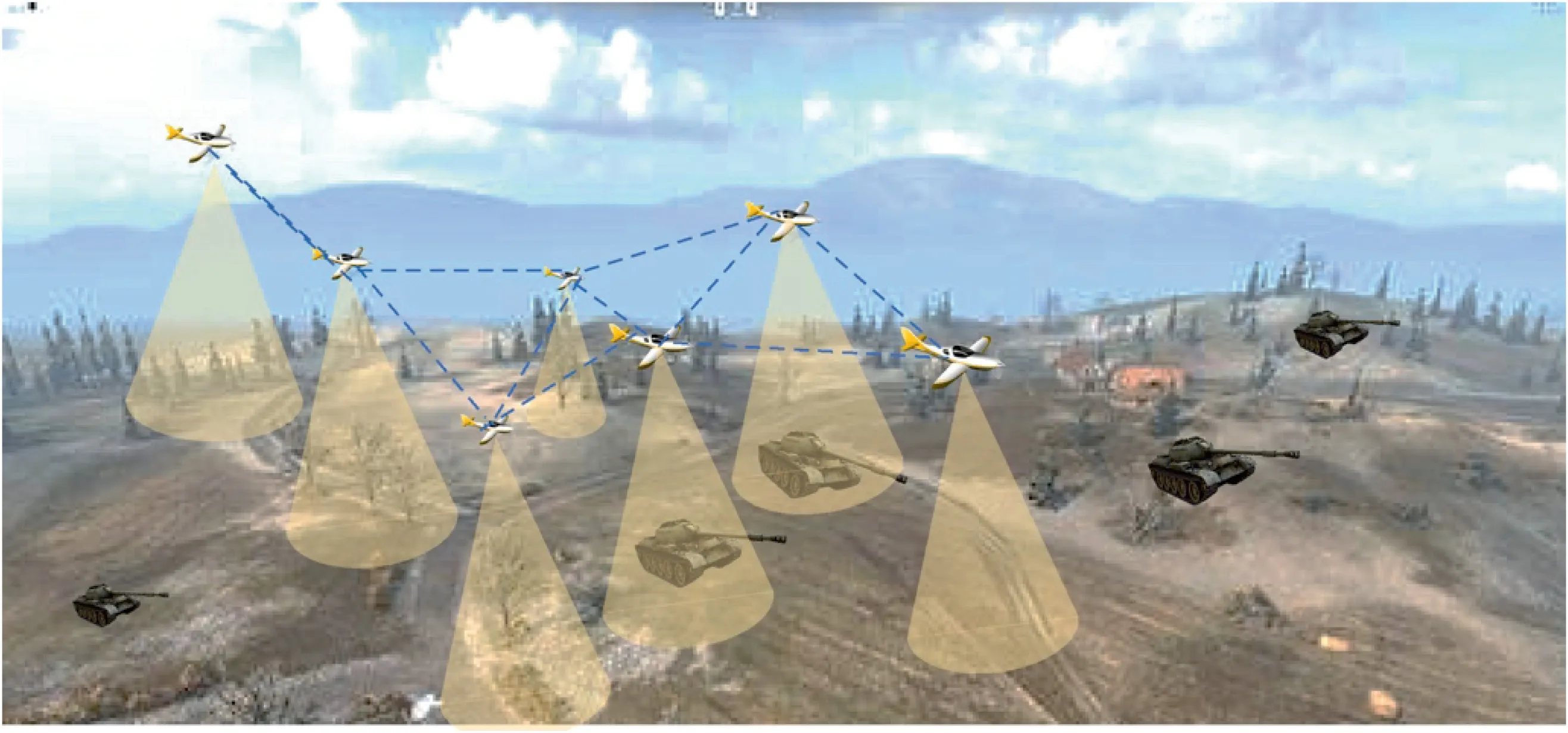
Fig. 1 Scenario of UAV swarms tracking multi-target.

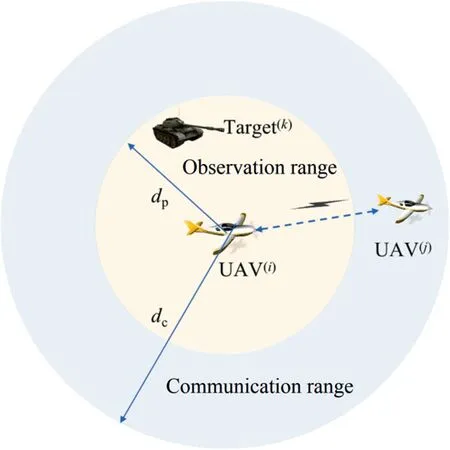
Fig. 2 The communication and observation diagrams of each UAV.

4.3. Reward shaping

To encourage the UAVs to learn cooperative policies, each UAV is supposed to not only track the already perceived targets well but also avoid overlapping perception to maximize the total perception range. Besides, they should avoid flying out of the mission scenario and ensure a safe flight. These expectations are represented by the reward shaping potentially.Thus,it is necessary to design reasonable rewards for UAVs to guide the learning process.

Tracking targets. Both the targets and UAVs are moving dynamically, and the perceived targets may move out of the UAVs’ sensing range. A naı¨ve idea is that the closer the UAV is to a target, the better the tracking effect it is. Therefore, UAV i ’s reward for tracking a target is as follows:

5. Maximum reciprocal reward method

Inspired by the mechanism of reciprocal altruism in the evolution of intelligence theory, if an agent is beneficial to other agents,the agent should be rewarded.The intuition behind this is that if an agent knows the impact of itself on other agents,it can cooperate with other agents to achieve win–win teamwork.In the MTTG problem,we assume that if a UAV can deliberately lead to cooperation with neighbors so that they can get better rewards, the UAV should be appropriately encouraged;otherwise, when the neighbor gets negative rewards, the UAV should take part of the responsibility, and therefore would be punished. Specifically, we modify each UAV’s immediate reward as:

5.1. Reciprocal reward

5.2. Pointwise mutual information estimation

The environment reward of each UAV is given, then a major obstacle in the calculation of reciprocal reward is the dependence indexes between every two cooperative UAVs. In UAV swarms, each UAV is partially observable and makes the action decision based on its local information, including communication with neighbors, observation about targets,boundary information, and state information, etc. Since all the UAVs coexist in one environment and the global state is unknown, the local information and actions between two neighboring UAVs may not be independent. We use PMI to capture the dependence between UAVs. Then the dependence index between UAV i and j is denoted as:

where N(∙) is a counter, N(l,a,l,a) is the number of occurrences of (l,a,l,a) during the sampling process,and N(L,A,L,A) is the sum of the numbers of all possible joint information-action pairs. p(o,a) and p(o,a)can also be estimated similarly. However, in a complex environment that its local information or action space is large or even continuous, MC sampling may be infeasible since the time and memory consuming.

Fortunately, we can get the optimal PMI estimation by Maximizing Mutual Information(MMI).MI can be expressed as the expectation of the divergence between the joint probability distribution and the product of marginal probability distributions. According to different measurement methods,many works that maximize the variational lower bound of MI are proposed, such as Refs.. Among them, Iestimates the MI using Jensen-Shannon (JS) divergence, which is more stable than the other methods. Inspired by mutual information neural estimation,we can also estimate PMI using a neural network.For brevity and convenience of derivation, we use xand xas the proxies of (l,a) and (l,a),respectively. Then we can estimate PMI using the following lemma.

Lemma 1. For random variables Xand X, their JS MI is defined as:

Therefore,we can use the neural network f(l,a,l,a)to estimate PMI(l,a;l,a) via maximizing I(L,A;L,A).In practice,the minimum PMI is 0 when there is no dependence between two random events, but the output of fmaybe less than 0, so we take PPMI(l,a;l,a) instead.

5.3. Algorithm construction

Due to the additional reciprocal rewards, the reshaped immediate reward of each UAV is not only related to the environment but also related to the UAV’s neighbors. In formal way, replacing the local observation in the Dec-POMDP with the local information of each UAV,and replacing the environmental reward with the reshaped reward in Eq. (7), will not change the Dec-POMDP paradigm, so the proposed method can be easily combined with the existing MADRL algorithms.

In this article, we modify the vanilla Multi-Agent Actor-Critic (MAAC) algorithm and add a step to calculate each UAV’s reciprocal rewards with its neighbors. Since all the UAVs are homogeneous and the PMI is symmetrical, the output of the PMI network should be identity irrelevant. Thus,the UAVs could share a common PMI network. When performing a cooperative mission, the homogeneity of UAVs means that their policies should also be similar. Therefore,their policies could also be shared. Using reciprocal reward to adapt the vanilla MAAC algorithm, the overview of the proposed algorithm is shown in Fig. 3.

Combined with the experience replay mechanism,we propose our experience sharing MAAC-R algorithm, as shown in Algorithm 1. In this algorithm, all UAVs’ experiences are collected to train the shared actor-critic network and PMI network, which significantly improves the diversity of the training data and benefits to improve the training efficiency and the generalization ability of the networks. Then the trained networks are published to all UAVs to execute in a decentralized fashion.

Fig. 3 Overview of the proposed algorithm.

In the process of training, we assume that each UAV can immediately obtain the environmental rewards and local information of neighboring UAVs.And,it uses the PMI network to respectively calculate the dependency index with each neighbor. The dot product of these dependence indexes and the received environmental immediate rewards is used to reshape the UAV’s environment reward. Then we can perform the update step of the MADRL algorithm using the reshaped reward, which is consistent with the update step of the vanilla actor-critic algorithm. During execution process, each UAV makes its action decision using the shared policy in a decentralized manner. The input variable of the policy is each UAV’s local information, and the output variable is the index of the UAV’s action decision, which is identity irrelevant.

Please note that during both the training and execution processes, each drone only obtains the local information directly related to it, not the global information of the environment.Thus, the proposed MAAC-R algorithm can scale well to the scenarios whose population is large and variable to achieve cooperation,which is infeasible in the methods that require all agents’ information, such as MADDPGand QMIX, etc.

Algorithm 1. Experience sharing reciprocal reward MAAC(MAAC-R)Initialize. Actor network parameters θ, evaluation network parameters φ, target network parameters φ-, AC experience replay buffer D1, PMI network parameters ω, PMI experience replay buffer D2 1. for episodes = 1:M do 2. Reset environment 3. Receive all UAVs’ joint local information l 4. for t=1:T do//Collect experience 5. For each UAV i, select action a(i) ～πθ(l(i)) w.r.t. the shared policy and exploration 6. Execute joint action a to receive joint environmental immediate reward re and refreshed joint local information l′7. for i=1:N do 8. For UAV i, get its neighbors N(i)9. for j=1:|N(i)| do 10. Calculate the cooperation index d(ij) =fω(l(i),a(i);l(j),a(j))11. Store (l(i),a(i);l(j),a(j)) into buffer D2 12. end for 13. Reshape r(i) according to Eqs. (7) and (8)14. Store (l(i),a(i),r(i),l(i)) into buffer D1 15. end for//Update actor-critic network 16. Randomly sample B1 samples (lk,ak,rk,l′k) from buffer D1 17. Set yk =rk+γQ-φ-(l′k,a′k)|a′k～πθ(l′∑k)k(yk-Qφ(lk,ak))2 19. Update θ by minimizing -18. Update φ by minimizing 1 B1 1∑klog(πθ(ak|ok))Qφ(lk,ak)20. if update target network then 21. φ- ←τφ+(1-τ)φ-22. end if//Update PMI network 23. Randomly sample B2 samples (l1k,a1k;l2k,a2k) from buffer D2 B1 24. Randomly sample B2 samples (l-2 k,a-2 k) from buffer D2 25. Update ω by minimizing ∑klog(1+exp(-fω(l1k,a1k,l2k,a2k)))+ log(1+exp(fω(l1k,a1k, l-2 k,a-2 k)))26. end for 27. end for 1 B2

6. Numerical experiment

In this section, we evaluate the proposed algorithm in the established MTTG problem. And we hope that the UAVs can learn to cooperate with their neighbors in a decentralized way,but the methods that required global information are not satisfied,such as MADDPG,QMIX,and influence of state transition, etc. Thus, the baseline algorithms include the vanilla MAAC algorithm and an ablated version of MAAC in which UAVs can receive the global reward as their common reward (named as MAAC-G).

The objective is to answer the following questions:(A)Can the reciprocal reward method improve the cooperation and performance of UAVs in the MTTG problem? (B) What did the UAVs learn using the proposed algorithm? (C) How scalable are the learned policy?

6.1. Parameters setting

According to the established models, we developed a UAV swarm tracking multi-target simulation platform.All the algorithms are trained using the same environment configuration,as shown in Table 2. And the hyperparameters are configured in Table 3.During all algorithms’training processes,we use an annealing exploration probability β ∊[0,1] to balance the exploration and exploitation issue. Specifically, at the beginning of the training process, the UAVs are supposed to fully explore the environment, so we set β=1 that encourage the UAVs to randomly select different actions in their action spaces to collect various experiences. As the training episode increase, β gradually anneals to 0, and the UAVs gradually apply the learned policy to make their action decisions.

6.2. Validity verification

According to the goal of the MTTG problem, we count the number of targets that a single UAV can track and the number of targets tracked by all UAVs respectively at each step to evaluate the performance of the algorithms.The weight parameter in MAAC-R is set as α=0∙3.

Fig.4 shows the training results of the algorithms.It can be seen from Fig. 4(a) and Fig. 4(b) that the performance of MAAC-R is better than the other two algorithms in terms of the average targets and the collective targets. The advantage of MAAC-R over the vanilla MAAC shows that in decentralized cooperation, using reciprocal rewards from neighbors toreshape the UAVs’ original rewards can effectively improve the cooperation between UAVs. Interestingly, when using MAAC-G, the numbers of the tracked targets in both subfigures first increase quickly, but then decrease immediately. It can be inferred that in UAV swarms, greedily maximizing the global reward may have a certain effect in a certain period,but the enhancement of greed may also cause conflicts between UAVs, which is not conducive to cooperation. Therefore, the proposed maximum reciprocal reward method can improve the cooperation and performance of UAV swarms in the MTTG problem.

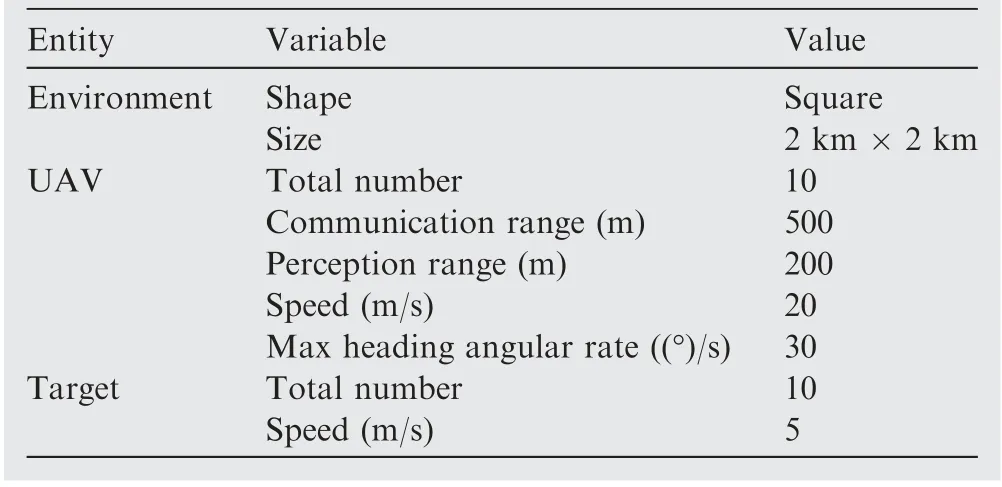
Table 2 Environment parameter settings.

Table 3 Hyperparameter configurations.

6.3. Performance test

To better evaluate the policies learned by these algorithms,we reload and execute the trained actor networks without further tuning. And the reciprocal reward is no longer required in the execution process. The parameters of the testing environment are identical to the training one, and the environment is randomly initialized before each execution episode.

Each actor-network is executed 100 episodes and the average statistical indicators are shown in Table 4.In these tests,all the statistical indicators of MAAC-R obviously outperform those of other methods.Especially,the comparison of environmental reward indicates that the introduction of the weighted reciprocal reward can improve UAVs’ environmental reward.Moreover, it can be inferred that the enhancement of cooperation between UAVs may also improve the shortcomings of the original reward shaping, which can further improve the performance of the system while increasing individual rewards.This also illustrates the significance of cooperation for UAV swarms.

To intuitively understand whether the UAVs have learned how to track targets, Fig. 5 shows the visualization of the tracking process in which UAVs execute the policy learned by MAAC-R. In Fig. 5(a), all the UAVs and targets are randomly initialized, and there are only 3 targets covered by the UAVs. Then, UAVs track more targets cooperatively by executing the learned policy and various cooperation forms between the UAVs emerge,including(A)formation:neighboring UAVs that are not tracking any targets may automatically form a formation and maintain maximum coverage (no repeated perceptions); (B) n/n : multi-UAV track multitarget cooperatively; (C) 1/n : a single UAV tracks multitarget simultaneously;(D) n/1 :multi-UAV track a single target cooperatively;(E)1/1:one UAV tracks a single target;(F)exchange: UAVs exchange each other’s tracking targets.

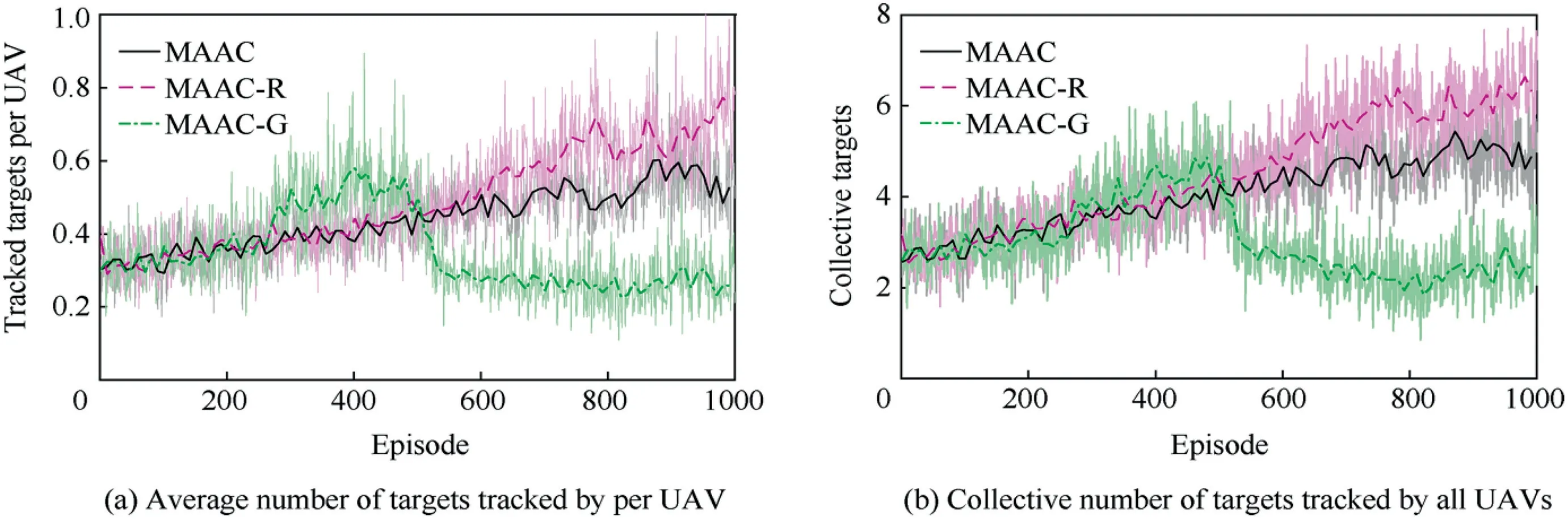
Fig. 4 Training curves of different algorithms.

Table 4 Test results statistical indicators.

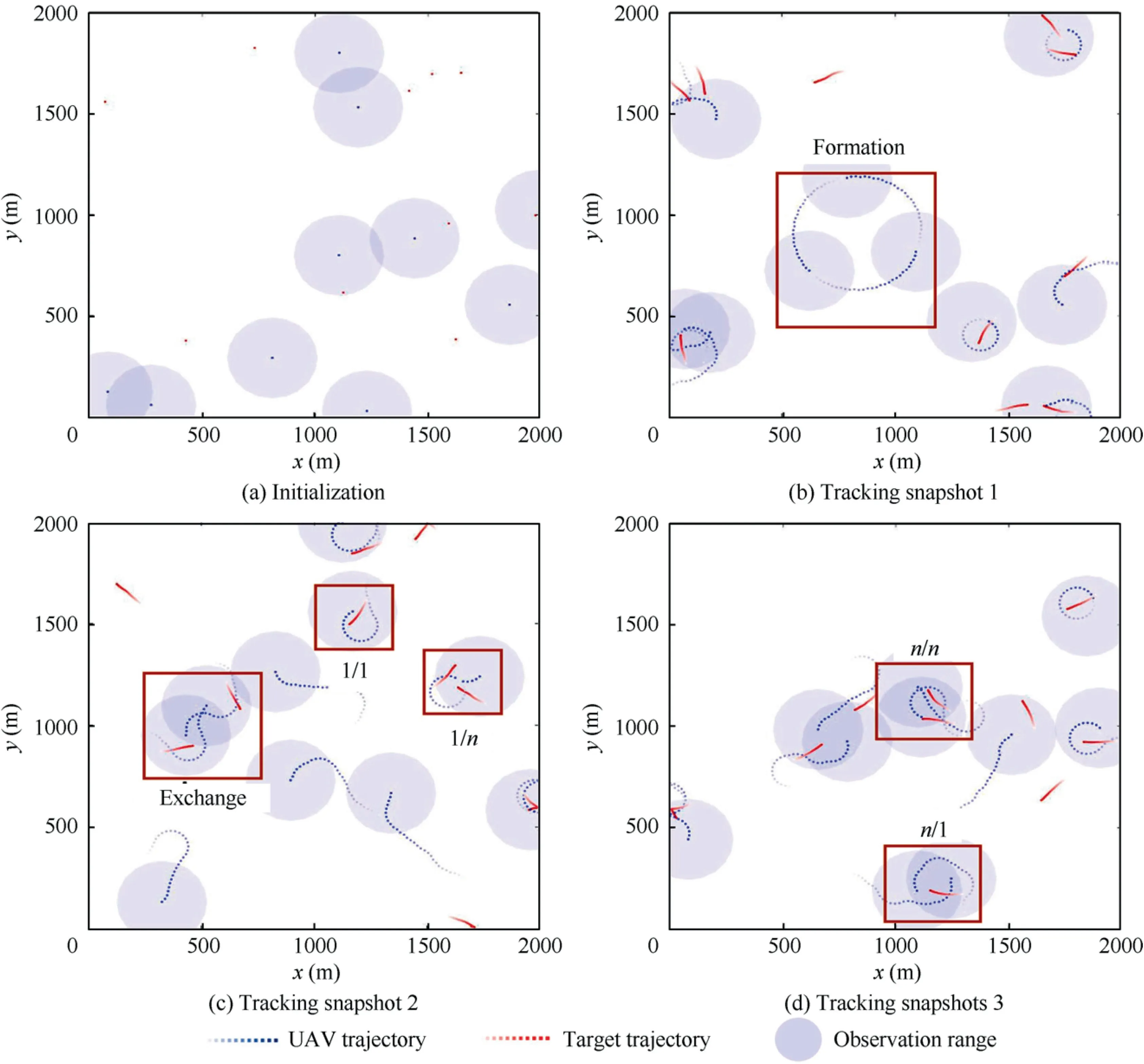
Fig. 5 Visualization of multi-target tracking by UAVs.

Table 5 Statistical indicators of execution results in different scenarios.

Surprisingly, even if there is no explicit formation motivation in reward shaping, the UAVs in the red box in Fig. 5(b)form a formation.The previous experiments have verified that maximizing reciprocal rewards can encourage the UAVs to actively cooperate, and the cooperation only exists between the neighboring UAVs, so they have the motivation to approach each other. However, when the UAVs get too close,their observation areas may overlap, which is punished in reward shaping.Therefore,there may also be repulsive motives between the UAVs.It can be seen from the figure that only the communication information is valid among the input information of the 3 UAVs, and each UAV moves under the drive of these two motivations. Therefore, each UAV stays away from other UAVs that are trying to approach, while chasing other UAVs that are trying to stay away. When these motivations among the UAVs are balanced with each other, the UAVs form a formation. Therefore, the visualization demonstrates that the UAVs can emerge a variety of flexible cooperation behaviors using the proposed MAAC-R algorithm.

6.4. Scalability test

In the proposed MAAC-R algorithm,each UAV only interacts directly with its neighbors during both training and execution processes.The above experiments are implemented in the same scenario (2 km × 2 km, 10 UAVs, and 10 targets). Next, we verify the scalability of the previously learned policies in different scenarios.Similarly,the saved actor-networks are reloaded and published to all UAVs for execution.And the learned policies are executed 100 episodes in each scenario. The statistical indicators of the test results are shown in Table 5.

To normalize the tracking performance metrics in different scenarios, the tracking ratio is defined as the proportion of tracked targets to all targets.It can be obtained from the comparison of statistical indicators in all the test scenarios,the performance of MAAC-R is better than the other two methods.This demonstrates that the policy learned using MAAC-R can maintain better generalization ability and scalability in different scenarios. The possible reason is that when calculating the reciprocal reward of each UAV, only those neighboring UAVs that interact directly are considered, which makes the reciprocal reward free from the curse of dimensionality. And,the introduction of PMI can identify those necessary and highly relevant interactions and eliminate unnecessary and weakly relevant interactions. Therefore, the decentralized cooperative policy learned in MAAC-R can be executed well in scenarios where the number of UAVs is larger. Consequently, we believe that the proposed MAAC-R algorithm has the potential to be widely scaled to other collaborative scenarios with more UAVs and targets.

6.5. Computational complexity analysis

There are N homogeneous UAVs and the cardinal number of the individual discrete action space is M. Consider the most extreme case that each UAV can communicate with all other N-1 UAVs. To compute the reciprocal reward for each UAV, its computational complexity is O(N-1) since it only needs to calculate the PMI of N-1 random event pairs.However, if we use the MI to capture the dependence between UAVs’ policies, the computational complexity is O((N-1)M) ; and if we use the social influence model to compute the causal influence of a UAV’s action on other UAVs’ policies, the computational complexity is O(2(N-1)M) when the causal influence is assessed using counterfactual reasoning.Moreover,both MI and social influence are aggregate statistics between random variables, and their calculation requires knowing or estimating the action policies of other UAVs. Therefore, these are much more complicated than directly calculating PMI.

7. Conclusions

This work studies the MTTG problem for UAV swarms in an unknown environment using the MADRL technique.We propose the maximum reciprocal reward method to enable largescale homogeneous UAVs to learn cooperative policies in a decentralized manner. Specifically, the reciprocal reward of each UAV is defined as the dot product of the environment reward vector of all neighboring UAVs and the dependency vector between the UAV and its neighbors, where the dependence can be estimated using a PMI neural network. Further,the reciprocal reward is used as a regularization term to reshape the UAV’s original reward. Maximizing the reshaped reward can not only maximize the UAV’s reward but also maximize the rewards of the neighboring UAVs,which realizes decentralized cooperation between UAVs. Combined with the maximum reciprocal reward method and PMI estimation, we propose the MAAC-R algorithm based on the experience replay sharing mechanism to learn the collaborative sharing policies for UAV swarms.Numerical experiments demonstrate that the proposed MAAC-R algorithm can better improve the cooperation between UAVs than the baseline algorithms, and excite the UAV swarms to emerge a rich form of cooperative behaviors. Also, the learned policy can well scale to other collaborative scenarios with more UAVs and targets.

Although this paper only focuses on improving the cooperation of homogeneous UAV swarms, in the future, we will adapt the maximum reciprocal reward method to heterogeneous UAV swarms to improve their cooperation in a decentralized manner.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This work was funded by the Science and Technology Innovation 2030-Key Project of ‘‘New Generation Artificial Intelligence”, China (No. 2020AAA0108200) and the National Natural Science Foundation of China (No. 61906209).