Real-time trajectory optimization for powered planetary landings based on analytical shooting equations
Lin CHENG, Peng SHI, Shengping GONG, Zhenbo WANG
a School of Astronautics, Beihang University, Beijing 100191, China
b Department of Mechanical, Aerospace, and Biomedical Engineering, University of Tennessee, Knoxville 37996, USA
KEYWORDS Adaptive homotopy;Analytical solution;Fuel-optimal landings;Indirect method;Real-time control
Abstract Traditionally, numerical trajectory integration for shooting equation calculation and iterations for shooting with randomly guessed initial solutions deteriorate the real-time performance of indirect methods for on-board applications. In this study, the indirect method is improved to achieve real-time trajectory optimization of fuel-optimal powered planetary landings with the help of analytical shooting equation derivations and a practical homotopy technique. Specifically, the contributions of this paper are threefold.First,the analytical expressions for shooting equation calculation are derived to replace the traditional time-consuming trajectory integration.Consequently,the computational efficiency is significantly improved.Second,the original three-dimensional landing problem is connected with a simplified one-dimensional problem that only involves the vertical dynamics, and its analytical solution is obtained based on Pontryagin’s minimum principle. Third,starting with the analytical solution, the accurate solution of the original landing problem can be obtained through an adaptive homotopy process. Simulation results of Earth landing scenarios are given to substantiate the effectiveness of the proposed techniques and illustrate that the developed method can obtain a fuel-optimal landing trajectory in 5 ms with 100% success rate.
1. Introduction
With the increasing demand for reusable launchers on Earth and planetary landings for deep space exploration, real-time and optimal trajectory optimization has become a basic requirement to achieve pinpoint soft landings.In this study,real-time trajectory optimization for fuel-optimal landings is achieved with the help of analytical shooting equation derivations and a practical homotopy technique.
Essentially,the landing problems are optimal control problems that can be resolved by computational optimization methods including indirect methods and direct methods.Based on the first-order optimality principle of functional,indirect methods transform optimal control problems into Two Point Boundary Value Problems (TPBVPs), and resolve them by nonlinear programming methods.However, both the numerical trajectory integration for calculating the shooting condition of TPBVPs and the iteration for finding solutions to match the shooting condition deteriorate the real-time performance of indirect methods and hinder their on-board applications. The recently developed techniques including homotopy,costate normalization,and initial solution supplied by deep neural networkshave significant positive effect on improving the real-time performance and reliability of indirect methods. Meanwhile, benefiting from the development of computer technology in recent decades,direct methods, which discretize the optimal control problems into numerical programming problems through profile parameterization techniques, have attracted generous attention owing to their advantages of acceptable convergence,easy constraint handling, and excellent application generality.Indirect methods including pseudospectraland convex optimization methodshave been widely applied in engineering activities involving entry trajectory optimization.low-thrust trajectory optimization.and landing trajectory optimization.However, to achieve high solving accuracy, a large number of discretization variables are needed, and the corresponding computational time increases severely.
To meet the real-time requirements for real-world implementation, analytical landing guidance methods are preferred and applied.Typical analytical guidance methods include Apollo polynomial guidance and ZEM/ZEV feedback guidance. In 2019, Lu summarized the polynomial guidance methods in the literature and presented a united version which is called Augmented Apollo Powered Descent Guidance(AAPDG).Compared to the computational optimization methods,the analytical guidance methods generate the control commands based on analytical expressions related to real-time flight states, and thus enjoy significant real-time advantage.However, the existing analytical guidance methods possess the following three shortcomings.One is about the fuel consumption. Augmented Apollo descent guidance is not fueloptimal (more likely extended energy-optimal versions), and it has been reported that fuel consumption of fuel-optimal guidance methods can be saved by tens of percent over the Apollo descent guidance.Second,the Apollo descent guidance design does not take into account the hard bounds on the thrust magnitude. Finally, Apollo descent guidance solution requires an offline determined time of flight.The optimal flight time is not easy to determine onboard.
In this study,the advantages of computational optimization methods and analytical methods are combined, and real-time fuel-optimal trajectory optimization based on indirect methods is achieved based on analytical shooting equation derivations and a practical homotopy technique. To overcome the issues of numerical trajectory integration and iterations for solution search that deteriorate the real-time performance of indirect methods,three contributions are emphasized in this study.First,the expressions of trajectory integral for differential equations of states and costates are derived, and the shooting condition is analytically calculated. Consequently, the time-consuming trajectory numerical integration is avoided, and the computational efficiency is significantly improved. Second, the original three-dimensional landing problem is connected with a simplified one-dimensional problem which only considers the vertical dynamics,and its analytical solution is obtained based on Pontryagin’s minimum principle.Third,starting with the analytical solution,the accurate solution of the original landing problem is obtained through an adaptive homotopy process.The introduction of the homotopy technique helps to avoid the initial solution guessing and to achieve a 100% convergence, which further improve the real-time performance and the reliability of the algorithm.
The rest of this paper is organized as follows. The considered landing problem is introduced, and its solution based on Pontryagin’s minimum principle is provided in Section 2.In Section 3, the analytical expressions for shooting equation calculation with an arbitrary costate vector are derived.In Section 4,the analytical solution of the simplified vertical landing problem is obtained, and on this basis, an adaptive homotopy algorithm is developed to achieve the accurate solution of the original landing problem. Simulation results are given in Section 5 to evaluate the effectiveness of the proposed techniques,and the study is summarized in Section 6.
2. Problem formulation and solution
2.1. Problem formulation
In this study we focus on the real-time trajectory optimization of fuel-optimal powered planetary landings over a planet.The corresponding three-dimensional point-mass descent dynamics in an inertial Cartesian coordinate system is expressed as

2.2. Optimal solution
The considered powered landing problem is a typical optimal control problem that can be solved by the indirect method.Originated from Pontryagin’s minimum principle, the indirect method transforms the original optimal control problem into a TPBVP. Here, a summary of the method is provided for convenience and completeness.
Based on Pontryagin’s minimum principle, the Hamiltonian function H is defined as

where Φ(z) is called shooting function and z=[λ(t),t] is the to-be-determined shooting vector. This is a TPBVP, and a number of off-the-shelf numerical root-finding methods exist to find the optimal solution z=[λ(t),t] that satisfies the shooting condition Φ(z)=0.
However,there are two issues that deteriorate the real-time performance of the algorithm for quickly finding the optimal solution z=[λ(t),t].First,the numerical integration of the differential equations from tto tis time-consuming when high-quality trajectory is required.Second,the TPBVP is essentially a nonlinear problem,and when the initial solution z is not appropriately initialized, the convergence of the existing rootfinding methods cannot be guaranteed. Thus, one successful solution may need multiple shooting iterations. To overcome the above two issues,we analytically derive the shooting equation Φ(z) in this study, and consequently the time-consuming trajectory integration is not required. Then, a practical homotopy technique is presented to guarantee successful shooting with a 100%convergence. Consequently, the real-time performance and reliability of the algorithm are further improved.The technical details are given in the following sections.
3. Analytical shooting equations
In this section, we focus on the analytical calculation of the shooting equation when an arbitrary solution z=[λ(t),t] is given.
3.1. Analytical optimal control
First, analytical control for fuel-optimal landings is determined. According to Eqs. (9) and (10), the costates can be expressed as

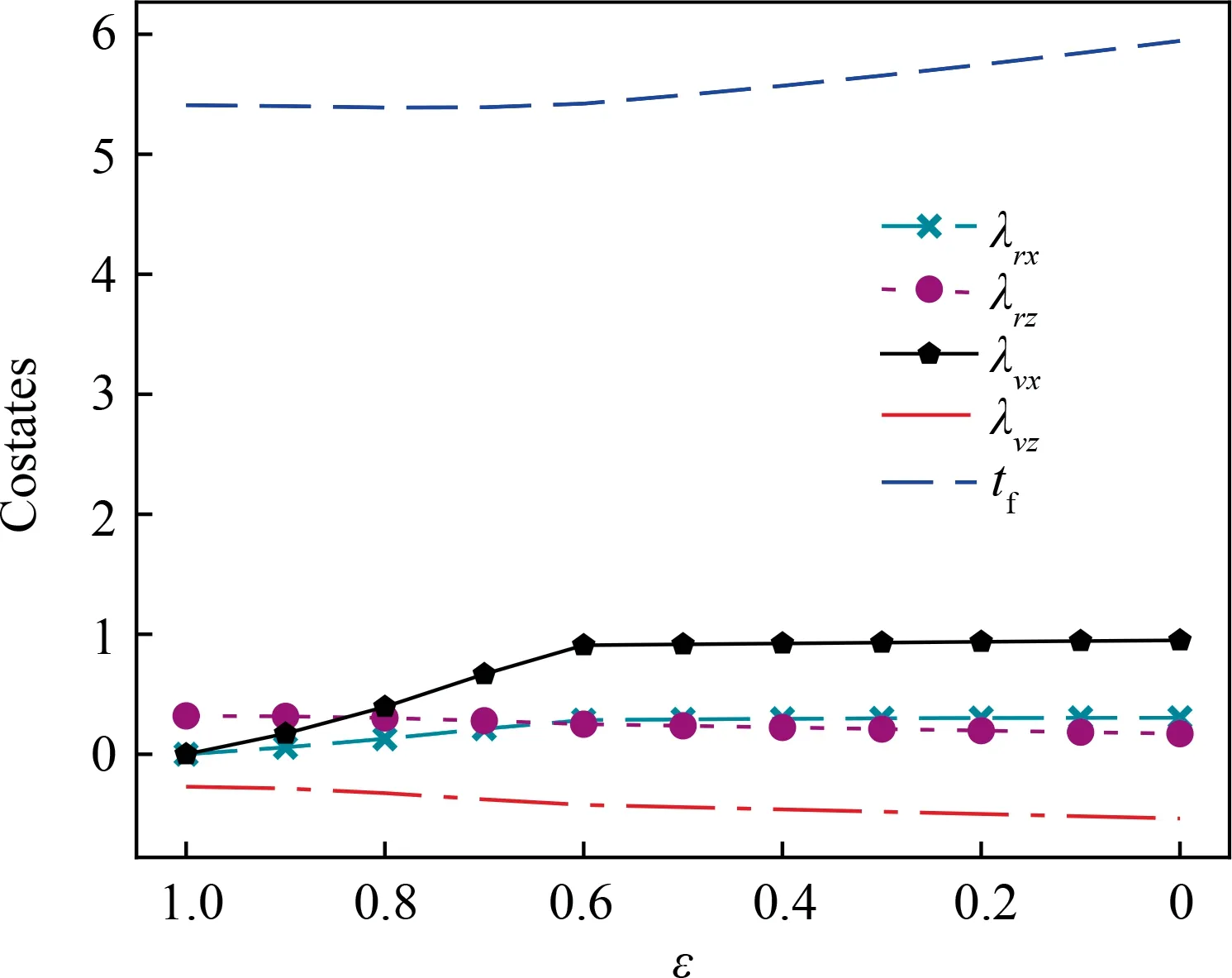
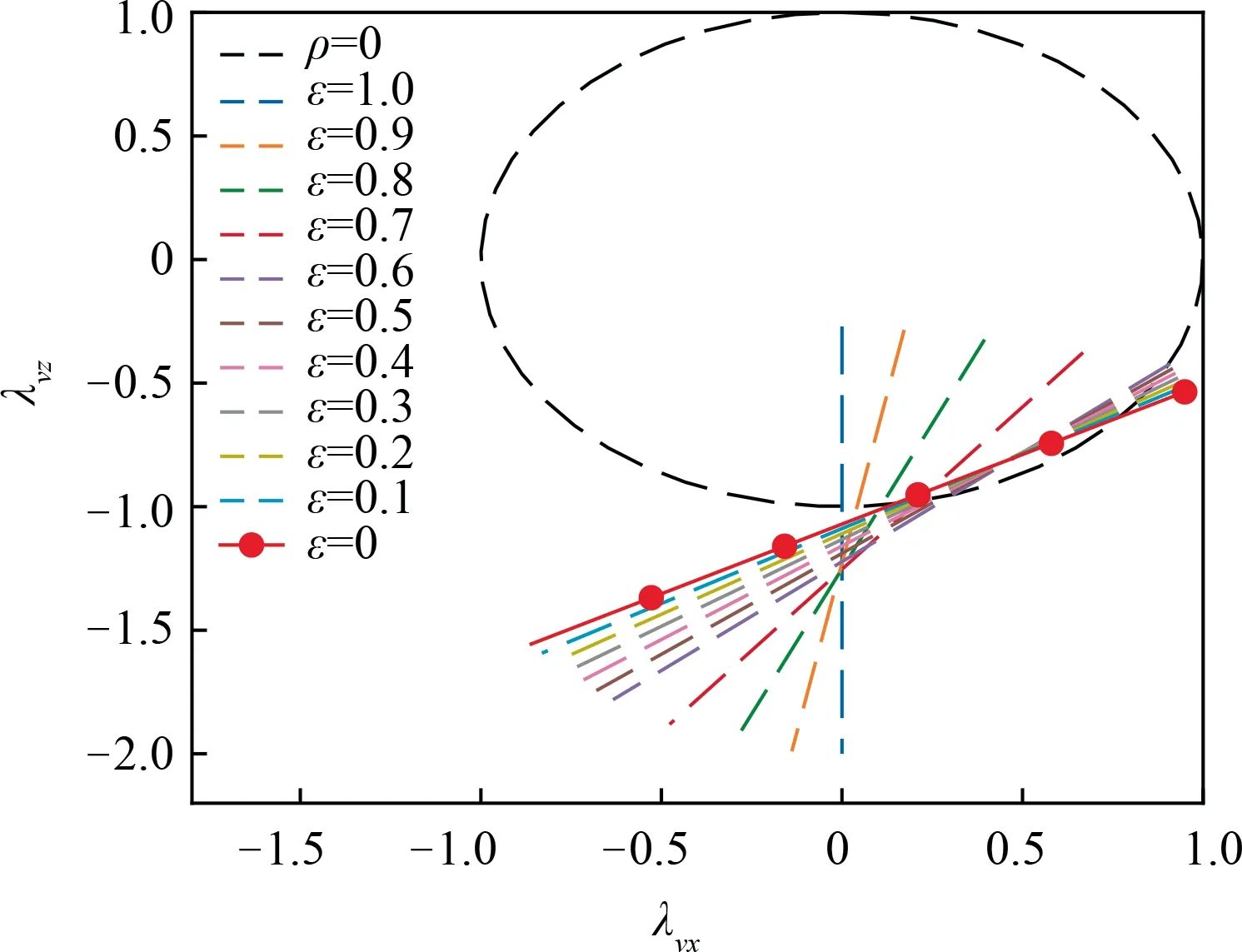
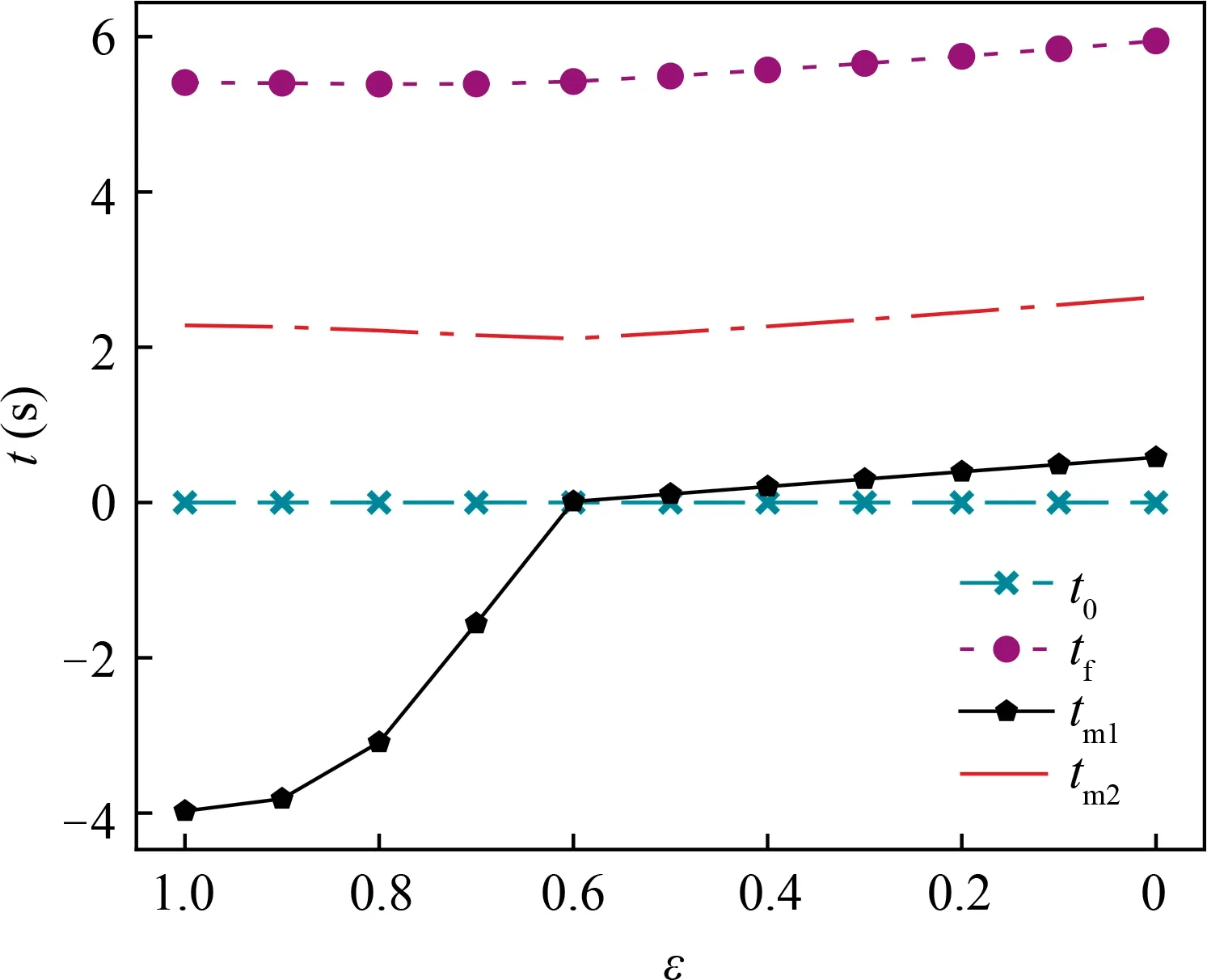
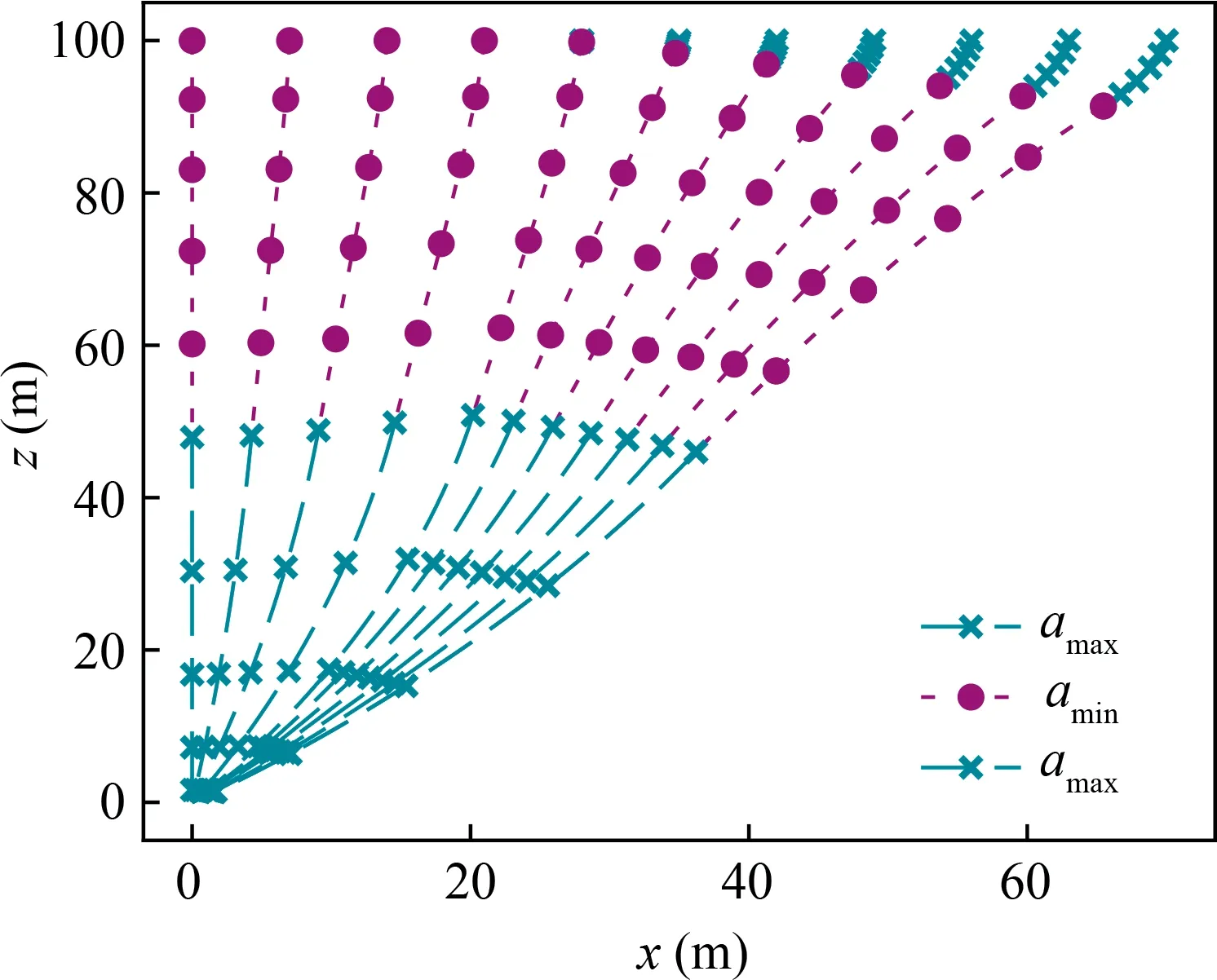
(B) If t (C) If t (D) If t (E) If t At this point, the analytical control laws for the acceleration amplitude and direction are obtained, which are fundamental to achieve the analytical calculation of shooting equation in the subsection. Based on the above obtained analytical acceleration control,we focus on the analytical calculation of shooting equations in this subsection. First, we derive the analytical expression of velocity driven by a constant acceleration amplitude in one phase. Specifically, Finally, the analytical expression of shooting equation in Eq. (15) is obtained according to Eqs. (29), (30), and (32).Since the trajectory integration is not included, the real-time performance for the shooting equation calculation is significantly improved.So far,the first issue mentioned in Section 2.2 has been overcome, and the second issue will be addressed in the next section. In this section, the original Three-Dimensional (3D) landing problem is simplified into a One-Dimensional (1D) landing problem where only the vertical dynamics is involved, and the corresponding analytical solution is derived.On this basis,we build the dynamical continuation relationship between the 3D and 1D problems, and a practical homotopy technique is presented to achieve the fast generation of the accurate solution of the 3D problem starting with the analytical solution of the 1D problem. When the lateral motions are not considered,the landing problem is simplified into one 1D problem, and the dynamical model can be rewritten as At this point, we have analytically obtained the costates λ,λand flight times t,tof the vertical landing problem.In the next subsection, we will use this solution to solve the original 3D landing problem. Based on the analytical solution of the simplified vertical landing,a practical homotopy algorithm is presented in this subsection to achieve fast and reliable generation of accurate solutions of the 3D landing problem. The detailed homotopy process is summarized in Algorithm 1. Algorithm 1. Analytical homotopy algorithm.1. Mark the original 3D initial state as X0 =[r(t0),v(t0)] and target terminal state as Xf =[rf,vf],and extract the corresponding vertical states [rz0,vz0,rzf,vzf]. According to Eqs. (43), (48), and(49), the solution λrz0, λvz0, tf can be analytically obtained.2. Define X1 =[0,0,rz0,0,0,vz0]. According to the Pontryagin’s minimum principle, the solution λ1 =[0,0,λrz0,0,0,λrz0,tf]satisfies the shooting condition in Eq. (15) and is the solution of the 3D landing problem with initial state X1.3.Define homotopy state Xε =(1-ε)X0+εX1,and initialize the corresponding homotopy costate λε =λ1. Define homotopy coefficient ε, and initialize its initial value as 1 and correction stepsize Δε=1.4. Correct ε=ε-Δε, and update Xε =(1-ε)∙X0+ε ∙X1.5. Start with the current costate λε, and obtain the accurate solution of Xε using nonlinear root-finding methods. The shooting equations in Eq. (15) are analytically calculated according to the derived Eqs. (29), (30), and (32).6. if Φ(z)==0 then 7. if ε==0 then 8. Jump to Line 18.9. else 10. if The shooting condition is satisfied twice in succession then 11. Δε=2Δε.12. end if 13. Jump to Line 4.14. end if 15. else 16. Restore ε=ε+Δε, correct Δε=Δε/2. Jump to Line 4.17. end if 18. Stop, get the corresponding optimal control and trajectory.Store the results. Finally,the above mentioned two issues that deteriorate the real-time performance of the algorithm have been well addressed. Specifically, the analytical derivation of shooting equations proposed in Section 3 helps to avoid the timeconsuming trajectory numerical integration. Meanwhile, the homotopy technique proposed in this Section 4 starts the solving with an analytical solution, and can potentially achieve 100% convergence that further improves the real-time performance and enhances the reliability of the algorithm.The initial homotopy stepsize Δε is set to be 1, which enables the algorithm to complete the homotopy as soon as possible whenthe solution of the 1D problem is near to the optimal solution of the 3D one.Simulation results will be given in the next section to validate the effectiveness of the presented techniques. Table 1 Parameter settings. In this section, simulations are conducted to evaluate the proposed techniques. The algorithms are implemented in Python 3.7 on a desktop with Inter Core i9-10850 CPU @3.60 GHz RAM 32.00 GB and operating system of Windows 10. Modified Powell methods (MINIPACK’s hybrd and hybrj routines)are adopted to search the solutions with an absolute tolerance |Φ(z)|<10in this work. Other parameters are set as displayed in Table 1. First, we focus on the real-time performance of the proposed algorithm, which is especially emphasized in this study. The real-time performance improvement of the proposed algorithm is credited to two factors: one is the analytical calculation for shooting equations, and the other is the developed analytical homotopy. Here, we compare the time consumption and accuracy of single calculation for shooting equations by the proposed analytical method and traditional integral methods.The trajectory integral is conducted using the fourth-order Runge–Kutta method. Of course, in different hardware and software conditions, the specific values may be different;however,we compare the results under the same simulation condition,and we believe the relative comparison is still of reference significance. Table 2 displays the results. Since Runge–Kutta method is a numerical method,which has inevitable numerical errors, Table 2 also includes the statistics about the norm of terminal position and velocity error vectors. MAE refers to the mean absolute error, and MSE refers to the mean square error. As we can see from the table, the proposed analytical method has significant computational advantage. Meanwhile,the whole derivation for analytical expression of shooting equations does not involve any simplification, thus the analytical results have no loss on accuracy. On the other hand, the fourth-order Runge–Kutta method achieve a poor real-time performance when a high-quality trajectory integral is required. By increasing the stepsize, the computational speed for shooting equation calculation can be improved, but the accuracy deterioration is obvious. How to balance the realtime performance and accuracy is one difficulty for the traditional trajectory integration method, but the proposed analytical method of this study has no such concern. Meanwhile,we also compare different methods for one successful solution of the 3D landing problem,and the results are displayed in Table 3. The compared methods include the presented method using the analytical shooting calculation and homotopy techniques, the method using analytical shooting calculation and random guessed initial solution,and the traditional method using trajectory integral and random guessed initial solution. We can draw the following three conclusions from this table. First, benefiting from the analytical shooting calculation, the proposed algorithm has a significant realtime performance compared with the method that adopts numerical integral methods.Second,the homotopy techniques help achieve a 100%success rate and enhance the reliability of the algorithm. Third, increasing the stepsize of the Runge–Kutta method can improve the computational speed, but the converge deteriorates severely. The reason is that a too large stepsize reduces the accuracy of trajectory integration for shooting equation calculation as well as the gradient stability for solution adjustment during the root-finding, and thus degrades the convergence. Table 2 Single calculation for shooting equations. Table 3 Comparison for one successful solution. Fig. 1 Costate histories during homotopy. Fig. 2 λv(t)=-λr(t0)∙t+λv(t0) during homotopy. Fig. 3 Time histories during homotopy. Fig. 4 Position histories during homotopy. In this subsection,we turn our attention to the homotopy process.Figs.1–4 graphically demonstrate the specific details during homotopy. For illustration, the states are initialized as r(t)=[70,0,100] m,v(t)=[-3,-0,-15] m/s, and the target landing states are chosen as r=[0,0,0]m,v=[0,0,0]m/s.In Algorithm 1,an adaptive homotopy technique is developed to automatically adjust the homotopy stepsize Δε, however in Figs. 1–4, we manually choose much denser homotopy coefficient ε with the purpose of illustrating more homotopy details.The algorithm starts from ε=1,which corresponds to the simplified vertical landing problem, and ends with ε=0, which corresponds to the original 3D landing problem.The following four conclusions can be drawn from the figures. First, according to Fig.1,there exists continuation relationship between the solutions of different ε. Based on this point, an analytical and adaptive homotopy technique is presented,which helps avoiding traditional initial solution guessing.Consequently,the convergence and reliability of the proposed algorithm are enhanced. Second, as displayed in Fig. 2, the costate λ(t) linearly changes along with the time.Combined with Eq.(13),the switching function ρ is determined by λ(t).According to Eqs.(21)and(22),the switching times tand tare further determined.Third,the intersection between the switching condition ρ=0 and λ(t)of Fig.2,or the relative sizes of t,t,t,tof Fig.3 can be used to determine the flight profile of the optimal acceleration amplitude a. Fourth, as displayed in Fig. 4, with the increase of lateral distance/velocity, a flight phase with maximum acceleration amplitude is added in early flight stage with the aim to eliminate the lateral motion. Meanwhile,regardless of the initial state difference, the proposed algorithm can quickly find the optimal control and accurately drive the lander to the target landing site. Fig. 5 Position histories in typical landing mission. Fig. 6 Velocity histories in typical landing mission. Fig. 7 Control histories in typical landing mission. Fig. 8 3D trajectories in multiple landing missions. Additionally, the solution optimality of the proposed method is analyzed in this subSection 100 flight missions with randomly determined initial state are conducted, and their solutions are obtained by a regular method using analytical shooting calculation and randomly guessed initial solution.For each flight scenario, 10 repeated calculations are conducted.Through analyzing the obtained results,we do not find the case of multiple local optima. The reason might lie in that compared with other complex optimal control problems, the dynamics of the planetary landing problem are nearly linear,and consequently less vulnerable to fall into multiple local optima. Furthermore, these solutions are all identical with the solutions of the proposed analytical method. As such,the solution optimality of the proposed method can be guaranteed to some extent. Finally, the optimized results by the proposed algorithm are provided. Figs. 5–7 demonstrate the position, velocity, and control histories of a typical landing mission, wherein the initial states are randomly chosen as r(t)=[50,5,100]m,v(t)=[-3,-1,-15] m/s, and the target landing states are chosen as r=[0,0,0] m,v=[0∙0,0∙0,0∙0] m/s. We can see from the figures that the proposed algorithm can find the optimal control that drives the lander to the target landing site.Meanwhile, Fig. 8 displays 100 trajectories randomly initialized according to Table 1.We can find that the landing control system adopts a Three-Phase a-a-ascheme when the initial states have large lateral deviations. Meanwhile, the control system adopts a Two-Phase a-ascheme for optimal landings when the lander has small lateral deviations. In this study, the indirect method is improved to achieve realtime trajectory optimization of planetary fuel-optimal landings. Traditionally, numerical trajectory integration and iterations for shooting with randomly guessed initial solutions deteriorate the real-time performance of the indirect method.To overcome these two obstacles, analytical expressions for shooting equation calculation are obtained in this paper and,consequently, the time-consuming trajectory numerical integration is not required. On this basis, the analytical solution of a simplified landing problem that only involves the vertical dynamics is obtained, and a practical homotopy technique is developed to achieve the fast generation of the solution of the original problem starting with the obtained analytical solution. Simulations of Earth landing scenarios are performed to substantiate the effectiveness of the proposed techniques and results illustrate that the developed method can obtain a fuel-optimal landing trajectory in 5 ms with 100%convergence. The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. This work was supported by the National Natural Science Foundation of China (Nos. 11872223, 11902174, and 11772167).3.2. Analytical calculation of shooting equation


4. Analytical homotopy
4.1. Analytical solution of vertical landing


4.2. Homotopy algorithm


5. Simulation and results
5.1. Real-time performance


5.2. Homotopy process
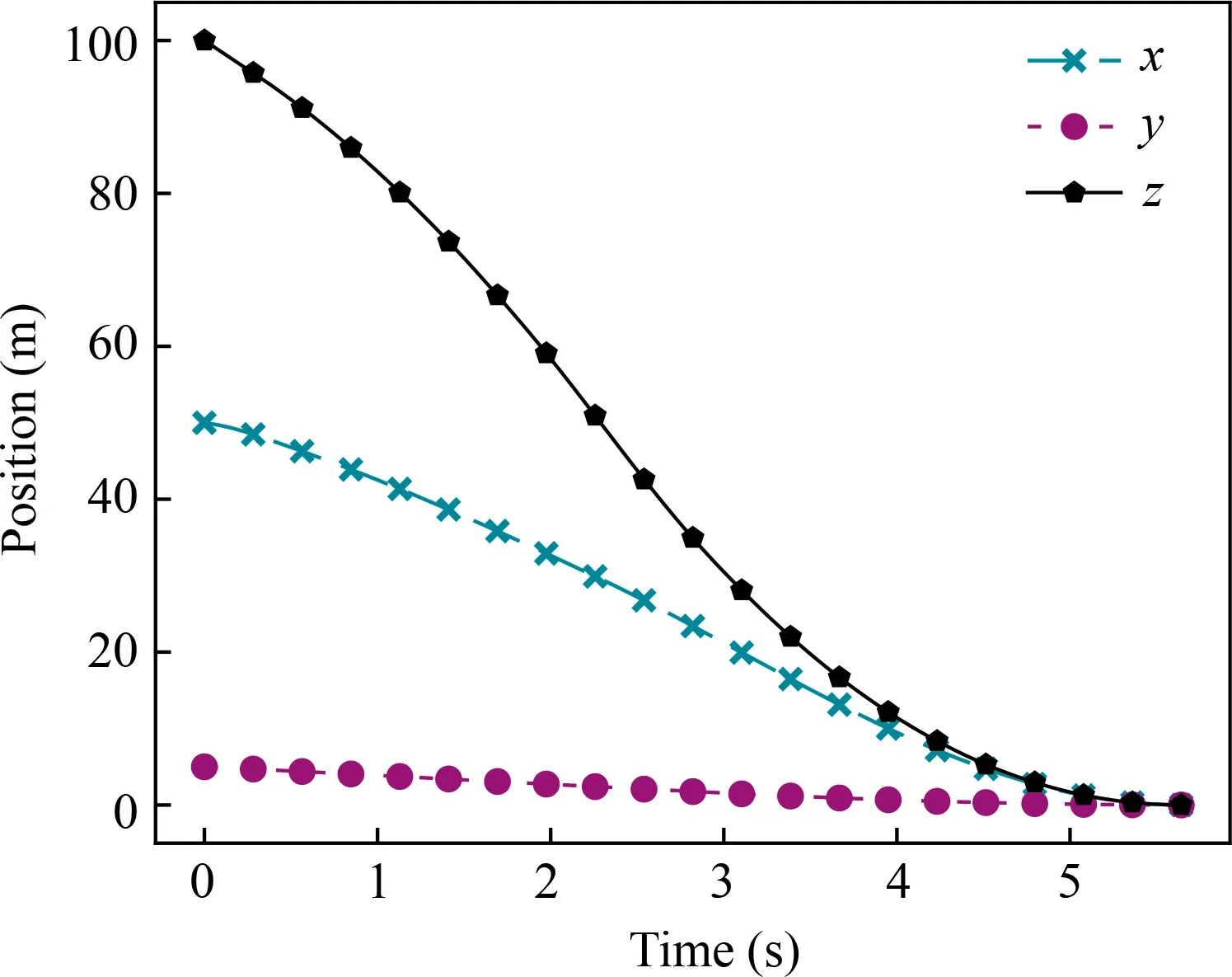
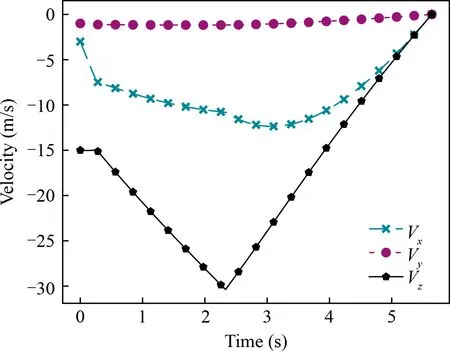
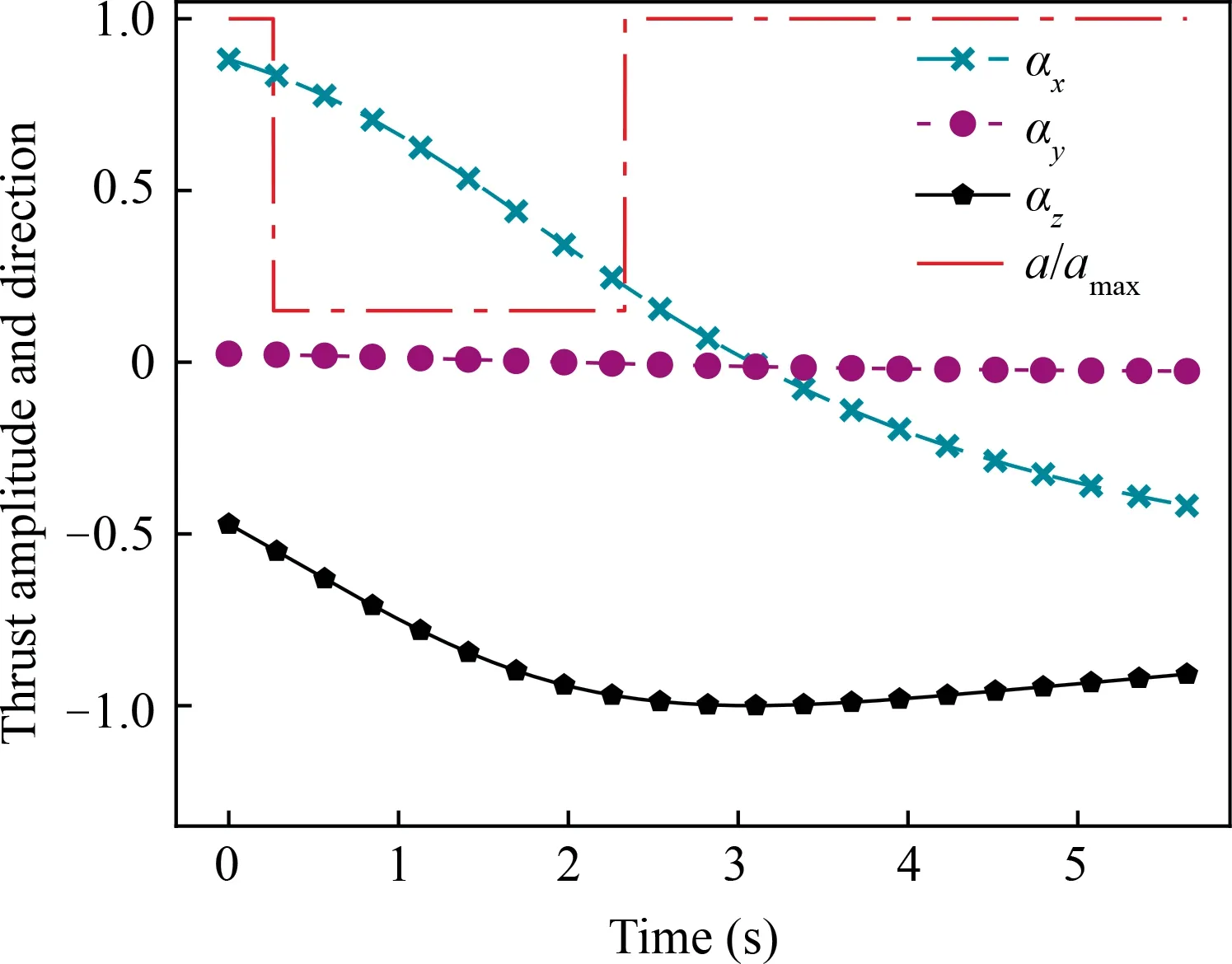

5.3. Typical landing scenarios
6. Conclusions
 Chinese Journal of Aeronautics2022年7期
Chinese Journal of Aeronautics2022年7期
