Integrated guidance and control for damping augmented system via convex optimization

Bong-Gyun PARK, Tae-Hun KIM

The 1st R&D Institute-4, Agency for Defense Development, Daejeon 34186, Republic of Korea

KEYWORDS Convex optimization;Damping augmented system;Integrated guidance and control;Physical constraint;Primal-dual interior point method

Abstract In this paper, an integrated guidance and control approach is presented to improve the performance of the missile interception. The approach includes damping augmented system with attitude rate feedback to decrease the oscillation during the homing phase for missiles with low damping.In addition,physical constraints,which can affect the performance of the missile interception,such as acceleration limit, seeker’s look angle,and look angle rate constraints are considered.The integrated guidance and control problem is formulated as a convex quadratic optimization problem with equality and inequality constraints, and the solution is obtained by a primal–dual interior point method.The performance of the proposed method is verified through several numerical examples.

1. Introduction

Conventional approaches to design the inner-loop autopilot and the outer-loop guidance are based on spectral separation assumption. As the rapid change of the engagement geometry between the high-speed missile and target occurs during the homing phase, the spectral separation, which implies that the missile dynamics for the autopilot is much faster than the kinematics for the guidance,will not hold until the interception and cause the degradation of the guidance performance. The integrated guidance and control approach can be used to deal with this drawback of the conventional approach and to improve the performance of the homing phase. In addition, to satisfy the requirement of the specific mission and to overcome the limited capability of the missile, the various constraints such as impact angle, impact time, and look angle limit could be considered to design the guidance and control laws.Especially,physical constraints of the seeker are very critical to achieve the guidance mission because the accurate and valid target information is needed to generate the control commands throughout the homing phase and to enhance the capturability against fast moving targets.

A lot of studies of the integrated guidance and control have been conducted based on several nonlinear control and optimal control methods.In Ref.1,the nonlinear integrated guidance and control system was linearized by the feedback linearization, and then the command was generated by the Linear Quadratic Regulator (LQR) technique. A slidingmode control method was applied to design the integrated guidance and control loop, and a sliding surface based on the zero-effort miss was used in Ref. 2. The sliding mode controland the higher-order sliding mode controlwere also applied to develop the integrated guidance and control for dual-control missiles. In Ref. 5, the sliding mode control approach was used to design the control law for the integrated guidance and control system against ground fixed targets with a desired impact angle.In Ref.6,θ-D method as a suboptimal control method was employed to develop the integrated guidance and control algorithm, and it did not have iterative solutions. A numerical approach to solve the integrated guidance and control problem of a moving-mass-actuated missile was applied based on state-dependent Riccati equations methodology in Ref. 7. In Ref. 8, the integrated guidance and control design method was proposed based on the adaptive block dynamic surface control approach to avoid the repeated differentiations of the virtual controls.In Ref.9,the integrated guidance and control problem under the terminal angle of attack,impact angle, and miss distance constraints was defined as the discrete-time finite horizon quadratic optimization problem, and the solution was explicitly obtained as a timevarying state feedback controller.

Recently,studies of the guidance and control problem with the seeker’s constraints have been conducted. In Ref. 10, the bias-shaping method for Biased Proportional Navigation(BPN) was developed to control the look angle and impact angle. Optimal solutions to a guidance problem with impact angle and seeker’s look angle limits were obtained using the optimal control theory with a state variable inequality constraint in Ref.11.A guidance law with a time-varying proportional navigation gain was developed for satisfying various physical constraints such as look angle constraint and lateral acceleration limit,and the gain was numerically given by solving a second-order cone programming problem in Ref.12.In a three-dimensional engagement scenario, the impact time control guidance problem with seeker’s filed-of-view constraint was solved based on BPN, and the optimality of the biased feedback term was discussed in Ref. 13. However, a real seeker’s look angle should be defined based on the missile’s body longitudinal axis,but not velocity direction axis.Above literatures of Refs.10–13 dealt with the seeker’s look angle using the lead angle defined from the missile’s velocity direction axis,which means that the above-mentioned approaches could not control the real seeker’s physical constraints. Hence, the missile attitude dynamics should be also considered to more accurately handle the seeker’s look angle. In Refs. 14,15, the integrated guidance and control problem with seeker’s fieldof-view limits was studied, which can control the real seeker look angle constraint. A three-dimensional integrated guidance and control problem for missiles with strap-down seeker’s field-of-view constraint was investigated, and the solution was obtained using dynamic surface control approach with integral barrier Lyapunov function in Ref. 14. The authors of Ref. 15 solved the integrated guidance and control problem with the seeker’s look angle and look angle rate limits via convex optimization.

As the missile airframe has generally low damping, the oscillation may appear if an additional controller for increasing the damping is not applied to the missile control.If the oscillation occurs in the missile system with low damping during the homing phase,it takes a lot of time to reduce the oscillation and then causes the adverse effect of the seeker with the lower quality of measurements to track the target, thereby decreasing the performance of the guidance and control system. The above-mentioned integrated guidance and control problems did not directly handle the damping of the missile dynamics. Therefore, during the homing phase, the solutions of the previous works might retain the oscillation of the missile and diminish the performance of the interception.

In this paper, we focus on developing the method for the integrated guidance and control of missiles with low damping.The first contribution is to present the approach to apply a damping augmented system, which uses directly the attitude rate feedback,to the integrated guidance and control problem.Compared with the previous works not using a damping augmented system, we could improve the missile interception performance by reducing the oscillation and obtaining the target information from the seeker more robustly. In addition, if the missile is unstable,we could more stably control it to intercept the target by selecting the control gain properly. In the integrated guidance control problems, the proposed approach might be the first time to the best of the author’s knowledge.

The second contribution of this paper is to solve the integrated guidance and control problem for a damping augmented system with various physical constraints as a convex quadratic optimization problem. The equality constraint is defined by discretized equations of the damping augmented system of the missile. In addition, the inequality constrains include the seeker’s look angle, look angle rate, and acceleration limits. As the target should remain within the seeker’s field-of-view during the homing phase to generate the target information,the seeker’s look angle limit is critical constraint.The look angle rate constraint should be also considered to prevent the adverse effect of image blurring that can result in seeker lock-on failure.The acceleration limit is an important constraint because it can cause large miss-distance if the acceleration is saturated near the target.The solution of the formulated problem is obtained by a primal–dual interior point method,which is one of efficient methods to obtain the optimal control solution, and the performance of the proposed method is investigated by the numerical optimization and closed-loop simulations with various conditions.

The remainder of the paper is organized as follows: In the next section, the integrated guidance and control problem for the damping augmented system with equality and inequality constraints is defined as a convex quadratic form.Then,the primal–dual interior point method,which is one of the popular algorithms for the convex optimization, is summarized to obtain the optimal control solution. The various numerical examples are involved to investigate the performance of the proposed integrated guidance and control algorithm in the later section. The final section presents the concluding remarks.

2. Integrated guidance and control problem

In this section,a kinematics between the missile and the target is first defined from the engagement geometry, and then the missile dynamics and physical constraints are defined. Next,the damping augmented system is derived to decrease the oscillation for missiles with low damping. Finally, the integrated guidance and control problem is formulated as a convex quadratic optimization problem with equality and inequality constraints. We assume that all information to generate the guidance and control command can be perfectly obtained,and that the missile is equipped with an imaging seeker.

2.1. Problem formulation

Consider the two-dimensional engagement geometry as shown in Fig. 1. The notation of X-Zis the inertial frame and X-Zis the reference frame,which is defined by the initial missile body angle θ, and x-zis the missile body-fixed coordinate frame. The subscripts M and T denote the missile and the target, respectively. The notations of γ, V, and a are the flight path angle,the constant speed,and the normal acceleration, respectively, and the target is assumed to be nonmaneuvering. In addition, z is the lateral relative range between the missile and the target in the reference frame.The various angles are described in Fig. 2, and the positive angles are defined as a counterclockwise rotation. Here, ε, α,and λ, present the look angle, the angle of attack, and the line-of-sight, respectively.

The linearized kinematics and dynamics should be required to formulate a convex optimization problem of the integrated guidance and control. If the missile and the target fly close to the collision course and the line of sight is small during the homing phase (i.e., near head-on case), we can obtain the linearized equations of motion using the small angle approximation. In this study, we choose the reference frame around the initial attitude angle to linearize the kinematics and dynamics because the optimization solution can be directly applied to the actuator control command without any transformation to the body frame when the optimization is performed for every guidance and control cycle, thereby decreasing the computational time for the real time application.

To express the kinematics between the missile and the target, the Zero-Effort-Miss (ZEM) is first defined as

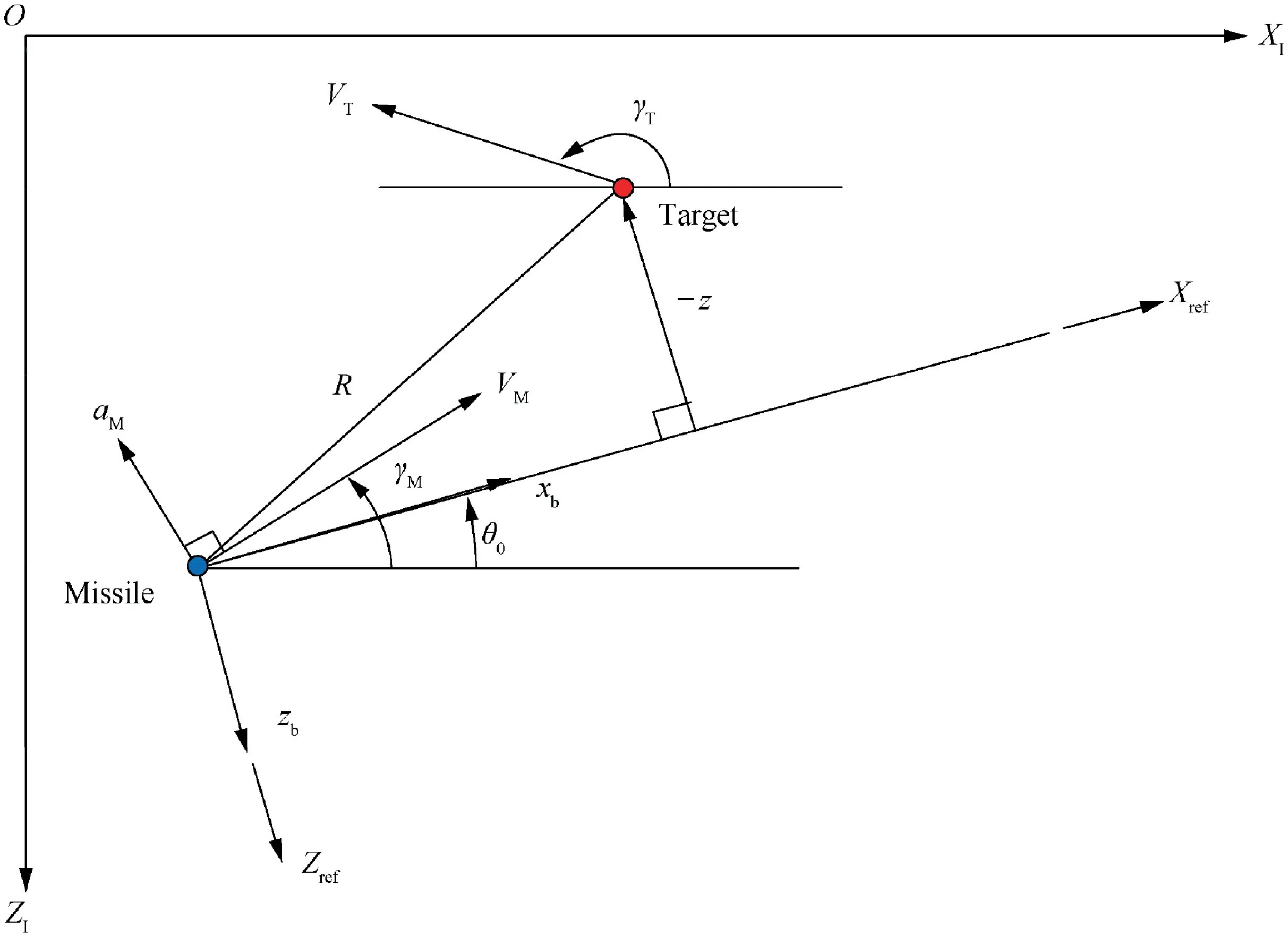
Fig. 1 Two-dimensional engagement geometry.

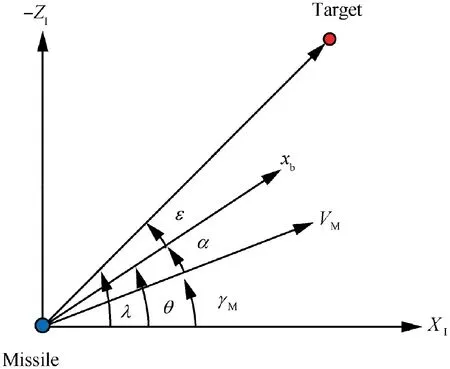
Fig. 2 Two-dimensional definitions of the positive angles.

2.2. Damping augmented system

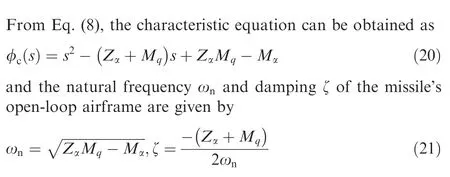
From Eq. (21), the missile damping might be very small because the dimensional derivative of the pitch damping moment,M,is generally not large,and the missile against fast moving targets would be designed to enhance the agility by means of the low M. This causes the missile oscillations during the homing phase if the control system to increase the damping is not considered, which can affect the missile interception performance. Therefore, in this paper, to increase the missile damping by utilizing the pitch rate feedback of the missile, the damping augmented system is derived as follows:

2.3. Convex optimization problem

To solve the integrated guidance and control problem by convex optimization, the above formulated continuous system dynamics for the damping augmented model should be first discretized as follows:

3. Primal-dual interior point method

A primal–dual interior point method, which is a popular and efficient method as one of the algorithms for solving convex optimization problems, is used to obtain solutions to the integrated guidance and control problem defined in Eq. (40). In this section, we summarize the primal–dual interior point method.

4. Numerical examples

4.1. Basic property without inequality constraint

This subsection presents the basic properties of the proposed method. In the first case, the inequality constraints are not considered to check the effect of K. The control gain is set to K=0, 0∙02, 0∙05. The numerical optimization results are shown in Fig. 3(a)-3(e). As presented in the angle of attack,pitch rate,and look angle figures,the oscillation highly occurs during the homing phase when K=0 because the missile airframe has very low damping.However,if the control gain Kis set to have the proper damping of the missile,the oscillation is decreased during the engagement.The ZEM is zero at the final time, and the control input changes linearly to zero. From these results,it can be known that the missile intercepts the target more stably by selecting the proper K.

4.2. Basic property with inequality constraint

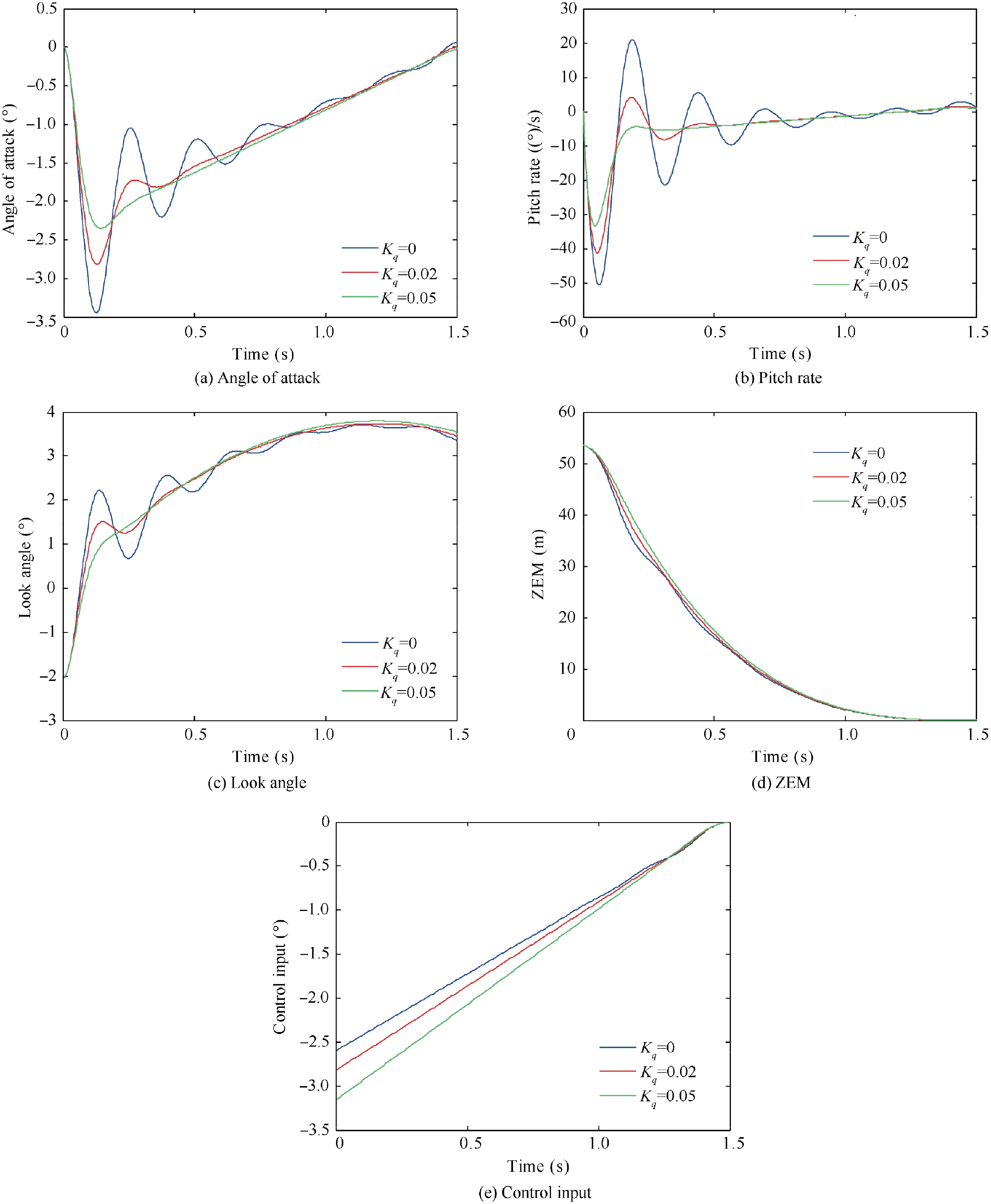
Fig. 3 Numerical optimization results without inequality constraints.

This subsection presents the numerical optimization results with the inequality constraints as shown in Fig. 4(a)-4(g).Compared with the previous case excluding the inequality constraint, the oscillation seems to be small because the acceleration and look angle rate are limited at the beginning of the flight. The look angle, look angle rate, and acceleration stay within their limits. The ZEM converges to zero, and the control input changes linearly after the saturation of the look angle rate and acceleration. The results show that the missile successfully intercepts the target without violation of the constraints through the proposed approach.

4.3. Closed-loop simulation

This subsection presents closed-loop simulations with various initial conditions for practical implementation.The initial conditions are randomly generated for 100 sample runs. The convex optimization runs at the guidance and control computation cycle in order that the initial input obtained by solving the proposed convex optimization problem is used as the control command. In the closed-loop simulation, we do not need a lot of the length of the finite horizon N when the time-to-go is small. Therefore, N is set as follows:

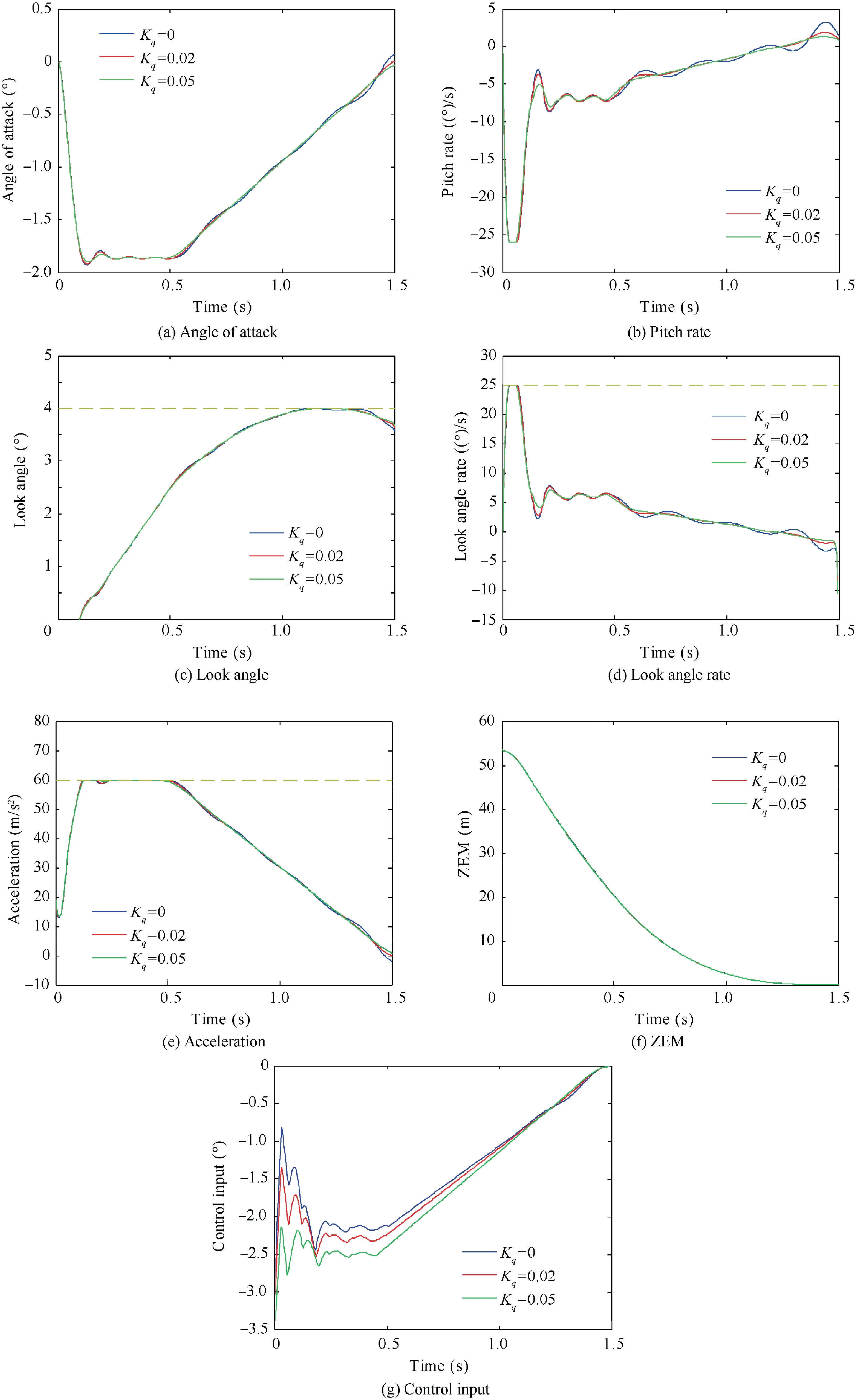
Fig. 4 Numerical optimization results with inequality constraints.

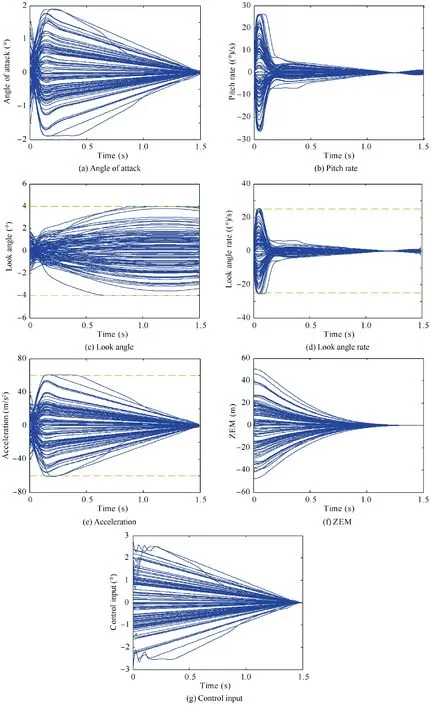
Fig. 5 Closed-loop simulation results for various initial conditions.

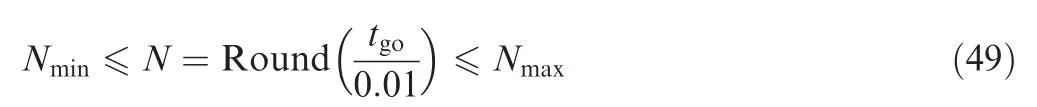
where Round function is to find the nearest integers. In addition, N=2 and N=100 for this simulation case, and these values can be changed as the optimization condition.In the real engagement environment, the measurements obtained from sensors,mounted on the missile,such as the seeker and the Inertial Measurement Unit (IMU) include several noises, and the numerical errors of the optimization can appear while generating the control commands. Therefore,the values of a,ε,and ˙εshould be conservatively chosen considering the margin values.

The angle of attack and the pitch rate are shown in Fig. 5(a)-5(b). The look angle, look angle rate, acceleration constraints are satisfied for all cases, as shown in Fig. 5(c)-5(e). Fig. 5(f)-5(g) shows that the missile successfully intercepts the target by the control input generated from the proposed optimization approach for every guidance and control cycle.The results show that the proposed approach could be utilized for the real-time application.

5. Conclusions

An integrated guidance and control method with physical constraints on the maneuver acceleration, the look angle, and the look angle rate was presented. The attitude rate feedback was also considered to reduce the oscillation, which can appear during the homing phase, for missiles with low damping.The problem presented here was formulated as a convex quadratic optimization problem with equality and inequality constraints. The solution of the formulated problem was obtained by a primal–dual interior point method and could be used as the control command for the real-time application if the problem is solved for every guidance and control computation cycle. The performance of the proposed approach was investigated by the numerical optimization and closed-loop simulations with various engagement conditions. In future research, the proposed method would be extended to a 3-dimensionl engagement with a nonlinear 6 degree-of-freedom missile model corrupted by various uncertainties. In addition,an onboard implementable solver on the flight computer would be developed to apply the proposed method to the real missile system.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.