VD真空精炼多喷嘴底吹气液两相流的数值模拟
杨 宇,李明明,余 珊,邵 磊,邹宗树
(1.东北大学 多金属共生矿生态化冶金教育部重点实验室,沈阳 110819;2.东北大学 冶金学院,沈阳 110819;3.辽宁科技学院 冶金工程学院,辽宁 本溪 117000)
真空脱气装置(vacuum degasser,VD)是目前应用十分广泛的二次精炼设备,具有钢水脱氢和氮处理、合金成分微调、夹杂物去除、钢水成分及温度均匀化等诸多精炼功能.VD炉精炼过程的顺利进行与底吹氩气搅拌提供的良好流体动力学条件密不可分.因此,研究钢包底吹氩气过程的钢水流动情况并优化底吹氩工艺是提高钢液质量、提升VD真空精炼效率的基础.目前,国内外对底吹氩气钢包流场与混匀效果及其受底吹氩工艺参数(如底吹喷嘴数量和位置、吹氩流量和模式等)的影响规律进行了广泛研究[1-5],但主要针对的是常规钢水冶炼条件下钢包单喷嘴或双喷嘴底吹氩工艺的优化.然而,随着氢冶金在钢铁工业的大力发展,可以预见完全以H2或富H2作为还原剂所生产钢水的[H]含量将显著高于传统转炉钢水.在高氢钢水冶炼的过程中,进一步优化底吹氩工艺、提高精炼效率以满足钢水温降和生产节奏的要求,是VD精炼工艺面临的重要任务.尽管增加底吹氩气流量可在一定程度上提高精炼效率,但受卷渣等因素的影响,通过增加现行单喷嘴或双喷嘴钢包底吹氩气的流量来增强的搅拌效率已很有限[6-7].因此,本文中通过建立VD真空精炼过程氩气、钢液两相流动的数学模型,探究VD精炼炉在多喷嘴底吹条件下钢液的流动与混合特性,并在此基础上考察底吹氩气模式和流量对熔池流体力学行为的影响.
1 数学模型
基本假设:①忽略熔渣层,氩气和钢液视为不可压缩黏性流体;②不考虑化学反应及其对气、液相的影响;③忽略钢包液面波动,认为钢液表面水平;④不考虑气泡的破裂与聚并等气泡间的相互作用;⑤底部和侧壁为无滑移壁面,采用标准壁函数模拟近壁区流动.
采用Eulerian多相流模型模拟氩气、钢液两相流动,气液两相的质量守恒方程和动量守恒方程如式(1)(2)所示.气液两相间的作用力主要考虑曳力和升力.

式中:αq为q相的相分率,%;ρq为q相的密度,kg/m3;uq为q相的速度,m/s;p为压力,pa;g为重力加速度,m/s2.
为了准确地描述钢包内气液两相的湍流流动,同时考虑阻力、尾迹脱落和气泡摆动等气泡运动引起的液体湍流脉动现象,以及气液相间湍流的相互作用,对标准k-ε模型进行修正.修正后的湍流模型可表述为

式中:Sk,Sε分别为两相作用引起的湍流源项[8-9].

式中:σk=1.0,σε=1.3,Cε1=4.0,Cε2=0.6,Ck1=6.0,Ck2= 0.75,C1= 1.43,C2= 1.92,CD= 1.0.其中,Gk是由平均速度梯度引起的湍动能k的产生项,即式(5)(6)等式右边第一项分别表示由于阻力、尾迹脱落和气泡摆动等气泡运动引起的液体湍动能k和耗散能ε的产生项;等式右边第二项是气泡上升运动过程中液相对气泡产生的剪切作用,其与摩擦因数和空隙率成正比.
当钢液达到稳定流动状态时,根据示踪剂的扩散情况来评估混匀过程,将获得95%均匀度所需的时间定义为混匀时间.采用组分输运模型预测示踪剂在钢液中的混合过程,计算中考虑了含气率对组分输运的影响,如式(7)所示.

式中:Sct为湍流施密特数,取值1.0;C为示踪剂的无量纲浓度.
以某钢厂105 t VD真空精炼钢包为原型建立三维数值模型.图1为钢包几何结构示意图及其尺寸.钢包吹氩入口设置为速度入口边界条件,根据实际情况下吹氩流量计算氩气流速,两相流体性质及其他操作参数见表1.钢液表面采用脱气边界条件,即假定为一个平坦的自由表面,搅拌气体完全排出,剩余液体完成循环流动.采用耦合算法计算两相流场,根据流场结果计算示踪剂在钢液中的传输行为.计算收敛标准为离散方程残差小于10-4.

图1 某钢厂105 t VD钢包几何尺寸和结构参数(m)Fig.1 Geometrical dimensions and structure of 105 t VD in a steel plant

表1 流体特性和操作参数Table 1 Fluid characteristics and operating parameters
2 结果与讨论
2.1 数值模型验证
为了验证数学模型的有效性,将本文中的数学模型应用于 Sheng等[8,10]建立的物理模型,并对比数值计算结果与实验结果.图2(a)给出了考虑和不考虑湍流修正(标准k-ε模型)时预测的沿底喷嘴中心轴线方向的液相速度分布与实验测量值的对比,图2(b)为此两种湍流模型预测的液面处液相速度的径向分布与测量值的对比.从图中可以看出,与标准k-ε模型相比,使用修正k-ε模型的计算结果与实验值吻合较好.这表明在钢包内气液两相流动过程中,阻力、尾迹脱落、气泡摆动等气泡运动引起的液体湍流脉动及气液相间湍流的相互作用对两相流动的影响较大,在两相湍流模拟时不可忽略.

图2 液相速度分布的预测值与实验测量值的比较Fig.2 Comparison of the predicted liquid velocity and the measured ones
为验证数值结果的网格无关性,对比了三种网格数量下沿底喷嘴中心轴线方向的液相速度分布,如图3所示.由图可知,当网格数量为45万和55万时,计算结果相差较小.因此,为减小计算成本并保证良好的精度,所有的模拟均采用45万网格数.

图3 不同网格数量下沿底喷嘴中心轴线方向的液相速度分布Fig.3 Liquid velocity distribution along the tuyeres axis for different numbers of grids
2.2 VD精炼多喷嘴底吹两相流场和混合特性
Lou等[11]研究了不同喷嘴数量对气搅拌钢包混合现象的影响,他们发现与单喷嘴中心吹气和偏心吹气相比,双喷嘴吹气的混合时间短.大量研究[12-15]表明,双喷嘴底吹熔池较单喷嘴底吹更能有效改善钢包内溶液的流动和熔池的混合现象,也更有利于提高熔池的混合效率.因此,本文对VD精炼炉多喷嘴底吹熔池的混合现象进行了研究分析.
图4为VD精炼炉不同喷嘴数量的底吹布置方案.基于原型钢包双喷嘴布置方式[图4(a)],设置了多喷嘴布置方式,如图4(b)~(d)所示.其中,双喷嘴径向位置分别为0.57R和0.41R(R为炉底半径),分离角为71.4°,标准状态下吹氩流量为260 L/min(以下均为标准状态).

图4 VD炉多喷嘴布置方式Fig.4 Layout of bottom tuyeres in VD furnace
从表2中可以看出:当采用VD炉原双喷嘴布置时,混匀时间较长,增加喷嘴数量可使混匀时间显著缩短;当采用图4(b)所示的三喷嘴布置时,混匀时间最短,为129 s.与双喷嘴和四喷嘴底吹相比,三喷嘴底吹布置方式使熔池混匀效率分别提高了31.4%和4.7%.

表2 不同喷嘴数量下熔池混匀时间Table 2 Mixing time of molten bath in VD furnace for different numbers of tuyeres
为了进一步阐明引起上述混匀效果的原因,图5和图6分别给出了不同喷嘴数量布置方式下在熔池深度为2.0 m处水平截面上的速度云图和过0.57R喷嘴竖直截面上的速度云图.由图5(a)和6(a)可知,当采用双喷嘴布置时,钢液流动速度较小,在靠近壁面处存在两个较大的弱流动区,且在熔池中心循环流动较弱,钢液整体混合不均匀,混匀效率较低.当喷嘴数量增加到3个时,近壁区钢液流动加强,弱流动区减小,钢液的整体混合均匀且强烈,如图5(b)和图6(b)所示.但需要指出的是,在三喷嘴底吹的条件下,当改变所增加喷嘴的径向位置和夹角时,气泡羽流区钢液的动能明显下降,熔池内弱流动区增大,钢液循环流速减弱且不均匀,混合效果并未得到改善,说明喷嘴布置方式对熔池的流动和混合有较大影响[见图5(c)和图6(c)].当底喷嘴数量进一步增加到 4个时,气泡羽流区钢液具有较大的动能,但由于羽流之间的强干扰作用,气体传输至钢液的搅拌能下降,在靠近壁面和羽流之间的钢液流动变差,如图5(d)和图6(d)所示.从图6中还可以发现,气泡羽流区的液相速度在接近上表面时降低.这主要是因为在出口边界采用的是脱气边界条件,钢液表面被假定为一个平坦的自由表面,搅拌气体完全排出,剩余液体完成熔池循环流动.因此,接近上表面处的液相速度极低,出口界面处的钢液动量为0.

图5 不同喷嘴数量布置方式下熔池深度为2.0 m处水平截面上的速度云图Fig.5 Velocity contours on horizontal section at the bath depth of 2.0 m for different numbers of tuyeres
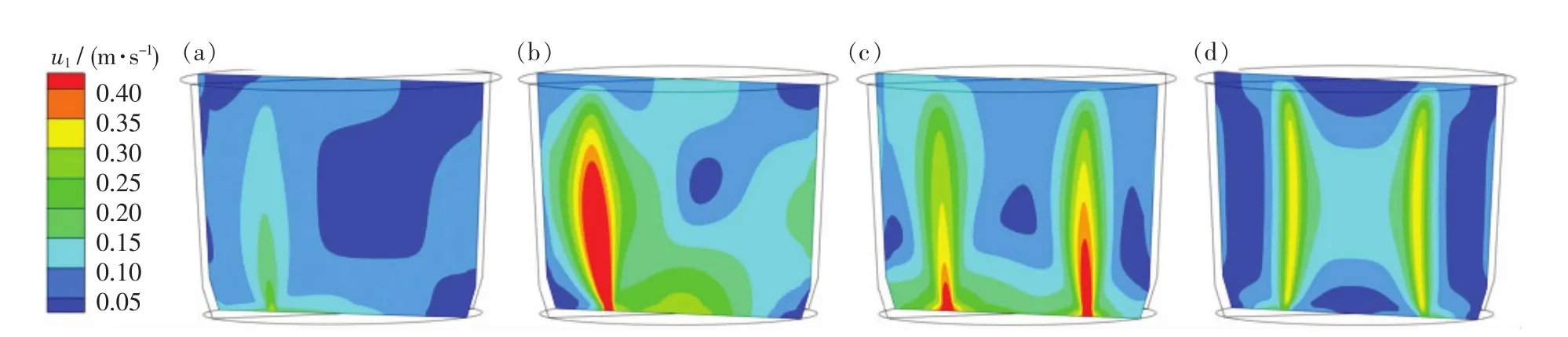
图6 不同喷嘴数量布置方式下过0.57R喷嘴竖直截面上的速度云图Fig.6 Velocity contours on vertical section at 0.57R for different numbers of tuyeres
2.3 底吹供气模式的影响
研究表明[16],不同供气模式(均匀供气和非均匀供气)会影响底吹钢包系统对熔池的搅拌效果.根据前文对喷嘴数量的优化结果,采用图4(b)所示的三喷嘴底吹布置方式分析供气模式的影响.在保持总底吹供气流量相同的条件下,研究不同的非均匀供气方案对熔池混匀的影响.分配原则如下:靠近熔池底中心的喷嘴采用弱气流量对钢包底部弱流区进行搅拌,而远离熔池底中心的喷嘴则采用强气流量对整个钢包进行搅拌,从而形成大的循环流量,在一定程度上降低气体搅拌的能量耗散.氩气流量为260 L/min,流量分配按图7所示的入口顺序设置.假设供气模式为1∶1∶1(均匀供气)与 2 ∶1 ∶1,3 ∶2 ∶1,1∶2∶3,1∶2∶2,2∶3∶3(非均匀供气).

图7 底吹流量分配模式Fig.7 Gas distribution modes for bottom tuyeres
从表3可以看出:随着入口1流量分配比的增大,混匀时间逐渐减少;当3个喷嘴的流量分配比为3∶2∶1时混匀时间最短,为124 s;当入口2和入口3流量分配比增大时,混匀时间显著增加.综上可知,提高近壁区喷嘴的流量分配比可达到改善熔池动力学条件的作用.
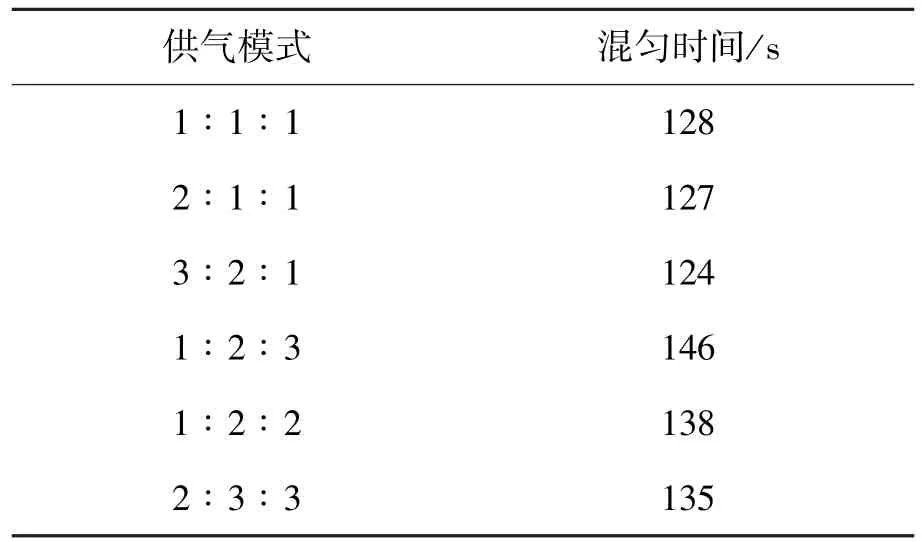
表3 不同供气模式对混匀时间的影响Table 3 Effect of gas injection modes on bath mixing time
图8和图9分别给出了不同供气模式下过入口1、入口2竖直截面上的矢量图和熔池深度为2.0 m处水平截面上的速度云图.由图8(a)~(c)和图9(a)~(c)可知,随着入口1流量分配比的增大,钢液流动速度增加,靠近壁面处的弱流动区逐渐减小,熔池内循环流动逐渐均匀而稳定.当入口2和3流量分配比增大时,钢液流动速度较小,循环流动减弱,如图8(d)~(f)和图9(d)~(f)所示.因此,当采用3∶2∶1供气模式时,混匀时间最短,说明此模式下熔池的混合现象最好,可获得VD真空精炼最优熔池动力学条件.

图8 不同供气模式下过入口1和入口2竖直截面上的矢量图Fig.8 Velocity vectors on vertical section through tuyeres 1 and 2 for different gas injection modes

图9 不同供气模式下熔池深度为2.0 m处水平截面上的速度云图Fig.9 Velocity contours on horizontal section at the bath depth of 2.0 m for different gas injection modes
2.4 底吹氩气流量的影响
在3∶2∶1的非均匀三喷嘴供气模式下,表4给出了气体流量在50~500 L/min内熔池的混匀时间.结果表明,随着底吹氩气流量的增大,熔池的混匀时间先减少而后增加.当采用较小的底吹氩气流量(50 L/min)时,熔池混匀时间较长,为155 s;当吹气流量增大到100 L/min时,混匀时间减少到118 s;而当底吹氩气流量进一步增大时,混匀时间开始逐渐延长.这是由于底吹氩是钢液流动的动力来源,当小气体流量底吹时,气体的搅拌能较小;当气体流量增大时,气泡上浮的动能增大,促进了钢液流动,熔池混匀时间变短;当底吹氩气流量超过某一临界值时,在各羽流区会形成“通道效应”[17],气流将快速上升到熔池表面,导致其在熔池中的停留时间变短,这极其不利于气液间的动量传递.因此,在采用3∶2∶1的非均匀三喷嘴供气模式时,最佳吹氩流量为100 L/min.

表4 气体流量对混匀时间的影响Table 4 Effect of gas flow rate on mixing time
3 结 论
(1)通过考虑气液两相流动过程中阻力、尾迹脱落、气泡摆动等气泡运动引起的液相湍流脉动及两相间湍流的相互作用,建立了可准确描述VD真空精炼过程气液两相流动的数学模型.
(2)多喷嘴底吹可有效改善钢包内熔池的混合现象.当采用三喷嘴底吹时,熔池的混合效率高于双喷嘴和四喷嘴底吹.
(3)当采用三喷嘴底吹时,提高近壁区喷嘴的流量分配比可强化熔池搅拌,且3∶2∶1的非均匀供气模式可达到最佳熔池混合效果.
(4)在3∶2∶1的非均匀三喷嘴供气模式下,随气体流量的增加,混匀时间存在一个临界最小值;当底吹氩气流量为100 L/min时,混匀时间最短,为118 s.

