基于MIG 的电弧增材制造熔池行为的数值模拟

张天雷, 徐 刚, 沈艳涛, 何林基, 马春伟

(1 上海工程技术大学 材料工程学院, 上海201620； 2 北京海基科技发展有限责任公司, 北京100192)

0 引 言

增材制造(Additive Manufacturing, AM),也称为3D 打印,是通过三维建模,切片处理,逐层制造的技术［1］。 金属增材制造主要包括四类：粉末床熔融(PBF, Powder Bed Fusion),直接能量沉积(DED,Direct Energy Deposition), 粘结剂喷射(Binder Jetting)和薄材叠层(Sheet Lamination)。 直接能量沉积法中的金属材料可以是粉末或者丝材,热源可选择激光、电子束和电弧［2］。 基于MIG(Metal Inert-Gas Welding) 的电弧增材制造(Wire and Are Additive Manufacturing, WAAM )是以焊接电弧为热源,在惰性气体的保护下,焊丝通过送丝机构传送到焊枪,并在电弧的作用下融化,以点-线-面-体的形式制造工件,具有沉积效率高、打印尺寸大、零件致密度高、材料及设备便宜等优点［3］。

由于增材制造环境复杂,其熔池温度较高,很难用实验方法观测到熔池行为。 而数值方法不仅可以模拟熔池的相变过程,还可以进一步计算分析表面张力、电磁力、浮力、熔池重力、电弧压力和熔滴过渡等对熔池形貌和内部流动的影响［4］。 由于使用焊接工艺,电弧增材制造过程中传热特征和焊接熔池类似。 国内外学者建立了多种CFD 模型模拟焊接过程熔池行为,Rao 等人建立了三维数值模型研究周期性熔滴过渡对焊接熔池传热和传质的影响。 尽管电弧增材使用焊接工艺,但是相比于焊接电弧增材的熔池,是在前一层熔覆层的曲面上生成,而不是在平板上或者预先加工的坡口中形成,没有了基板的支撑,电弧增材制造的熔池更加不稳定,熔滴过渡对熔池的影响更大；zhao 等人建立了三维数值模型,模拟了电弧增材制造过程中的电弧形态和熔滴过渡过程；Hu 等人模拟了基于电子束增材制造的传热和传质的耦合行为；Bai 等人建立了基于等离子弧的电弧增材制造过程多层熔覆过程模拟,分析了层高及弧坑对熔池的影响；Ou 等人建立了单道单层的电弧增材制造模型,分析了熔池速度场、温度场的特性。 此模型的熔池是在平板上形成,没有考虑多层堆积过程中熔池在曲面上形成时的特性。

本研究采用FLUENT 软件,耦合多相流VOF 模型和融化凝固模型,基于自由表面,建立基于MIG的电弧增材制造的三维熔池数值模型,模拟了熔池在曲面上生成、流动及相变情况,分析了多场耦合下熔池表面变形以及温度场和速度场的变化规律,并探讨了熔滴过渡对熔池的影响。

1 电弧增材制造熔池有限元模型的建立

1.1 基本假设

图1 为基于MIG 的电弧增材制造示意图。 由于其物理过程非常复杂,为了简化计算做如下假设：(1)熔池中液态金属为非可压牛顿流体,其流动方式为层流。 (2)将焊接电弧传热的能量,以双椭球热源形式代替。 (3)金属材料的热物理属性除粘度,热导率,比热容外其余皆为常数。 (4)熔滴的温度,直径和频率皆为固定值。

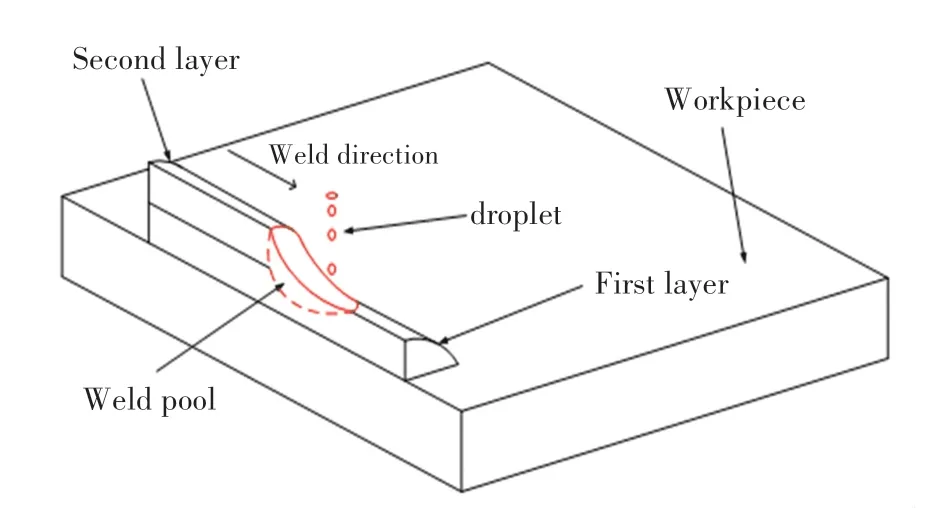
图1 电弧增材制造示意图Fig. 1 The schematic of wire and arc additive manufacturing

1.2 控制方程

通过求解流体力学中的三大守恒方程来计算电弧增材制造过程中的传热传质和流体流动过程。 采用多相流VOF 模型追踪金属和气体的自由表面。

连续性方程(1)：

式中,ρ 为密度,V 为速度矢量,SC为熔滴质量源项。

动量方程(2)：

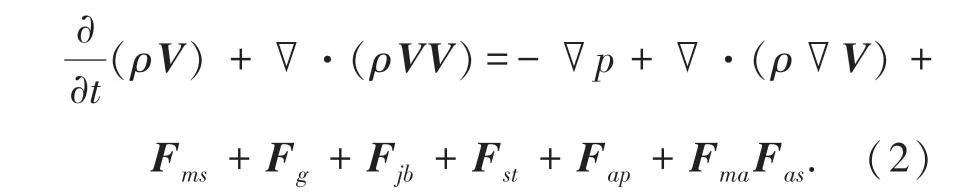
式中,p 为压力,V 为流体粘度,Fms为焓-孔隙度模型的动量源项,Fg为重力源项,Fjb为电磁力源项,Fst为表面张力源项,Fap为电弧压力源项,Fma为马拉格尼力源项,Fas为电弧剪切力源项。

能量方程(3)：

式中,qarc为电弧能量源项,qmetal为熔滴热量源项,qloss为热对流和热辐射散失的能量源项。

式中,F 为多相流中相占网格的体积分数,若网格中占满某一相则该相F = 1；若网格中不含某一相,则该相F=0；若网格中某相F 介于0 到1 之间则表面该网格在相界面上,用此方法来追踪金属和气体的自由界面。

1.3 相变模型

在FLUENT 融化模型中,运用焓-多空度技术处理糊状区为一个多空区域,用来追踪凝固过程中的固液界面,fl为网格中液体的体积分数,其值与温度相关的方程表示如下［5］：

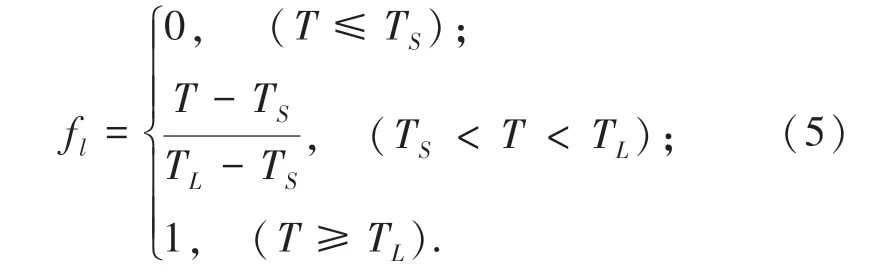
式中,TS为固相线温度,TL为液相线温度。

在焓-多空度模型中加入一个动量源项,用来使糊状区和固体区的速度衰减,其表达式(6)：

式中,Fms为焓-孔隙度模型的动量源项；Amushy为糊状区常数,用来表示糊状区域速度衰减的快慢,其值在104 到107 之间,数值越大速度衰减越快,如果数值过大会出现凝固震荡；ε0为一个不为零的小数其值为0.001,防止分母为0。

1.4 电弧增材制造热力模型

1.4.1 热源模型

由于电弧增材过程中熔池上表面不再是平面,传统的双椭球热源模型已不能完全反应电弧增材制造的热源,因此基于双椭球热源修改为双椭球上表面随熔池自由变化的自适应热源,公式(7)、公式(8)如下［6］：

其中,qar为前半椭球热源分布,qaf为后半椭球热源分布,x0,y0为热源起始点坐标,zS为熔池上表面z 方向坐标值,VT为热源移动速度,t 为热源移动时间,a1,a2,b,c 为双椭球热源参数。

1.4.2 电磁力模型

在前人简化的电磁力基础上,将电磁力作用区域改为随熔池表面变化的自适应模型,方程(9)～方程(12)如下：

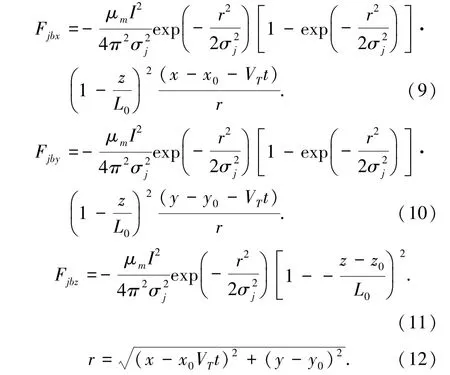
其中,Fjbx为x 方向电磁力源项,Fjby 为y 方向电磁力源项,Fjbz为z 方向电磁力源项,σj为电弧密度分布,r 为xy 平上半径,z0为熔池上表面坐标。

1.4.3 浮力

电弧增材制造过程中,熔池所收到的浮力可用Boussinesq 近似替代,浮力表达式(13)如下：

其中,Fb为浮力源项,ρ 为金属密度,β 为热膨胀系数,g 为重力加速度,T 为温度,Tm 为金属熔点。

1.4.4 电弧压力和剪切力模型

根据双椭球体热源的特征,电弧压力简化为双椭圆分布,方程(13)、(14)如下［7］：

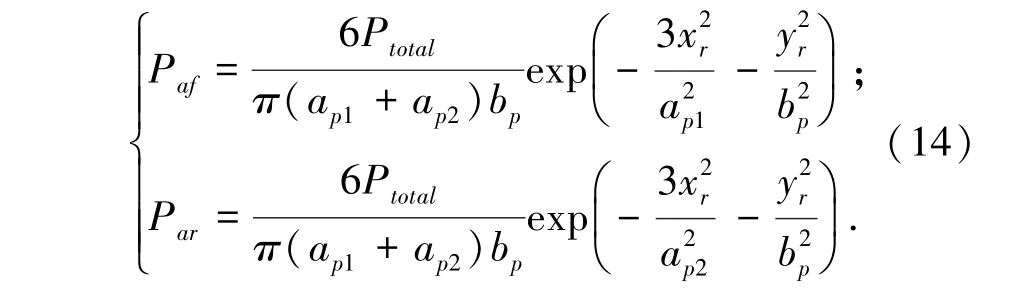
式中,ap1, ap2, bp为形状分布系数,Paf为前半球电弧压力,Par为后半球压力,Ptotal为电弧总压力。

电弧总压力根据公式(15) 计算［8］：

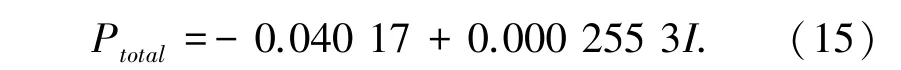
其中,I 为焊接电流。

电弧剪切力简化模型如公式(16)所示［9］：

式中,R0为雷诺数,Ha为焊枪口到熔池表面的距离,Dn为焊丝直径,g2是通用方程；vp0是电弧等离子弧速度。

等离子弧速度由公式(17)求解：

式中：kp为计算系数,本例中为0.5,I 为焊接电流。

1.4.5 熔滴过渡模型

在计算过程中熔滴被假设为高温的液滴,以固定的初速度和频率过渡到熔池中。 熔滴直径为焊丝直径,熔滴温度设定为2400K。 熔滴过渡频率取决于送丝速度和熔滴速度。

熔滴初速度计算公式(18)如下［17］：

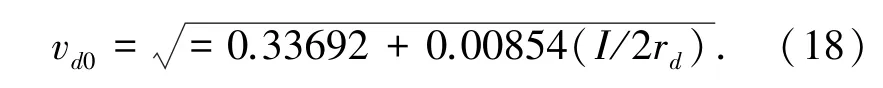
其中,rd为焊丝半径,I 为焊接电流,vd0为熔滴初速度。

1.5 边界条件

在模拟过程中基板及熔池表面考虑对流换热和辐射散热,为了简化计算,建立对称模型,中心对称面为绝热面。 空气域四周为压力出口边界条件,熔池上方为以焊丝直径为圆形的速度入口边界,计算公式(19)如下：

其中,hc为对流换热系数,T0为环境温度,式中σ 为Stenfan-Boltzmann 参数；ε 为表面辐射。

1.6 网格划分及实验数据

模型计算尺寸为25 mm×10 mm×11.5 mm,基板厚度5 mm,第一层熔覆层根据实验数据建立,主要模拟第二层熔池在曲面上形成过程。 采用Gambit软件进行网格划分,基板厚度方向近熔池区域为加密网格,远离熔池区域为稀疏网格,最小网格尺寸为0.25 mm,网格总数为6 800,节点总数为74 235。

实验基板为SU304 不锈钢,焊丝为ER308,假定两者的热物理属性相同,其参数如表1 所示［10］。

表1 材料物理属性Tab. 1 The material physical properties

仿真过程参数根据实验参数确定,电弧增材制造过程工艺参数如表2 所示。

表2 工艺参数Tab. 2 Process parameters

2 结果与分析

2.1 熔池表面形貌

电弧增材制造熔池是由焊丝融化过渡到基板或前一层熔覆层和基板或前一熔覆层融化的金属部分组成,图2 是电弧增材制造过程中0 s-3 s 的熔池表面形貌和温度场演变的过程。 由图2(a)和(b)可以看出,在0 s-1 s 熔池形成初期阶段,熔池在表面张力的作用下,成近半球形的状态；由图2(c)的(d)可以看出,在熔池长大阶段,由于焊丝向焊接方向移动,熔滴过渡向前,熔池被拉长,熔池前方在电弧压力的作用下,导致熔池前方液态金属少,熔池后方液态金属多,形成熔池前方低、后方高近似楔形的形状。 由图2(e)和(f)可以发现,当电弧增材2 s 之后熔池形貌基本稳定,由于熔池在曲面上形成,熔池两侧没有支撑熔池有向两侧流动的倾向。

图2 熔池表面形貌演变过程Fig. 2 Themolten pool surface evolution

2.2 熔池温度场和流场

2.2.1 熔池横界面温度场和流场

图3 为电弧增材过制造程2.000 s-2.010 s 时,熔滴过渡不同时刻的熔池横截面温度场和流场分布。 图3(a)为2.000 s 时熔滴刚形成还未脱落。 由于焊接速度较快,熔池前半主要受电弧热源和熔滴热焓作用,材料没有来得及完全融化,呈现出熔池前方熔深较小,融化后方熔深较大的现象。 在电弧压力作用下,熔池前方电弧作用区呈现斜坡式形态,液态金属在马拉格尼力作用下向后方移动,在熔池内部形成逆时针环流；由图3(b)可以看出,当2.025 s时熔滴完全生成,开始过渡到熔池中,由于焊接电流为电流熔滴以大滴形式过渡,熔滴直径约为1.2 mm,熔滴速度在0.5 m／s 左右；当时间为2.075 s时,如图3(c)熔滴完全落入熔池中,熔池上表面受到熔滴的冲击形成凹陷面；当时间为2.01 s 时,如图3(d)所示,被熔滴冲击的凹陷面被周围液态金属填充,焊接熔池在周期性熔滴过渡的影响下,熔池也呈现出周期性的波动状态。

2.2.2 熔池纵截面温度场和流场

如图4 所示为焊接时间为2.0 s 时,熔池的不同位置横截面温度场和速度场分布。

图3 熔池纵截面温度场和流场Fig. 3 Temperature fields and velocity fields inlongitudinal section

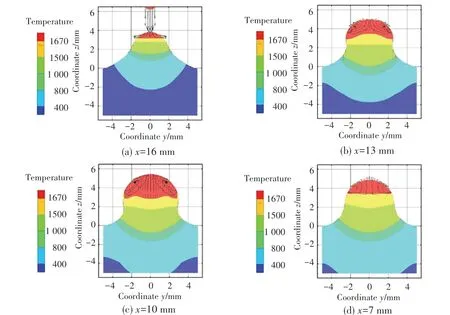
图4 熔池横截面温度场和流场Fig. 4 Temperature fields and velocity fields in cross section

图4(a)为x = 16 mm熔滴正下方熔池横截面,熔池在表面张力作用下,呈现出凸面的形态,由于金属熔化需要一定时间,熔池在熔滴正下方熔深很小；熔池中部如图4(b) x = 13 和图4(c) x = 10 所示,熔池深度加深,熔池表面受表面张力的作用形成半球面状态,熔池表面温度分布不均,在马拉格尼力作用下,由中心流向两侧。 由于熔池两侧没有固态金属的支撑,流向熔池两侧的金属在重力作用下,有向下流淌的趋势,在表面张力的作用下未脱落形成圆弧的形态。 由于熔池上表面液态金属流向熔池两侧,熔池中心液态金属向上流动,熔池底部金属向熔池中心填充形成回流。 在熔池后方如图4(d) x = 6所示,液态金属减少,熔池开始凝固,温度场向底部传导,温度场分布较熔池前方均匀。

2.3 实验验证

为了验证上述模型的可行性和准确性,对模拟结果和试验结果做了对比验证,图5 为熔池横截面实验与模拟形貌对比,可见熔池的界面的计算结果和试验结果吻合良好,说明此电弧增材制造熔池计算模型合理。

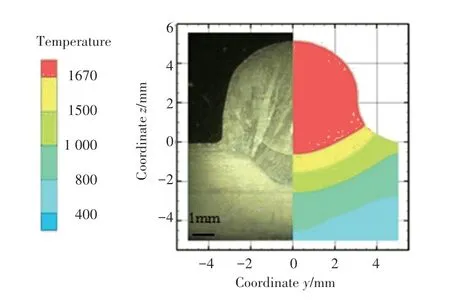
图5 熔池横截面实验结果与模拟结果对比Fig. 5 Comparison of simulated molten pool shape with actual molten pool morphology

3 结束语

(1)基于fluent 软件考虑熔滴过渡和电弧热力耦合,通过VOF 方法追踪自由界面建立的自适应热源,电弧压力和电磁力,建立了适合基于MIG 的电弧增材制造熔池数值模型,通过数值模拟结果和试验结果对比,验证了模型的可靠性,为后续研究提供了基础。

(2)电弧增材制造熔池开始阶段在表面张力作用下为圆形,随着熔池向前移动,在电弧压力作用下呈现熔池前方低,后方高的锲型状态。

(3)电弧增材制造熔池在凸曲面平面上形成时,熔池两侧有没支撑的情况下,熔池两侧有向下流淌的趋势,在表面张力作用下保持平衡。