基于随机矩阵建模的Student’s t逆Wishart滤波器

陈 辉 ,王 莉 ,韩崇昭

(1.兰州理工大学电气工程与信息工程学院,甘肃兰州 730050;2.西安交通大学自动化科学与工程学院,陕西西安 710049)

1 引言

随着电子技术和信息处理技术的高速发展,高分辨率传感器的广泛应用显著提升了目标跟踪与识别技术的发展.利用高分辨率传感器获取的目标量测集不仅能对目标的运动学状态进行估计,同时也可对目标的形状轮廓等特征信息进行有效提取,此类目标被称为扩展目标(extended target,ET),其对应的跟踪问题称之为扩展目标跟踪(ET tracking,ETT)[1–4].与传统的点目标相比,扩展目标通常对应一定空间范围中的多源量测信息,如图1所示.

扩展目标的量测信息产生的方式和点目标有很大不同,首先需要确定量测源模型,然后从量测源模型中合并噪声随机生成目标量测.量测源模型代表了环绕目标质心一定空间范围的量测分布状况,如图1中所示,常见的量测源模型有矩形、椭圆形、星凸形等.图2为扩展目标量测源生成的过程.

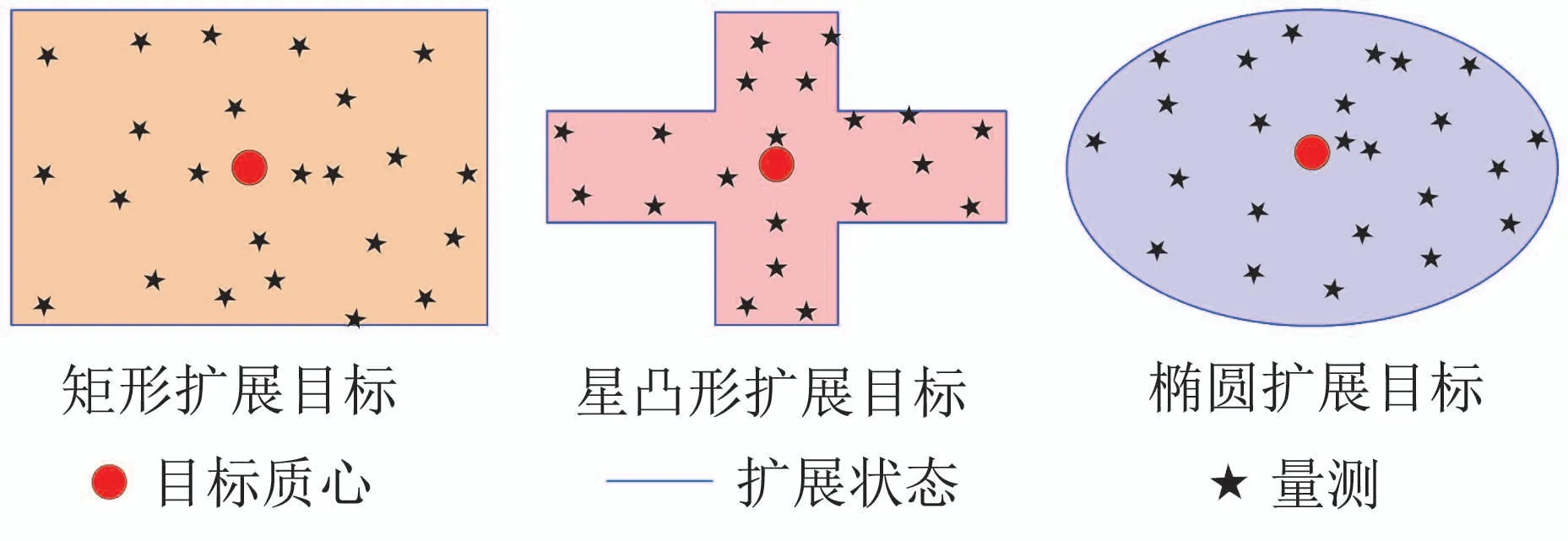
图1 不同量测源的扩展目标示意图Fig.1 Schematic diagram of extended targets for different measurement sources

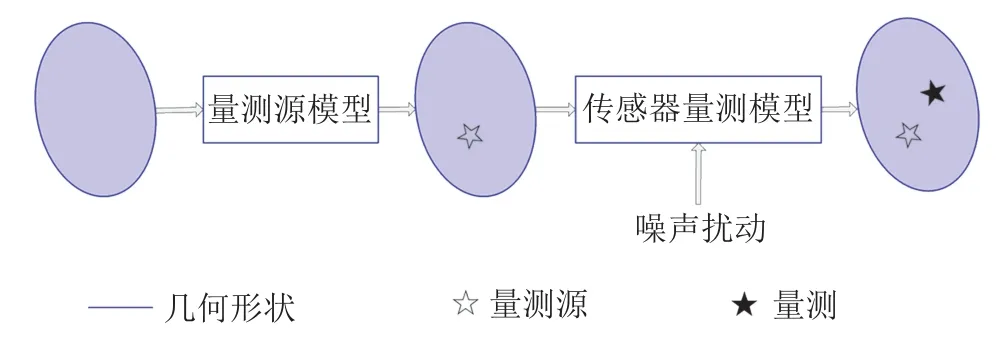
图2 扩展目标生成量测示意图Fig.2 Schematic diagram of extended target generation measurement

Gilholm等假设扩展目标量测个数服从泊松(Possion)分布[5],但该量测源模型在空间上的分布并不明晰,这种量测产生的方式在实际应用中也很难实现.更进一步地,Koch提出将扩展目标的量测源模型近似为椭圆[6],且用随机矩阵模型(random martix model,RMM)来描述带有大小和方向的椭圆轮廓特征.RMM被建模为逆Wishart分布,而目标的运动学状态被建模为Gauss分布,运用贝叶斯递推可得扩展目标高斯逆Wishart滤波器,从而实现扩展目标运动学状态和形状扩展状态的联合估计[7–8].Feldmann等对RMM方法进行了改进,引入量测噪声对扩展目标形状估计的影响[9–10],从而形成了更为精确的椭圆扩展目标形状建模.YANG等人提出用乘性噪声模型(multiplicative noise model,MNM)对目标的空间分布建模[11],MNM的核心思想是将目标空间分布模型的一个子类表述为一个带有乘性噪声的显示量测方程,通过MNM将目标量测源模型与目标形状参数联系起来,并引入二阶扩展卡尔曼滤波器(second-oreder extended Kalman filter,SOEKF)[12]来递推目标运动学状态和形状参数协方差矩阵的闭环解析表达式,从而实现椭圆扩展目标的运动学状态和扩展状态的联合估计.Baum提出经典的随机超曲面模型[13](random hypersurface model,RHM),其主要思想是基于傅里叶级数展开实现不规则轮廓曲线的拟合,并引入尺度因子缩放目标形状边界从而对目标量测源分布进行合理建模.扩展目标的不规则形状还可以利用高斯过程回归[14–15](Gaussian process regression,GPR)进行建模,该方法基于高斯过程的学习特性描述目标形状的径向函数,可对复杂星凸形目标形状的局部轮廓进行更加灵活的建模.此外,可利用水平集随机超曲面模型(levelset RHM)[16]对任意非星凸型目标形状进行准确估计,该模型利用隐函数的level-set对形状的内部进行建模.然而,以上各种不规则形状扩展目标建模方法受制于扩展目标量测源的质量和量测数目,而椭圆形建模目前仍旧是针对雷达的稀疏量测集较为合理的建模方式,它保证了扩展目标基本轮廓特征和方向信息的有效提取,对目标的快速识别奠定了坚实的基础.

在现实的工况环境中,由于信号传输的随机延迟和传感器自身的不可靠性等,很容易导致离均值较远处的不确定性变大,这就使得系统的量测噪声的分布特性呈现出明显的“厚尾特性”[17–19].而且在目标的跟踪过程中,目标可能会发生机动,也会使得过程噪声分布呈现出同样的“厚尾特性”,继续沿用传统高斯滤波器会因为过程噪声和量测噪声的建模不匹配严重影响滤波器的估计性能[20–22].文献[23–25]提出在高斯假设下通过重加权方法对厚尾过程噪声和量测噪声进行同时处理,但高斯假设的前提仍然使得该方法处理厚尾噪声的能力大大受限.Roth等在文献[26]中提出了一种基于学生t(Student’s t)分布的线性滤波方法,该方法通过将噪声建模为对野值包容度更好的Student’s t分布,运用Student’s t分布来逼近目标的后验概率密度函数,使得滤波器对异常噪声呈现出更好的鲁棒性.进一步的,Huang等提出了非线性鲁棒Student’s t滤波器[27],并在此基础上对该滤波器进一步优化,利用三阶球面径向容积采样规则,提出了厚尾噪声条件下鲁棒Student’s t 容积非线性滤波算法[28],使得该滤波器在高维非线性厚尾噪声系统中仍具有较好的适用性.综上所述,相较于传统的高斯滤波器,Student’s t滤波器在处理厚尾噪声方面呈现出明显的优越性.那么,对于更为复杂的扩展目标跟踪问题,受厚尾过程噪声和多源量测厚尾噪声的联合影响,势必会对扩展目标的运动学状态和形状估计产生极为不利的影响,因而对于该问题的研究刻不容缓.

有鉴于此,本文的主要工作是:在异常噪声条件下,利用随机矩阵方法,着重研究椭圆扩展目标运动状态和形状联合估计的方法.本文利用Student’s t分布对受厚尾噪声影响的目标运动学状态进行建模,利用逆Wishart分布对目标的椭圆形状进行数学建模,形成Student’s t逆Wishart联合分布,并通过详细推导过程提出厚尾噪声条件下基于椭圆形状假设的Student’s t逆Wishart(Student’s t Inverse Wishart,StIW)滤波器.最后,通过构建相应的仿真场景验证了所提算法的有效性.

2 系统建模

与点目标不同的是,扩展目标动态模型刻画了目标两个方面即运动学状态演变和扩展状态演变的过程,假设k时刻扩展目标的状态集合为

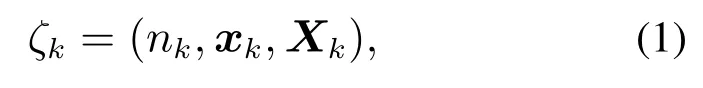
其中:nk是量测的个数;xk是目标运动状态变量,包含目标的位置(x,y)和速度,可表示为xk=[x y]T;Xk是目标的形状(扩展)状态.

1) 目标运动模型.

通常情况下,扩展目标运动状态模型可描述为

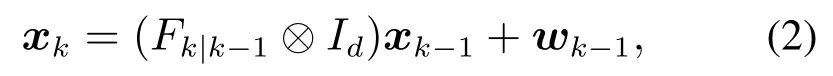
式中:wk表示该跟踪系统的过程噪声;Id表示d×d维的单位矩阵;⊗表示克罗内克积(Kronecker product);Fk|k−1表示状态转移矩阵.

2) 形状演化模型.

由于扩展目标的形状也会随时间进行演化,形状演化模型可刻画目标大小及方向的变化.假设随机正定矩阵Xk服从逆Wishart分布,逆Wishart分布是在实值正定矩阵上定义的概率分布,该分布是逆伽马分布的多元扩展,在整数自由度情况下可以简化为逆卡方分布的多元扩展.由于椭圆形轮廓的分布特征能很好地利用逆Wishart分布生成的随机协方差矩阵所表征,所以利用逆Wishart分布提取椭圆形轮廓具有建模形式上的合理性和便利性.在贝叶斯统计中,逆Wishart分布在贝叶斯滤波中的的共轭先验性已得到严格证明,可有效利用逆Wishart分布共轭先验性质对随机矩阵进行建模,这可有效实现扩展目标运动状态和形状信息的联合递推估计.逆Wishart分布概率密度函数为

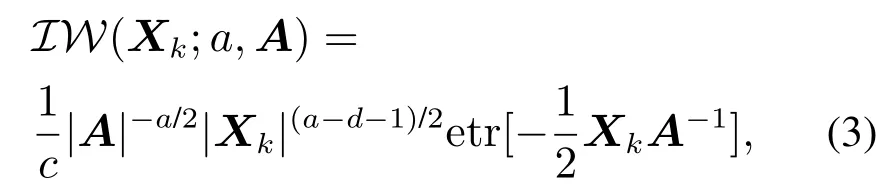
其中:A为d×d维常正定矩阵;标量自由度参数a≥d;etr[·]为exp[tr(·)]的简写;c为归一化因子.

对形状随机矩阵Xk的动态模型做如下两个假设.

假设1 Xk的概率密度转移函数服从逆Wishart分布,即

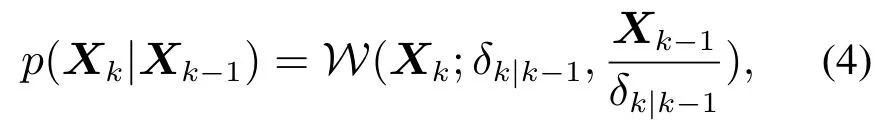
该式表明了随机矩阵从k −1时刻到k时刻的变化规律,标量δk|k−1为自由度参数,描述演化过程中形状大小的变化.

假设2k −1时刻的目标扩展后验概率密度函数服从逆Wishart分布,即

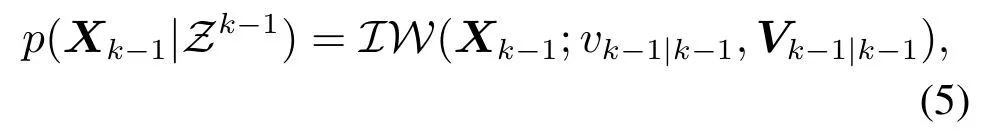
式中:Zk−1为前k −1个时刻得到的全部量测值;vk−1|k−1为逆Wishart分布的自由度参数;Vk−1|k−1为其参数矩阵.

3) 量测模型.

定义k时刻扩展目标产生的nk个量测的集合为,而为前k个时刻得到的所有量测的集合.假设量测的个数nk服从均值为np的Possion分布[9,29],量测的分布模型为

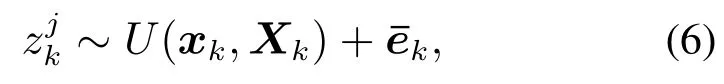
即量测在椭圆表面均匀分布,为量测噪声.

上述量测模型在Bayes框架下难以直接应用,可将其近似如下[9–10]:

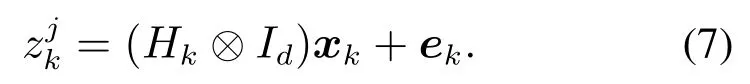
该式合理刻画了扩展目标空间背景中的量测生成,其中的噪声ek联合考虑了由目标的空间扩展(椭圆形状范围)和量测噪声共同引起的量测不确定性,其中的加性随机性看成是系统的背景噪声,且p(ek)相关于Xk和ek的函数,具有直观且明确的物理意义.

4) 异常噪声模型.

复杂的跟踪环境下传感器容易出现异常量测值,导致离均值较远处的量测噪声的不确定性增大,包含“位于某个整体分布模式之外”的异常量测数据,呈现比较明显的“厚尾特性”,因此,过程和量测模型往往同时伴随着不可避免的厚尾噪声,会严重降低以传统高斯分布为前提假设的多目标跟踪性能.例如,扩展目标在运动过程中会出现很大的机动,这种未知的动态模型会带来过程噪声的离群值,呈现出明显的厚尾特性.而如电磁干扰、传感器故障、环境中意外(电磁)干扰、传感器自身不可靠性等,极易导致量测噪声的离群值,扩展目标的多个量测也会呈现出明显的厚尾特性.如图3所示,Student’s t分布显然对异常值的包容性更好,应用该分布对厚尾噪声建模更加合理,其概率密度函数可表示为

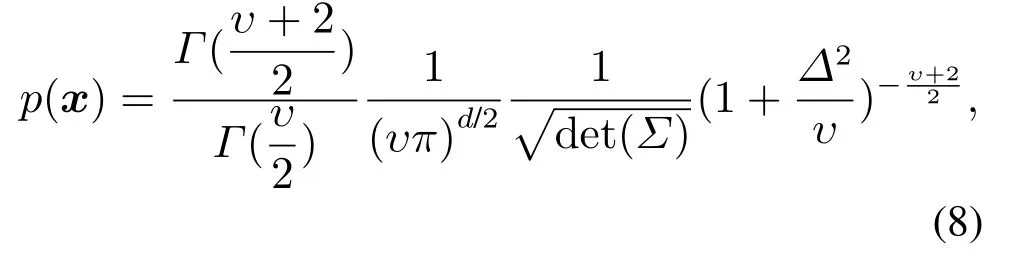
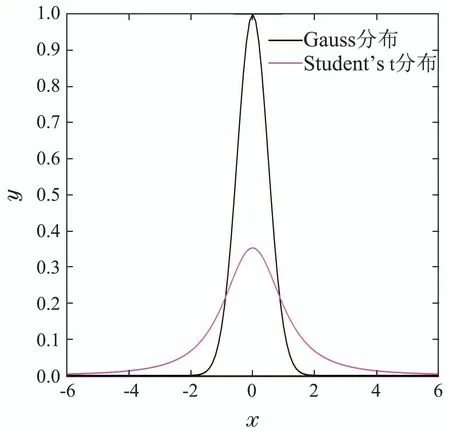
图3 Student’s t分布与Gauss分布对比图Fig.3 Comparison of Student’s t distribution and Gauss distribution diagram

将式(8)简记为St(x;µ,Σ,υ),表示随机变量x服从均值为µ,尺度矩阵为Σ,自由度参数为υ的Student’s t分布,且其尺度矩阵与协方差矩阵所满足的数学关系为.由此可将异常的过程噪声和量测噪声建模如下:

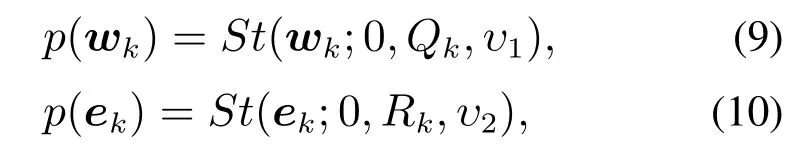
其中:Qk和υ1表示异常过程噪声wk的尺度矩阵和自由度参数,该尺度矩阵表示为Qk=Dk|k−1⊗Xk.Dk|k−1是s×s维的矩阵,为动力学模型参数(即质心运动过程噪声参数).Qk表明目标运动状态的演变与目标的形态变化有关.Rk和υ2表示异常量测噪声ek的尺度矩阵和自由度参数.

如前所述,量测的散布程度受目标轮廓特征的影响,并用收缩因子ε来表征该影响程度,则对量测噪声进一步建模可得

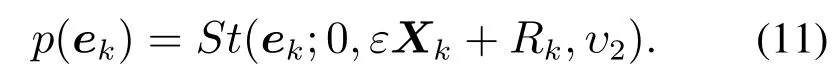
在上述建模的基础上,研究厚尾噪声条件下扩展目标跟踪问题.

注1本文中的自由度参数υ1,υ2,υ3的初始取值为3.根据Student’s t分布的尺度矩阵与协方差矩阵的关系式,需要满足υ >2.但由于Student’s t分布的期望和协方差对厚尾特性比较敏感,在υ →∞时,Student’s t分布会失去其厚尾特性而接近于高斯分布,为了避免这种情况发生,υ的取值不宜过大,为了更契合工程实际,υ1,υ2,υ3的初始自由度一般取值为3.

3 Student’s t逆Wishart滤波器

根据给出的扩展目标和厚尾噪声的基本建模,以下将重点研究厚尾噪声条件下基于RMM的Student’s t逆Wishart(StIW)滤波算法.

从Bayes滤波的角度,递推将获得k时刻的联合后验概率密度函数p(xk,Xk|Zk).该函数可表示为

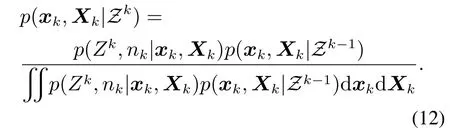
3.1 预测过程

一步预测需要对预测密度p(xk,Xk|Zk−1)进行求解,预测密度计算式可表示为

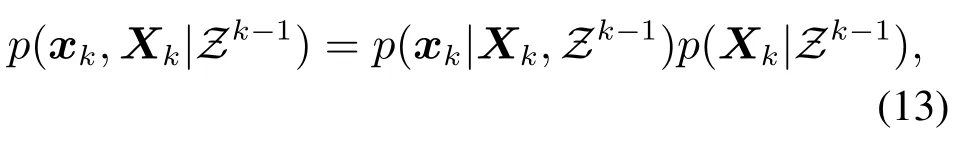
由上式可看出,一步预测密度可分为目标运动学部分和形状扩展部分.

a) 目标运动学部分.

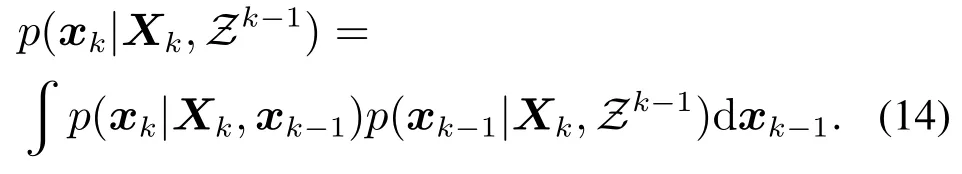
利用Student’s t分布逼近系统的后验概率分布,并做如下假设.

假设3k −1时刻目标运动学状态变量服从Student’s t分布,即

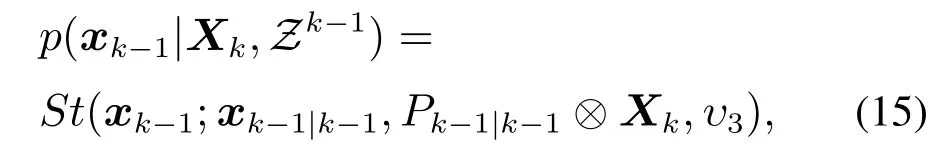
则一步预测计算式为

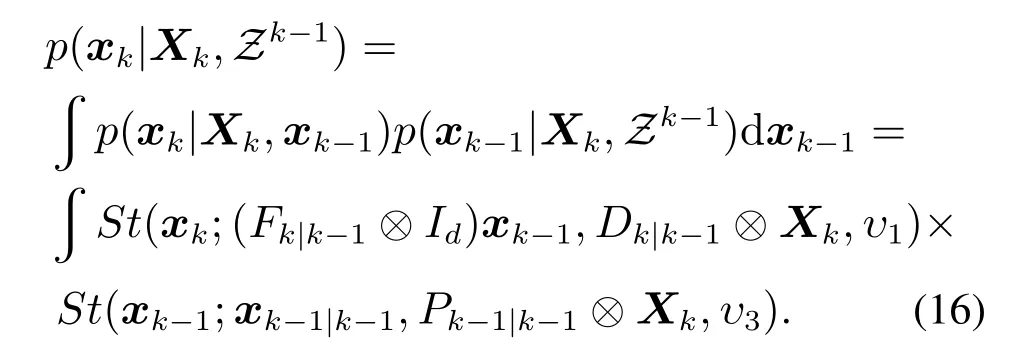
根据Chapman-Kolmogorov方程和Student’s t随机变量的仿射变换[30]得到引理1:

引理1若P和Q均为正定矩阵,则有

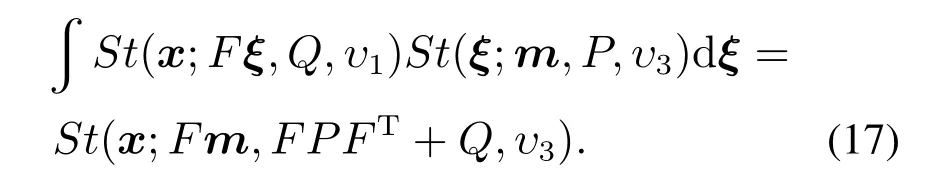
由引理1可将式(16)求解得到

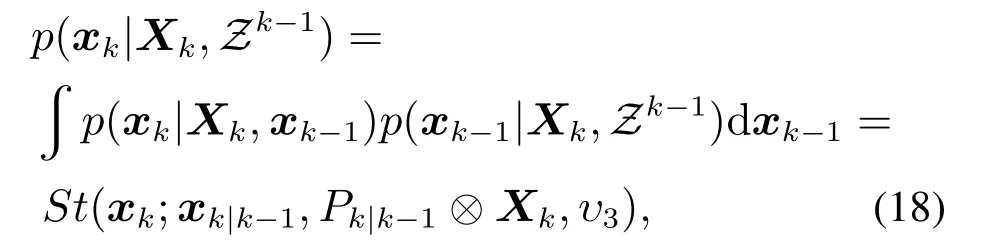
其中:

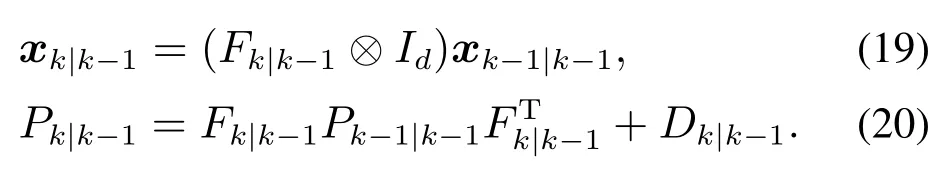
b) 目标扩展部分.

目标的扩展状态被建模为椭圆,可用一个正定矩阵Xk来描述,即

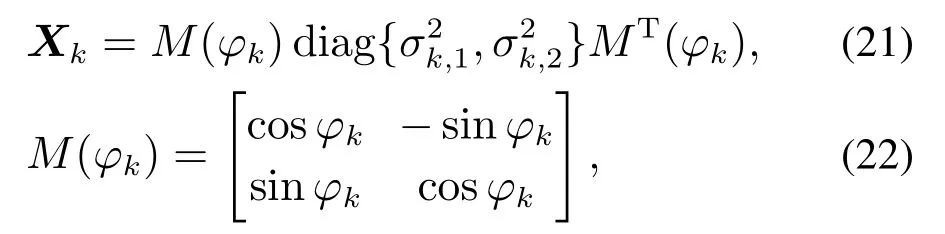
其中:M(φk)为旋转矩阵,椭圆的中心点即目标的质心由运动学状态xk的位置分量确定,长短轴由Xk的特征值和确定,即椭圆的长半轴和短半轴分别通过求解Xk特征值的平方根得到.

目标形状矩阵服从逆Wishart分布,如式(3),且满足假设1和假设2,而式(5)中,Xk−1的数学期望有如下表达式:

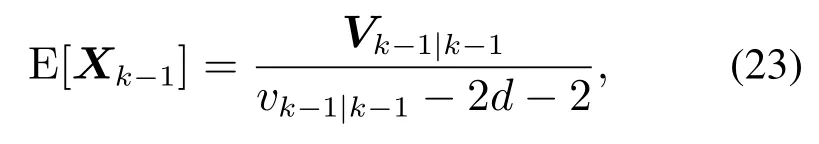
注2该式依据逆Wishart分布的性质进行计算,其证明过程参考文献[31](P113)定理3.4.3.

目标扩展的预测密度为

由于逆Wishart密度的自由度与相应的期望的精度有关,且随着时间间隔T=tk −tk−1的增大而减小,所以引入时间衰减常数τ作为附加的模型参数.

由此,一步预测的Student’s t逆Wishart联合分布和量测似然函数如式(28)–(29):

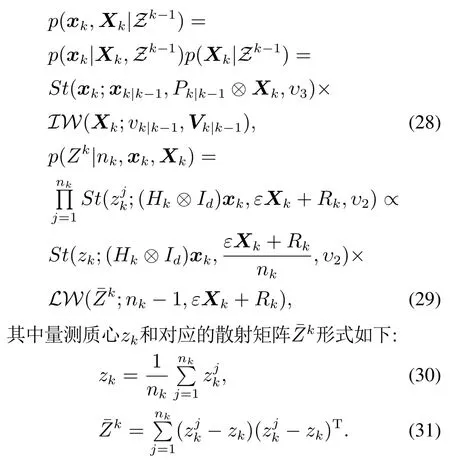
3.2 更新过程

后验概率密度函数有分解形式如下:

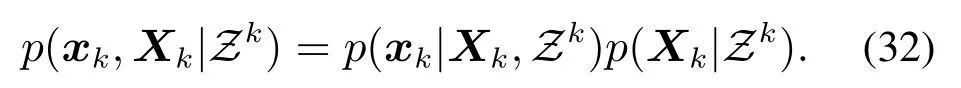
因此需要对目标的运动学状态和形状扩展状态进行更新.

a) 目标运动学更新.

根据贝叶斯滤波公式,需要计算量测似然函数和一步预测概率密度的乘积,由式(28)–(29)可得

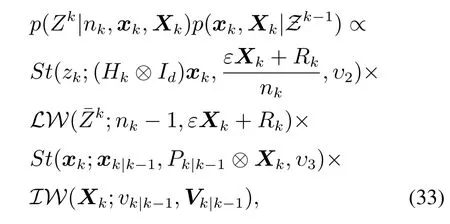
上式需要求解两个Student’s t分布的乘积形式,根据文献[28]引入引理2.

引理2若P和R均为正定矩阵,则有

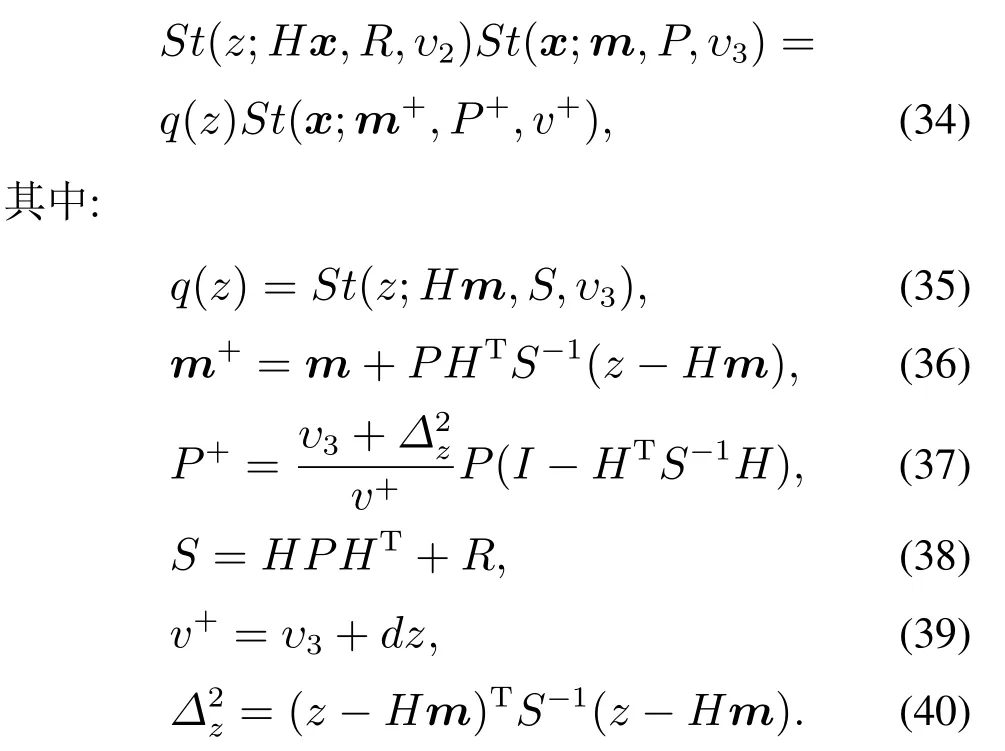
式(38)中的S代表新息协方差阵,式(39)中dz表示量测的维度,表示随机变量zk与其均值向量之间的归一化距离.根据引理2将式(33)中的两个Student’s t分布的乘积计算得到

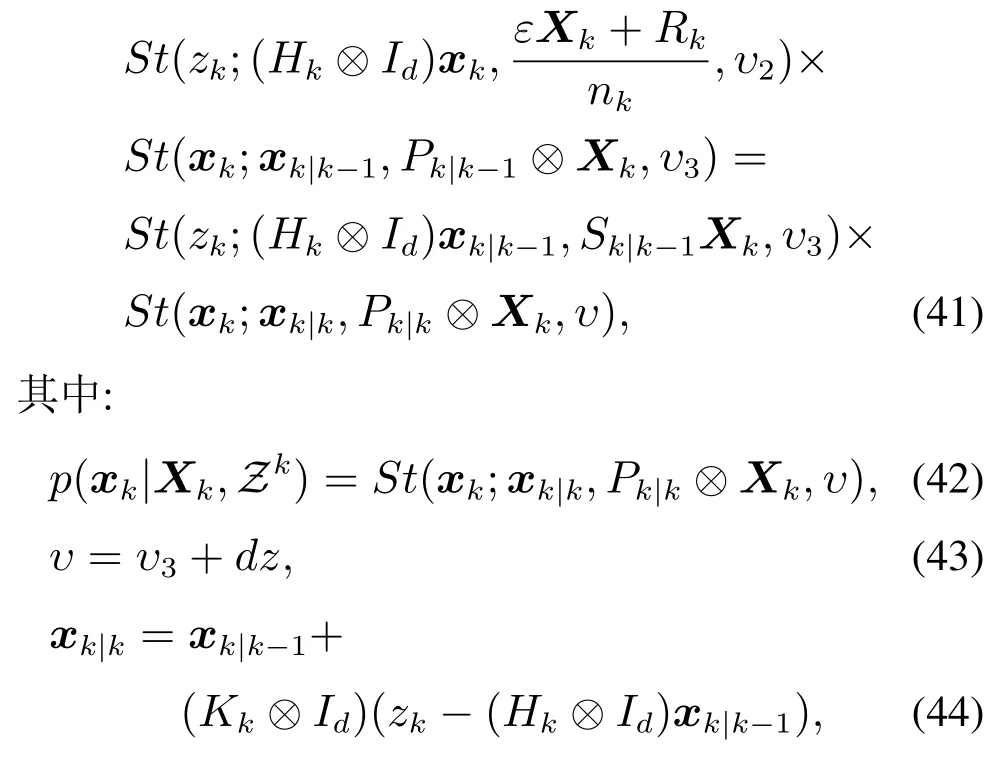
至此,可以得到椭圆扩展目标Student’s t滤波器的后验密度为

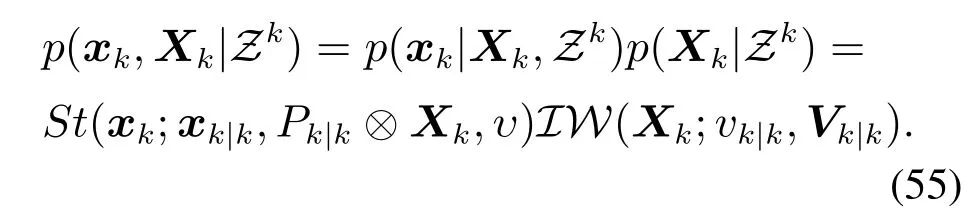
在上述滤波算法的推导过程中,由式(43)可知扩展目标后验概率密度函数中的Student’s t分布的自由度参数υ会随着滤波过程的递推逐渐增大,从而使后验概率分布失去了厚尾特性而退化为高斯分布,导致模型的精度下降,为了保持该滤波器的鲁棒性,需要采用二阶矩匹配的方法对后验概率密度进行修正,即对p(xk,Xk|Zk)中状态向量的后验均值xk|k及协方差矩阵Pk|k进行修正

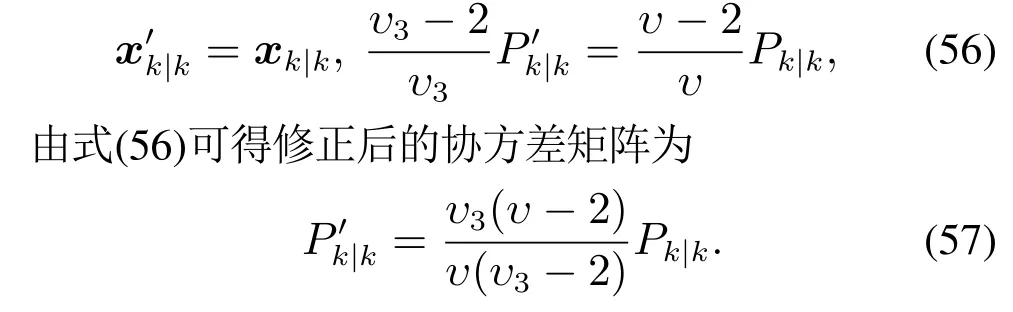
3.3 算法程序伪码

为了说明该算法的具体滤波过程,给出详细的算法伪码:

Algorithm 1 本文算法部分伪码

4 仿真分析

4.1 场景构建

通过对比不同滤波器在异常噪声条件下对椭圆扩展目标的跟踪效果以验证本文所提方法的有效性.本文选取经典的高斯逆Wishart(GIW)滤波器和本文所提出的Student’s t逆Wishart(StIW)滤波器同时对扩展目标进行跟踪.设定系统量测维数dz=2,采样周期T=1 s,总的采样次数N=40,扩展目标采样周期内的量测数目nk服从均值为20的泊松分布.目标的动态演化方程和量测方程如式(2)(7)所示,其中对应的参数Fk|k−1和Hk取值为

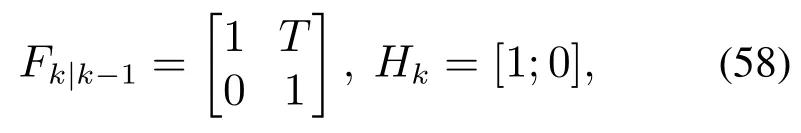
扩展状态的参数初始化为

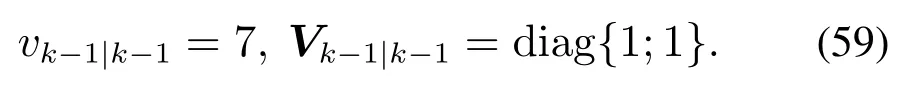
注4本文中的逆Wishart 分布的自由度参数vk−1|k−1的初值依据式(23)确定,本文中d=2,因而需要满足vk−1|k−1>6.

异常的过程噪声和量测噪声可根据下列式子产生

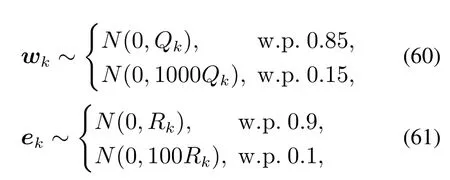
Qk=Dk|k−1⊗Xk,Dk|k−1=µP ×diag{1;1},µP=10−2表示过程噪声系数.Rk=µR×diag{22;22},µR=1表示量测噪声系数.式(59)–(60)表示85%的过程噪声和90%的量测噪声来自协方差为Qk和Rk的高斯噪声,而剩余的15%的过程噪声和10%的量测噪声来自协方差严重增加的Gauss分布,表示异常噪声的拖尾.

4.2 仿真实验1

在过程噪声和量测噪声同时为厚尾噪声条件下,跟踪受异常噪声影响的扩展目标,系统初始状态x0=[30 20 25 30]T,传感器位于坐标原点,其长半轴和短半轴分别为A=10和a=5.采用StIW滤波器和GIW滤波器对扩展目标进行跟踪,并对比二者滤波后目标的质心位置和形状估计的精确性.图4为单次蒙特卡罗仿真实验下得到的两种滤波算法的跟踪轨迹图,可仔细观察得出StIW滤波器能够对目标进行有效的跟踪,这反映了StIW在应对不确定性更高的厚尾噪声环境中的滤波稳定性.

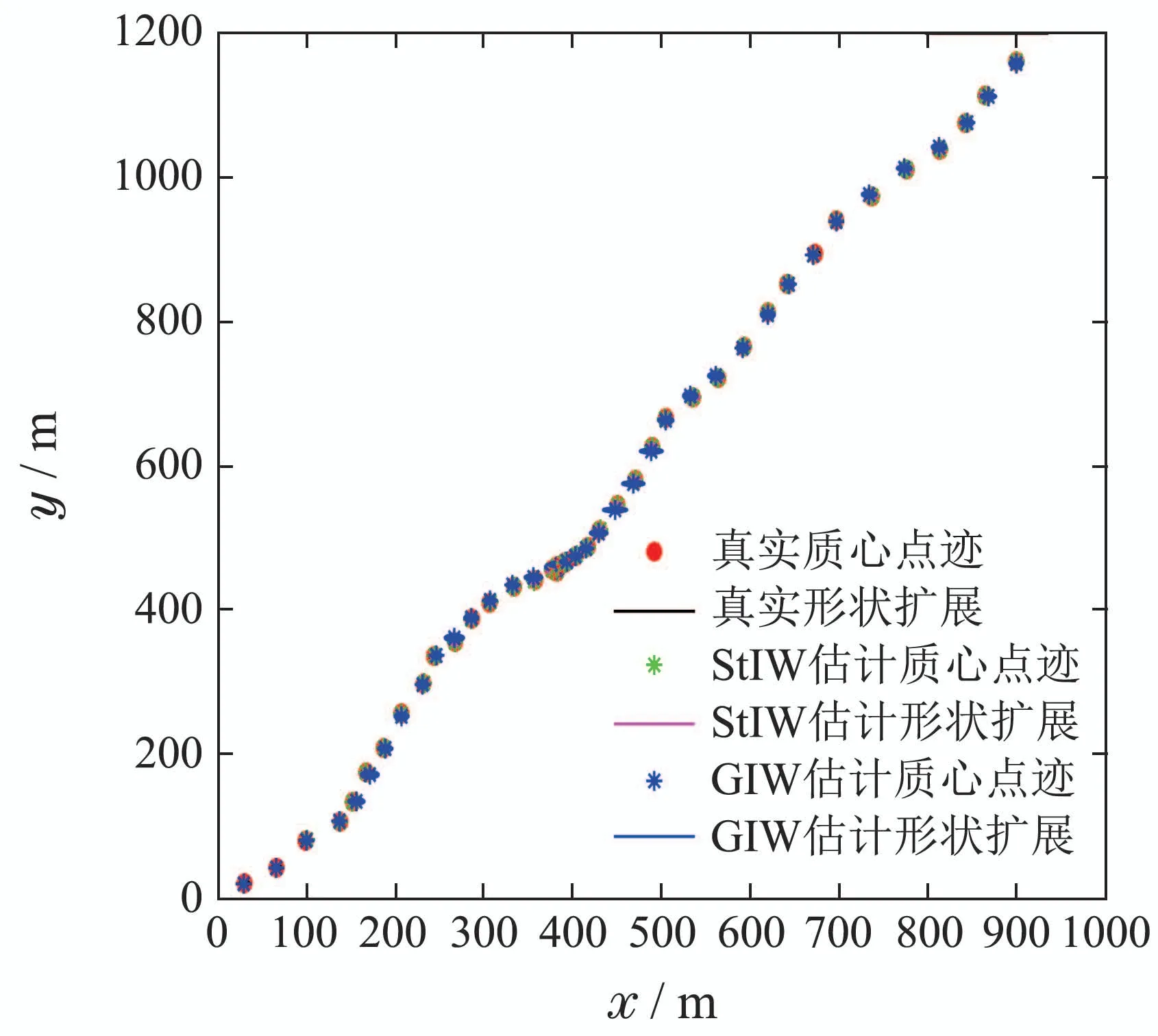
图4 轨迹跟踪图Fig.4 Trajectory tracking graph

为了更清晰的比较两个滤波器的性能,本文给出了如图5所示的目标初始时段(图5(a))、中间时段(图5(b))以及终止时段(图5(c))的两种滤波算法对目标跟踪估计的放大图.可以看出,由于目标轮廓的先验信息未知,虽然两种滤波算法在初始时刻对目标的形状轮廓估计均不大精确,但StIW在最初时刻已经表现出对复杂噪声更好的适应性,呈现出相对更好的估计效果.而随着滤波递推,受到厚尾噪声的持续影响,相较于GIW滤波,StIW滤波器体现出明显的跟踪优势,在更复杂的不确定性环境下呈现出更好的跟踪估计的鲁棒性,不仅对目标的运动学状态估计更加准确,还更为精确地捕捉了目标的形状轮廓信息.

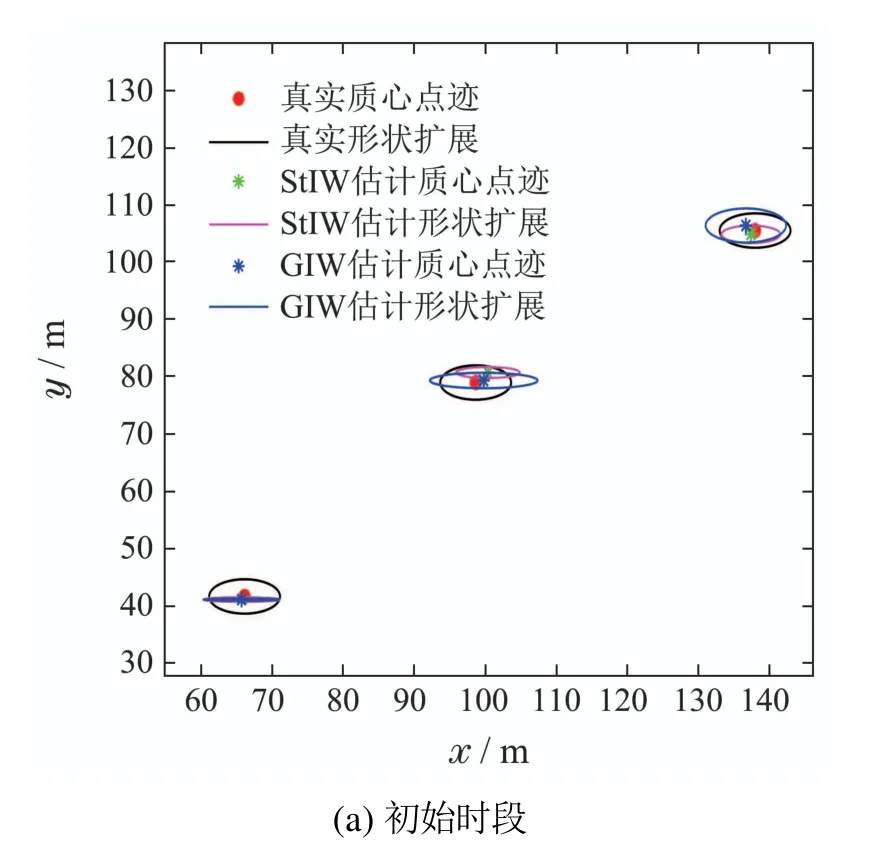
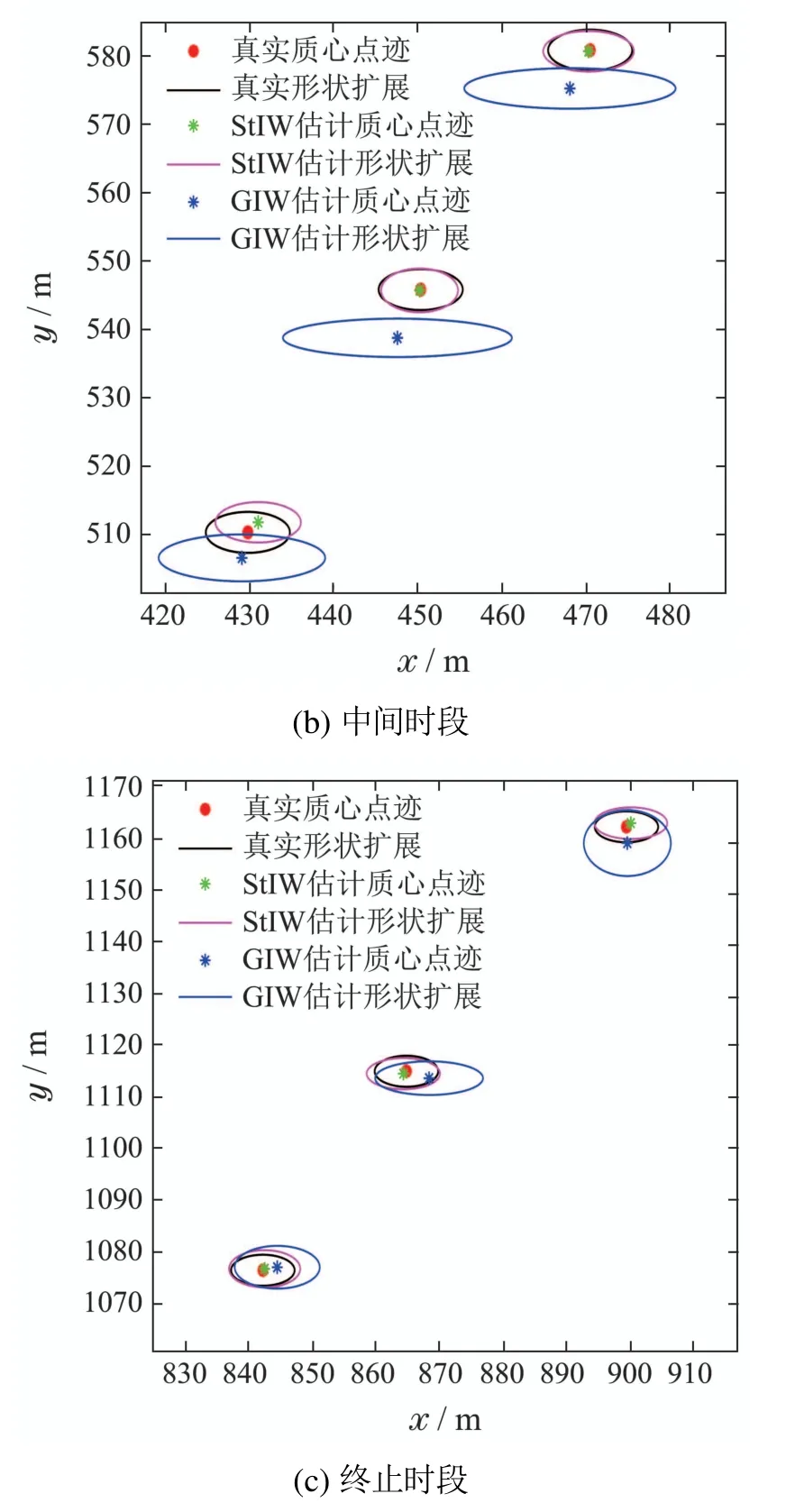
图5 不同时段轨迹跟踪放大图Fig.5 Enlarged view of trajectory tracking at different periods

图6和图7分别为100次独立蒙特卡罗仿真后得到的两种算法对目标的质心位置估计均方根误差和形状长短轴均方根误差的统计值.观察图6可得,本文所提算法的质心估计均方根误差总体最小,由此表明在异常噪声条件下,本文所提算法对扩展目标实时位置的估计更准确.进一步地,由图7可以看出本文算法对目标轮廓的估计更精确,证明本文滤波算法对扩展目标形状估计也更有效.

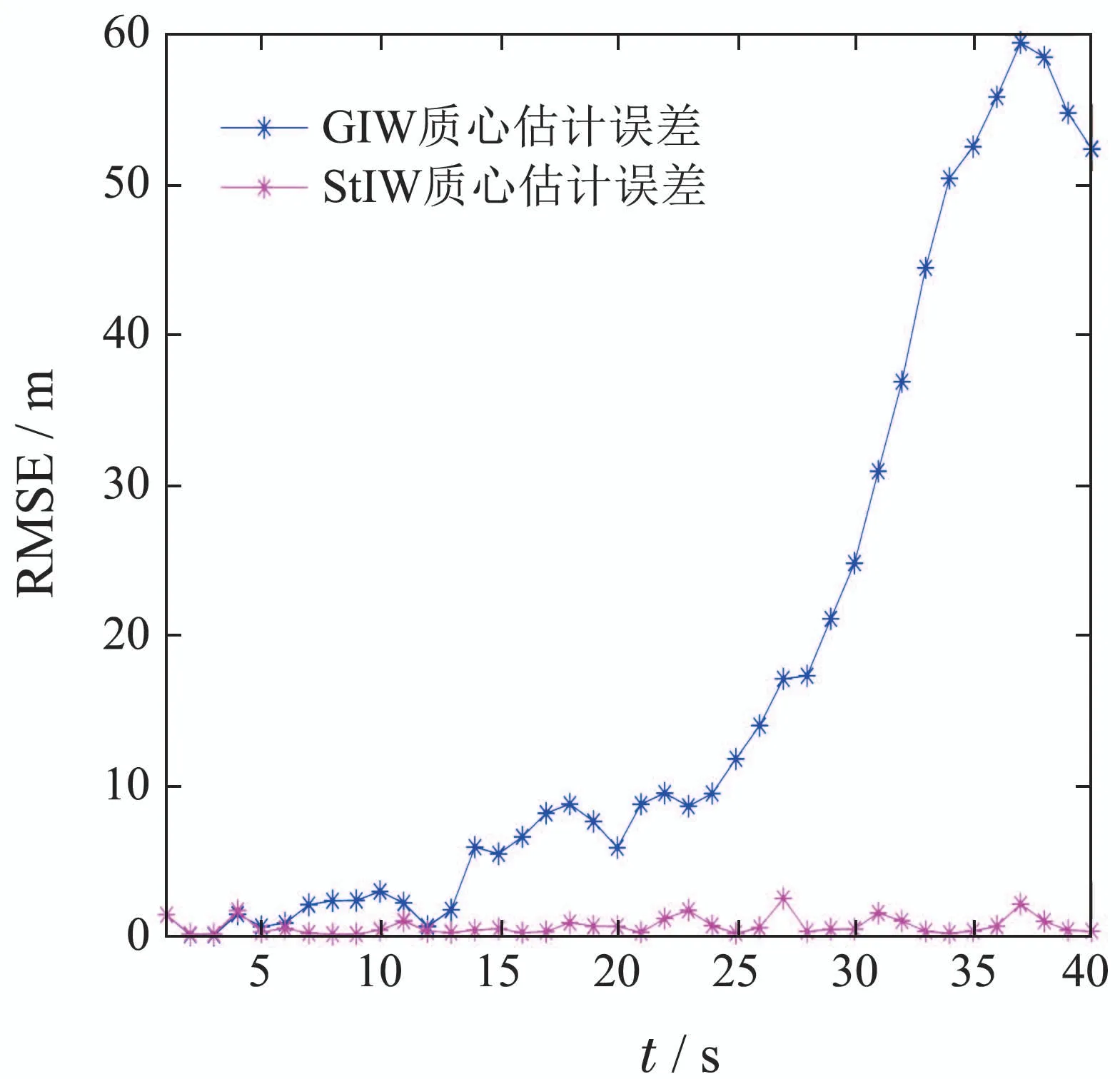
图6 质心位置估计均方根误差Fig.6 Root Mean square error of centroid cosition estimation

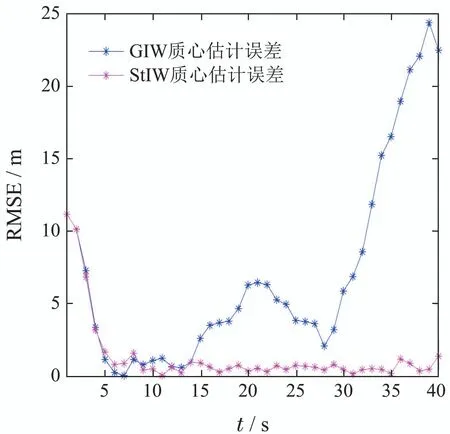
图7 长短轴均方根误差Fig.7 Root mean square error of long and short axis

4.3 仿真实验2

为验证本文所提算法对目标形状动态演变下的鲁棒性和适应性,实验中动态改变椭圆长短轴的大小,椭圆长短轴变化系数coe=1.05,系统初始状态x0=[100 100 150−300]T,椭圆的方向每时刻旋转角度为θ=10°,传感器位于坐标原点,改变过程噪声和量测噪声的系数,同样在式(59)–(60)构造的厚尾噪声条件下利用两种算法对目标运动状态及目标形状轮廓进行估计,令µR=10−2,µP=10−3,从而验证本文所提算法对扩展目标跟踪的有效性.

图8是单次蒙特卡罗实验得到的两种算法对目标形状大小和方向均发生动态改变的目标跟踪轨迹图.观察可得,StIW滤波器仍能对目标实现准确跟踪,显示了StIW在复杂的动态演变跟踪环境下的鲁棒性.

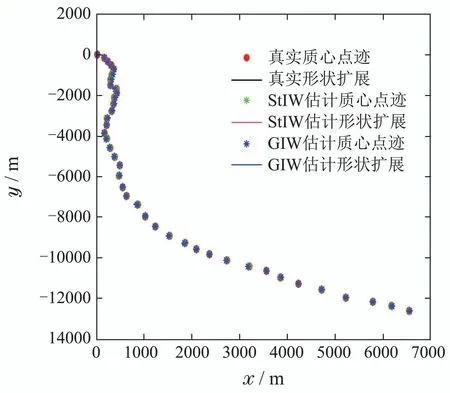
图8 轨迹跟踪图Fig.8 Trajectory tracking graph

为直观体现StIW滤波器的优越性,图9仍然给出了初始时段(图9(a))、中间时段(图9(b))和终止时段(图9(c))对扩展目标的跟踪轨迹放大图.可以看出,无论在跟踪滤波的任何阶段,本文算法在动态演变的扩展形态和方向变化下,相对传统算法都呈现出更加稳定和精确的跟踪估计结果,充分验证了本文算法在异常噪声条件下对扩展目标多重特征估计的有效性.

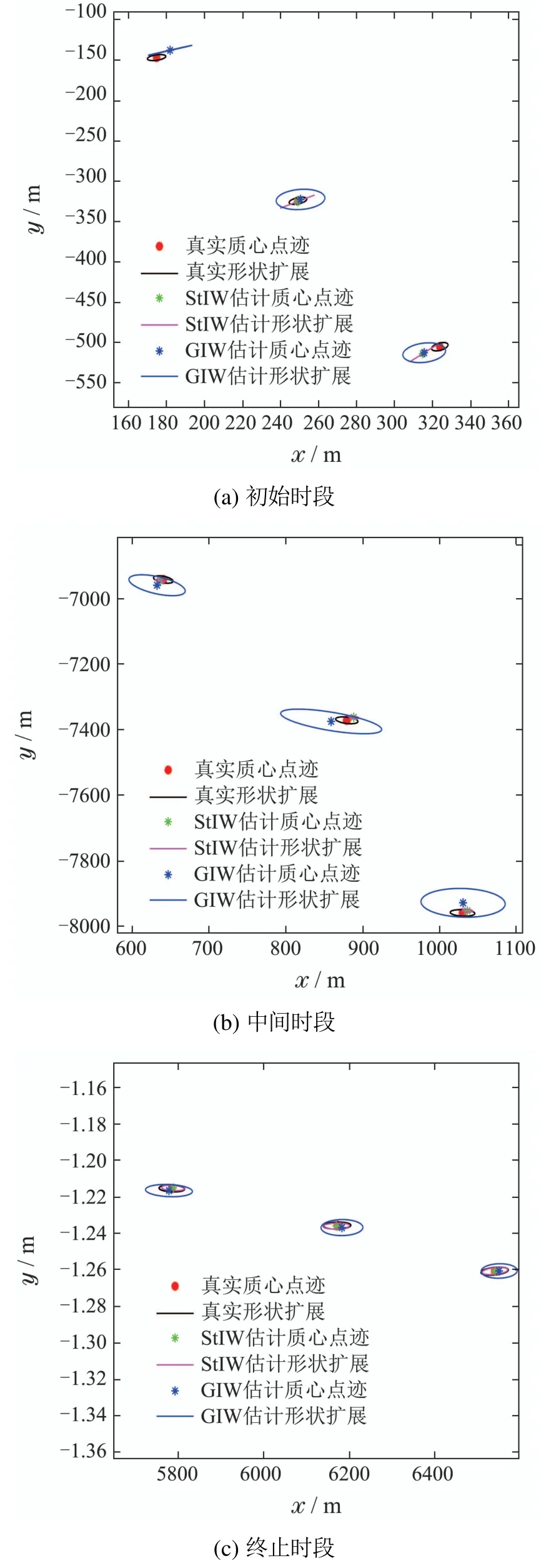
图9 不同时段轨迹跟踪放大图Fig.9 Enlarged view of trajectory tracking at different periods

图10和图11为目标扩展大小和方向发生改变的情况下,100次蒙特卡罗仿真实验得到的目标质心位置估计和形状长短轴估计的均方根误差的统计值.观察图10可得,StIW滤波算法对扩展目标的质心估计均方根误差较小,验证了StIW对运动目标定位的相对准确性.图11显示StIW算法也能在复杂异常噪声影响下,更加准确的估计出随时间动态演变的目标形状轮廓特征,这对于目标的深度识别无疑具有极其重大的现实意义.

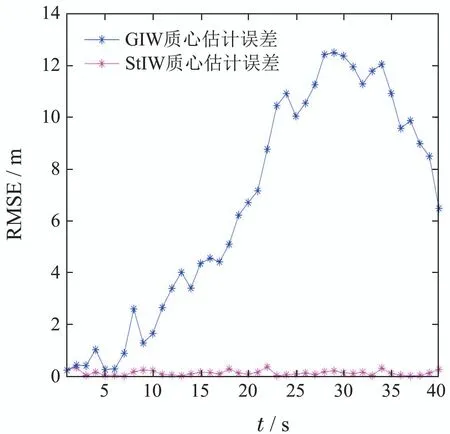
图10 质心位置估计均方根误差Fig.10 Root mean square error of centroid position estimation

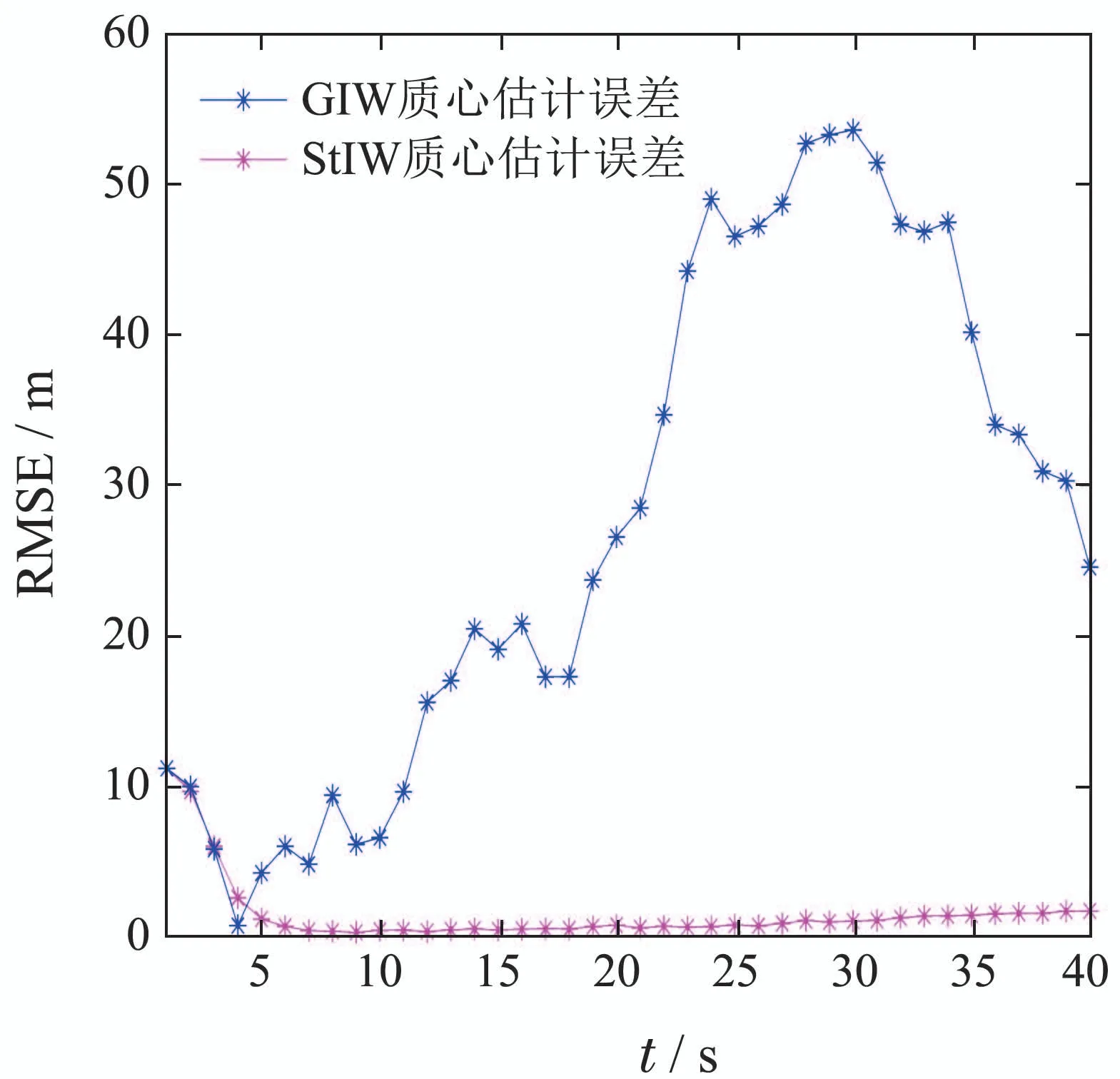
图11 长短轴均方根误差Fig.11 Root mean square error of long and short axis

5 结论

本文主要创新点是针对异常噪声条件下扩展目标跟踪问题,提出了一种基于鲁棒自适应扩展目标StIW跟踪滤波算法,经过多重仿真实验的论证分析,充分验证了本文所提算法的有效性.在今后的研究中,本文算法还可以通过多目标递推滤波器扩展到多扩展目标跟踪领域,对于更为复杂的跟踪环境将具有更加广阔的应用前景.