基于功能性电刺激的上肢康复系统条件反馈控制

吴振龙 ,霍本岩 ,秦云辉 ,刘艳红 ,李东海

(1.郑州大学电气工程学院,河南郑州 450001;2.清华大学电力系统国家重点实验室,北京 100084)

1 引言

根据最新的全球疾病负担研究数据显示,我国公民发生脑卒中的风险为39.9%,位居世界第一位[1].2019年我国卒中患者超过两百万,其中很多抢救成功患者会有不同程度的致残后遗症[2].由于我国康复医疗资源严重短缺,患者缺乏专业有效的康复训练,面临着肌肉萎缩甚至终生残疾的风险.功能性电刺激(functional electrical stimulation,FES)由于其在肌肉锻炼以及神经通路功能恢复方面的优势,引起了医疗科研人员越来越广泛的关注[3–4].

随着电刺激相关技术的发展,FES技术研究从被动型的开环刺激逐渐发展为主动型的闭环刺激[5].基于FES的闭环刺激是通过对肌肉施加适当的电刺激信号实现人体肌肉的周期性动作或者日常动作的康复性锻炼.在实现上述动作时,反馈控制器需要根据反馈信号更新刺激强度,为了保证康复动作的准确性,反馈控制器需要能够准确计算刺激的强度.然而,人体肌肉的动态模型存在着强非线性、多源扰动、模型不精确和参数变化大等特点,会造成反馈控制性能的下降.上述人体肌肉的动态特性要求反馈控制器具有强扰动抑制能力.为了提高基于FES的人体康复系统的跟踪精度和扰动抑制的能力,弱模型和强模型的控制策略已经被应用到基于FES的康复系统研究.

弱模型控制策略主要包括经典比例–积分–微分(proportional-integral-derivative,PID)控制、滑模控制以及鲁棒控制等策略.文献[6]针对腕部病理性震颤设计了PID控制器,并在搭建的康复系统中进行了实验验证.尽管PID控制器具有简单的结构与可靠的性能,并广泛应用在几乎所有的工业系统中,然而其控制能力受到自身误差反馈结构的限制[7].滑模控制和切换滑模控制也应用在基于FES的康复系统中[8–9],并分别进行了仿真与实验验证,其中文献[9]的实验数据表明,SSMC能够在每分钟50转的期望轨迹上实现每分钟转数的平均步频跟踪误差.为应对人体肌肉动态模型的不确定性,H∞控制和切换H∞控制也分别应用在功能性电刺激循环控制中[10–11],实验数据表明上述控制策略能够有效减低步频跟踪的误差,文献[10]中基于帕金森病患者的实验数据表明步频跟踪误差由原来的0.43±4.06 转/分降低到0.17±3.11转/分.由于上述控制策略具有较大的计算量和工程实现难度大等特点,在实际应用时受到一定的限制[12].为增强康复系统的鲁棒性,文献[13]提出了一种非线性自抗扰控制方案,并在基于FES的上肢康复系统对多位实验者进行了实验,实验数据表明非线性自抗扰控制能够很好的跟踪输出力的设定值.然而,非线性自抗扰控制实现复杂、参数整定困难,限制了其工程实际应用.

强模型控制策略设计主要围绕建模与模型预测控制研究,文献[14]针对膝关节伸展的控制问题,提出了一种基于梯度投影的模型预测控制策略,通过Lyapunov函数作为终端成本,保证了控制系统的稳定性.文献[15]针对FES电动自行车的跟踪目标提出了自适应控制并完成了实验验证.由于MPC的设计依赖于肌肉的精确动态模型,然而神经肌肉的精确动态模型由于肌肉的复杂性难以建立,造成控制效果不理想.

此外,还有其他先进控制策略,如数据驱动控制[16](data-driven control,DDC)、重复学习控制[17–18]、迭代学习控制[19–20]和反馈线性化[21]等也分别被尝试应用在基于FES的康复系统中.但上述算法在临床推广时会受模型、实施平台、计算量等因素的限制.

基于条件反馈的比例–积分控制(conditional feedback proportional-integral,CF–PI)具有控制效果好、工程实现容易、整定参数少、整定规则简单等优点[22].CF–PI能够将跟踪控制与扰动抑制转化为两个独立环节分别进行设计,实现跟踪与抗干扰的完全分离.本文针对FES上肢康复系统的强非线性、多源扰动、模型不精确和参数变化大等控制难点,提出一种CF–PI控制策略,并给出简单、有效的控制器参数整定方法.在基于FES的上肢康复系统实验平台上针对不同实验者在不同目标输出力下进行了实验验证,并与经典PI控制效果进行对比,实验结果表明所提的CF–PI在保证闭环系统鲁棒性的条件下具有更好的跟踪和抗干扰性能.本文的主要创新点包括:

1) 针对基于FES的上肢康复系统提出了CF–PI的控制策略;

2) 提出了一种适用于CF–PI的实用有效的参数整定方法;

3) 所提方法的有效性在基于FES的上肢康复系统控制平台上进行了验证.

全文内容安排如下:第2节介绍了基于FES的上肢康复系统和肌肉建模;基于条件反馈的比例–积分控制策略及参数整定方法在第3节中进行介绍;第4节通过仿真与实验验证了所提方法在基于功能性电刺激的上肢康复系统中的有效性;第5节对全文进行总结.

2 上肢康复系统实验平台与建模

2.1 上肢康复系统实验平台

基于FES的上肢康复系统控制平台的结构如图1所示.该系统硬件平台主要包括控制器、多通道刺激器、电极片、多维力传感器和传感器变送器等.控制器为NI公司研发生产的myRIO控制器,通过LabVIEW将设计的控制策略下装到控制器中.多通道刺激器将控制器输出的PWM控制信号转化为进入电极片的信号.电刺激信号施加在实验者上肢肌肉,其中电极片的正极贴在肱二头肌上,负极贴在肱二头肌肌腱处,使得肌肉根据电刺激信号变化进行调整,并通过固定在小臂末端的多维力传感器测得肌肉的输出力.经过传感器变送器将输出力信号转化为电压信号送入控制器,根据控制策略进一步调整控制器输出PWM信号.此外,控制器与多通道刺激器均需要电源供电.更加详细的平台介绍见文献[13].

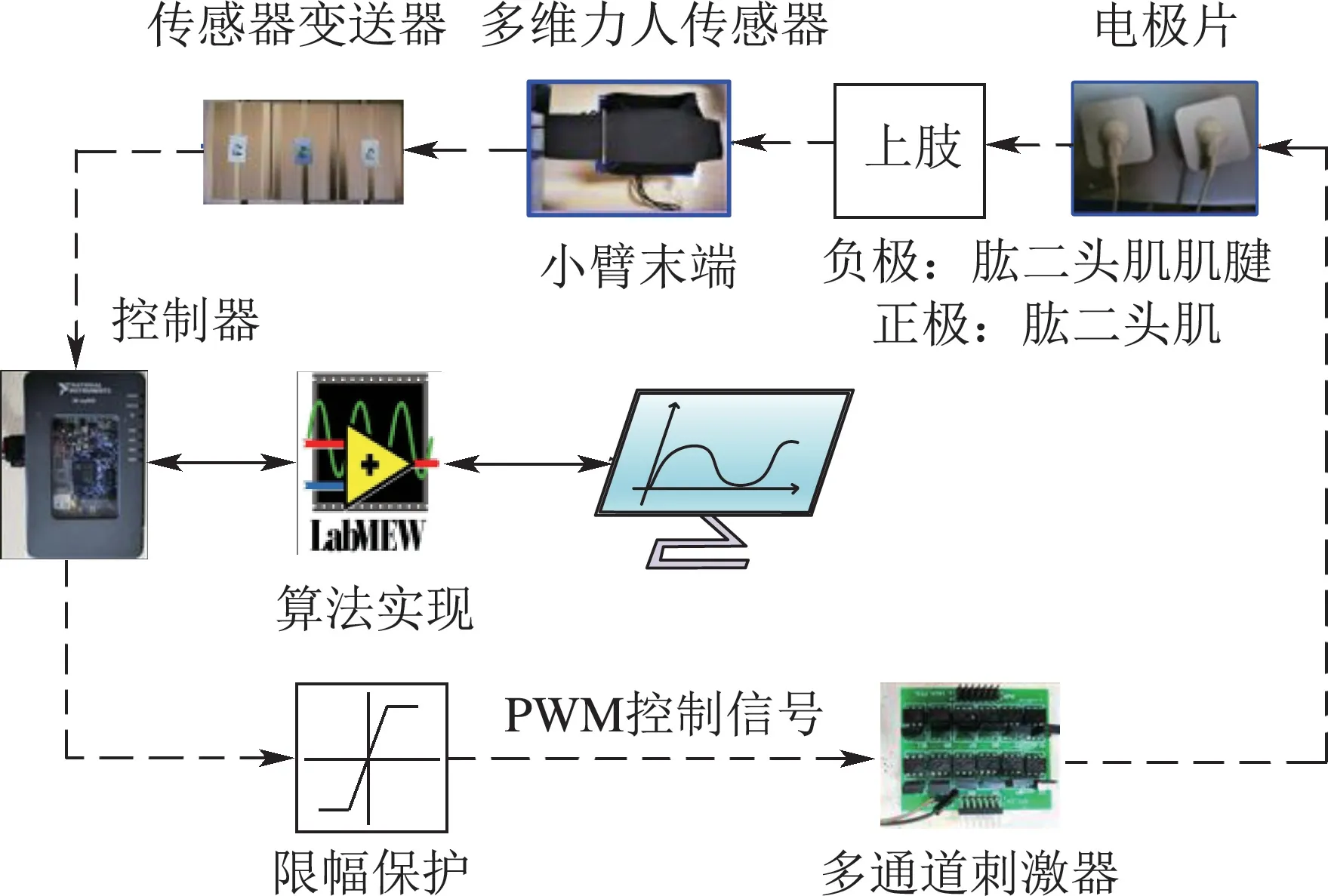
图1 上肢康复系统的控制结构图Fig.1 The control structure of the upper limb rehabilitation system

2.2 肌肉模型

在FES过程中,肌肉的特性会发生较大的变化,并且上肢肌肉特性也因人而异.这使得建立基于动力学的精确数学模型是非常困难的.Hammerstein模型采用线性传递函数和非线性函数分别描述肌肉动力学的线性部分和非线性部分.该方法能够实现简单有效、易辨识的方式表征肌肉动态特性,在肌肉建模中有广泛的应用.Hammerstein模型通过静态非线性块与动态线性块的串联方式表征被控系统的动态特性如图2所示,其中f(u)为电刺激下肌肉静态非线性,即等长招募曲线(isometric recruitment curve,IRC),Gp(s)为线性肌肉动态特性,即线性激活动态(linear activation dynamics,LAD).

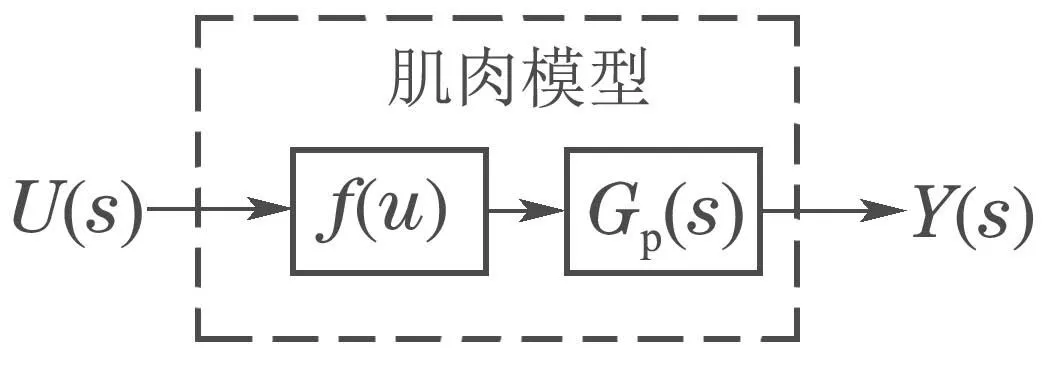
图2 Hammerstein模型结构Fig.2 The structure of Hammerstein model

根据Hammerstein模型定义,IRC采用多项式函数代替迟滞的正弦特性,f(u)的表达式为

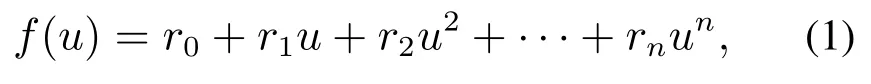
其中:r0,r1,···,rn为多项式的系数,n为多项式的阶次.阶次的选择可以根据模型与实际数据的拟合程度选择,基于文献[11]分析可知,n=3能够保证很好的拟合效果,本文也采用n=3进行拟合.

由于肌肉在受到电刺激时,肌肉内钙离子响应需要一定的时间,即输入与输出之间存在一定的延迟,因此采用含有延迟的传递函数描述LAD,Gp(s)的形式为

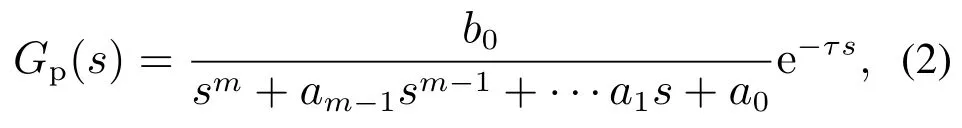
其中:b0为Gp(s)的分子多项式系数,a0,a1,···,am−1为Gp(s)的分母多项式系数,m为传递函数的阶次,τ为延迟时间常数.Gp(s)的阶次与模型的精度成正比,阶次与控制器设计难度成反比,综合权衡本文采用m=2.τ根据开环实验时系统的输入和输出响应差异得到,其他参数可以通过最小二乘法辨识得到.

通过开环实验,输入周期为8 s 的正弦预期信号,基于输出数据可得Hammerstein模型如下:

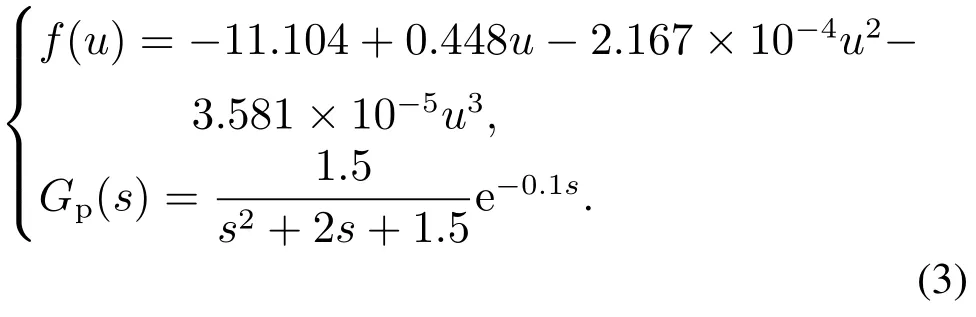
需要说明的是,该模型是基于第1个实验者的实验数据建立的,这是由于第1个实验者经历过较长的电刺激,其肌肉模型能够较好地模拟康复者长期功能性电刺激后的肌肉特性,具有较好的代表性.虽然不同实验者的模型参数会有一定的变化,但为便于工程应用,将采用该模型作为标称模型进行控制器设计与参数整定.

在相同激励下系统输出与Hammerstein模型的输出对比如图3所示.由图3可知所建立的Hammerstein模型能够很好地反映肌肉的动态特性.虽然存在模型误差,但可以通过设计合适的控制策略予以补偿.

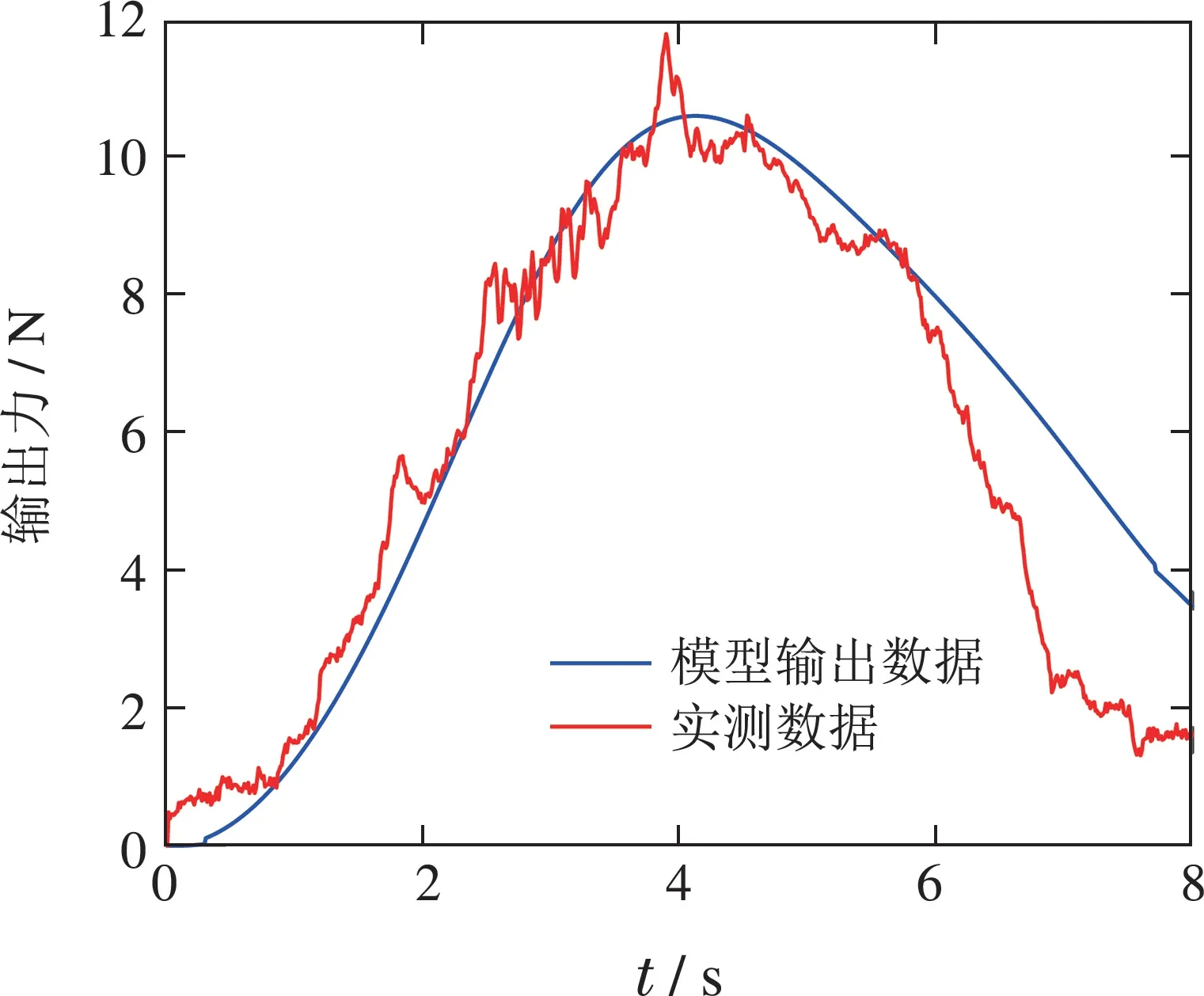
图3 相同激励下实际系统输出和Hammerstein模型输出Fig.3 The outputs of the real system and the Hammerstein model with the same stimulation

3 基于条件反馈的比例–积分控制策略

3.1 CF–PI原理

CF–PI作为一种二自由度控制(two degree of freedom control,TDOFC)结构,能够实现跟踪性能与抗干扰性能的独立设计:跟踪性能取决于CF–PI中参考模型的响应特性,模型的不确定性和扰动抑制性能取决于CF–PI中PI控制器.以辨识的二阶惯性加纯延迟的被控制对象为例,设计的CF–PI如图4所示,其中Gp(s)为二阶惯性加纯延迟的被控制对象,其传递函数为

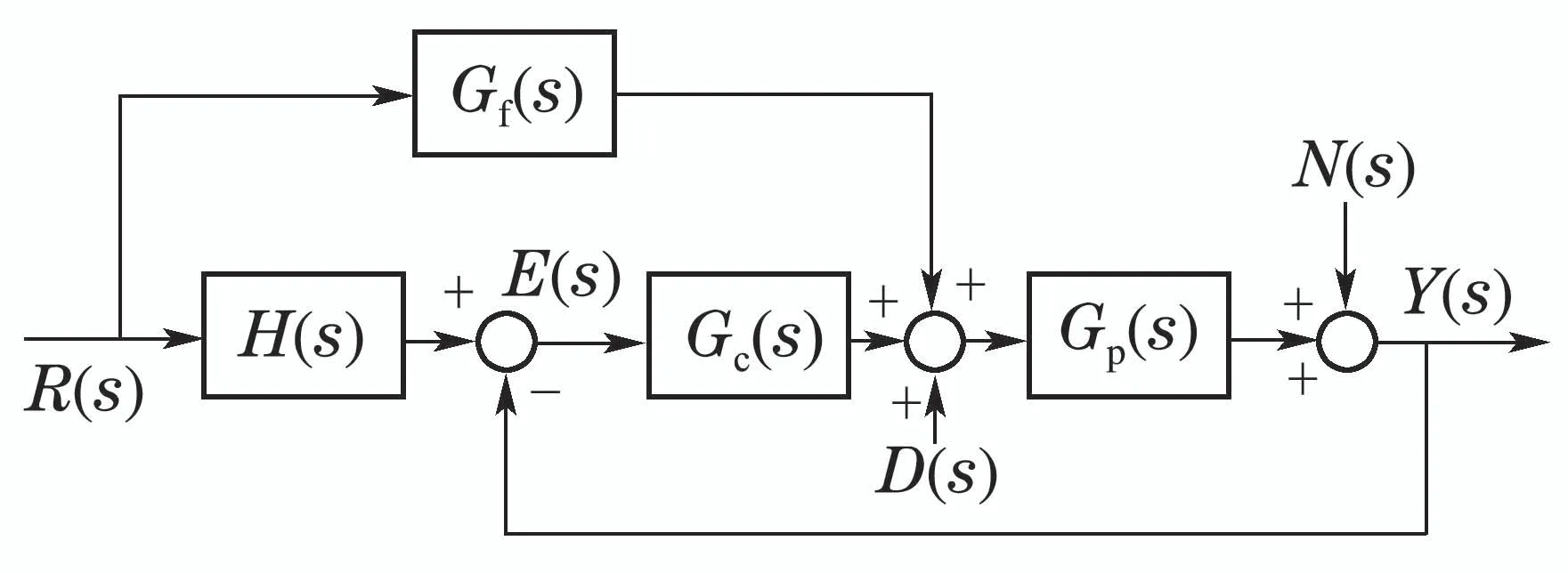
图4 CF–PI的控制结构Fig.4 The control structure of CF–PI

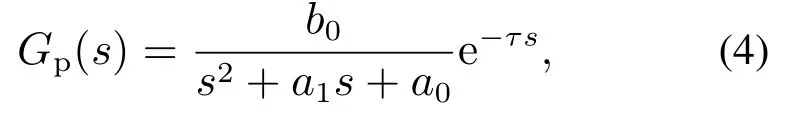
H(s)为预期动态方程,从阶次匹配的角度考虑,预期动态方程的阶次与被控制对象的阶次相同.为简化设计,H(s)一般采用如下形式

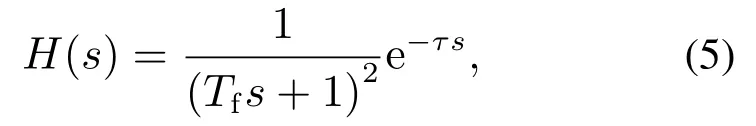
其中Tf为预期调节时间常数.

根据图4,从设定值R(s)到系统输出Y(s)的闭环传递函数为

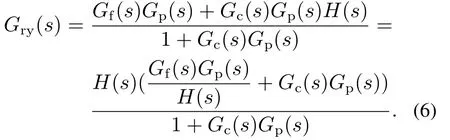
当Gf(s)Gp(s)/H(s)=1,即Gf(s)=H(s)/Gp(s)时,可以得到设定值到系统输出的闭环传递函数

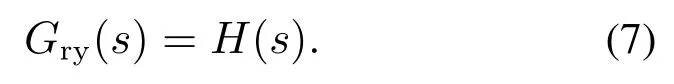
可知在理想情况下,闭环系统的跟踪性能完全取决于预期动态方程.

此时,闭环系统的输出

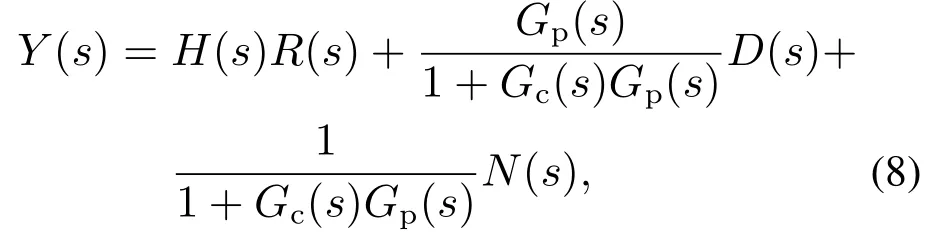
其中D(s)和N(s)分别为输入扰动和测量噪声.由式(8)可知,扰动抑制的能力仅取决于Gc(s).闭环系统的特征方程为1+Gc(s)Gp(s)=0,即前馈不影响系统的稳定性.通过等价变化,可以得到CF–PI的TDOFC结构如图5所示.

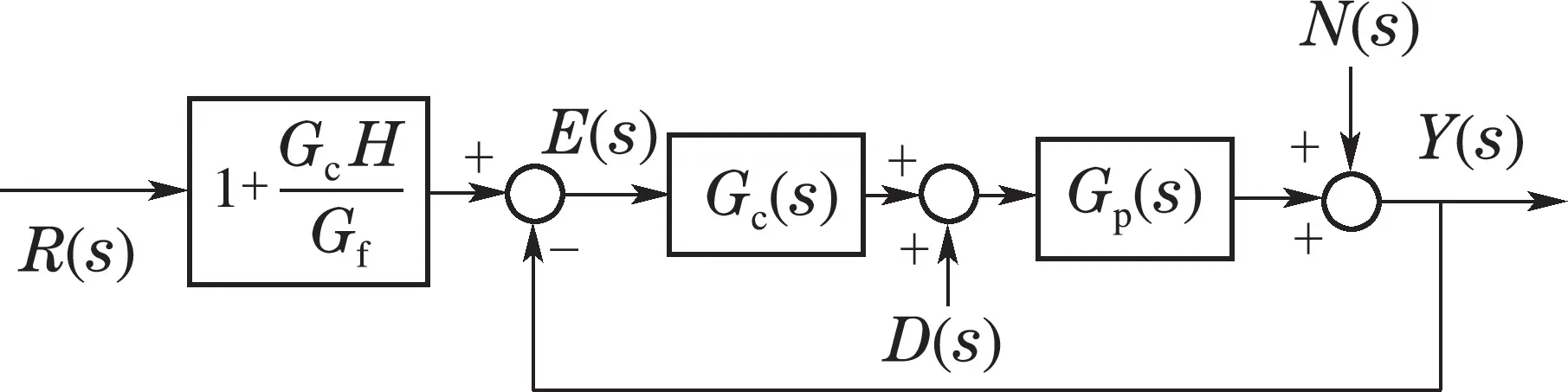
图5 CF–PI的二自由度等价形式Fig.5 The equivalent structure of TDOFC for CF–PI

由于微分作用会放大测量噪声会加快肌肉的疲劳,为抑制噪声对于控制量的方法,反馈控制器Gc(s)选择为PI控制器

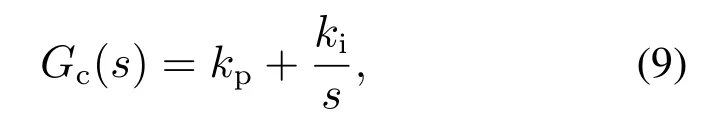
其中kp和ki分别为反馈控制器的比例增益与积分增益.

为进一步简化Gc(s)的参数整定,本文提出一种简化的参数整定方法:

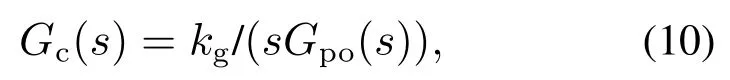
其中Gpo(s)为Gp(s)的非延迟部分,即

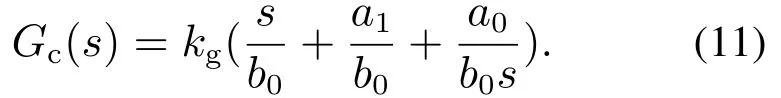
由于反馈控制器Gc(s)为PI控制器,微分项可以忽略,即可以得到Gc(s)的形式为

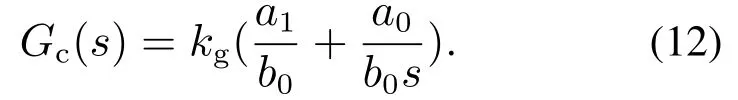
即反馈控制器Gc(s)通过调节kg的值来改变PI参数.综上所述,可知CF–PI需要整定的参数为{Tf,kg},下面针对上肢康复系统,通过单一变量法对上述参数对控制效果的影响进行分析,并进而给出CF–PI的实用有效的参数整定方法.

由于建立的Hammerstein模型含有非线性部分,可以通过设计非线性补偿部分f−1(u)将非线性部分补偿.综上所述可以得到适用于基于FES的上肢康复系统的含非线性补偿的CF–PI控制结构如图6所示.此时,基于FES的上肢康复系统中已知的非线性部分通过f−1(u)进行补偿,闭环系统的跟踪性能由预期动态方程H(s)来决定,系统的不确定性与扰动抑制通过反馈控制器Gc(s)进行调节.

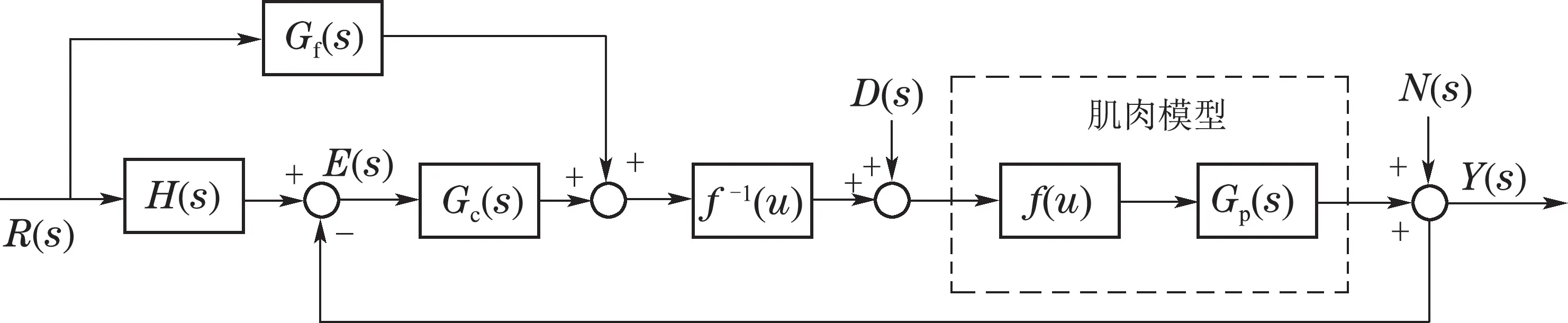
图6 提出的控制结构Fig.6 The proposed control structure

3.2 CF–PI参数整定

为了分析控制器参数变化对系统性能的影响,针对式(3)中的模型,对已经整定的CF–PI的参数{Tf=0.4,kg=0.75},通过单一变量法,在保持kg(Tf)不变的时候逐渐改变Tf(kg)的值,可以得到图7和图8所示的仿真结果.

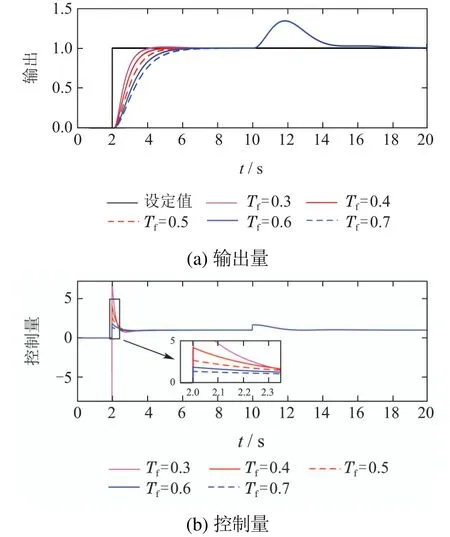
图7 不同Tf下的系统响应Fig.7 The system response with different Tf

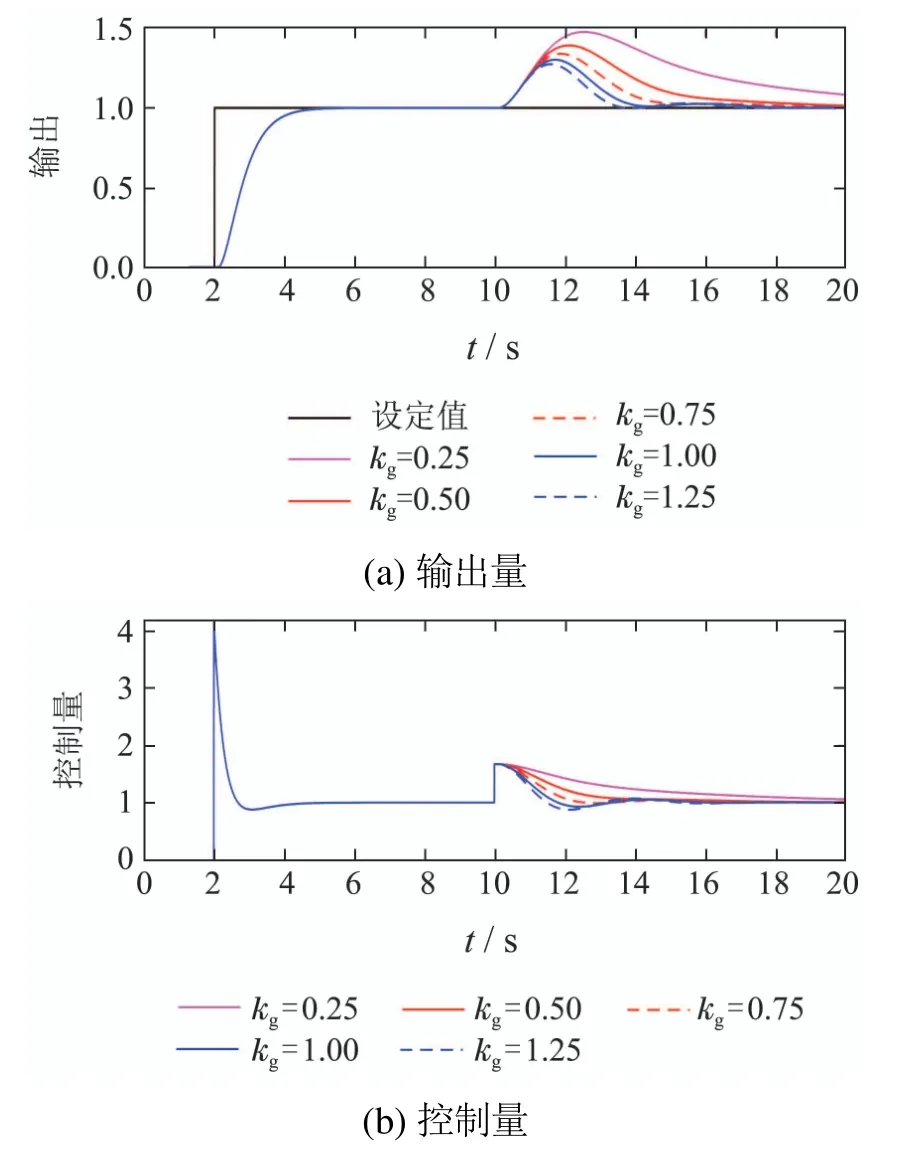
图8 不同kg下的系统响应Fig.8 The system response with different kg

从图7可知,随着Tf的减小,闭环系统的跟踪速度逐渐加快,但控制量的变化越来越剧烈,如图7(b)所示,这会让患者或者实验者产生肌肉灼伤的感觉.因此Tf的选择不宜过快,需要根据肌肉特性来选择合适的值.从图8可知,随着kg的增加,闭环系统的抗干扰能力逐渐增加.然而闭环系统的鲁棒性会随着kg的增加而变弱.为了更好的说明这个问题,采用常用的最大灵敏度函数Ms作为闭环系统鲁棒性的衡量指标[22]

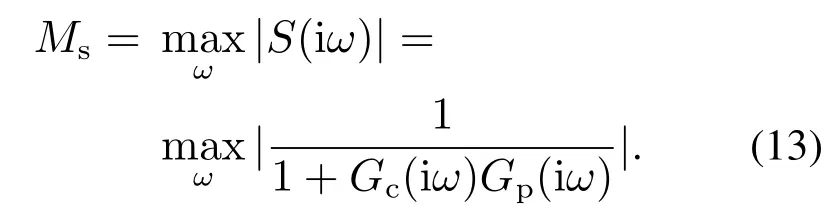
根据式(13)可得Ms随kg变化的曲线如图9所示.由图9可知Ms和kg负相关,故kg的值应该考虑鲁棒性的约束,即满足Ms∈[1.2,2.0]的约束[22].

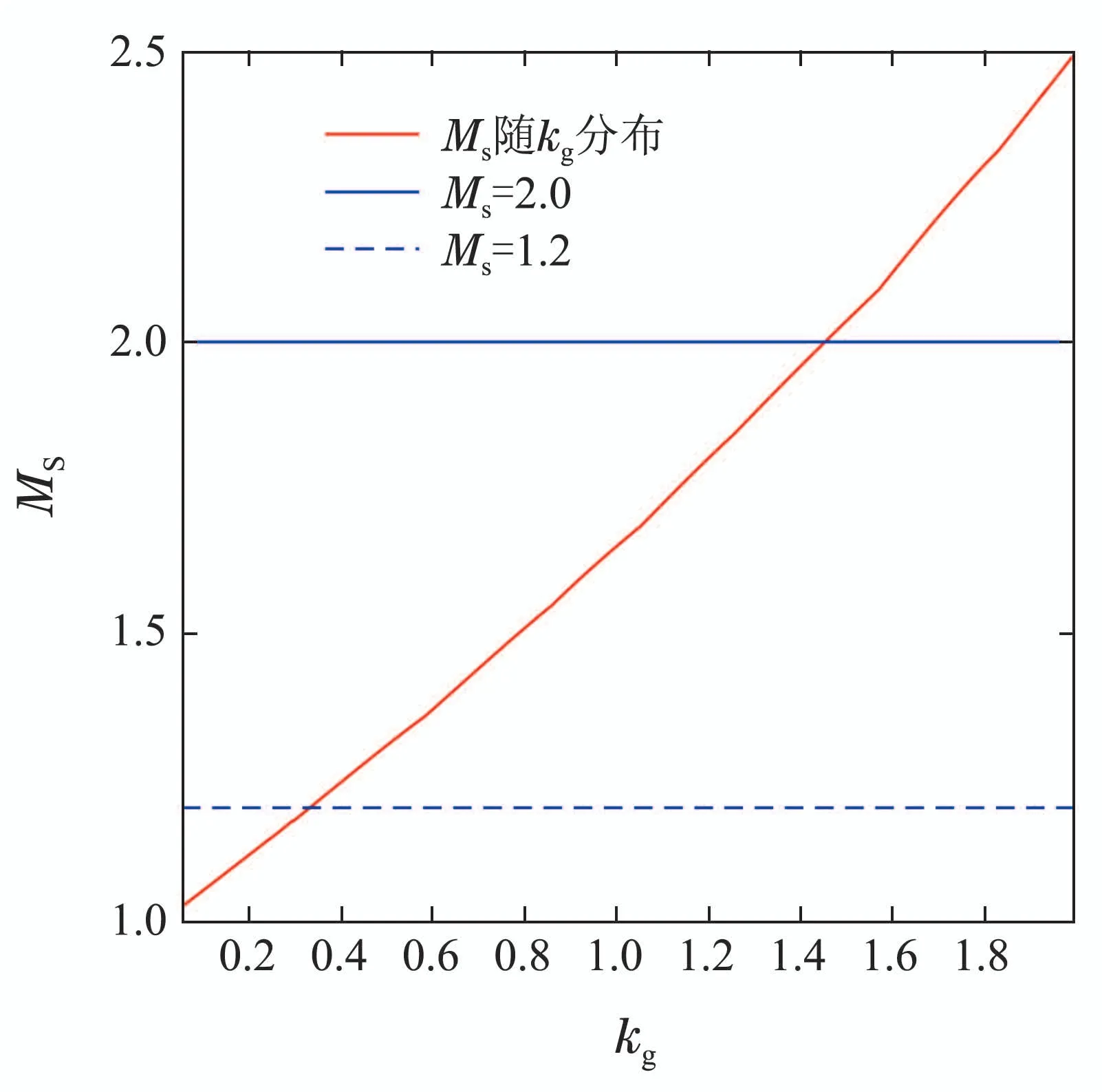
图9 Ms在不同kg时的分布Fig.9 The distribution of Ms with different kg

需要说明的是,随着Tf的变化,闭环系统的抗干扰性能未发生明显的变化,同理随着kg的变化闭环系统的跟踪性能未发生明显的变化,可知CF–PI能够将跟踪与抗干扰完全分离进行设计.

综上所述,根据跟踪速度的要求选择CF–PI中Tf的值,kg的选择需要满足Ms∈[1.2,2.0]的约束,根据大量仿真总结,kg的推荐范围为kg∈[0.4,1].

4 仿真和实验验证

4.1 仿真验证

根据上节中CF–PI的参数整定规则,针对式(3)中的Hammerstein模型,可以选择CF–PI的参数为{Tf=0.4,kg=0.75},即kp=1,ki=0.75和Tf=0.4.选择基于Skogestad 内模控制(Skogestad internal model control,SIMC)整定的PI控制器[23](SIMC–PI)和文献[24]中的DDC控制器作为对比,通过将式(3)中Gp(s)近似为一阶惯性加纯延迟对象,即

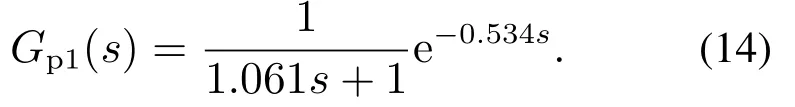
在保证相同鲁棒性约束的前提下得到SIMC–PI的参数,即kp=0.80和ki=0.755.需要说明的是选择SIMC的原因是因为SIMC被认为是在工业应用中最有效的PI控制器参数整定规则[23].基于PID的DDC的详细设计方法见文献[24],其参数设置如下:参考模型取1/(0.4s+1)2,PID的初始参数为kp=1,ki=0.75和kd=0.2,参数的学习因子分别为ηp=0.5,ηI=−0.01和ηD=0.3,信息向量的阶次为ny=3和nu=6.

基于设计的CF–PI,SIMC–PI和DDC以及式(3)中的Hammerstein模型,结合非线性部分补偿可以得到阶跃设定值下的仿真结果如图10所示,从图中可知CF–PI和SIMC–PI具有类似的抗干扰性能,DDC在抗干扰性能上有一些优势,而跟踪性能介于CF–PI和SIMC–PI之间.此外,CF–PI,SIMC–PI和DDC的误差绝对值积分(integral of absolute error,IAE)指标分别为1.82,2.35和2.44,CF–PI的IAE指标分别为SIMC–PI和DDC的77.5%和74.6%,故本文所设计的控制器在保证鲁棒性能的条件下,具有更高的跟踪精度.

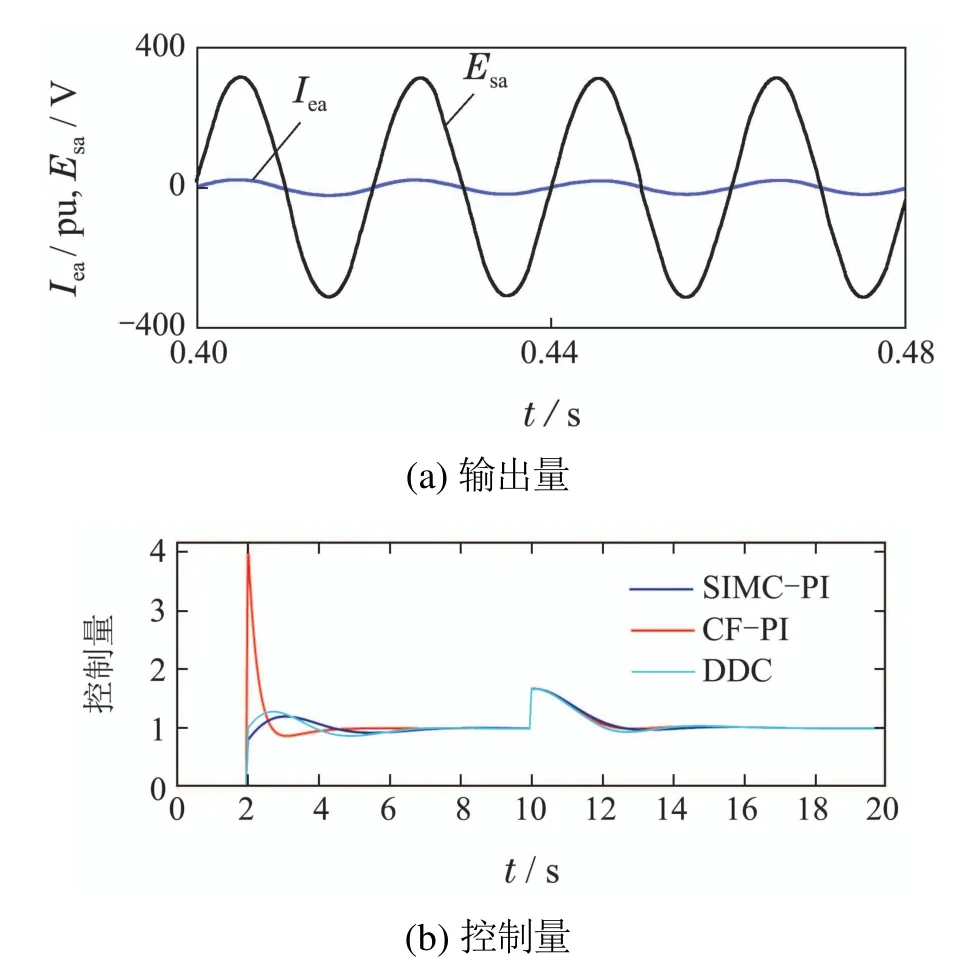
图10 不同控制器作用时阶跃响应下的仿真结果Fig.10 The simulation result of step response with different controller

为了分析CF–PI和SIMC–PI跟踪时变信号的能力,目标输出力采用周期为2πs、幅值为1的正弦信号,仿真结果如图11所示.从图中可知,CF–PI的跟踪速度更快,而DDC的跟踪性能随着时间的推移逐渐下降.CF–PI,SIMC–PI和DDC的IAE指标分别为9.88,14.49和13.22,即CF–PI的IAE指 标 只 有SIMC–PI的68.2%和74.7%,可见CF–PI在面对正弦信号跟踪时具有明显优势.

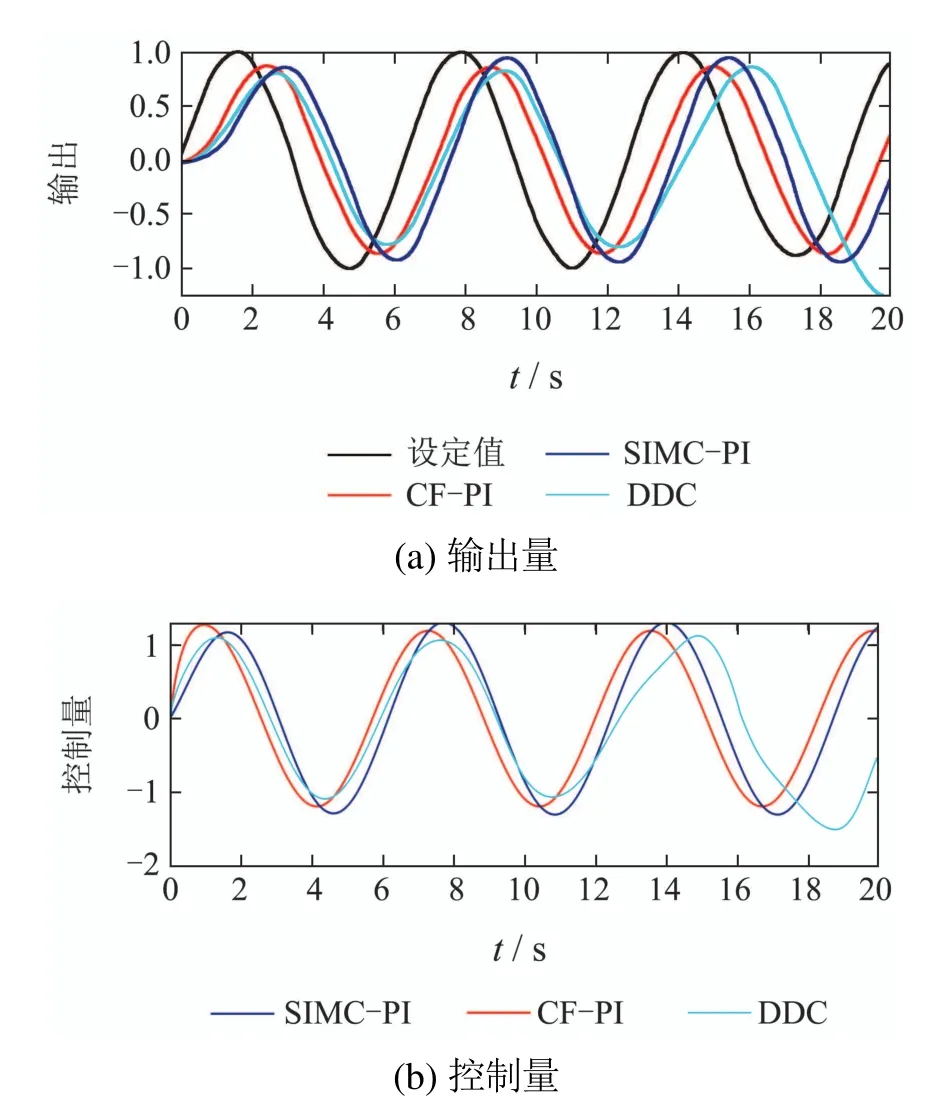
图11 不同控制器作用时正弦响应下的仿真结果Fig.11 The simulation result of sinusoidal response with different controller

上肢肌肉模型具有非常大的不确定性,因此系统不确定性对于控制效果的影响不能忽略.蒙特卡洛实验的核心是“不确定性随机化”,通过将被控对象的参数在一定范围内摄动,可以验证控制器对不确定性系统的控制效果.因此,将式(3)所示模型中的系数在原来值的±20%范围内摄动,重复图10所示的仿真400次,并统计每次仿真中的跟踪IAE指标(IAEsp)和抗干扰IAE指标(IAEid),得到图12所示的IAEsp和IAEid的分布图.

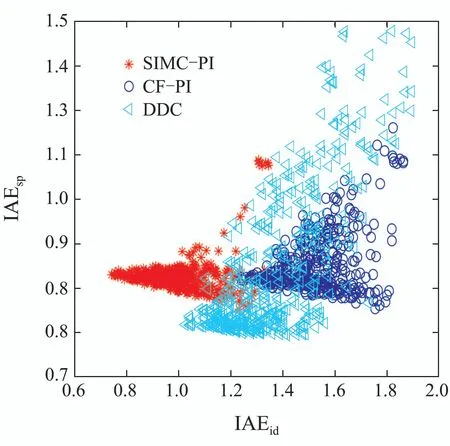
图12 不确定性系统的蒙特卡洛实验结果Fig.12 Monte Carlo experimental results for uncertain systems

IAEsp和IAEid的值越小意味着控制效果越好,IAEsp和IAEid的分布越集中意味着闭环系统的鲁棒性越强.从图中可知CF–PI的IAEsp和IAEid的分布更加集中且具有更小的范围,这说明CF–PI针对不确定性系统时具有更好的控制效果和更强的鲁棒性.尽管DDC有许多比较小的IAEsp和IAEid值,但DDC的IAEsp和IAEid的分布范围最大,意味着DDC随着工况变化时会出现控制性能下降,即鲁棒性较差.由于DDC的鲁棒性较差,在进行实验验证时,只对比CF–PI和SIMC–PI控制策略.

4.2 实验验证

基于上述的理论分析与仿真结果比较,在保持CF–PI和SIMC–PI的参数不变的前提下,分别将CF–PI和SIMC–PI在图1所示的实验平台中验证.

由于康复训练的目的是使病人能够完成生活中常见动作,如取物、开关门等,这类动作可以用周期性信号进行描述.而阶跃信号能够激活系统的大部分模态,阶跃响应可以较好地表征系统的动态特性.因此,本文采用周期性正弦信号和阶跃信号作为期望跟踪信号来验证系统的性能.具体的实验方案如下:分别对实验者施加阶跃信号和周期为2πs、幅值为1的正弦信号,其中阶跃信号在0.3 s时进行变化,每次实验持续7 s;每次正弦信号的实验持续8 s.招募的实验者为实验室人员,在自愿和身体条件允许的基础上展开实验.每一位实验者的等长招募曲线参数在实验前进行辨识并基于辨识的结果设计f−1(u)进行补偿,而回路中控制器参数在整个实验过程中保持不变.由于每位实验者肱二头肌能够承受的最大电极刺激值不同,故实验者在不同目标输出力下进行阶跃实验,其中最大输出力通过开环试验测试得到.

图13为CF–PI在5位实验者在不同目标输出力下的实验结果.从图中可知CF–PI在不同实验者和不同目标输出力作用下都能够更好地跟踪输出力的设定值,且超调比较小.说明CF–PI在系统存在不确定性时仍可以保证比较理想的控制效果,具有较强的鲁棒性.

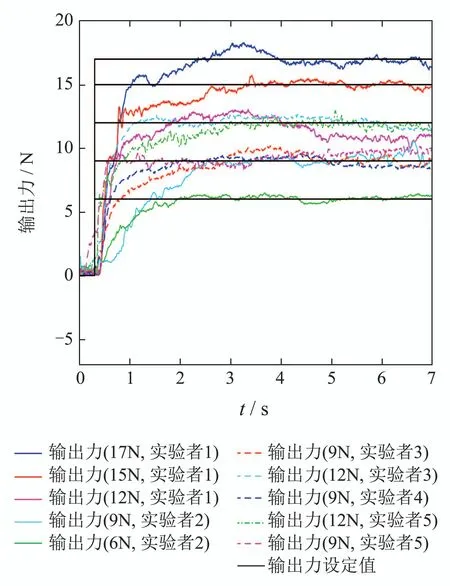
图13 CF–PI作用下的实验结果Fig.13 Experimental results of CF–PI

为防止实验过程中的超调对实验者的肌肉产生不必要的损伤,在进行SIMC–PI控制效果实验时,仅对5位实验者各进行了一次不同设定值下的阶跃实验,实验结果如图14所示.从图可知,SIMC–PI的跟踪性能较CF–PI有比较大的下降,且在输出力为17 N时超调很大.其次,实验者1,3,4和5的SIMC–PI与CF–PI的响应速度比较接近,而实验者2的SIMC–PI跟踪速度较快.由于实验者在实验过程中肌肉反应会由于情绪波动等原因造成肌肉响应特性变化,造成实验者2的SIMC–PI响应速度快于CF–PI.

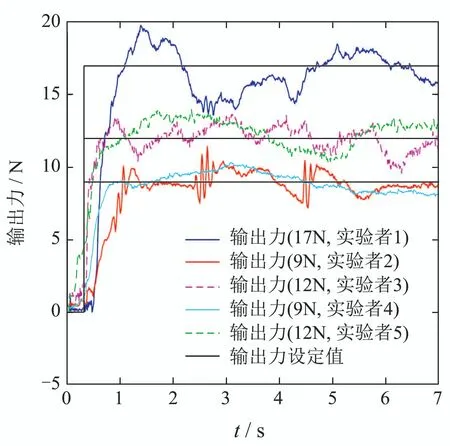
图14 SIMC–PI作用下的实验结果Fig.14 Experimental results of SIMC–PI

此外,尽管控制器参数是根据实验者一的肌肉模型设定的,但从图13和14可以看出,CF–PI和SIMC–PI对不同实验者都具有较强的鲁棒性,表明控制器能够比较好的应对模型的不确定性.最后,从图13可知,同一个实验者对不同目标输出力的跟踪响应速度比较接近,说明输出力的响应与实验者的肌肉特性相关,与阶跃幅值相关性较弱.

为了定量比较控制效果,本文采用上升时间(定义为响应曲线从稳态值10%上升到新稳态值90%所需的时间)、峰值量占比(实验过程中出现的峰值与稳态值的差值占稳态值的百分比)、以及单位IAE指标(IAE指标与阶跃幅值的比值)进行定量比较,相关统计结果如表1所示.由表1可知尽管SIMC–PI具有较快的上升时间,但是平均峰值量占比达17.80%,而CF–PI的平均峰值量占比仅为9.22%.此外,CF–PI的平均单位IAE仅是SIMC–PI的70.43%.因此,与SIMC–PI相比,CF–PI具有更好的输出力跟踪精度和平稳性.

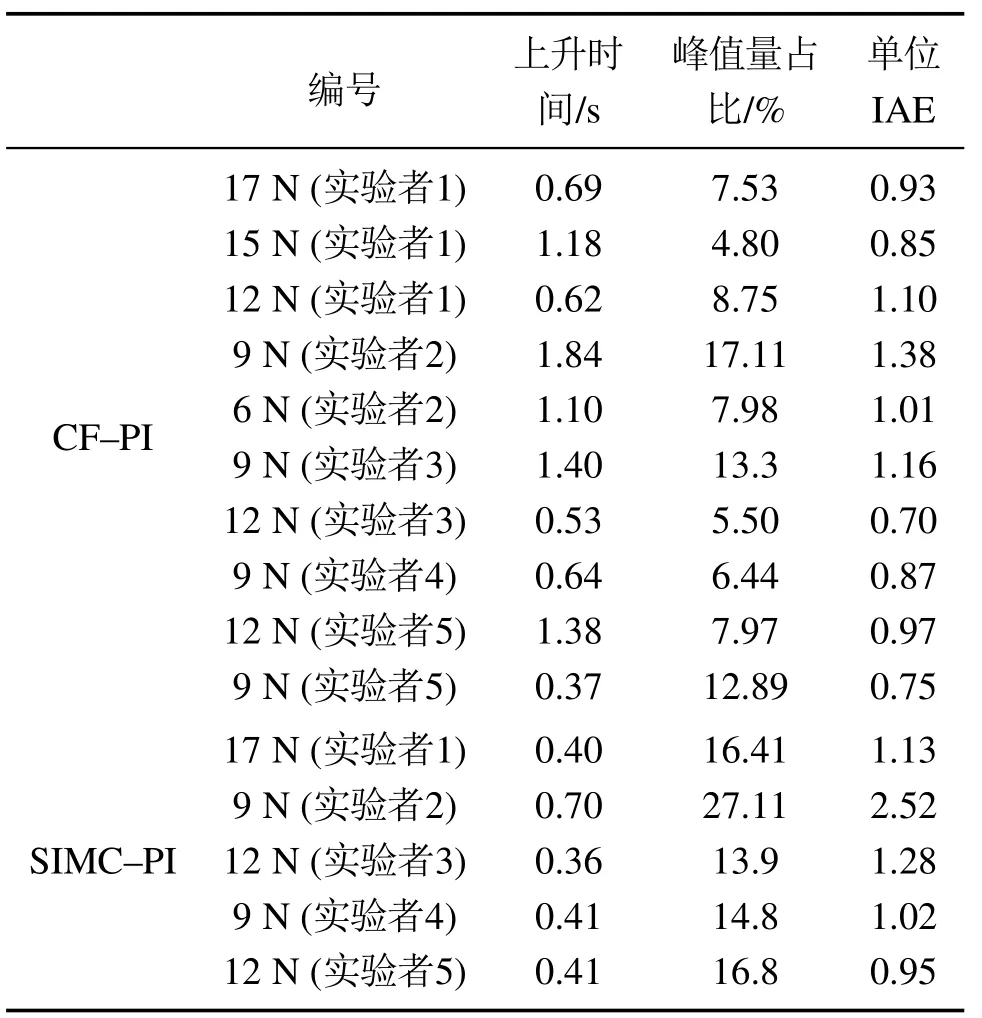
表1 实验结果的统计指标Table 1 The statistical indexes of experimental results

在对正弦期望输出力的跟踪方面,从图15所示两种控制器作用时下实验者3对频率为0.65 HZ的跟踪响应曲线可以看出,二者的IAE指标分别为11.42和23.19,但CF–PI具有更好好的正弦输出力跟踪性能,而SIMC–PI在跟踪过程中响应较慢,且存在一定的相位差.

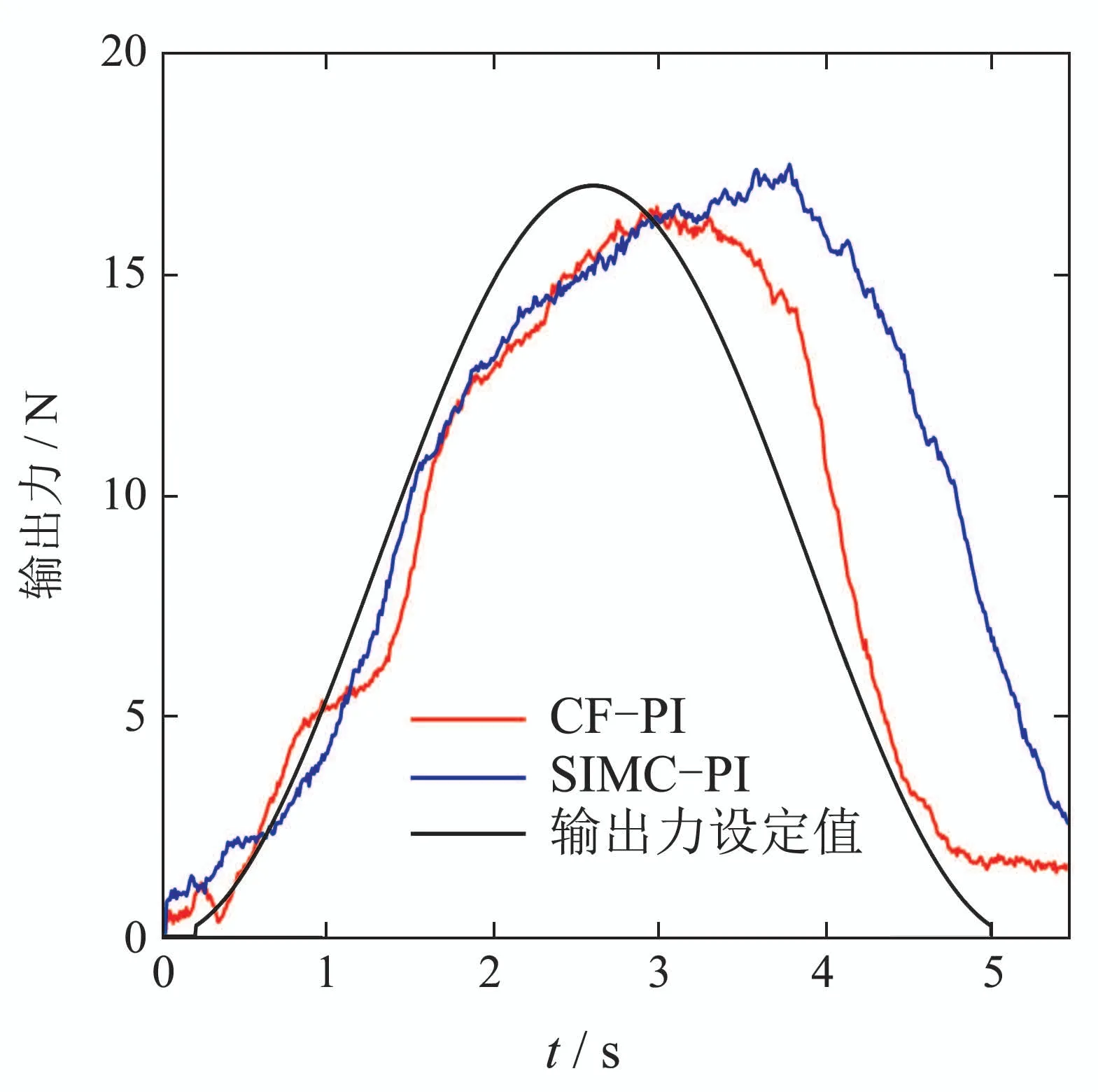
图15 不同控制器时实验者3正弦响应实验结果Fig.15 Experimental results of sinusoidal responses for 3#experimenters with different controllers

综上所述,实验对比结果表明CF–PI方法在保证鲁棒性的条件下对阶跃和正弦目标输出力均具有更好的跟踪性能,展示了其良好的应用潜力.

5 结论

本文关注基于FES技术的闭环控制问题,由于上肢肌肉动态模型存在着强非线性、多源扰动、模型不精确和参数变化大等控制难点,使得设计的控制策略要具有不依赖精确数学模型和强鲁棒性等特点.为提高基于FES的上肢康复系统跟踪速度和扰动抑制的能力,本文提出了一种基于条件反馈的比例–积分控制策略,通过条件反馈设计提高系统的跟踪性能,通过比例–积分控制器抑制扰动与模型的不确定性.然后,采用单一变量法分析了控制器参数对控制效果的影响,提出了一种简单、实用的参数整定规则,仿真结果验证了所提方法在保证更强鲁棒性的前提下,比常规的比例–积分控制器在跟踪和扰动抑制性能具有优势.最后,基于搭建的上肢康复系统控制平台,对不同实验者在不同目标输出力下进行对比实验,实验数据表明本文所提基于条件反馈的比例–积分控制控制策略的平均峰值量占比为9.22%,而对比控制策略的平均峰值量占比为17.80%,所提控制策略的平均单位误差绝对值积分指标是对比控制策略平均单位误差绝对值积分指标的70.43%,所提控制策略在保证闭环系统鲁棒性的前提下具有更好的跟踪性能.