单因素方差分析在煤样均匀性检验中的应用

倪 峰

(1.陕西省能源质量监督检验所; 2.西安科技大学; 陕西 西安 710054)

1 概 述

方差分析( Analysis of Variance, 简称ANOVA), 又称为“变异数分析”, 是英国著名的统计学家罗纳德·费舍尔发明的一种用于检验2 个及2 个以上样本均值差异显著性的统计方法。常见的方差分析类型有单因素方差分析和多因素方差分析。

在GB/T 22279-2008 《煤炭成分分析和物理特性测量 标准物质研制导则》 和CNAS-GL003:2018 《能力验证样品均匀性和稳定性评价指南》等标准中, 标准煤样、 能力验证样品在研制中的均匀性检验就用到了单因素方差分析。

2 单因素方差分析

方差分析是对多个样本均值进行比较的一种统计方法。 谈到均值的比较, 首先会想到t 检验, 这是一种适合小样本数据的统计分析方法,通过比较不同数据的均值, 研究两组数据之间是否存在差异。 如果有多个样本, 可以在两两之间进行t 检验, 但使用这种方法却有很大的弊端;第一, 进行t 检验的组合较多, 计算量大; 第二, 进行t 检验的次数越多, 犯统计学中“第一类错误” 的概率就会叠加, 降低了分析结果的可靠性; 第三, 多次的t 检验, 仅得到一些零散的信息, 缺乏综合的评价。 方差分析则可以对多组试验数据同时进行分析, 将总变异分解为组间变异和组内变异, 并通过组间变异和组内变异的比率来确定影响结果的因素。

为了研究各影响因素, 将同一个煤样进行混合缩分, 分装成多个包装单元, 对每个包装单元样品分别进行多次检测。 能够影响检测结果的原因有很多, 例如不同的检测方法、 缩分后包装单元之间的差异、 使用不同设备检测、 不同的实验人员进行操作等; 这些影响称为因素或因子, 如图1 所示。

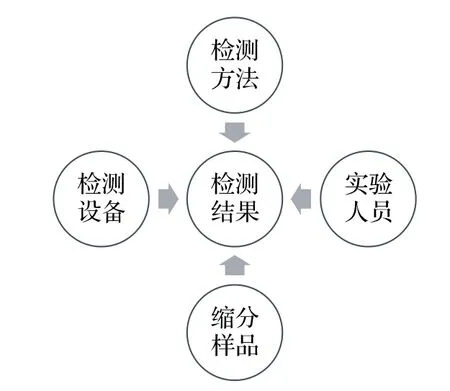
图1 煤样检测结果影响因素

由于各种因素的影响, 检测结果会呈现差异。 造成差异的这些因素通常可分成两类: 一类是不可控的随机因素, 例如方法的精密度; 另一类是可控因素, 例如检测设备、 实验人员、 缩分样品等。 另外, 同一个因素也会有不同的状态,比如不同的检测设备、 不同的检测人员等, 将因素所处的状态称为水平。 如果只研究一个可控的因素在不同水平下对结果的影响, 这就是单因素方差分析。

因此, 在GB/T 22279-2008 《煤炭成分分析和物理特性测量 标准物质研制导则》 中4.3.3规定“均匀性检验应在重复性条件下(同一操作者, 同一台仪器, 同一测量方法, 于短期内)完成”, 即只研究一个可控因素(缩分样品)在不同水平下(不同包装单元)对检测结果的影响。

3 实例解析

将1 份煤样充分混合, 并缩分成4 份质量相等的样品, 每份样品分别在重复性条件下进行3次测定。 对检测数据进行分析, 使用单因素方差分析, 检验样品因素对检测结果是否造成影响。

方差分析研究的对象为“样品” 这个固定因素; 因素的4 个水平分别为1 号、 2 号、 3 号、 4号样品; 随因素变化的结果为因变量, 即检测结果。 样品方差分析因素如图2 所示。

图2 方差分析因素

4 个不同样品(总体), 在相同的实验条件下分别进行了3 次重复测定(样本), 并统计检测结果, 如图3 所示。 同时, 使用柱状图来分组表示

图3 样本抽样

不同样品的检测结果量值情况, 如图4 所示。

图4 检测结果的差异

根据分析可知, 影响检测结果因素包括: 第一类不可控的随机因素, 即检测方法的精密度;第二类为可控的因素, 即样品之间的差异。 将同一个样品内的检测结果差异称为“组内差异”,这主要由随机误差造成的; 将不同样品之间的差异, 称为“组间差异”, 由样品差异和随机误差共同造成的。 可使用方差分析来判断4 组样本均值的差异是由于因素的不同水平造成的, 还是纯粹由于随机因素造成的。

首先, 对检测结果进行误差分析, 任何一个i(i=1、 2、 3……m)号样品的第j(j=1、 2、 3……n)次检测结果可表达为公式(1)。

式中: xi,j为任意一次检测结果; μi为某个样品检测结果的平均值; μ 为检测结果的总平均值; ai=μi-μ 为某个样品的平均结果与总体平均结果之差; εij为随机影响因素。

其次, 分析不同误差造成的差异; 使用离差平方和分别表示总变异、 组间变异和组内变异。

(1)总体数据的离差平方和SST, 即所有检测结果的差异之和为公式(2):

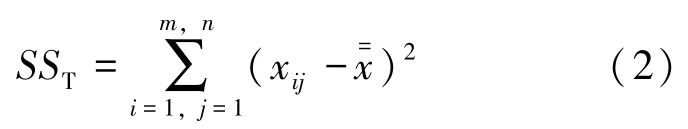
式中: xij为任意一次检测结果;为检测结果的总平均值。

(2)组间离差平方和SSA, 表示组间的差异程度, 由因素水平和随机因素共同导致的差异为公式(3):

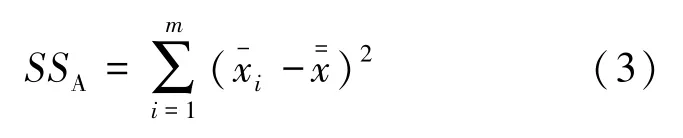
(3)组内离差平方和SSE, 表示组内的差异程度, 由随机因素造成的差异为公式(4):

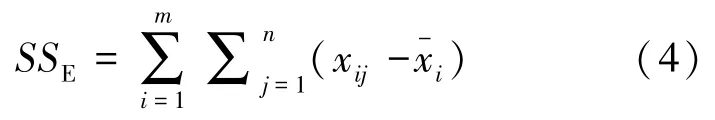
(4)为了消除样本个数对离差平方和的影响,用离差平方和除以相应的自由度。

组间离差平方和SSA和转变为组间方差MSA,受到因素与随机误差的共同影响, 见公式(5):

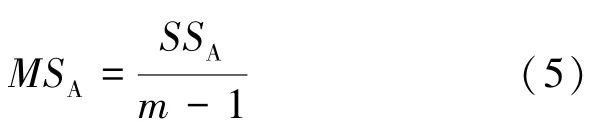
式中: m-1 为组间方差的自由度。

组内离差平方和SSE转变为组内方差MSE,只受到随机误差的影响, 见公式(6):

式中: N 为样本总数, 即m×n; N-m 为组内方差的自由度。

最后, 用一个统计量来检验因素对结果的显著影响, 使用F 分布进行检验, 并对结果进行分析, 见公式(7)。

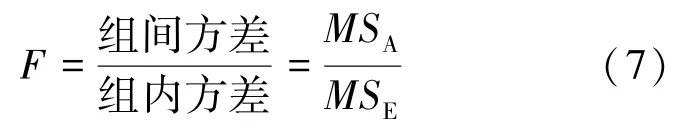
(1)如果样品间差异对检测结果影响不大,那么组内和组间只有随机误差影响, 比值会接近于1。

(2)如果样品间差异对检测结果影响大, 那么组间方差就会大于组内方差, 比值会大于1。

(3)当这个比值大于到某种程度时(F 检验临界值), 就说明不同因素水平存在明显差异, 或者说因素对结果造成显著影响; 不同样品之间的差异过大, 样品不均匀。

4 样品均匀性检验中的应用

在标准煤样、 能力验证样品研制生产中, 将煤样混合均匀后分装到多个最小包装单元内, 并按一定的规则抽取一定数量的样品进行均匀性检验。 例如, 分装了100 瓶煤样, 随机抽取了10瓶样品, 在重复性条件下(同一操作者, 同一台仪器, 同一测量方法, 于短期内)完成, 每瓶样品进行2 次重复测定。 同时, 为了避免测量系统在不同时间段的变差干扰, 测量次序随机进行排列。 选择不易均匀的和有代表性的特性量检测项目煤的灰分进行测定, 检测数据见表1。

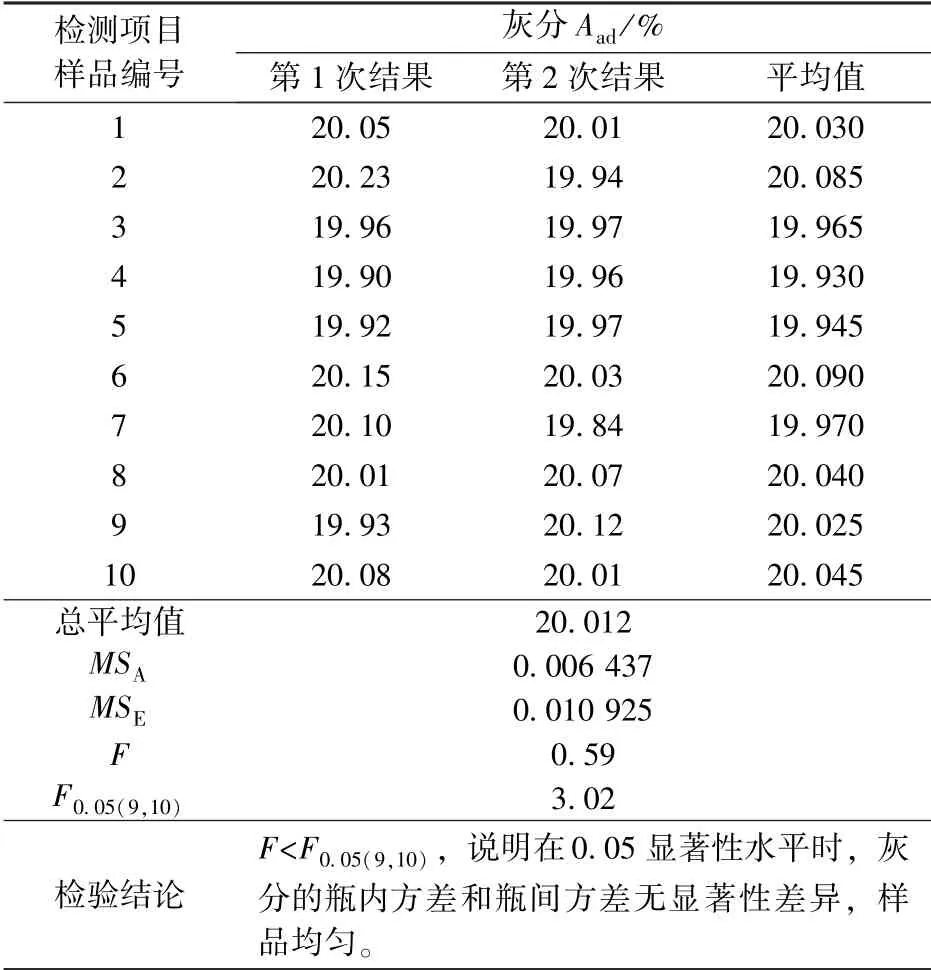
表1 均匀性检测数据

根据上述分析, 对每个最小包装单元样品进行2 次检测, 瓶内检测结果之间的差异即“组内差异”; 瓶与瓶之间差异为固定的因素, 即“组间差异”。 采用单因素方差分析, 检验瓶间的差异是否对检测结果有显著性影响。

从表1 检验结论中可看出, 瓶与瓶之间差异对结果的影响并不大, 组内组间只有随机误差影响, 因此样品是均匀的。

5 结 语

单因素方差分析是一种能使多组间均值检验变得简洁的一种检验方式, 它能同时考虑所有的样本, 不仅能使检验过程变得简洁, 而且能排除因t 检验可能造成错误累积的概率。 因此, 它在样品的均匀性检验中有着广泛的应用。