一种基于3D SVPWM调制的三相四桥臂逆变器控制方法

张 波

(西安特锐德领充新能源科技有限公司，西安 710000)

0 引 言

三相逆变器带不平衡负载时各相输出电压幅值大小有很大差异，且畸变严重[1]。传统的三相三桥臂拓扑由于没有中线，只能带三相平衡负载，无法带单相负载。

传统处理方法是采用分裂电容拓扑，在母线中点引出中线，文献[2]提到此方式可以解耦三相电压控制，但带来的问题是母线利用率降低，母线电容容量增大为原来的2倍，成本增加，更大的问题是在输出限流期间，电流回灌正、负母线，容易造成母线过压故障，导致可靠性不高。

三相四桥臂很好解决了这个问题，与传统分三桥臂拓扑相比，其母线利用率不变，母线电容不变，限流期间母线上能量有进有出，无母线过压问题，而且可以带单相负载。但由于引入了第四桥臂，传统的两电平SVPWM难以满足要求，用SPWM也无法解耦四桥臂模型，有文献[3-4]提出将第四桥臂独立控制，但因为与其他三桥臂不是一个整体，控制变得不解耦，控制效果变差。本文提出了一种将四桥臂作为一个整体的逆变器控制方法，利用正负零序分量解耦控制，此方法对三相负载的不平衡度有很强的抑制作用，同时简化了3DSVPWM发波，在工程容易实现。

1 三相四桥臂逆变器模型

三相四桥臂逆变拓扑结构如图1所示。图中Vn,Va,Vb,Vc分别为四相发波电位，in,ia,ib,ic分别为四相电感电流，VoA,VoB,VoC分别为三相输出对N点的电压，ioA,ioB,ioC为三相负载电流，icA,icB,icC为三相输出电容电流，N点为负载中点，Udc为母线电压。

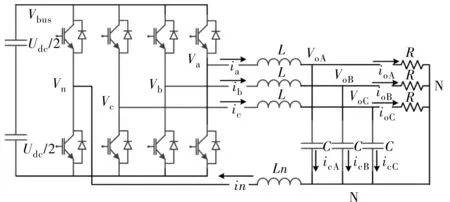
图1 三相四桥臂逆变拓扑

假定ABC三相电流方向流出桥臂为正，N相电流流入桥臂为正，电容电流流入N点为正，在ABC坐标系下得到：

(1)

式中，r为电感内阻，L为ABC三相电感，Ln为N相电感。

四桥臂拓扑中有16种开关状态，对应16种开关矢量，各个桥臂的开关状态用开关符号Sx表示，如下：

(2)

因此臂间电压Vxn=(Sx-Sn)Udc,x=a,b,c

根据状态空间平均理论，状态开关Sx等效为占空比D，因此通过控制四个桥臂的开关管占空比，就可以控制臂间电压，根据式(1)可知也就可以独立的控制三相输出电压VoA,VoB,VoC。

但是有一个问题是VNn无法直接计算出来，也就是在abc坐标系下，会有一个VNn估算不准确，影响三相的解耦，进而影响控制精确度。

利用Clark变换，可消除VNn的影响，将abc坐标系转换到αβγ坐标系，由式(1)得：

(3)

假设Ln=L，因为γ轴与αβ轴垂直，所以是解耦的，因此利用Park变换将αβ坐标系转换到dq坐标系，在加上原有的γ轴，就形成了新的dqγ模型如式(4)，此模型中的各变量都是直流量，且在三维空间上相互正交，从而使得臂间电压Vxn的控制更为精确。

(4)

式中,Vd,Vq,Vγ是臂间电压对应的旋转矢量，id,iq,iγ是三相电流的旋转矢量，Vod,Voq,Voγ是三相输出电压的旋转矢量。根据式(4)得到系统模型如图2所示。由图2分析可知，三相四桥臂经过旋转变换后，模型完全解耦，dqγ三轴可独立控制。

图2 三相四桥臂逆变dqγ坐标系模型

2 3DSVPWM简化调制方法

在模型确定后，如何发出臂间电压成为关键，3DSVPWM发波方式的提出可以解决这个关键问题，文献[5]提出了一种3DSVPWM的简化方法，但没有具体说明推导过程。

将四桥臂逆变器的16个开关状态与三相臂间电压Vxn对应起来得到表1。

表1 四桥臂开关状态表

再将表1的16个状态由abc坐标系转换至αβγ坐标系，可以得到αβγ坐标系下的开关矢量。根据各矢量在αβγ坐标系下的投影，在三维坐标系中描绘出图3。

由图3可见，将三维空间分成6个三棱柱，每个三棱柱里有6个非零矢量，可以将三棱柱分成4个四面体，也就是整个三维空间有24个空间四面体,需要对每个四面体的组成矢量逐个分析。

图3 三维空间矢量图

有文献根据abc坐标系标量的符号去判断矢量所在的四面体，一是没有提及理论依据，二是在计算空间矢量时标量坐标系与矢量坐标系来回切换，计算量大，浪费芯片资源，在工程不易实现。

如果将其投影到αβ平面上，则与普通的二维空间矢量图一致，只是多了第四桥臂的开关状态，如图4所示。

图4 二维空间投影图

因此提出一种简化的3DSVPWM计算方法，此方式全部在αβγ坐标系下计算得出所有矢量以及分区，下面描述计算依据与实现步骤。

(1)步骤1

按照三维矢量的平面投影分成6个主扇区，对应6个三棱柱，将6个三棱柱顺时针全部旋转到第一扇区的三棱柱，可以发现，第135扇区的三棱柱为同一构造，第246扇区的三棱柱为同一构造。以第1、2三棱柱为例如图5所示，每个三棱柱根据面ΔAOB、ΔBOC、ΔCOD、ΔDOC又可以分为4个子扇区。以下计算均根据图5展开。

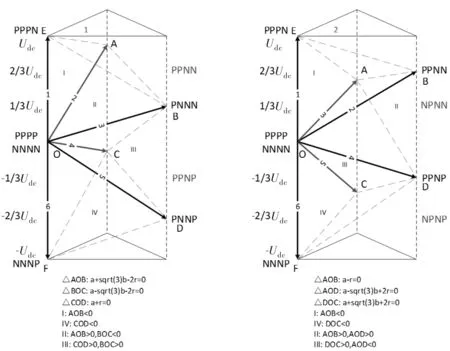
图5 第1、2主扇区三棱柱矢量图

(2)步骤2

将三棱柱的αβ平面投影(图4)，与传统的二维SVPWM一致，根据六边形的对角线方程，先判断6个主扇区，流程图如图6所示。

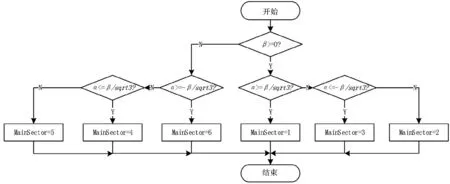
图6 主扇区判断流程图

(3)步骤3

根据图5，第1主扇区三棱柱被ΔAOB、ΔBOC、ΔCOD三个面分成4个四面体，参考αβγ三维坐标系的平面方程如下。

ΔAOB：α-γ=0

本步骤流程图如图7所示。

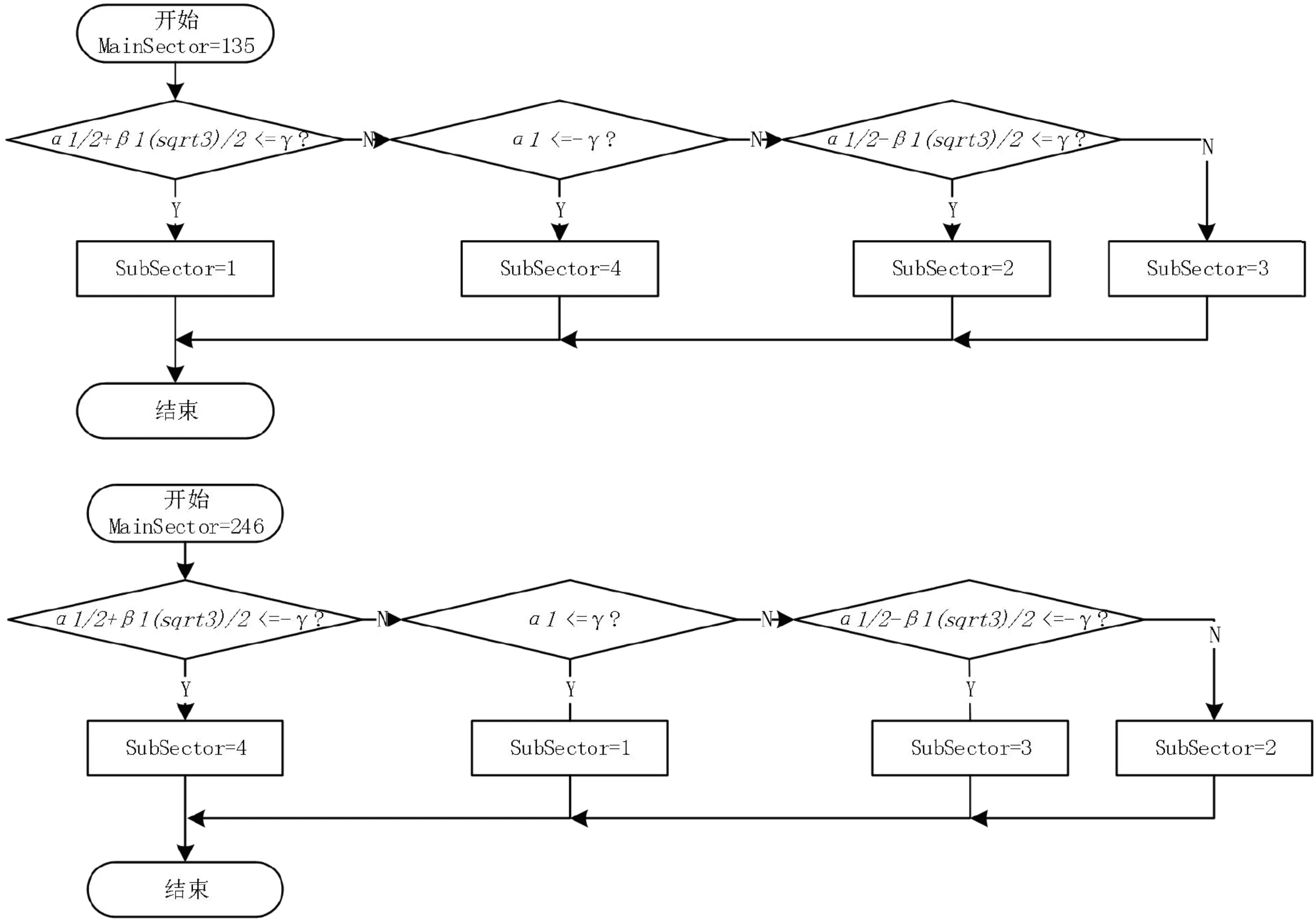
图7 子扇区判断流程图

(4)步骤4

(5)

(5)步骤5

如图5，在三维坐标系下，每个矢量由子扇区中的三个非零矢量组成，分别在不同的四面体子扇区按照式(6)计算各自矢量作用的时间t1,t2,t3。

(6)

式中，Urefα,Urefα,Urefγ是发波矢量的αβγ轴分量，U1α,U1β,U1γ是子扇区1号矢量的αβγ轴分量，U2α,U2β,U2γ是子扇区2号矢量的αβγ轴分量，U3α,U3β,U3γ是子扇区3号矢量的αβγ轴分量，t1,t2,t3是子扇区1、2、3号矢量一个周期Ts内对应的作用时间。

(6)步骤6

(7)

根据图5将每个扇区都按照以上方法计算一遍，得到所有扇区的矢量作用时间，如表2所示。

表2 αβγ坐标系下的四桥臂开关矢量时间表

(7)步骤7

根据各个扇区矢量的作用时间，按照谐波最小原则，构造发波时序，以第1主扇区第1子扇区为例，如图8所示。

图8 3DSVPWM发波时序

以上方法将6个三棱柱旋转到第1个三棱柱，将三棱柱构造归一到两种，原来分别要计算24个四面体，现在只需要计算8个，并且利用了传统二维SVPWM的结论，只需要简单的加减运算就可以计算出3DSVPWM的各个矢量时间，在判断子扇区时，只利用了αβγ分量，不需要反变换到abc坐标系，节省了计算开销。

3 四桥臂逆变器不平衡负载控制方法

根据图1拓扑，因为第四桥臂的存在，控制负载N线的电流成为了可能，所以较传统的三桥臂拓扑，最大的优势在于可以带缺相负载，如果控制不解耦，在带单相或者两相负载时，空载的相电压就会受到影响。因此在带缺相负载时，三相电压的不平衡度控制是关键。

根据对称分量法，三相不平衡的量都可以分成三组各自对称的量，分别是正序、负序、零序。基于此，如果将这3种分量都可以做到无差控制，那么三相不平衡问题也就可以解决。

传统的矢量控制无法控制零序分量，所以无法实现缺相运行。四桥臂拓扑，3DSVPWM发波中引入了γ轴，使得控制零序分量成为可能。

由第1节的图2的dqγ模型分析可知，将abc坐标系变换到旋转坐标系dqγ上是解耦的。γ轴体现了零序分量的特征，dq轴上含有正负序分量的特征。

根据dq变换理论可知，如图9，矢量E逆时针旋转得到正序坐标系矢量eP，其中的负序分量在正序dq坐标系下表现为2倍基波频率的交流量，矢量E顺时针旋转得到负序坐标系矢量eN，其中的正序分量在负序dq坐标系下表现为2倍基波频率的交流量。

图9 正负序分量旋转矢量

利用双同步坐标分离法先分离正负dq分量，根据图2的dqγ模型，对正负零序分量分别控制就可以实现各种不平衡载的控制，图10给出了该方案的控制框图。

图10中，ωp是正坐标系角频率，ωn是逆坐标系角频率，与正坐标系符号相反，该控制框图包括三部分。

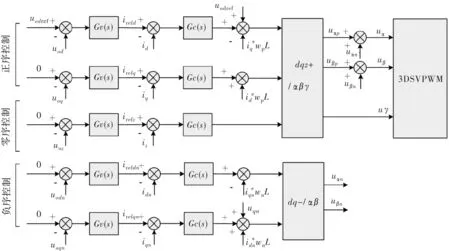
图10 逆变器正负零序分量控制框图

第一部分是正序控制，在正序坐标系下，以d轴电压定向，逆变器控制目标只有正序的d轴分量，q轴给定为0，经过正序的电压电流控制，得出正序发波量经过dqγ+/αβγ(正序帕克变换)得到uαp,uβp。

第二部分是负序控制，在负序坐标系下，dq轴目标均为0，经过负序的电压电流控制，得出负序发波量经过dq-/αβ(负序帕克变换)，得到uαn,uβn。

第三部分是零序控制，γ轴与dq平面垂直，没有耦合项，零序电压目标为0，经过零序的电压电流控制后，得出零序发波量uγ。

在静止坐标系中可以将uαp,uαn直接相加得到uα，将uβp,uβn直接相加得到uβ，再经过第三节所述的3DSVPWM发波，就可以解决三相逆变器带不平衡负载问题，即使在极限情况缺相负载下，也可以保证三相电压平衡。

4 仿真分析及实验验证

文献[1]指出三相电压不平衡度是用电压负序、零序基波分量与正序基波分量的方均根值百分比表示。使用Matlab软件仿真验证上述方法的正确性。

三相四桥臂逆变器仿真系统参数为额定功率10 kW，额定电压220 V，滤波电感140 μH，电感等效内阻0.1 Ω，输出电容3.3 μF。不平衡负载验证极端情况，分别针对线性载与非线性载，进行三相满载、缺一相满载、缺两相满载进行仿真验证。仿真结果如下。

(1)线性负载

线性负载时仿真结果如图11～图13所示。

图12 AB相带载仿真波形

图13 A相带载仿真波形

线性负载不平衡度分析如表3所示。

表3 线性负载不平度计算

(2)非线性负载

非线性负载仿真结果如图14～图16所示。

图14 ABC相带载仿真波形

图15 AB相带载仿真波形

图16 A相带载仿真波形

非线性负载不平衡度分析见表4。

表4 非线性负载不平度计算

由表4～表5分析可知，在不平衡负载的极限情况缺相负载下，线性载不平衡度最大0.802%，非线性载不平衡度最大0.434% ，均远小于业界3%不平衡度指标。其原因在于四桥臂拓扑结合3DSVPWM，再对三相电压的正负零序分量分别解耦控制，可以有效的抑制三相不平衡负载，因为任何三相电压都可以分解为正负零序分量，此方式把正负零序分量经旋转变换都转换成直流量控制，因此仅用PI调节就可达到无差效果，简化了控制，提高了控制精度。

由图11～图16可见，在0.6 s瞬投满载时，线性载无跌落，非线性载在3个周期内就可以恢复，因为在三相电压在动态瞬间也可以分解成正负零序分量，此方式对正负零序分量解耦控制，因此对负载动态也有很好控制效果。

为了进一步验证该方法，按照仿真参数搭建10 kW三相逆变器试验系统，图17～图19为带10 kW线性负载时，系统带三相载、两相载、单相载的电压电流波形，图20～图22为带非线性负载时，系统带三相载、两相载、单相载的电压电流波形。

图17 ABC相带线性载实际波形

图18 AB相带线性载实际波形

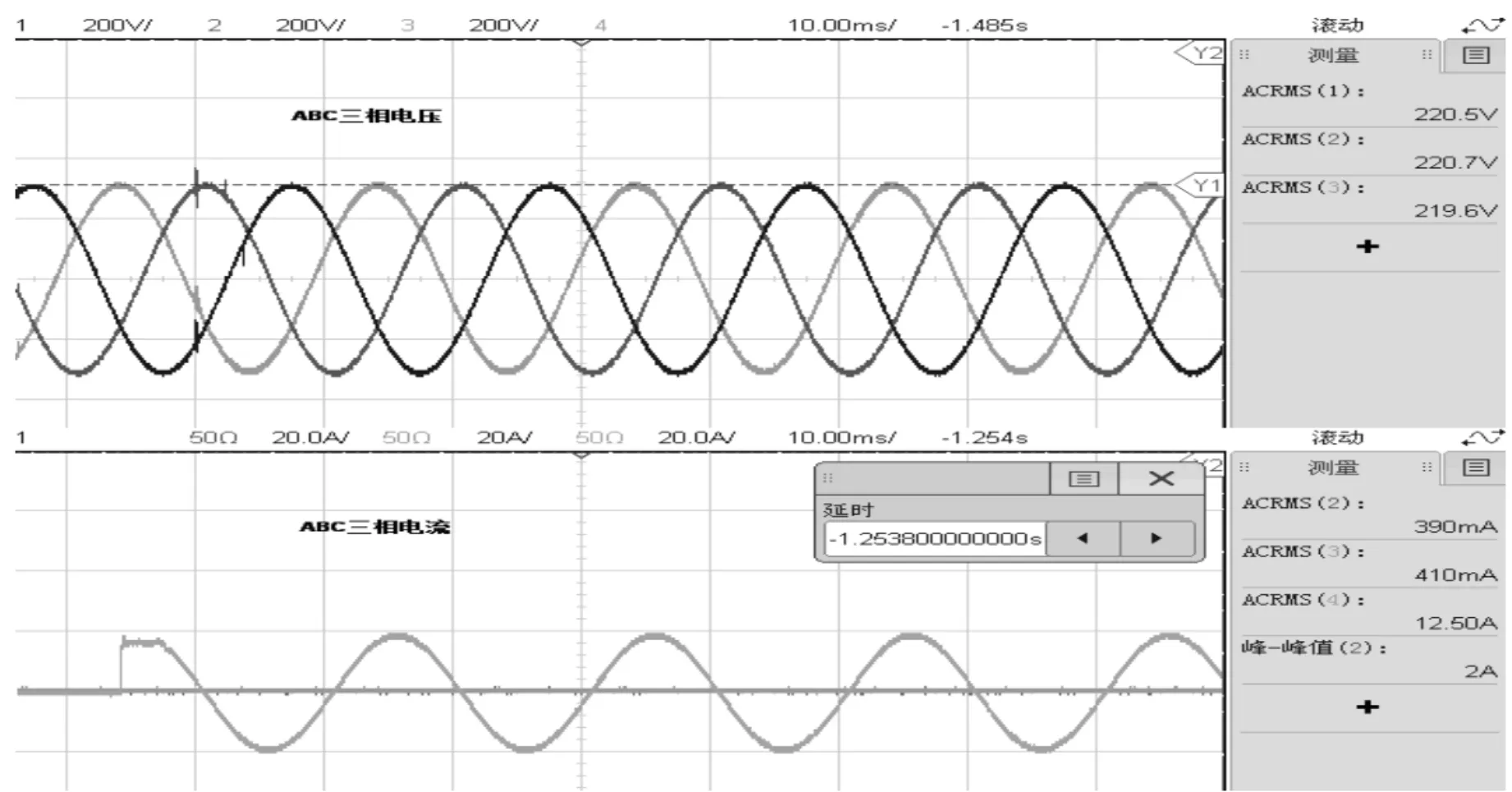
图19 A相带线性载实际波形

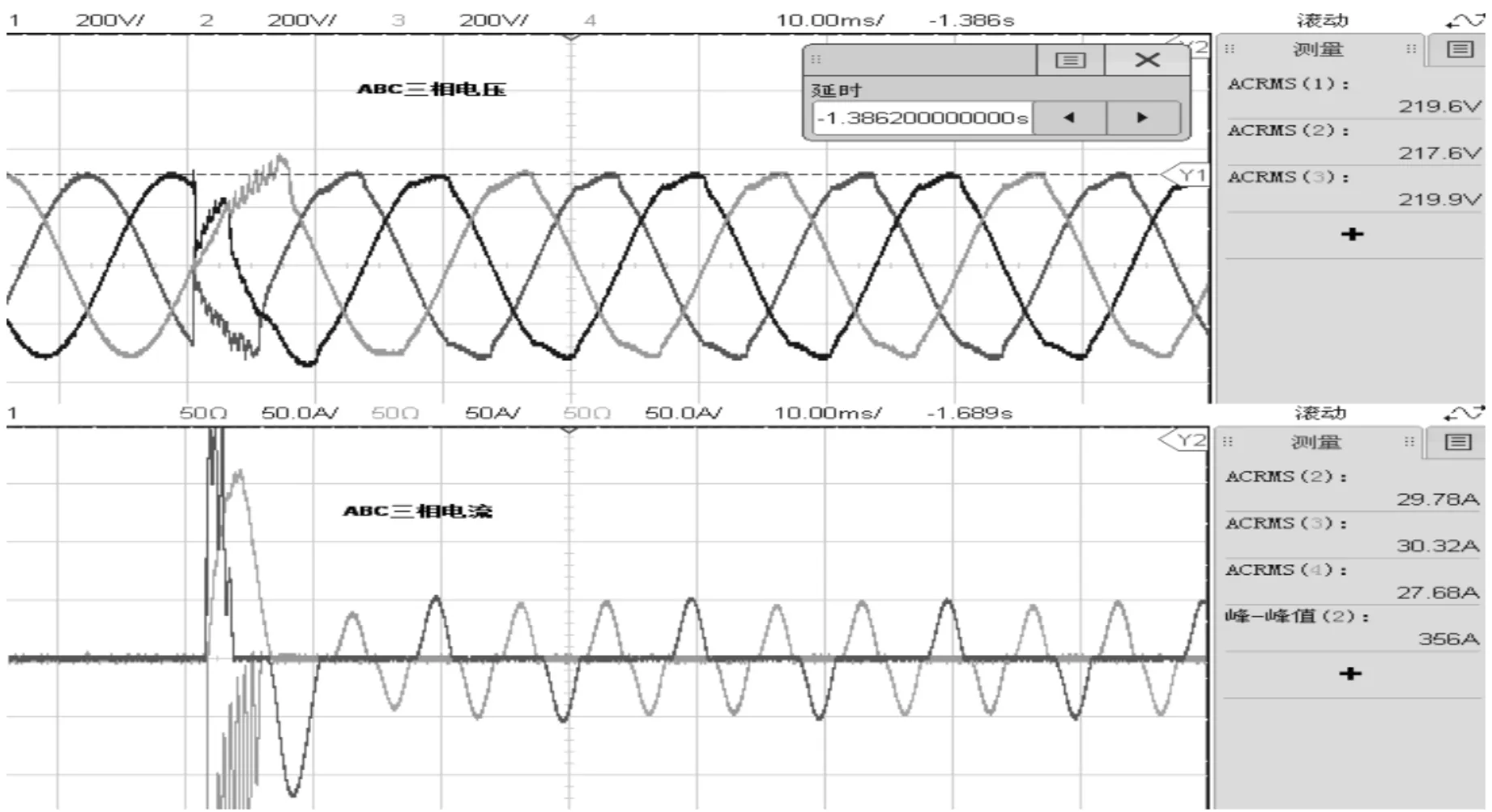
图20 ABC相带非线性载实际波形

图21 AB相带非线性载实际波形

图22 A相带非线性载实际波形

实际波形(图17～图22)，与仿真波形(图11～图16)一致，实验结果证明这种基于3DSVPWM的三相四桥臂逆变器控制方法，无论是线性还是非线性负载，对于不平衡负载的各种工况均有很好调节作用与控制效果，验证了该方法的正确性。

5 结 语

本文针对三相四桥臂逆变器，首先建立了dqγ坐标系下的数学模型，然后利用坐标旋转将原来24个四面体归一成8个四面体，简化了3DSVPWM实现方法，最后根据三相对称理论，对三相逆变器分别进行正序、负序、零序解耦控制。通过仿真与实验，证明了此种方法不论在线性或非线性载下，对缺相这种极端不平衡负载，对其三相电压不平衡度有很好的控制效果。具有一定的理论价值和实际应用价值。