一种集成车载充电器的优化直接功率控制

顾鸿赟，刘陵顺，李 岩 ，闫红广

(1.海军航空大学 航空基础学院，山东 烟台 264001；2. 中国人民解放军92925部队，山西 长治 046000)

0 引 言

伴随世界工业的高速发展，能源危机和环境污染成为了近十几年来人们关注的热点问题。由于新能源汽车使用了低碳减排的电能驱动，因此成为了多国的战略性新兴产业[1-3]。电动汽车发展的问题之一就是电池充电，根据充电方式不同，可分为非车载充电器(Off-board Charger)和车载充电器(On-board Charger)。非车载充电器，即充电器与车体分离，能够提供大功率、品质高的电能，但造价高、体积重量大，多用于大型充电站中；车载型充电器是将充电设备集成在车体内部，虽然体积重量受限、充电功率小，但成本较低，便于携带、充电地点不受限制，使用方便灵活。因此，高性能、大功率的车载充电器成为了未来发展趋势。

目前，多相永磁同步电机在驱动充电集成化拓扑中研究较多，文献[4-6]对不同拓扑结构进行了讨论，其中文献[4]对五相、六相、九相电机驱动充电拓扑结构及无转矩充电模式进行了介绍。文献[7-10]拓扑结构上多采用传统N相电源变换器，当电机相数较多，系统中的电力电子元件数目多。在控制方面，文献[11-13]采用电压外环与电流内环相结合的双闭环PI控制来交直流端电能转换和功率矫正(Power Factor Correction，PFC)，这类方案的动态性能较差，抗扰性较弱。文献[14-15]采用直接功率控制的方法，能让系统在单位功率因数下运行，但谐波污染上需要改进。

本文将三相电源供电的九开关电源变换器(Nine-switch Converter，NSC)和双Y移30°非对称六相电机集成到充电系统的拓扑结构，通过优化直接功率控制方法，在实现充电驱动一体化的同时，减少了电力电子元件的数目，提高了充电模式下的功率因数、改善了电源品质。

1 集成充电器的拓扑结构及工作原理

1.1 电磁转矩为零的充电模式原理

基于九开关变换器的双Y移30°非对称六相电机的三相集成充电器拓扑结构，如图1所示，系统由三相电网、双Y移30°非对称六相电机、九开关变换器组成。当系统工作在充电模式下，接入外部三相交流电，继电器S1～S4打开，九开关变换器的中间开关Gm1～Gm3始终导通(等同于短路)，电源A相连接电机a、d相，B相连接b、f相，C相连接c、e相。本文主要研究集成充电器无扭矩整流过程，有关九开关驱动问题详见文献[16]，DC-DC二级变换器和蓄电池暂不考虑，并用电阻代替。

图1 一体化集成充电器拓扑结构原理图

电机转子是在定子产生的旋转磁场作用下转动的，对于具有两个独立中性点的六相电机，按照图1中的方式与三相电源连接，当电流通过定子绕组时，相当于两套三相定子绕组产生了大小相同但旋转方向相反的对称旋转磁场，磁场同时作用在电机转子上，力矩相互抵消，因而使得电机保持静止。与此同时，电机的定子绕组还可以作为充电滤波电感，不用外加滤波元件，降低了充电器的重量和成本。

根据文献可知，相电流经Clark变换后，电流分量iα、iβ为

(1)

从式可以看出，电流分量iα、iβ的数值大小成比例(iα/iβ≈3.73)，相位相同。因此，电流在机电能量转换平面(α-β子空间)内只产生了脉动的磁场，而没能形成旋转的磁场，所以电机中没有转矩产生。也就是说，在充电模式下，电机转子不需要机械锁定就可以保持静止状态。

1.2 充电模式下拓扑结构图等效简化

通过之前的计算分析，在充电模式下，九开关变换器的中间三个开关处于导通状态，电机转子不旋转，定子绕组充当滤波元件，所以充电模式下的拓扑结构可以等效为图2所示的电路图。由于两两支路并联，每相定子绕组电阻、电感相等，因此图2的电路图可进一步等效为图3所示的电路图，即系统可简化为经典三相电压源整流电路。

图2 拓扑结构简化图

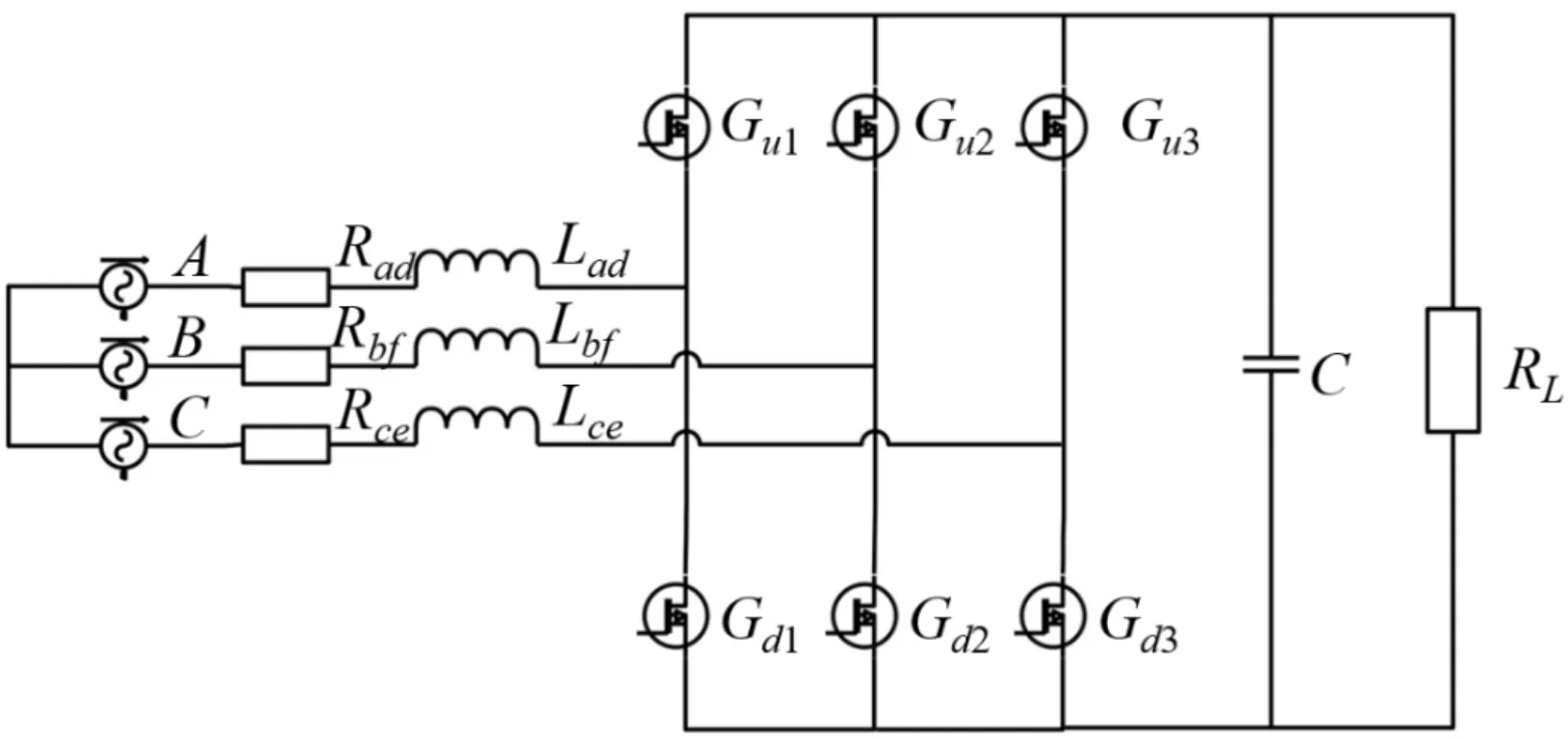
图3 拓扑结构最终简化图

2 基于直接功率控制理论的控制算法

2.1 预测直接功率控制算法设计

预测直接功率控制主要由三部分组成：瞬时功率计算、模型预测计算和有功功率计算。相比于传统直接功率控制，预测直接功率控制减少了对采样频率和传感器精度的依赖，降低了交流侧电感选择的难度。本文改进的预测直接功率控制原理图如图4所示。

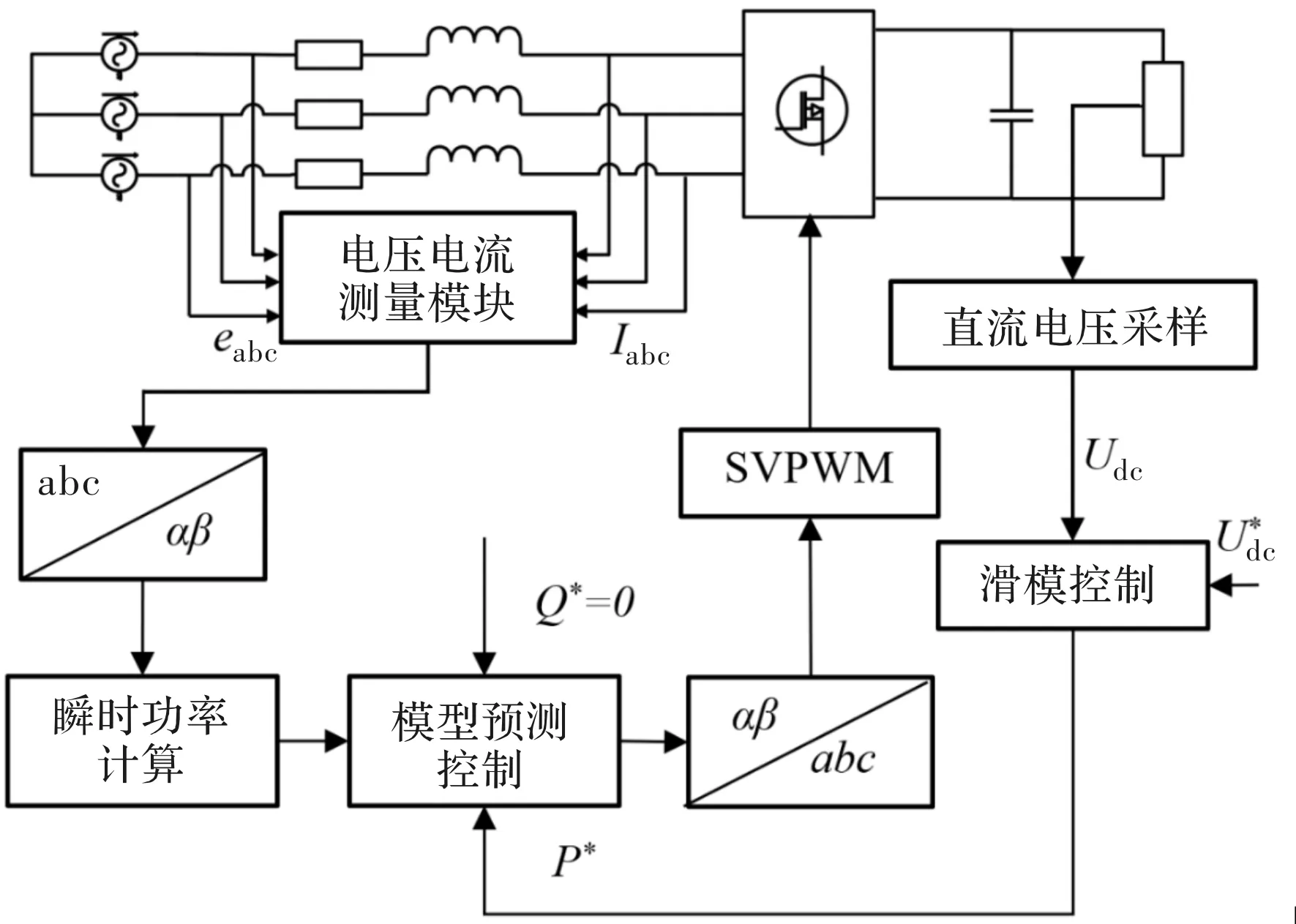
图4 改进的预测直接功率控制原理图

在α-β坐标下，三相整流器的瞬时功率P和瞬时无功功率Q可表示为

(2)

设采样频率远远高于电源电压频率，则可以近似认为在两个相邻周期内离散化电压公式可以写成：

(3)

通过式(2)、式(3)可以推出离散化P、Q变化量：

(4)

根据Kirchhoff laws可以将电压型整流电路的微分方程表示为

(5)

对于式(5)，忽略电阻R的影响，进行离散化，得：

(6)

根据预测控制的思想，控制的最终目的是实际值与期望值一致，因此令：

(7)

将式(2)～式(7)结合，解算得：

(8)

在充电模式控制系统中，充电功率较大，为减少对外部电网得污染，实现系统单位功率因数运行，因此直接设置Q*=0，而对于P*在相邻周期内不可能是完全线性变化的，为了减小模型预测中的误差以及充电过程中干扰的影响，因此采用二阶拉格朗日插值法进行求算[17]。

假设已知P(k)、P(k-1)、P(k-2)，则P*的二次抛物线插值为

(9)

由于采样频率不变，因此求得A0=1，A1=-3，A2=3。即：

P*(k+1)=P(k-2)-3P(k-1)+3P(k)

(10)

将Q*=0及式代入式可得：

(11)

式(11)得到的电压分量，将作为SVPWM模块的控制量。

2.2 基于滑模控制原理的参考功率设计

对于车载充电器的直流侧，希望系统有稳定的电压输出，经典电压外环控制器设计多是采用PI反馈调节，而由于整流过程是一个非线性、时变过程，PI控制器的参数对系统的稳定性影响较大。本文采用自适应滑模控制策略，在系统受到外部干扰和系统参数微变时能够更好的保证系统的稳定性，响应更快，鲁棒性更好。

在每一个周期内，忽略较小的电路损耗，系统的输入(交流测)与输出(直流侧)功率相等：

(12)

式中,Pdc为输出(直流)侧有功功率，Pac为输入(交流)侧有功功率。

设计选取滑模面S为

(13)

式中，k为不等于零的调控参数。对于直流电压参考值Udcref，根据系统需要，一般设为不变常数，则dUdcref/dt=0；并将式(12)代入式(13)，并令滑模面S=0，可得：

(14)

在一个周期内，为了满足滑模条件，使得S=0，并期望系统的有功功率与参考值应相等，即：

(15)

式中，P*为预测直接功率控制中的参考有功功率。

2.3 SVPWM技术实现开关控制

传统的直接功率控制策略(DPC)的实现主要由功率计算模块、功率滞环比较器和开关表组成，系统结构相对复杂，并且采用开关表进行控制，不但开关频率不固定，而且若开关信号选择不恰当会造成功率失调。虽有各类优化开关表的方法来提高开关信号的精准度，但将使开关频率过高、系统结构进一步复杂。

为了提高控制的精准度、固定开关频率，本文采用SVPWM技术实现对开关的控制，将式(8)计算得出的电压矢量Uα、Uβ通过SVPWM技术产生调制信号驱动充电器电力开关，实现对充电器功率的预测控制，获得期望的直流电压输出，并保证系统的在单位功率因数下运行。

3 仿真结果

本文所提出的集成车载充电器控制策略在Matlab/Simulink环境下的仿真结果在本节给出。有关双Y移30°非对称六相电机的仿真模型详见文献[18-19]，系统参数在表1中给出。

表1 系统参数

仿真模型结构图如图5所示。车载充电器的控制模块主要由滑模控制模块、预测直接功率控制模块和SVPWM模块组成。由图5可知，滑模控制计算出的参考有功功率P*、参考无功功率Q*=0交流侧电网电压和电流经过Clark变换所得的αβ分量以及实测的有功功率P无功功率功率Q都作为预测直接直接功率模块的计算参数，经该模块计算后得到电压分量通过SVPWM模块得到功率开关的控制信号，最终实现对功率开关的控制。

图5 系统仿真结构图

按式(11)搭建的预测直接功率模块的仿真图如图6所示。

由图6可知，当系统工作在充电模式下时，电机电流分量iα、iβ同相位,如图7(a)所示，数值上成比例(iα/iβ≈3.73)，验证了电机中定子绕组无法形成旋转磁场。运行中电机的电磁转矩非常小,如图7(b)所示，数量级在10-5Nm，近似为0，如此小的转矩无法克服电机阻尼转矩使得转子转动，因此转子机械角速度为零如图7(c)所示。

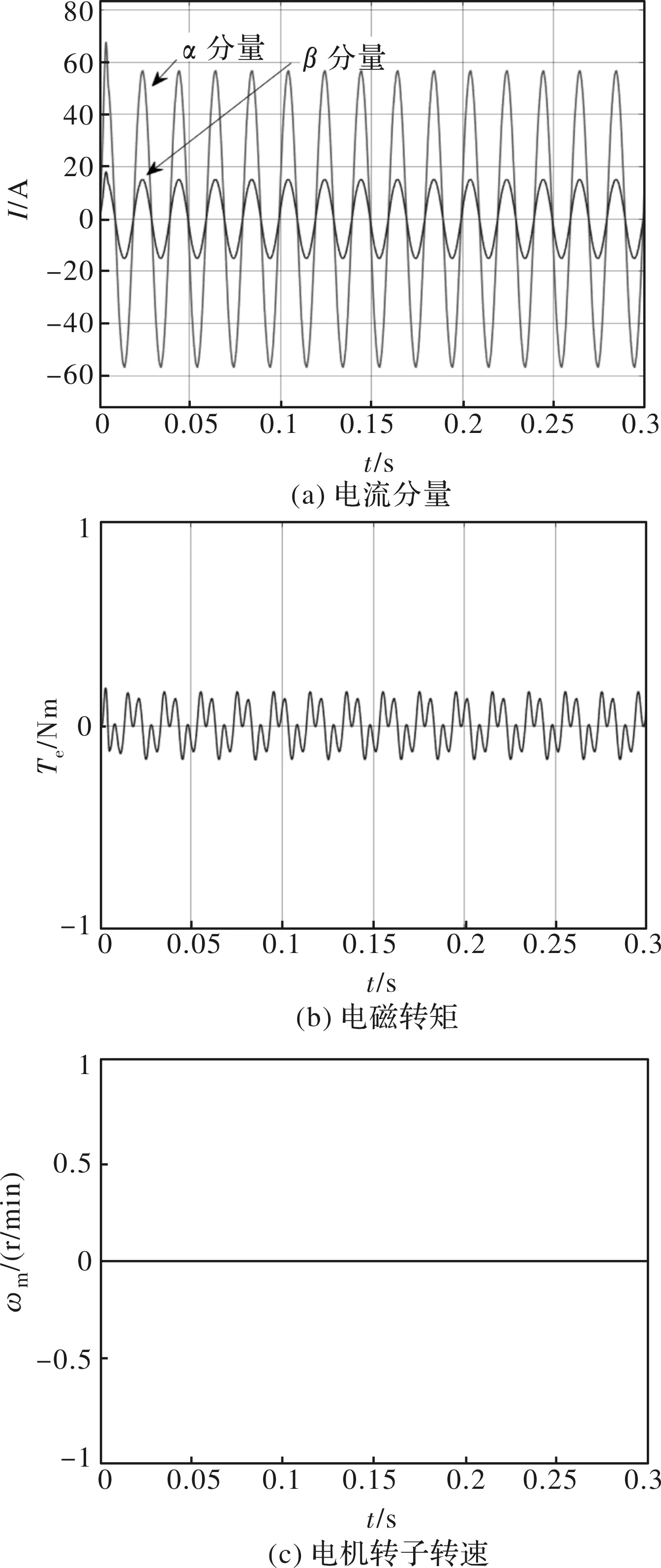
图7 电机运行特性

系统直流侧电压波形如图8所示，可以明显看出，滑模控制算法能使直流侧在0.05 s以内稳定在给定电压800 V，在实际的应用中足够满足要求如图8(a)所示。对于交流侧，三相电源A相电流在稳定后波形十分接近正弦波，有利于减少谐波分量。

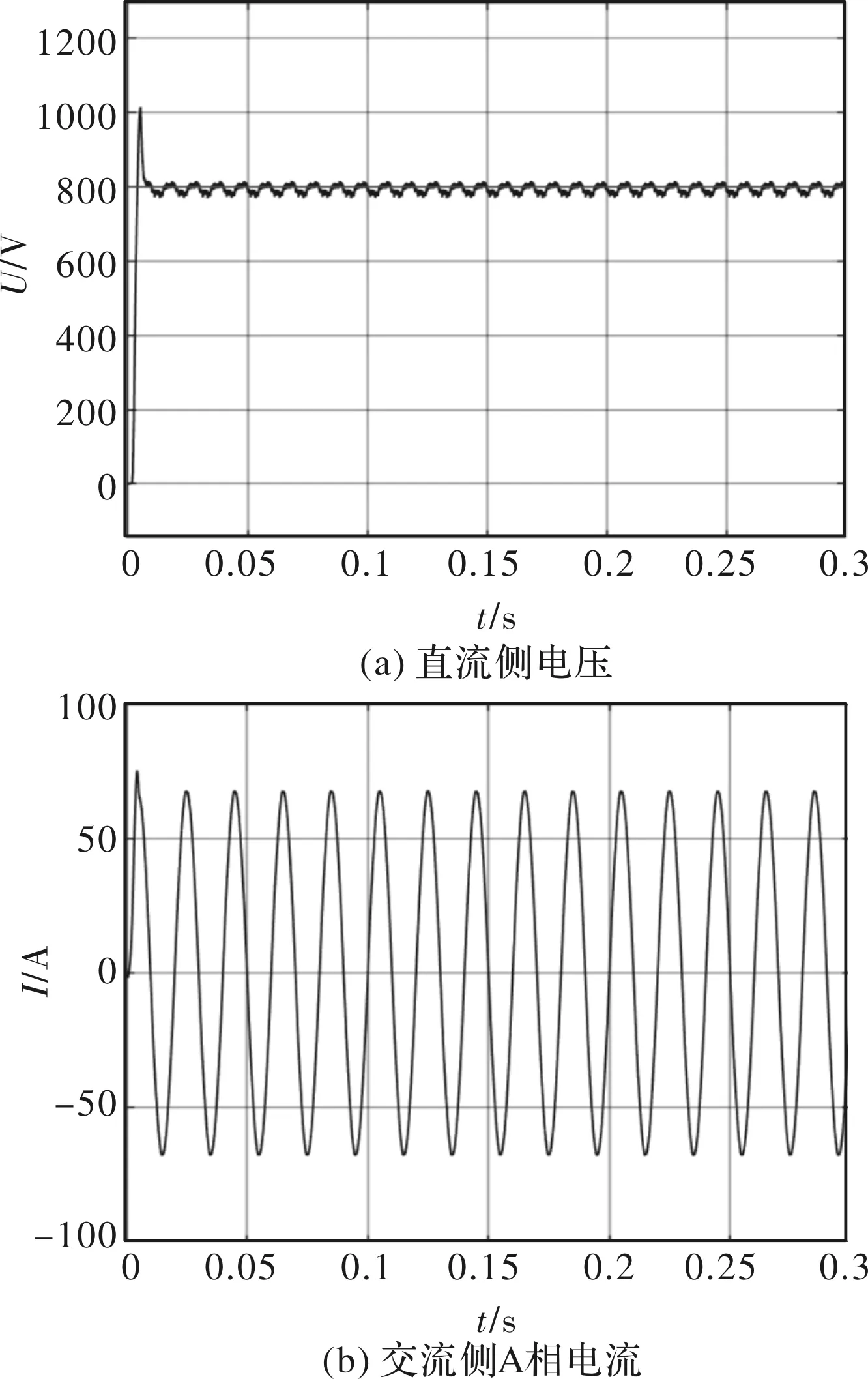
图8 电压电流波形图

由图9可以看出，在系统稳定后，能够以稳定的功率输出，虽然实际有功功率与参考有功功率存在一定波动，但波动很小，并且实际输出有功功率能够很好的追踪参考输出功率如图9(a)所示。无功功率虽无法达到零，但以较小值在零附近波动如图9(b)所示。

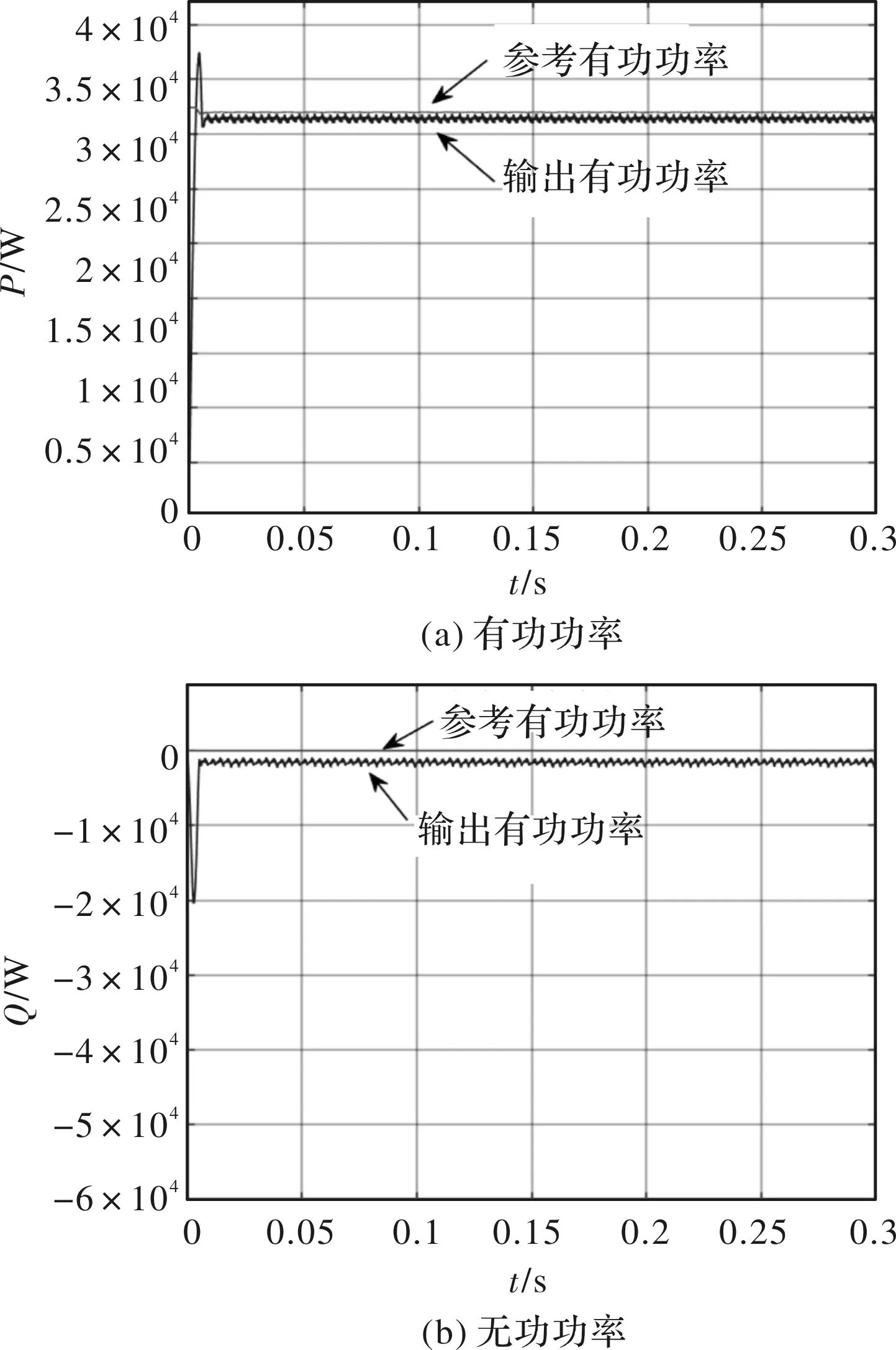
图9 输出功率

由图10可知，系统功率因数能够维持在0.99附近，即系统能够在单位功率因数下运行如图10(a)所示。对A相电流稳定后t=0.3 s后的3个周期的仿真波形进行分析，从傅里叶分析图可以看出， A相电流的电流基波幅值为67.84 A，电流的畸变率THD=0.84%如图10(b)所示。通过对系统功率因数分析及谐波分析，能够再次证明该控制策略能够极大减少对交流电网的污染。

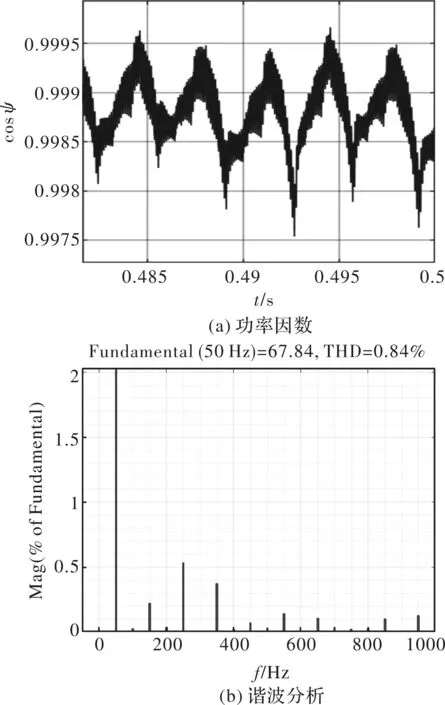
图10 功率因数及谐波分析

4 结 论

本文以双Y移30°非对称六相永磁电机九开关驱动/充电集成化拓扑结构为研究对象，结合拉格朗日插值法、滑模控制及SVPWM技术，提出了一种在充电模式下改进的预测型直接功率控制算法。通过简单的硬件配置，该方法能够将九开关变换器和电机合并在充电过程中，从标准三相交流电直接进行充电，实现了完全集成车载充电。相比与传统的直接功率控制，本文提出的算法响应速度更快，功率因数更高，对电网的污染更小。通过Matlab/Simulink仿真验证，当系统工作在充电模式下，电机无扭矩产生，系统能够输出稳定的直流电压，并在单位功率因数下稳定运行。