一种新型弧形磁场调制永磁电机的设计与分析

李建明

(湖北交通职业技术学院，武汉 430079)

0 引 言

在天线扫描系统、机械臂、雷达系统、天文望远镜等高精度应用场合中，往往需要驱动系统在特定角位移内沿弧线做往复运动。传统实现有限角位移的方法大多为蜗轮蜗杆或齿轮箱+旋转电机等间接驱动方式。然而采用间接驱动方式不仅占用较大空间，还存在传动误差大、响应速度慢、结构复杂等不足。而采用弧形永磁电机直接驱动的方式具有中间传动环节少、传动刚度高、安装要求低、易于维护等显著优势[1]，已得到国际学术界与工业界的广泛关注[2-3]。

弧形电机的转子侧与传统旋转电机的转子结构相同，而定子侧分若干块，每块呈弧形，定子块间彼此独立，均匀分布于圆周上[4]。由于定子侧的不连续，造成了弧形电机转矩波动较大，而转矩波动决定着定位精度与分辨率。与此同时，转矩密度则影响着电机的响应速度与加速度。因此，如何在不牺牲转矩密度的同时降低转矩波动，一直以来都是弧形电机领域的研究热点。

弧形电机的转矩波动主要来自于三大方面[5]：①边端效应；②齿槽效应；③绕组不对称效应。针对以上三大效应，降低弧形电机转矩波动的常规方法主要包括定子长度优化、永磁体形状优化、分数槽结构、斜槽/斜极、绕组换位等，下面将逐一进行介绍和分析。首先，从本质上分析，边端效应是由边端磁导的突变造成的，通过设计定子块长度为特定值可使定子块两侧的边端磁导突变作用互相抵消，从而降低转矩波动[5]。其次，弧形电机的齿槽效应与传统旋转电机的齿槽效应相同，也是由定子齿槽与永磁体相互作用产生的，因此也可采用类似的措施进行改善，比如斜槽/斜极[5]、永磁体极弧/厚度优化[6]、分数槽结构[7]等。如前面所述，弧形电机的定子不同于传统旋转电机，其定子分块使得绕组分布不对称，因而三相绕组反电势存在负序谐波，当通入理想的三相对称电流时会导致带载转矩波动较大。因此，文献[8]采用定子绕组换相位相连的方法来解决三相绕组不对称的问题，从而降低了总转矩波动。

以上传统方法均可有效降低弧形电机的转矩波动，但大多也带来了负面影响，例如转矩密度降低、加工难度提升、电机复杂度增加等。相关研究表明，磁场调制电机可在同等电磁负荷水平下，大幅提升转矩密度、降低转矩波动，同时电机复杂度基本不增加[8]，因此本文将弧形电机与磁场调制电机相结合，提出一种新型弧形磁场调制永磁电机，目的是在提升弧形电机的转矩密度的基础上，降低转矩波动。首先本文将介绍其运行原理，然后进一步分析关键设计参数对其主要电磁性能的影响，最后将新型弧形磁场调制永磁电机与传统弧形永磁电机进行对比。

1 工作原理

本文提出的新型弧形磁场调制永磁电机结构如图1所示，其转子表贴永磁体，定子分为N块(本文以三块为例)，每块定子采用开口槽，电枢绕组型式为环形绕组，绕制在定子轭上，以缩短端部长度。

图1 新型弧形磁场调制永磁电机

三块定子的电枢绕组可以由各自独立的变频器控制，以提高容错性和可靠性；也可相互串联或并联起来由同一个变频器控制，以节约系统成本。新型弧形磁场调制电机也是基于磁场调制原理[8]工作，其极槽配合需要满足：

pr=Ns±pa

(1)

式中，pr为每块定子正对的转子永磁体极对数，Ns为每块定子槽数，pa为每块定子中绕组极对数。表1总结了新型弧形磁场调制电机可采用的部分极槽配合，其中极比=pr/pa，每极每相槽数=Ns/6pa。

表1 新型弧形磁场调制永磁电机的极槽配合

为了详细解释该新型弧形磁场调制永磁电机的工作原理，以一台pr=5，Ns=6，pa=1的电机为例进行分析，其空载气隙磁密分析如图2所示。由于转子永磁体极对数pr=5，所以空载气隙磁密的主要磁对数为5。5对极气隙磁场经过6个定子齿的调制作用，在定子轭部产生了(6-5)=1对极的轭部磁密。为了使绕组正好能交链1对极轭部磁密，所以绕组极对数须满足pa=1。从而1对极轭部磁密就可以在1对极绕组中感应产生反电势，通入三相对称电流后即可产生恒定转矩。以上即单块定子的工作原理。

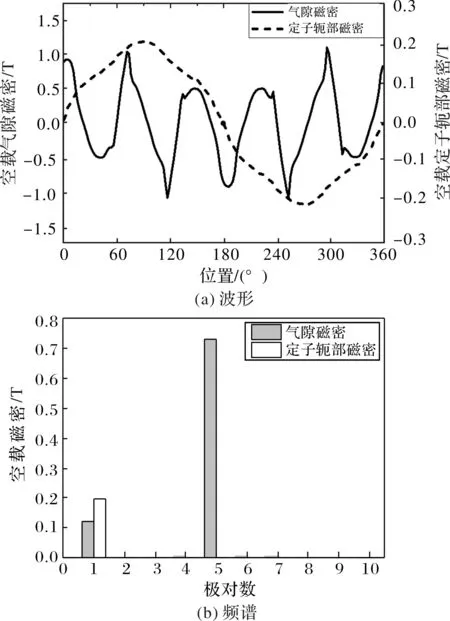
图2 空载气隙磁密和定子轭部磁密

对于多块定子的情况，由于不同块定子相对于转子永磁体轴的位置是固定的，所以不同块定子绕组产生反电势的大小和相位均一致，三块定子产生的转矩可以叠加，总转矩即为三块定子产生转矩之和。

2 设计参数优化

新型弧形磁场调制电机的设计过程分为以下两大步骤：

(1)全模型设计：在定子不分块(即完整定子)的情况下，优化极比、裂比(=定子内径/定子外径)、永磁体极弧、定子槽开口比率(=定子槽开口宽度/槽距)、永磁体磁极形状。

(2)分块模型设计：基于上述全模型的设计结果，将定子均分为六块，保留其中三块，如图1所示。然后优化三块定子的周向长度、三块定子间的相对位置，以实现最小可能的转矩波动。

需要说明的是，先采用全模型而后采用分块模型设计的原因为：分块模型的性能指标基本为全模型的一半，而全模型仿真时间更短，可大幅节约优化设计时长，因此在第一步中采用全模型代替分块模型进行优化设计。

新型弧形磁场调制永磁电机的原始模型参数如表2所示。从前面的分析可以知道，弧形电机最重要的两大性能参数即为转矩密度与转矩波动。因此，下面将分析各个设计参数对转矩密度与转矩波动的影响。

表2 新型弧形磁场调制永磁电机原始模型参数

2.1 极比

磁场调制电机性能最关键的设计参数即为极比，极比是转子永磁体极对数pr与定子电枢绕组极对数pa之比。图3分析了极比对额定转矩和转矩波动的影响。可以看到，随着极比的增加，转矩密度越来越低。这是由于极比增加，永磁体极对数变多，永磁体间漏磁增加，导致主磁通减小，因此额定转矩降低。还可以发现，转矩波动随着极比的增加也在逐渐减小。这是因为永磁体极对数变多，极数与槽数的最小公倍数增加，所以转矩波动变小。综合考虑下，本文选择极比为5。

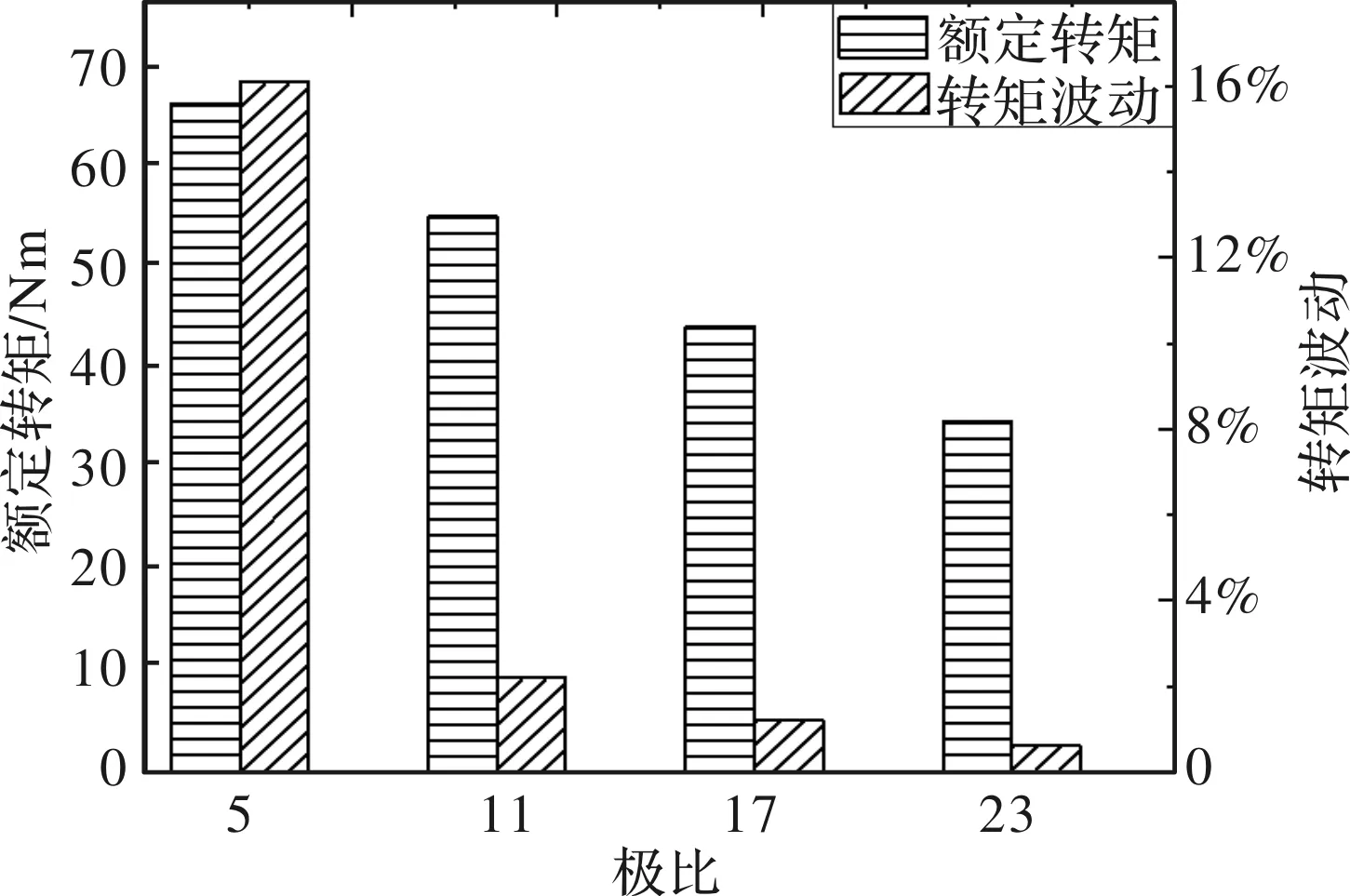
图3 关键性能参数随极比的变化

2.2 裂比

图4对比了不同裂比下的额定转矩与转矩波动。裂比为定子内径与定子外径之比，其值主要影响磁负荷与电负荷，而转矩密度正比于磁负荷与电负荷的乘积，因此影响着转矩密度。具体来讲，裂比增加，永磁体宽度增加，磁负荷变大；与此同时，裂比增加，定子内径变大，槽面积变小，电负荷变小。所以，随着裂比的变化，转矩密度有极值，如图4所示，在裂比=0.7时，额定转矩最大，此时转矩波动也处于可接受范围内，因此选择裂比为0.7。

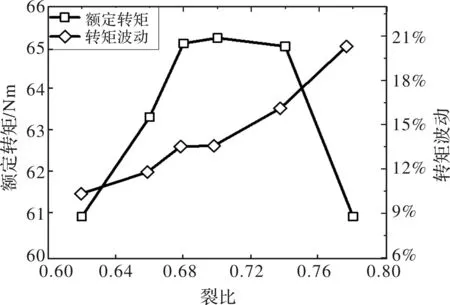
图4 关键性能参数随裂比的变化

2.3 永磁体极弧和定子槽开口比率

图5分析了转矩密度与转矩波动随着转子永磁体极弧和定子槽开口比率的变化，其中定子槽开口比率为定子槽开口宽度与槽距之比。可以看到，随着永磁体极弧的增加，永磁体宽度变大，磁负荷增加，所以额定转矩单调递增。然而，定子槽开口比率对额定转矩的影响并不是单调变化的。这是由于槽开口比率增加，等效气隙变大，主磁通变小；与时同时，槽开口比率增加，磁场调制效应增强，槽面积变大，电负荷增加。因此，槽开口比率对转矩的影响是多角度的。综合考虑转矩密度与转矩波动两指标，本文选择永磁体极弧为0.8，定子槽开口比率为0.65。

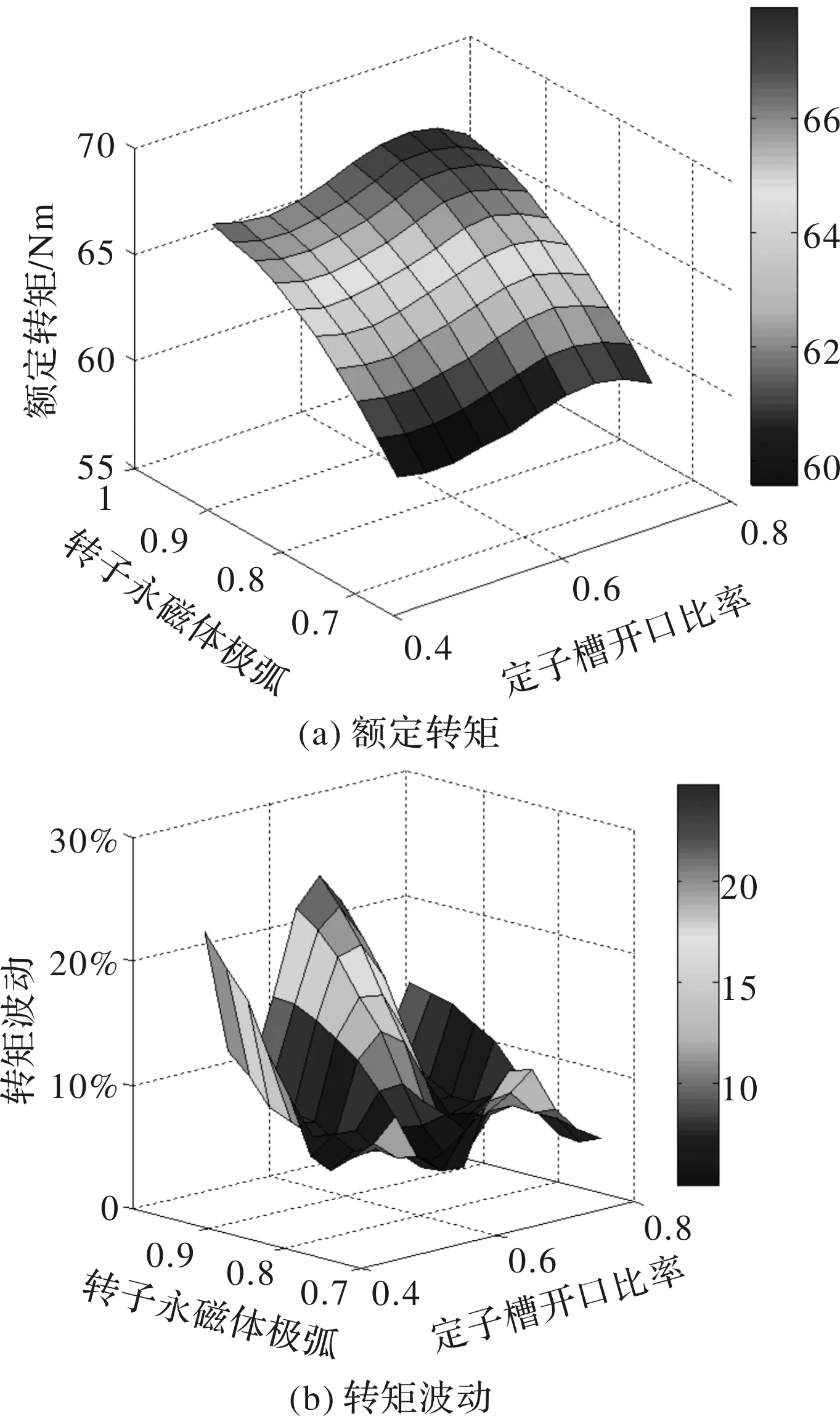
图5 关键性能参数随永磁体极弧和定子槽开口比率的变化

2.4 永磁体表面形状

为了进一步降低转矩波动，永磁体表面修形是常用手段之一。本文设置永磁体表面圆心相对于转子圆心有一偏移量，如图6所示，然后分析这一偏移量对转矩波动和转矩密度的影响，如图7所示。需要注意的是，优化过程中保证永磁体厚度不变，也即转子外半径不变以保持气隙宽度恒定。可以发现，随着偏移量增加，等效气隙增大，因此转矩密度持续减小。对于转矩波动来讲，偏移量先减小后增加。当偏移量为154 mm时，转矩波动达到最小值(约为2%)。

图6 偏移量定义

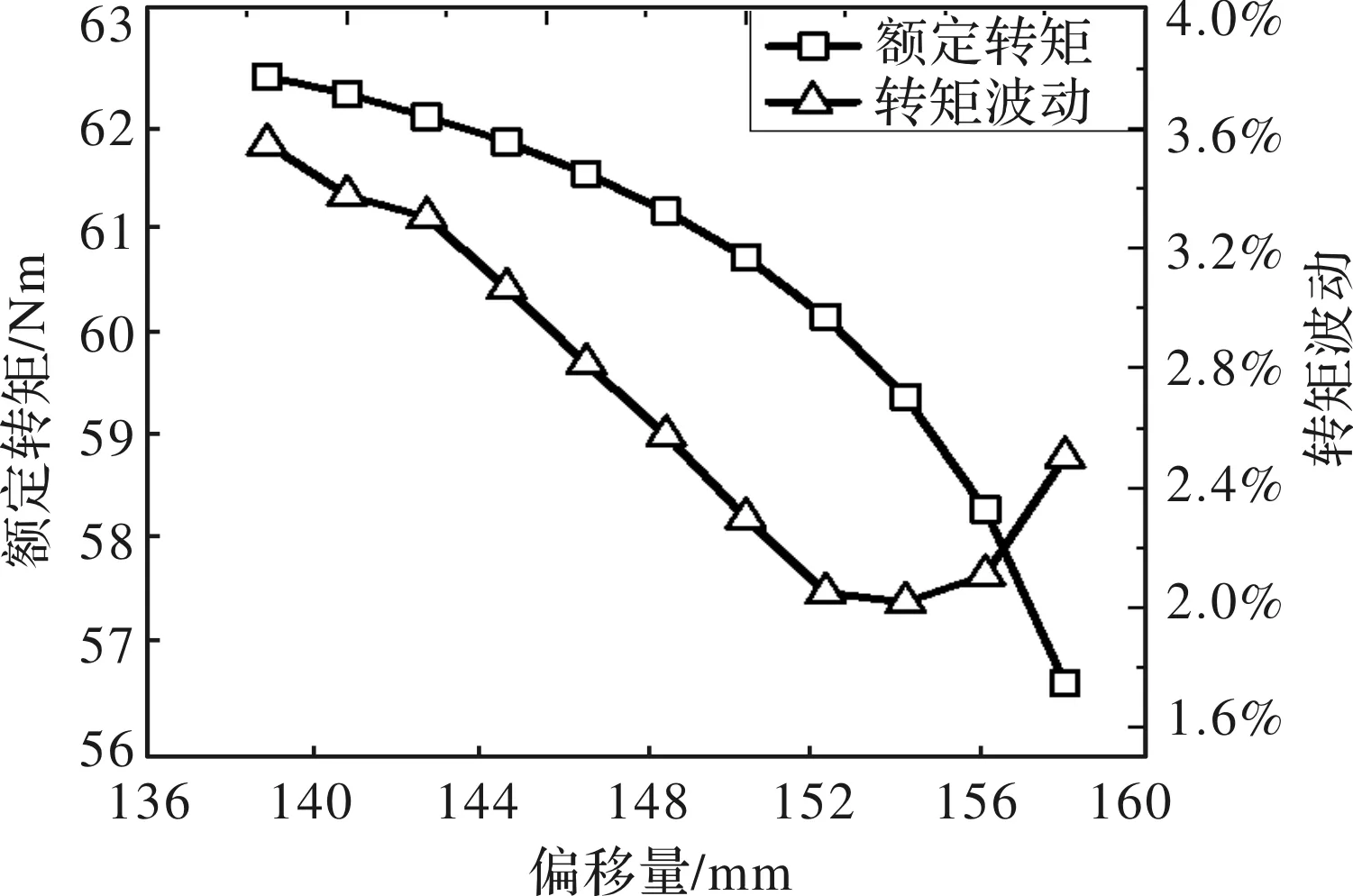
图7 关键性能参数随偏移量的变化

2.5 定子块周向长度

基于前面全模型的优化结果，本文把定子分为六块，留下对称的三块，如图8所示，以保证单边磁拉力为零。由于定子块两侧断开，因此会产生端部效应，而端部效应是转矩波动的主要来源[4]，因此本文将首先减小端部效应。对于单个定子块来说，其右侧端部所受拉力FR与左侧端部所受拉力FL可以写成：

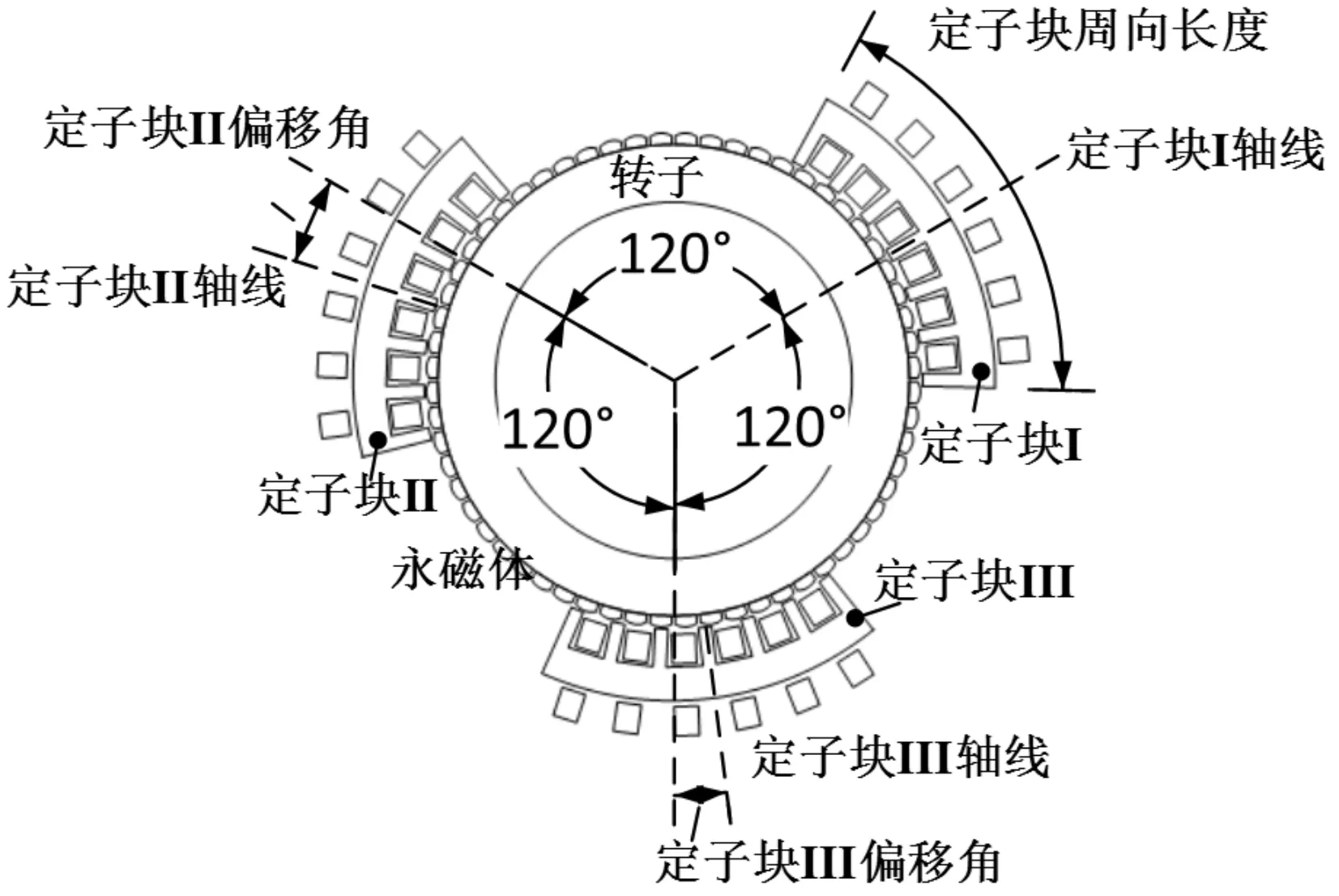
图8 定子块相关几何参数示意图

(2)

(3)

(4)

为了使定子块端部总拉力Fend最小，可以推导得定子块周向长度α应满足：

(5)

由于基波幅值最大，所以取n=1，则式(5)可写成：

α=(k±0.5)π,k=1,2,3…

(6)

为了验证式(6)所得到的定子块周向长度优化值，本文也采用有限元仿真的办法分析了定子块周向长度为转矩波动的影响。如图9所示，可以看到当定子块周向长度α=63°=10.5，转矩波动最小，因此解析分析与有限元仿真结果一致，本文取定子块周向长度为63°。

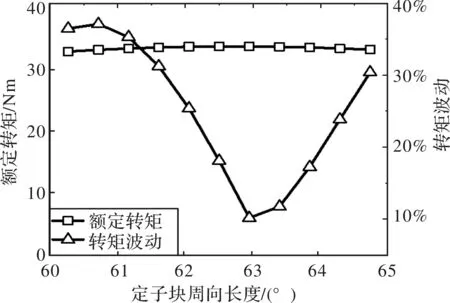
图9 关键性能参数随定子块周向长度的变化

2.6 定子块偏移角度

为了进一步降低分块后的转矩波动，本文提出一种定子块偏移法，具体来讲即是保持定子块I不动，使定子块II和定子块III各自偏移一个角度，使三个定子块产生的转矩波动相互抵消，最终使总的转矩波动最小。图10展示了额定转矩与转矩波动随着定子块II和定子块III偏移角度的变化。可以看到，定子块偏移对额定转矩影响不大，但对总的转矩波动影响较大。当定子块II偏移角为2°且定子块III偏移角为-2°(或定子块II偏移角为-2°且定子块III偏移角为2度)时，总的转矩波动最小，达到1%以下。

图10 关键性能参数随定子块II和III偏移角的变化

3 新型与传统弧形永磁电机对比

为了验证新型弧形磁场调制永磁电机的优势，本文将该弧形电机与传统弧形永磁电机[8]进行了对比。表3展示了两弧形电机的相关设计参数。为了使对比更具公平性，两电机具有相同的定子外径、叠片长度、热负荷、转子极数、永磁体用量等关键外部条件。需要说明的是，表3中极槽配合的不同来源于各自优化设计结果。新型及传统弧形永磁电机的空载磁力线分布如图11所示。可以看出新型弧形磁场调制电机的调制作用，在每块定子的轭部生成了2极的磁场。

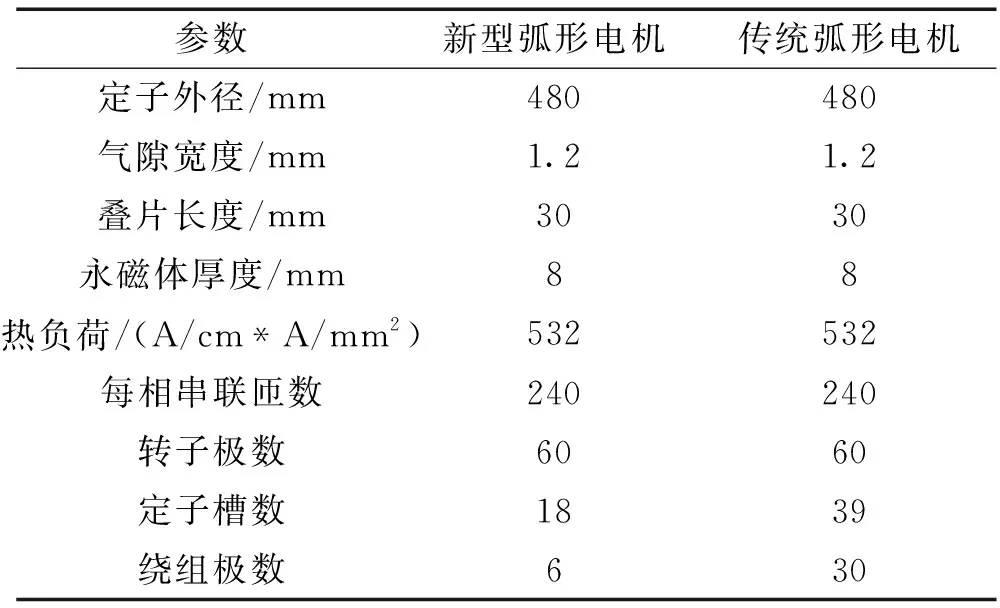
表3 新型与传统弧形电机设计参数

图11 新型与传统弧形电机的空载性能

如前所述，转矩密度与转矩波动是弧形电机最重要的性能参数，因此图12(a)和图12(b)分别对比了传统弧形永磁电机与本文提出的新型磁场调制弧形永磁电机的空载转矩及额定转矩性能。可以看到，新型弧形电机的齿槽转矩较低，波动为0.7%，是传统弧形电机的36.4%；额定转矩密度方面，新型弧形电机比传统弧形电机高出58.0%，同时转矩波动更小，降低近74%。因此，本文提出的新型磁场调制弧形永磁电机在减小转矩波动的同时，进一步提升了转矩密度。

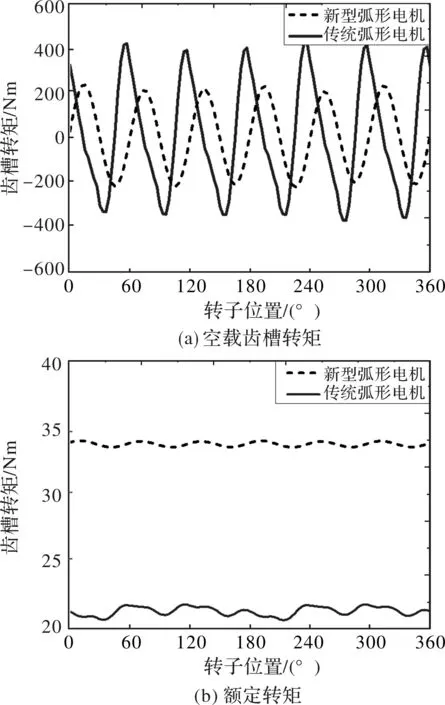
图12 新型与传统弧形电机的转矩性能对比

4 结 论

为了在不牺牲转矩密度的同时有效降低弧形永磁电机的转矩波动，本文提出一种新型磁场调制弧形永磁电机。在同样的电机体积与热负荷下，相较于传统弧形永磁电机，新型弧形永磁电机的转矩密度提升达33.2%，转矩波动降低约73%，有效提升了弧形电机的转矩性能。