U形截面PSRC梁预制构件受力性能试验和数值模拟

张 益 邵永健，* 易乐平

（1.苏州科技大学土木工程学院，苏州 215011；2.中亿丰建设集团股份有限公司，苏州 215131）

0 引 言

预制装配式型钢混凝土结构（Prefabricated Steel Reinforced Concrete Structure，简称 PSRC结构）是一种新型结构，可实现工厂预制、现场浇筑组装的工业化生产，且具有设计灵活、施工简便等优点。

目前国内外对PSRC结构的研究还不充分。国内，杨勇教授课题组对PSRC梁的静力性能进行了试验研究，研究结果表明，PSRC梁试件的试验现象和最终破坏形态与整浇SRC梁类似，受弯和受剪性能与整浇SRC梁差别不大[1-2]。吕西林、范力等人对装配式预制混凝土框架结构缩尺模型进行拟动力试验，并对此类结构的抗震性能进行了总结[3]，提出PSRC结构的板梁连接节点应加强或采用柔性连接。天津大学李忠献教授团队对PSRC结构的节点抗震性能进行了试验研究[4]，研究表明，PSRC结构框架节点有很好的变形能力和耗能性能。国外有日本发明的SR-PC工法[5]，此工法改善了传统H-PC工法的缺点。韩国Seon-Chee Cark教授带领研究人员对MHS体系中的U形PSRC梁进行了低周反复加载试验[6]，结果表明，U形PSRC梁延性较好，耗能能力较强且型钢与混凝土界面未发生严重的黏结滑移。

本文在试验的基础上，使用ABAQUS对6个试验梁进行数值模拟分析，并与试验结果进行了对比，验证模型的合理性，并以此为基础扩充设计参数进一步探究其对试件受力性能的影响。

1 试验概况

1.1 试件设计

本次试验按照剪跨比、混凝土强度和型钢类型设计制作了6个试件。具体设计参数如表1所示，钢筋、型钢和混凝土材性实测结果如表2—表4所示。混凝土标准立方体试块与试件梁在同等条件下养护。截面分为正方形和矩形两种，具体尺寸见图1。混凝土保护层厚度为20 mm。纵筋采用2C18，箍筋采用A6@200。型钢采用型号为Q345的HN1实腹式型钢和NH2蜂窝式型钢。

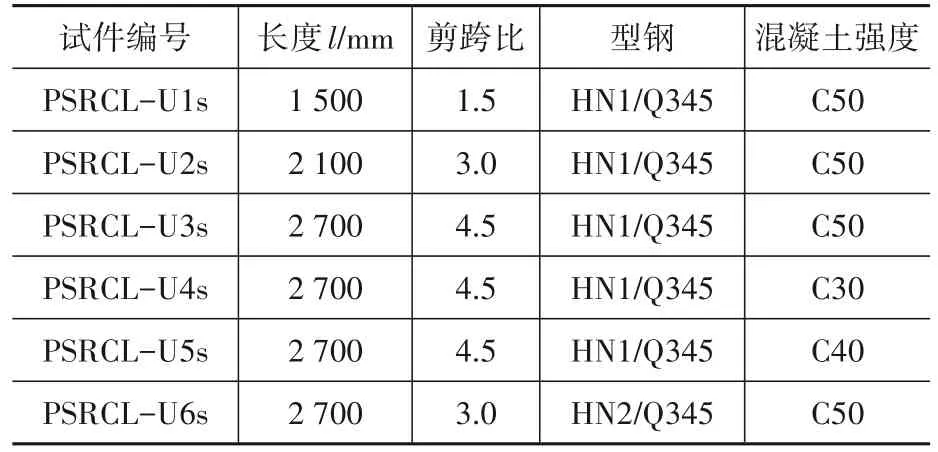
表1 试件设计参数Table 1 Specimen design parameters

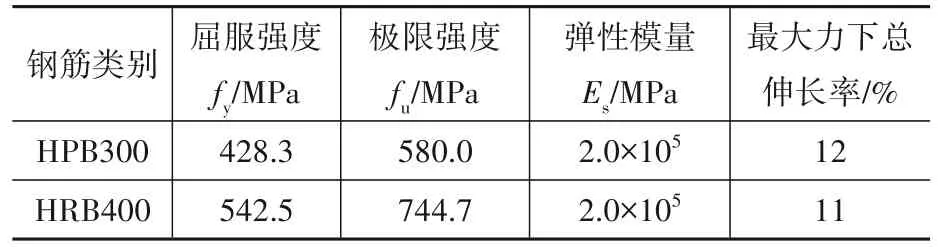
表2 钢筋实测力学性能指标Table 2 Measured mechanical properties of steel bars

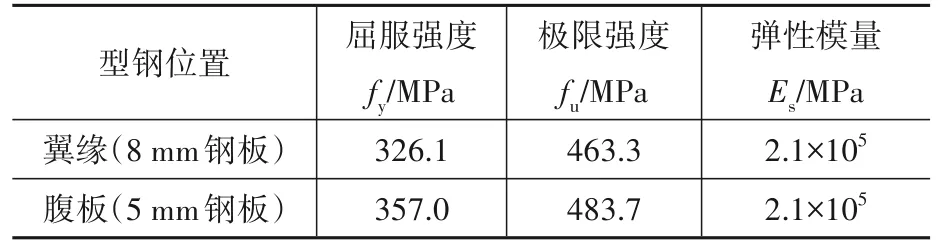
表3 型钢实测力学性能指标Table 3 Measured mechanical properties of section steel

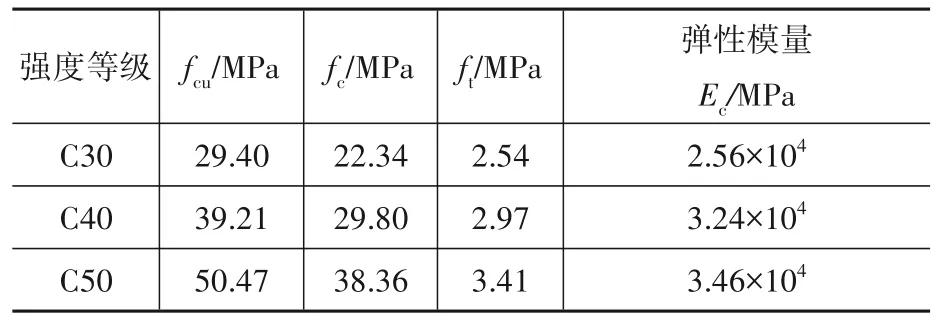
表4 混凝土实测力学性能指标Table 4 Measured mechanical properties of concrete

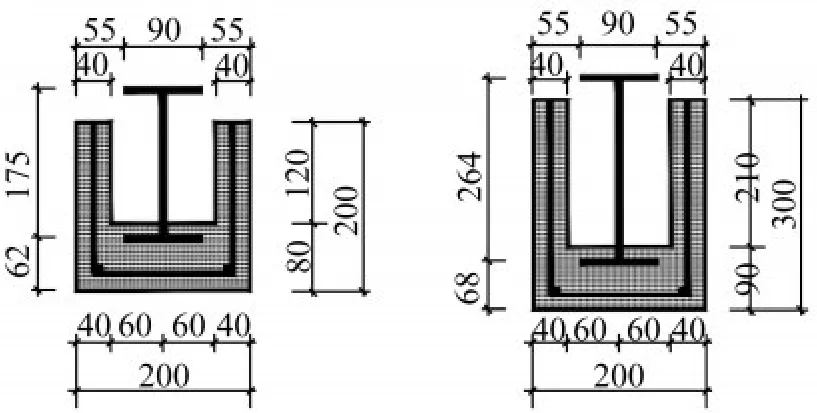
图1 试件截面尺寸（单位：mm）Fig.1 Section size of specimen（Unit：mm）

1.2 加载装置及加载制度

本次试验在江苏省结构重点实验室进行，加载装置见图2。采用力-位移混合加载方式，开裂前按极限荷载的5%加载，开裂后改为极限荷载的10%逐级加载至测力计示数不再变化，此时改为位移加载速率为0.5 mm/min，直到承载力降为峰值荷载的85%时停止加载。

图2 加载装置Fig.2 Loading device

1.3 试件主要破坏过程及特征

PSRCL-U1s发生了剪切斜压破坏。破坏过程及形态大致如下：当荷载加至80 kN时，梁两侧跨中纯弯段开始出现沿梁底向上发展的竖向裂缝，200 kN时弯剪段开始出现由支座向加载点外延伸的斜裂缝，随着荷载的增加，裂缝逐渐扩大并最终形成贯穿整梁的弓形主裂缝，此时支座处内侧边缘混凝土脱落，部分型钢上翼缘受压屈曲，如图3所示。

图3 PSRCL-U1s破坏形态Fig.3 Failure mode of PSRCL-U1s

PSRCL-U1s属小剪跨比试件，刚度大，发生斜截面的剪压和斜压破坏，破坏比较突然，混凝土提前退出工作，与型钢共同承载效果差，脆性破坏特征明显，因此与普通钢筋混凝土梁破坏模式有较大差别。

PSRCL-U2s至PSRCL-U6s均发生了受弯破坏。以U5s为例，破坏过程及形态大致如下：第一条裂缝出现在极限荷载的10%～15%，裂缝多集中在跨中纯弯段，随着荷载的不断加大，纯弯段处裂缝逐渐出齐但宽度不大，弯剪段出现斜裂缝长度较短，且斜向延伸不多。最终破坏形态为梁跨中上部混凝土被压溃脱落的同时型钢上翼缘局部屈曲，如图4所示。

图4 PSRCL-U5s破坏形态Fig.4 Failure mode of PSRCL-U5s

1.4 荷载-跨中挠度曲线分析

由图5可知，对比PSRCL-U1s、PSRCL-U2s和PSRCL-U3s，剪跨比是影响试件承载力的主要因素，随着剪跨比的增大试件承载力降低，但挠度增大延性和变形能力得到增强。对比PSRCL-U3s、PSRCL-U4s和PSRCL-U5s，混凝土强度的提高对试件承载力和刚度影响较小。对比PSRCL-U2s和PSRCL-U6s，配置蜂窝式型钢试件后期承载力不如实腹式型钢试件。

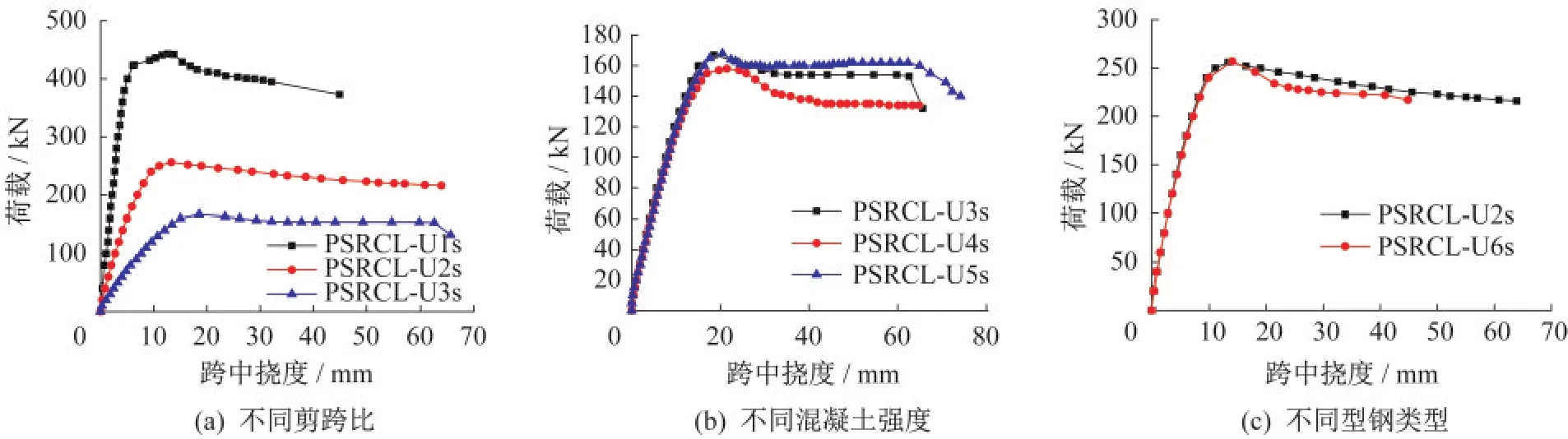
图5 不同试件参数对比图Fig.5 Comparison of specimens with different parameters

1.5 平面假定的验证

试件跨中截面混凝土和型钢应变沿截面高度变化如图6、图7所示。由图可知，中和轴位置随荷载增加变化不大，高度大体保持不变，加载过程中可认为平截面假定基本成立。

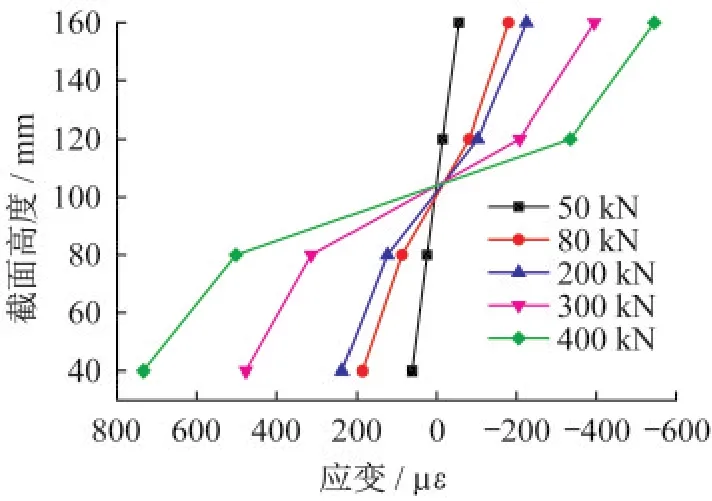
图6 混凝土应变沿高度变化曲线Fig.6 Concrete strain variation along height

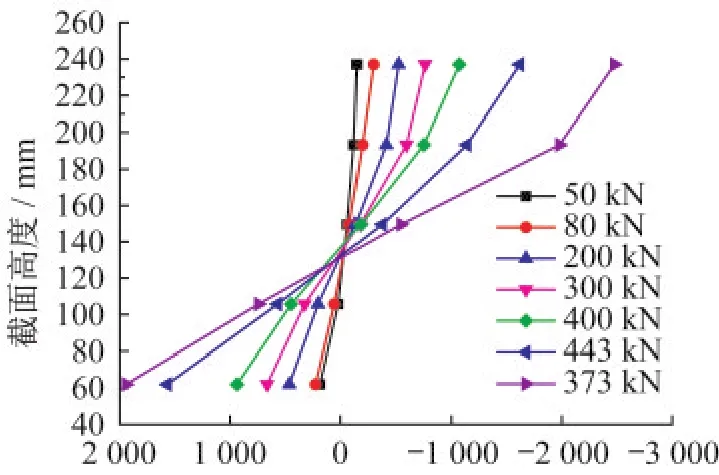
图7 型钢应变沿高度变化曲线Fig.7 Profile strain variation along height

1.6 裂缝与挠度

1.6.1 裂缝控制与刚度计算

本文研究的试件梁属于GB 50010—2010《混凝土结构设计规范》[7]中规定的第三级梁，允许出现裂缝的构件，需要控制裂缝和挠度。

试件梁受型钢包裹约束的混凝土较少，可以忽略，刚度叠加法不适用，采用规范[8]规定的式（1）计算刚度，计算结果如表5所示。

表5 刚度计算值Table 5 Calculated stiffness

式中各参数的含义及计算方法见规范[8]5.4.2条。

1.6.2 挠度验算

取试件屈服时跨中挠度试验值与按最小刚度法得到的计算值对比，结果如表6所示。

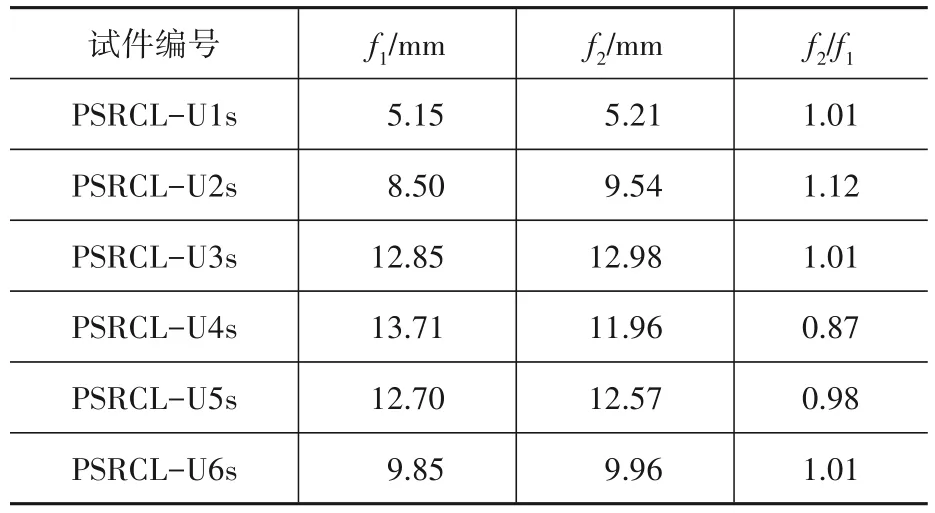
表6 跨中挠度试验值与计算值对比Table 6 Comparison of test and calculated values of mid-span deflection

由表6可知，屈服时试件跨中挠度试验值与按最小刚度法求得的计算值吻合较好，二者比值接近1，说明按规范[8]计算得到抗弯刚度是可行的，同时说明挠度计算的最小刚度法仍适用于本文研究的梁。

1.6.3 裂缝宽度计算

裂缝宽度计算采用规范[9]规定的式（2）计算裂缝宽度，荷载值取0.3倍极限荷载，计算结果如表7所示。

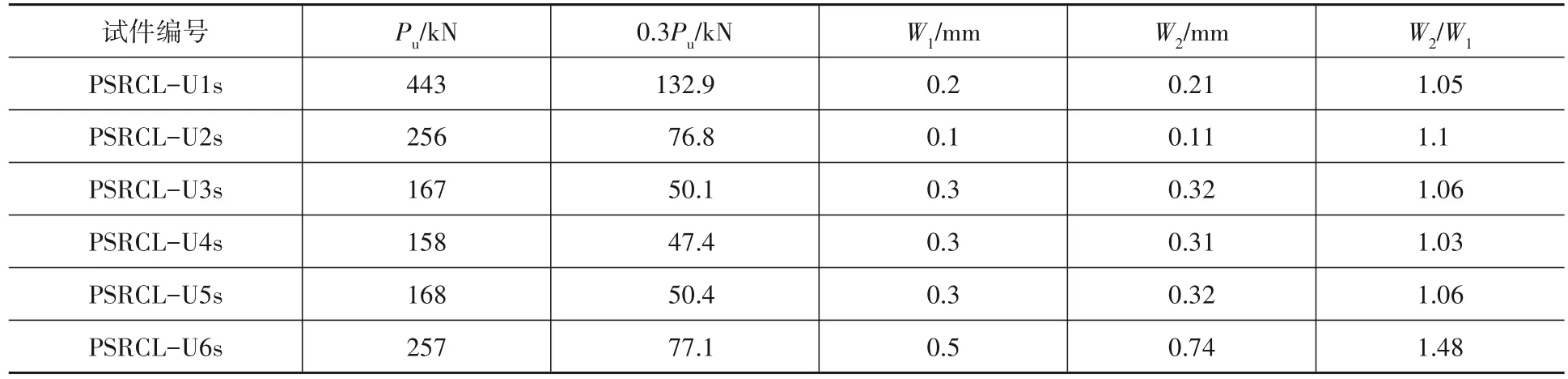
表7 裂缝宽度试验值与计算值对比Table 7 Comparison of experimental and calculated values of crack width

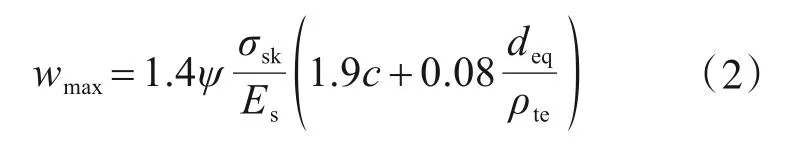
式中，各参数的含义及计算方法见规程[8]6.2.17条。

由表7可知，除PSRCL-U6s外，其他试件裂缝宽度试验值与计算值吻合较好，比值接近1，说明式（2）适合计算试件梁的裂缝宽度。

2 有限元建模过程

2.1 选择单元类型

根据材料特性和受力特点，混凝土采用八节点减缩积分单元，即C3D8R单元。型钢采用三维壳单元，即S4R单元。在加载过程中底部纵筋只受压力和拉力，因此模拟时只考虑其沿长度方向的变化。箍筋为不闭合状态，其作用只是与纵筋搭接形成钢筋骨架约束混凝土，几乎不受剪力作用。纵筋与箍筋采用二节点三维桁架单元，即T3D2单元。

2.2 材料本构模型

2.2.1 混凝土本构

本研究中混凝土本构关系采用GB50010—2010《混凝土结构设计规范》[7]附录C推荐的应力-应变曲线。

混凝土单轴受拉应力-应变关系按式（3）确定：

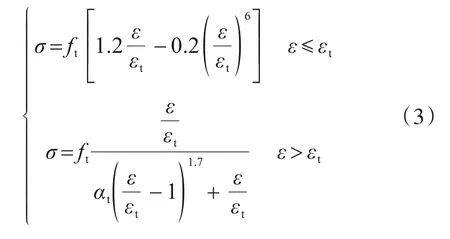
式中：ft为混凝土单轴抗拉强度；εt为混凝土峰值拉应变。αt为混凝土单轴受拉应力-应变曲线下降段的参数值。

混凝土单轴受压应力-应变关系按式（4）确定：

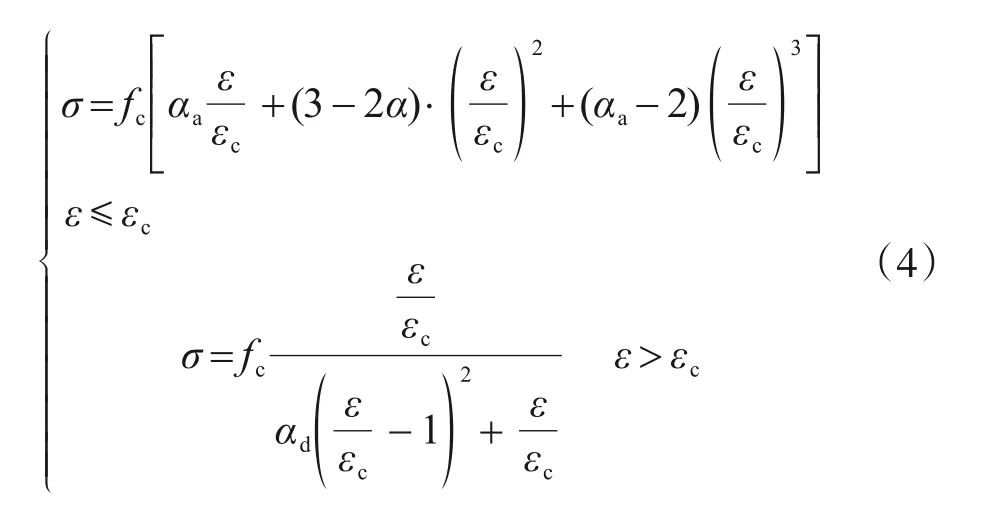
式中：αa和αd分别为混凝土单轴受压应力-应变曲线上升段和下降段参数值；fc为混凝土单轴抗压强度；εc为单轴抗压强度fc相应的混凝土峰值压应变。

2.2.2 钢材本构

本研究中，根据型钢、纵筋和箍筋的材料特性和受力特点，并考虑钢材的Bauschinger效应，型钢与钢筋采用等效理想弹塑性双折线模型，强化段的弹性模量取0.02E。为防止钢垫块在加载过程中出现较大的变形，故将钢垫块的弹性模量设置为型钢弹性模量的20倍左右，这样可忽略其弹性变形。

2.2.3 计算参数的设置

ABAQUS中的混凝土损伤塑性模型较混凝土弥散开裂模型能更好模拟试件在单调荷载作用下的损伤积累[7]，故本研究中所有模型均采用混凝土损伤塑性模型。

其中混凝土膨胀角ψ取38°，流动势偏量ξ取0.1，初始双轴受压与单轴受压屈服强度比值σb0/σc0取1.16，Kc取0.666 7，黏性系数μ取0.000 5，混凝土受拉损伤因子取0.5，混凝土受压损伤因子取 0.6[10]。

2.2.4 定义约束

由于型钢下翼缘与部分腹板位于混凝土梁内部，为了便于划分网格用一个平行于x-y的平面将型钢分割成外露和内置两部分，内置部分忽略与混凝土间的黏结滑移，采用Embedded约束。纵筋与箍筋形成的钢筋骨架完全内置于混凝土梁内部，同样采用Embedded约束。下部钢垫块采用Tie绑定约束。两个加载点RP-1和RP-2与型钢上翼缘相应位置采用耦合约束。划分网格时充分考虑ABAQUS在运算时的精度和效率，钢材网格尺寸取30 mm，混凝土网格尺寸取50 mm。

本模型中边界条件设置与试验相近，即上方约束U2，下方约束U1，U2，U3，UR3。建立好的模型如图8所示。

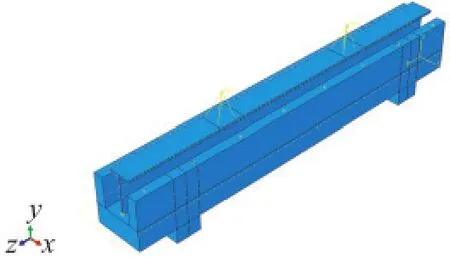
图8 有限元模型Fig.8 Finite element model

3 荷载-跨中挠度曲线分析

试验和模拟所得荷载-跨中挠度曲线对比见图9，特征值见表8。

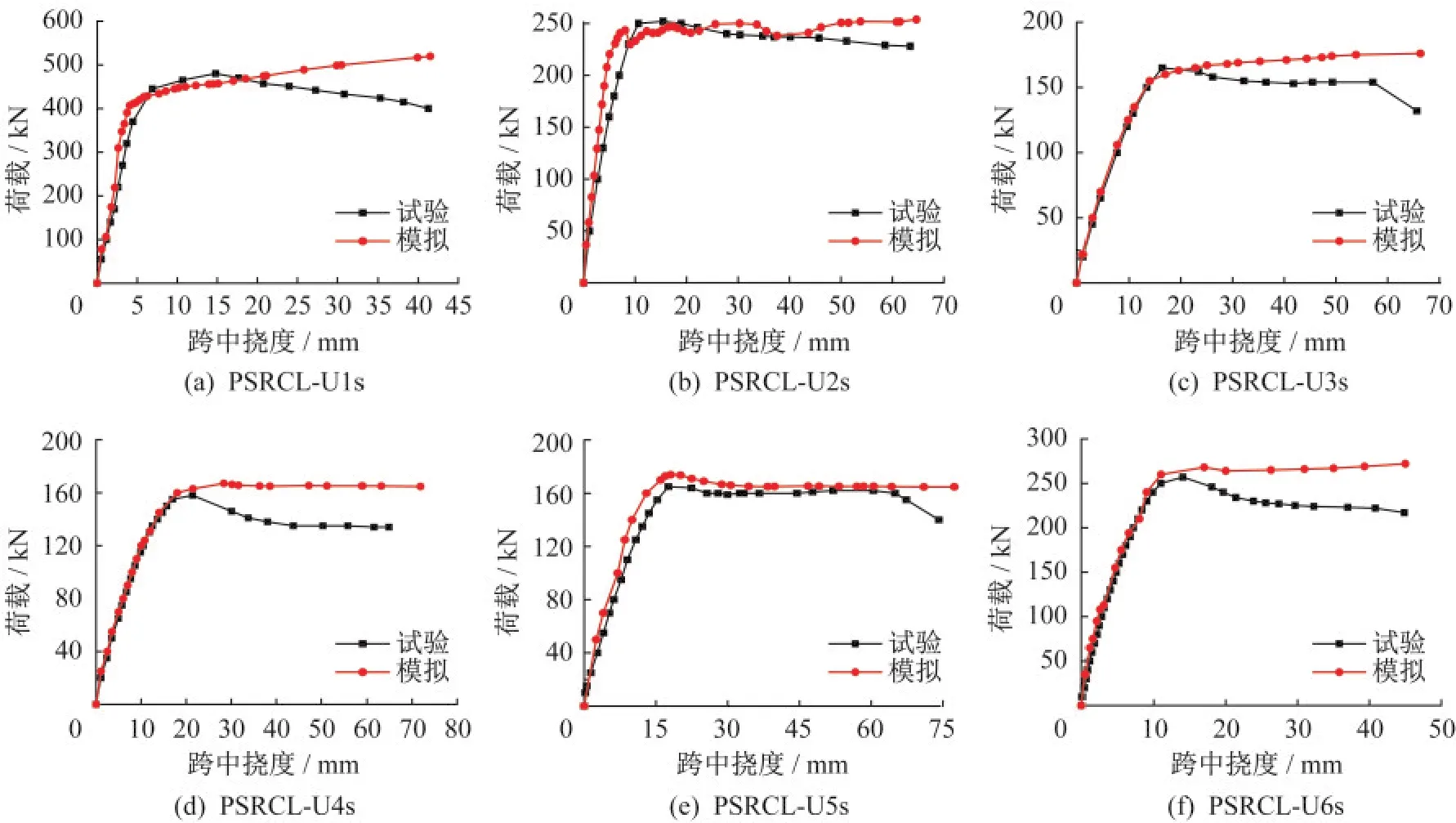
图9 荷载-跨中挠度曲线对比图Fig.9 Load-mid-span deflection curve comparison

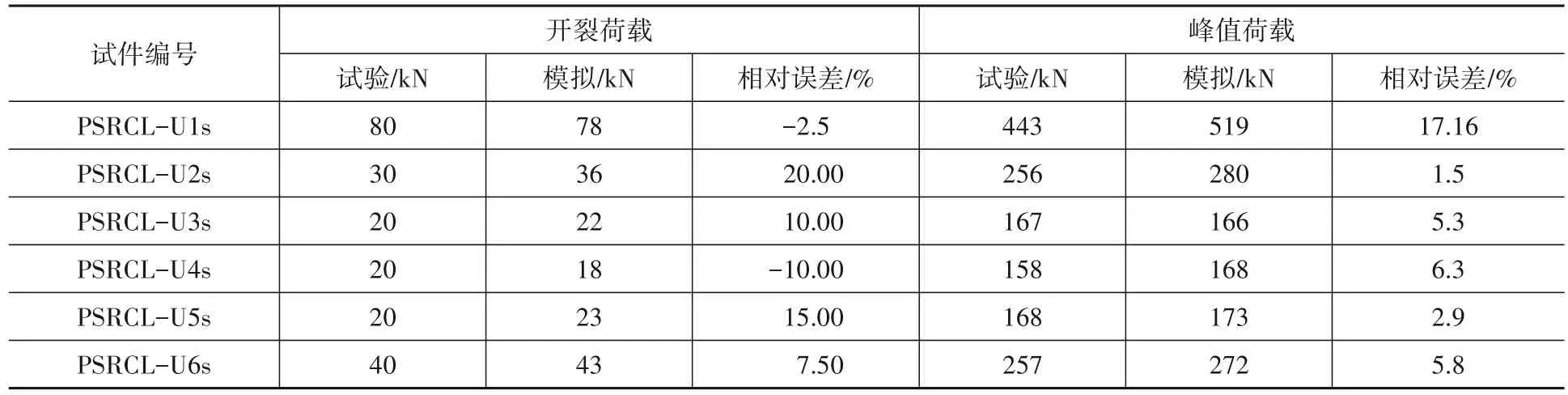
表8 荷载-跨中挠度曲线特征值对比Table 8 Comparison of characteristic values

由图9可知，试件达到屈服状态前，试验与模拟所得荷载-跨中挠度曲线总体较为接近，但本数值模拟也有不足之处，即后期曲线开始分离，相同挠度下荷载的模拟值均大于试验值，造成此差异的原因可能有以下三点：

（1）试件在浇筑过程中，人工搅拌、振捣的混凝土质量无法精确控制，导致梁体混凝土不完全均质而模拟中混凝土单元类型设置为Homogeneous（均质）。混凝土的浇筑对结果影响较大。

（2）试验后期混凝土基本退出工作，主要由型钢进行承载。ABAQUS中混凝土采用的塑性损伤模型是通过将每一级的损伤逐渐累积到下一级来模拟混凝土的受力状态，无法模拟混凝土的脱落，因此模拟曲线高于试验曲线。

（3）模拟中部分型钢和钢筋骨架内置于混凝土，钢垫块与混凝土下表面采用Tie绑定约束，均忽略了相对滑移。这与试验情况有出入，对模拟结果产生影响。

由表8可知，开裂荷载的试验值与模拟值存在一定差距，最大达到20%。分析如图10所示模型的应力云图得到开裂荷载模拟值，观察第一条裂缝出现得到开裂荷载试验值，二者取值方法的不同是误差产生的主要原因。除PSRCL-U1s外，其余试件峰值荷载误差较小，由于模型的局限性此差距难以规避。

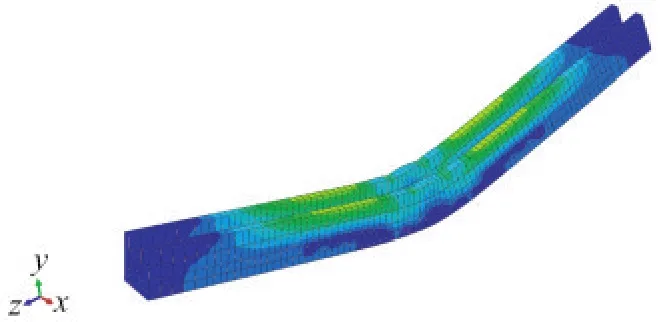
图10 PSRCL-U3s应力云图Fig.10 Stress nephogram of PSRCL-U3s

通过对比可知，试验值与模拟值总体上较为接近，说明用此方法来模拟U形截面PSRC梁预制构件的受力性能是可行的。

4 参数分析

在模拟和试验吻合的基础上继续对剪跨比、混凝土强度和型钢类型进行研究，同时在模拟的基础上新增配筋率来研究其对U形截面PSRC梁预制构件受力性能的影响。

4.1 剪跨比

图11为不同剪跨比试件荷载-跨中挠度的模拟曲线。

图11 剪跨比影响下荷载-挠度曲线对比Fig.11 Load-deflection curve comparison

分析图11可知，剪跨比为1.5的U1s刚度大承载力高但延性差变形能力弱。小剪跨比试件开裂较晚屈服强度高呈现脆性破坏特征。剪跨比为3.0的U2s和4.5的U3s刚度小、承载力低但延性好变形能力强。大剪跨比试件开裂较早，能很好发挥型钢的作用。

对剪跨比和极限承载力拟合，拟合曲线见图12。

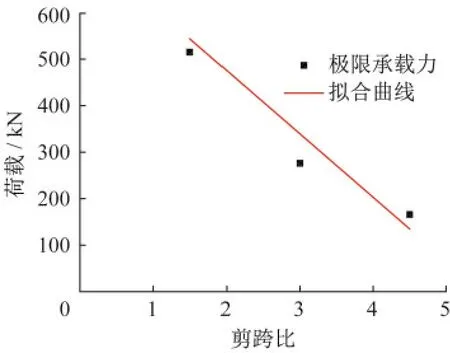
图12 极限承载力和剪跨比拟合曲线Fig.12 Fitting of ultimate bearing capacity and shear span ratio

拟合结果如下：

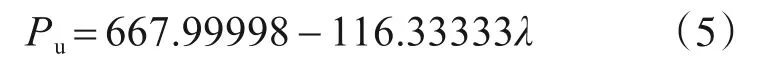
式中：Pu为极限承载力（kN），λ为剪跨比，拟合系数为0.912 88，说明极限承载力和剪跨比基本呈线性关系。随着剪跨比的增大承载力逐渐降低刚度变小，延性和变形能力提升。

4.2 混凝土强度

试验设计了C30、C40和C50三种混凝土强度等级，模拟增加C20和C60两种，以U3s为基准试件，所得荷载-跨中挠度曲线如图13所示。

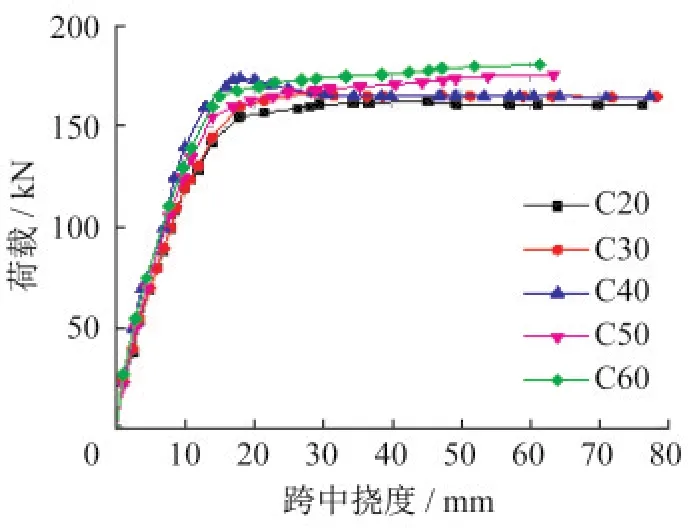
图13 混凝土强度影响下荷载-挠度曲线对比Fig.13 Comparison of concrete strength load-deflection curves

由图13可知，曲线前期高度重合后期分离但相差很小，总体上较为接近。因为U形截面上部受压区混凝土用量少，下部受拉区开裂后多由型钢和纵筋承载，因此提高混凝土强度对构件刚度、承载力和变形能力作用不大。

4.3 型钢类型

对配置实腹式型钢的PSRCL-U2s和蜂窝式型钢的PSRCL-U6s模拟分析，所得荷载-跨中挠度曲线如图14所示。

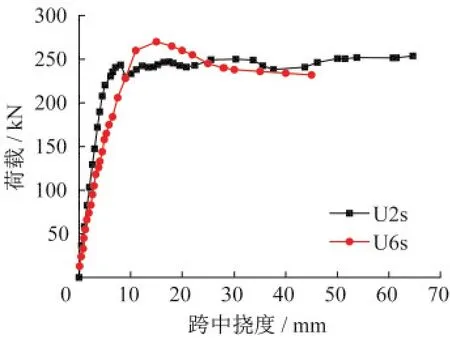
图14 不同型钢类型试件荷载-挠度曲线对比Fig.14 Load-deflection curve of different steel type specimen

由图14可知，U2s的承载力低于U6s，但变形能力强。蜂窝型钢与实腹型钢相比截面削弱很多，试件加载后期在截面削弱处被压曲，因此U6s后期承载能力于不及U2s。

4.4 配筋率

试验未将纵筋配筋率作为设计参数，模拟中引入1.22%、1.66%、2.16%、3.38%、4.09%、5.28%六种配筋率，所得荷载-跨中挠度曲线如图15所示。

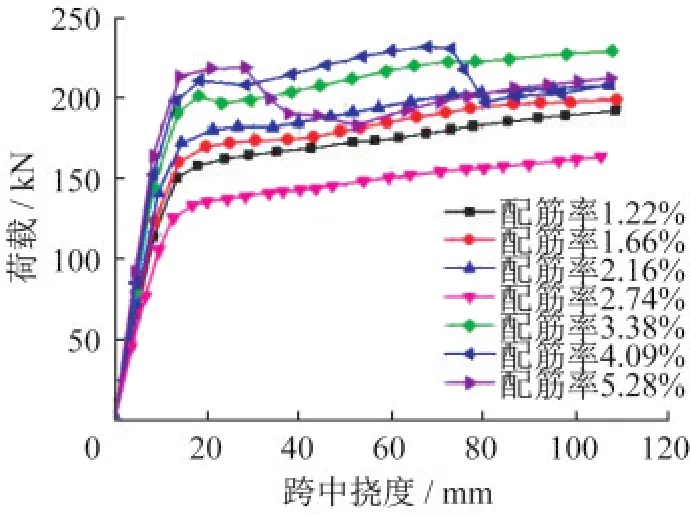
图15 不同配筋率荷载-挠度曲线对比Fig.15 Comparison of load-deflection curves with different reinforcement ratios

由图15可知，进入弹塑性阶段后各配筋率曲线开始分离，屈服后分离明显。配筋率为4.09%和5.28%的试件曲线前期高于其他配筋率，但在屈服后曲线出现弯折，说明提高配筋率能提升试件的刚度和承载力，但过高的配筋率会导致试件承载力突降，因此建议U形截面PSRC梁预制构件的配筋率不宜超过3.38%。

5 结论

（1）试验结果表明，与普通RC梁类似，剪跨比是影响U形截面PSRC梁预制构件受力性能的主要参数，剪跨比小的试件发生受剪破坏，剪跨比大的试件发生受弯破坏。混凝土强度和型钢类型对试件受力性能影响不大。

（2）试验过程中，试件梁中和轴高度基本不变，平截面假定成立；PSRC梁底部预制构件需控制裂缝和挠度，按规范[8]中公式计算试件梁刚度，并对挠度的试验值和计算值进行了对比，验证了挠度的最小刚度法适用于此试件梁；按规范[9]计算试件梁裂缝宽度与试验值接近。

（3）通过ABAQUS数值模拟得到的6个试件荷载-跨中挠度曲线与试验曲线较吻合，说明本文提出的方法能较好地模拟U形截面PSRC梁预制构件在单调荷载作用下的受力性能。

（4）通过参数分析可知，剪跨比增大试件承载力和刚度下降，但变形能力增强；混凝土强度对试件承载力和刚度影响不大；配置蜂窝式型钢试件挠度和后期承载力不及实腹式型钢试件；提高纵筋的配筋率能提升试件承载力和刚度，但不宜超过3.38%。