基于BP神经网络的预制柱套筒灌浆缺陷检测研究

马 毅 周德源 张 璇 韩 笑

（1.同济大学结构防灾减灾工程系，上海 20092；2.山东科技大学，青岛 266590；3.成都东部新区公共服务局，成都 641418）

0 引 言

随着社会经济快速发展，人们对建筑的生产效率和环境友好程度提出了更高的要求。装配式建筑由于构件质量好、施工速度快、绿色环保等优点，而被大力推广。

装配式结构形式主要有装配式框架结构、装配式剪力墙结构和装配式框架-现浇剪力墙（核心筒）结构等。套筒灌浆连接节点是一种广泛应用于各种实际工程的节点连接形式[1]。该方法具有传力形式好、不受钢筋直径影响、施工周期短等优点。在地震作用下，装配式混凝土结构的破坏主要出现在各构件连接的节点处。因此，预制构件的连接节点是装配式结构的薄弱环节，故而成为装配式结构抗震研究的主要对象。对于使用套筒灌浆方式连接的装配式混凝土框架结构，上下柱之间的连接节点质量不易得到保证[2-3]。因此，建立一种有效的预制框架柱套筒灌浆缺陷检测方法成为当前所需，以便于装配式结构的推广。

近年来，BP神经网络逐渐成为缺陷检测的一个重要工具，它拥有一定的容错能力、泛化能力以及自学习和自适应能力，并且可以映射任何非线性关系。本文通过使用此方法，对装配式框架柱节点处套筒灌浆连接的缺陷检测进行研究。

1 研究方法

2 模型介绍

ABAQUS是一款具有强大仿真能力的有限元软件，本文使用ABAQUS，依据框架柱的常见类型，分别建立底层边柱、顶层边柱、底层角柱、顶层角柱共4种柱子的有限元模型，如图1所示。预制柱采用250 mm×250 mm的矩形截面，高1 480 mm，混凝土强度等级为C30，纵筋和箍筋选用HRB400级钢筋，纵筋直径为12 mm，箍筋直径为8 mm；保护层厚度为20 mm；各层柱子的纵筋均通过套筒灌浆方式连接，在连接处布置20 mm厚的接缝灌浆层；框架柱的端部在不同约束下均设为固接。

图1 不同约束条件下框架柱的有限元模型Fig.1 Finite element models of frame columns with different constraints

本文采用激振方法进行缺陷检测，通过对结构施加激振荷载，来得到各测点的加速度时程响应。激振点和测点的位置如图2所示。各测点位置与纵筋逐一对应且按顺时针编号，激振方向在框架柱模型中为沿X轴负方向，激振荷载选择如图3所示。

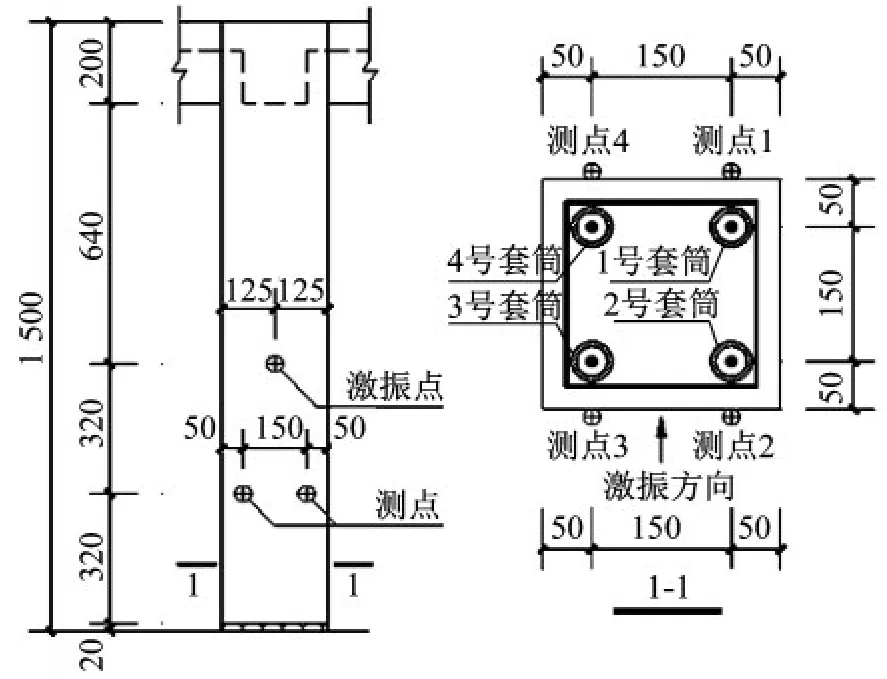
图2 激振点及测点布置图（单位：mm）Fig.2 Arrangement of excitation points and measuring points（Unit：mm）

图3 模拟锤击荷载Fig.3 Simulate hammer load

3 参数选择

与完好结构相比，缺陷结构的加速度动力响应会发生变化，导致信号频带各成分增强或抑制，从而使得各频带信息重新分布。因此当结构局部存在缺陷时，其附近的动力响应所包含的信息，即各频带的能量占比与完好结构相比会有不同程度的改变。利用小波包分解技术，可将目标信号分解到任意精度的频带上，对这些频带上的能量进行统计，并提取能量特征参数达到判别结构缺陷的目的。而基于小波包分解计算得到的结构缺陷参数能量比偏差（Energy Ratio Variation Deviation，ERVD），代表能量比变化相对均值的离散程度[7]。根据Zhang等[8]的研究，能量比偏差与装配式结构的套筒灌浆缺陷有较强的正相关性，且抗噪声能力好，故本文中神经网络选择作为输入参数。

对于以上4种预制柱，按照表1所示方法引入缺陷（表中0表示套筒灌浆饱满，1表示套筒未灌浆），以此作为BP神经网络的训练工况。根据缺陷柱和非缺陷柱相同测点处的加速度时程曲线，计算出能量比偏差。每根预制柱布置4个测点，故而每组工况可以得到4个数值，将其组成输入向量，同时输出参数选用未灌浆的套筒个数，以上述参数来训练神经网络。

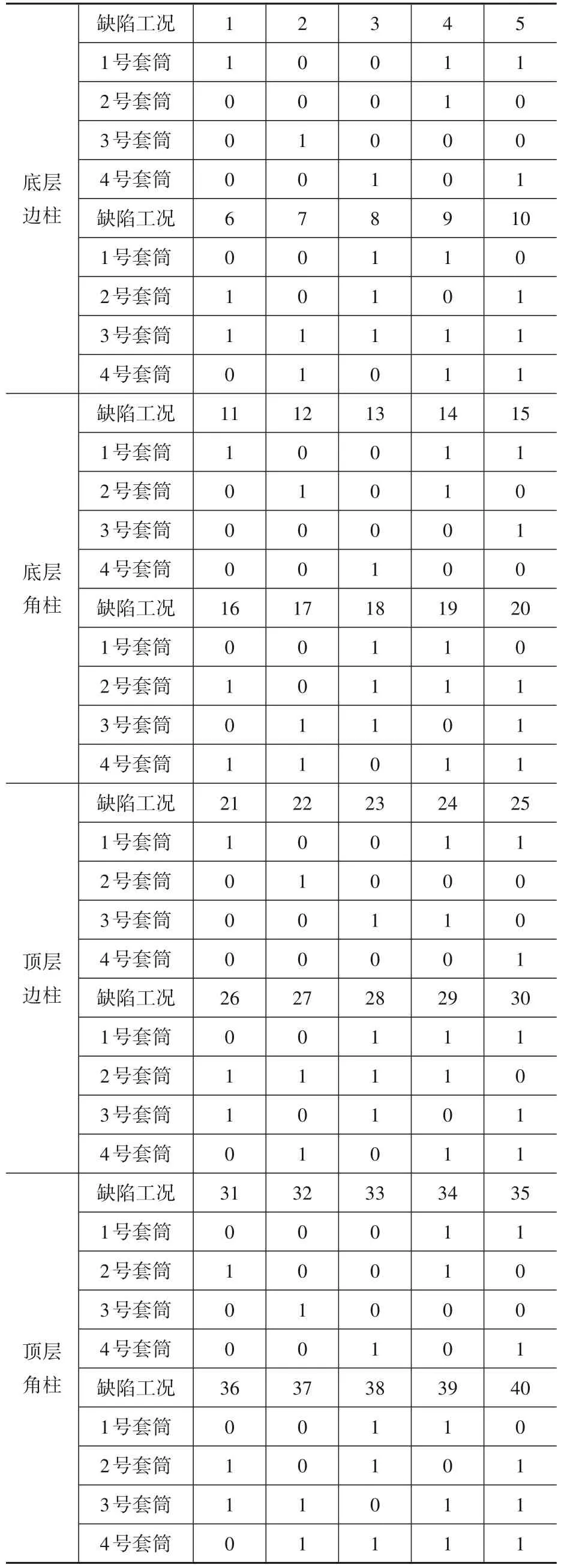
表1 训练工况下预制柱的缺陷引入情况Table 1 The introduction of defects in a precast column in training condition

4 训练及对比神经网络

Hecht-Nielsen[9]证明了对任意一个闭区间内的非线性映射，通过由输入层、隐含层及输出层组成的三层BP神经网络都可以完成逼近，因此本文BP神经网络采用三层网络结构，隐含层的单元数量，可按式（8）进行估算。训练神经网络的方法如图4所示。

图4 神经网络训练方法Fig.4 Neural network training method

式中：p表示训练样本数；q表示输出神经元数；h表示隐含层节点数；n表示输入节点数。

Matlab中有原始数据集可用于训练，包括训练集、验证集和测试集三部分。本文针对底层柱和顶层柱分别训练出两个神经网络，用于后续的缺陷检测。

4.1 使用原始数据进行神经网络训练

对底层柱和顶层柱，通过计算分别得到20组训练参数，将其作为输入参数用于训练底层柱神经网络（netB）和顶层柱神经网络（netP）。选用3层神经网络结构，10个隐含层单元，训练所得的均方误差（Mean Squared Error，MSE）、训练集（Training data）、验证集（Validation data）、测试集（Testing data）和总体（All）的回归分析结果如图5—图8所示。

图5 netB均方误差Fig.5 MSE of netB

图6 netP均方误差Fig.6 MSE of netP

图7 netB各数据集回归分析Fig.7 Regression analysis of netB data set

图8 netP各数据集回归分析Fig.8 Regression analysis of netP data set

对于底层柱，均方误差结果如图5所示，其值相对较低。将神经网络计算得到的输出值和各数据集的实际输出值进行回归分析，结果如图7所示。训练集、验证集和总体的相关系数R均接近1，而测试集的相关系数R约为0.85。结果表明训练得到的底层柱神经网络对缺陷的识别可以达到较高精度。

对于顶层柱，均方误差结果如图6所示，其值相对较低。将神经网络计算得到的输出值和各数据集的实际输出值进行回归分析，结果如图8所示。训练集、验证集的相关系数R均接近1，而测试集和总体的相关系数R仅为0.62和0.90。结果表明训练得到的顶层柱神经网络对缺陷识别的准确度并不十分理想。

4.2 使用含噪数据进行神经网络训练

为拓展训练数据，分别将水平为0.01%和0.02%的加性高斯白噪声根据式（9），将水平为0.1%和0.2%的乘性高斯白噪声根据式（10）引入到原始加速度响应数据中。

白噪声引入情况如表2所示，将4种不同的噪声引入到原始数据中，外加原始数据，底层柱和顶层柱的两个神经网络均可得到180组训练数据。

表2 白噪声引入情况Table 2 White noise introduction

对底层柱和顶层柱，将通过拓展所得到的180组数据分别用于训练底层柱神经网络（netB1）及顶层柱神经网络（netP1）。选用3层神经网络结构，80个隐含层单元。训练所得的SSE（均方误差）、Training data（训练集）、Validation data（验证集）、Testing data（测试集）和All（总体）的回归分析结果如图9—图12所示。

图9 netB1均方误差Fig.9 MSE of netB1

图10 netT1均方误差Fig.10 MSE of netP1

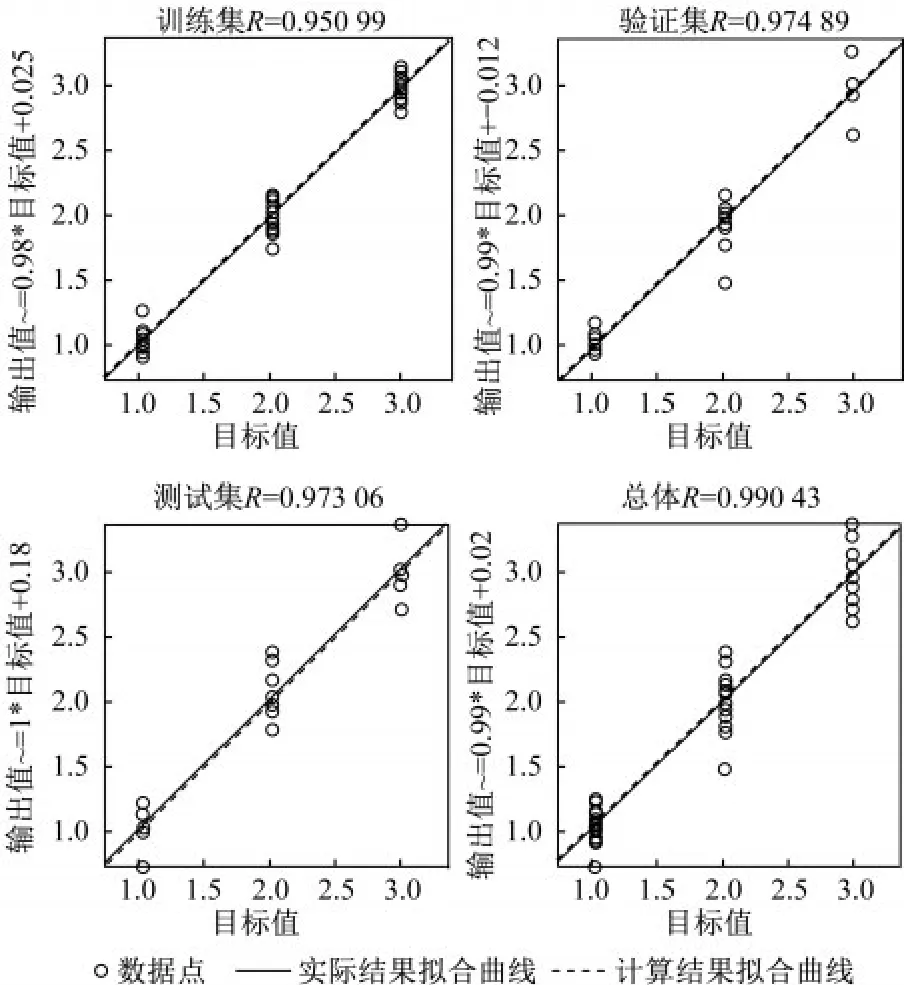
图11 netB1各数据集回归分析Fig.11 Regression analysis of netB1 data set

图12 netP1各数据集回归分析Fig.12 Regression analysis of netP1 data set

对于底层柱，均方误差结果如图9所示，其结果比netB所得结果更小。将神经网络计算得到的输出值和各数据集的实际输出值进行回归分析，结果如图11所示，四个数据集的相关系数R均接近1。结果表明用含噪数据训练得到的底层柱神经网络对缺陷的识别有更高的精度。

对于顶层柱，均方误差结果如图10所示，其结果同样比netP所得结果小。将神经网络计算得到的输出值和各数据集的实际输出值进行回归分析，结果如图12所示，四个数据集的相关系数R均接近1。结果表明用含噪数据训练得到的顶层柱神经网络对缺陷的识别精度有较大的提升，效果理想。

5 将神经网络用于缺陷检测

5.1 获取测试数据

现对上述训练所得神经网络用于套筒灌浆的缺陷检测。测试工况下预制柱数值模型的尺寸、配筋、激振点及测点布置等均与训练工况保持一致，但各柱的缺陷引入情况完全不同，如表3所示（表中0表示套筒灌浆饱满，1表示套筒未灌浆）。测试工况下，计算分析各测点的加速度时程响应，得到能量比偏差，将其作为上述训练得到的神经网络的输入参数。

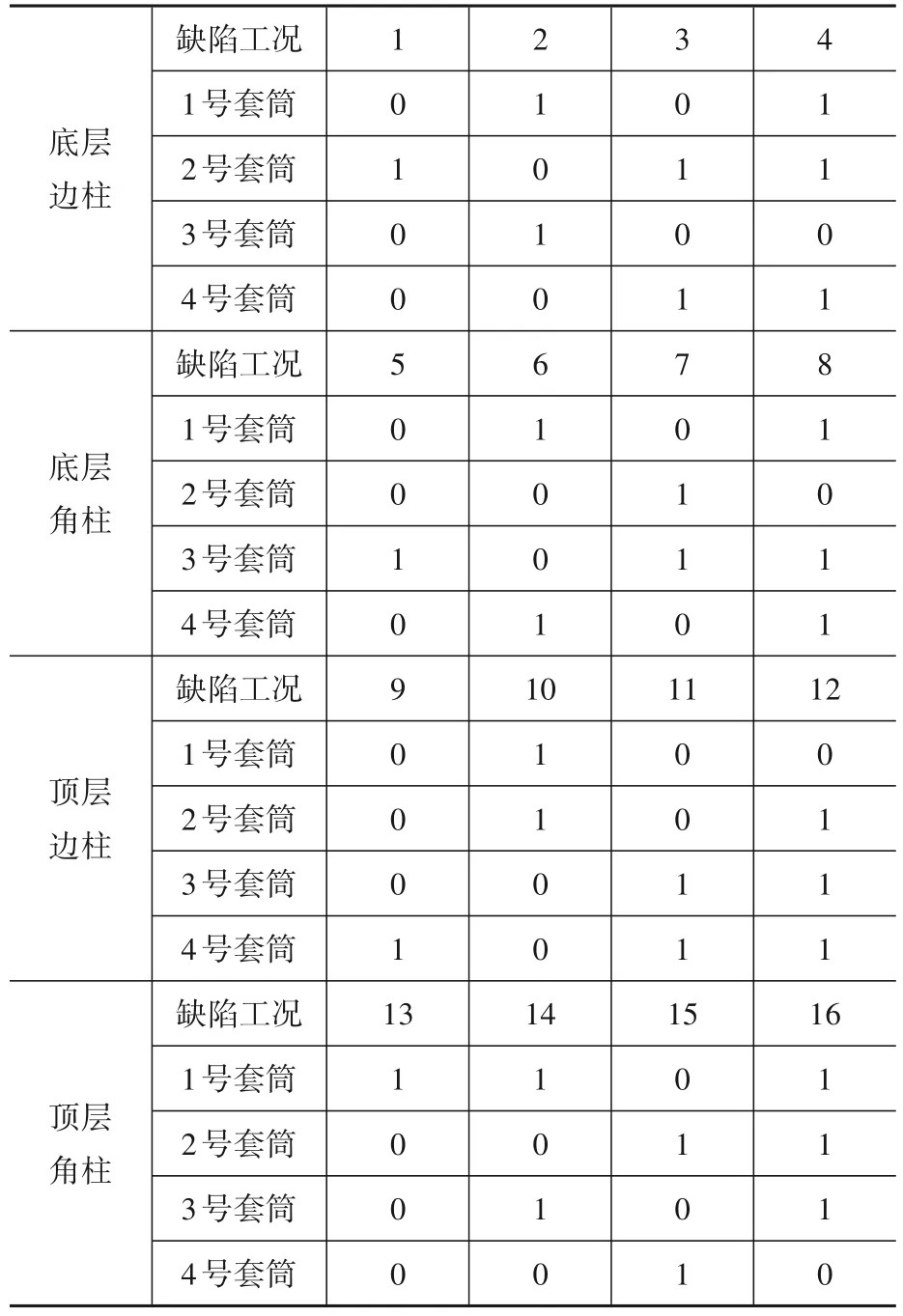
表3 测试工况下预制柱的缺陷引入情况Table 3 The introduction of defects in a precast columns in testing condition

5.2 神经网络检测原始数据

分别将用原始数据和含噪数据训练得到的两个神经网络用于预制柱缺陷的检测，并将二者的检测结果进行对比，如表4所示。

从表4中可以发现，不论是由原始数据训练，还是由含噪数据训练，二者所得到的神经网络输出的对未灌浆套筒个数的检测值与实际结果的误差都非常小，但前者与实际结果的相对误差整体来说大于后者。这表明将不同类型和水平的白噪声引入到原始数据中，在一定的程度上不仅可以拓展原始数据的数量及范围，同时可以提高神经网络的精度，还可以扩大神经网络的识别范围，增强泛化能力和鲁棒性等。

5.3 神经网络检测含噪数据

为研究神经网络的缺陷检测识别精度受不同类型和水平的白噪声影响的程度，分别在原始训练数据中引入水平为0.01%、0.02%、0.1%的加性白噪声，以及水平为0.2%、0.5%、2%的乘性白噪声，并通过式（9）和式（10）计算得到含噪测试数据。采用由前述含噪数据训练得到的神经网络（netB1、netP1）进行套筒灌浆缺陷检测，以研究测试数据中含有白噪声时对检测结果精确度的影响。计算结果见表5、表6。

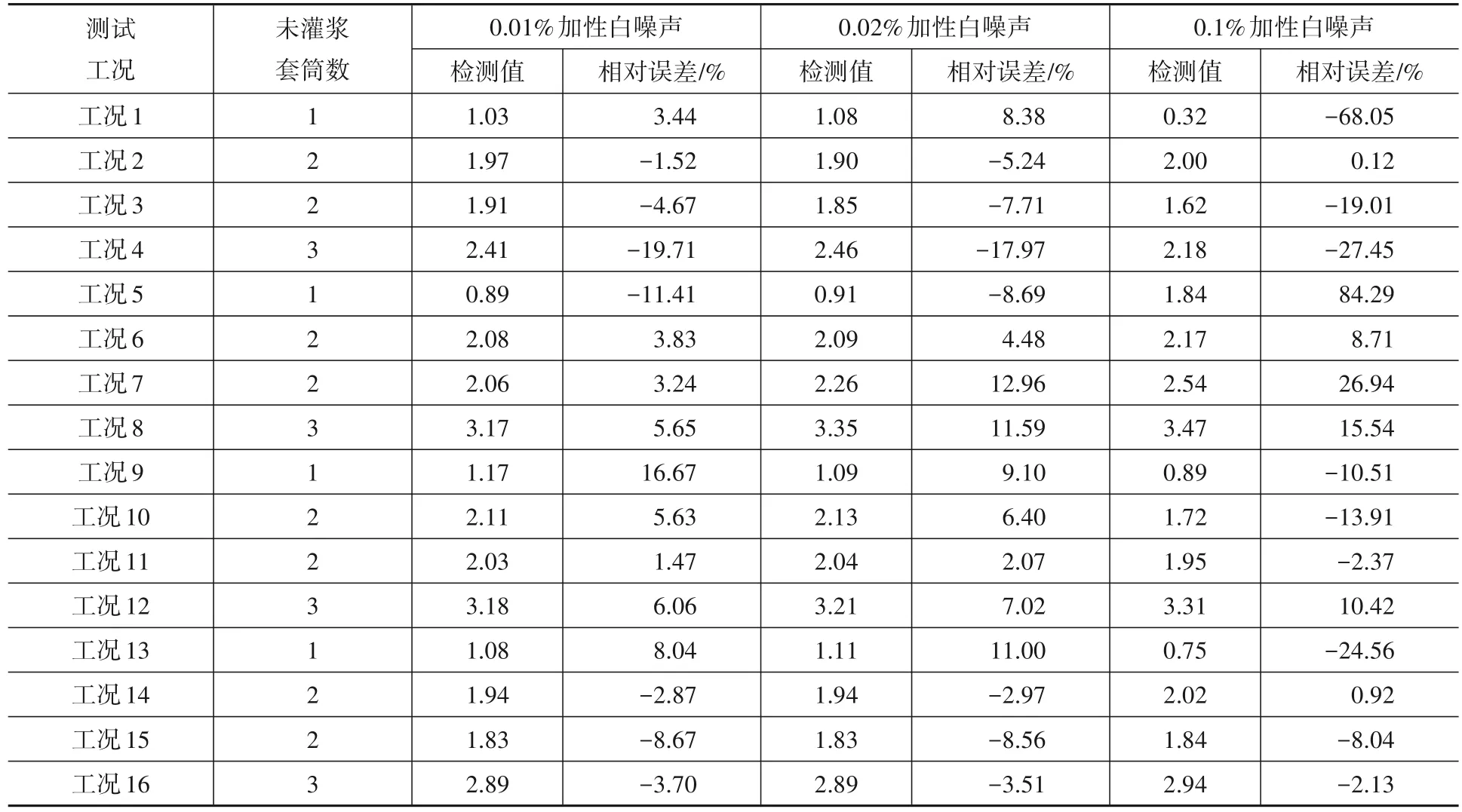
表5 含加性白噪声的测试数据缺陷检测结果Table 5 The result of test data contains additive white noise defect detection

表6 含乘性白噪声的测试数据缺陷检测结果Table 6 The result of test data contains multiplicative white noise defect detection

由计算结果可以看出，无论是含有加性白噪声，还是含有乘性白噪声，即使噪声水平相对较低，检测结果的相对误差仍然较大。因此，对尚需检测的数据，应在检测前对数据进行滤波处理，以减小检测结果的误差。

6 结论

本文利用有限元软件ABAQUS对4种不同约束条件的预制柱建立数值模型，在不同缺陷工况下，通过各测点在模拟锤击激励作用下的加速度时程响应，得到能量比偏差作为输入参数，以未灌浆套筒数目作为输出参数，采用BP神经网络进行套筒灌浆的缺陷检测。结论如下：

（1）在训练工况下，用原始数据训练得到的底层柱神经网络基本满足缺陷检测的要求，顶层柱神经网络的缺陷检测效果不是十分理想；用含噪数据训练得到的神经网络精度较高，均方误差及各数据集的回归分析结果相较原始训练数据都有所改善。

（2）在测试工况下，由原始数据以及含噪数据分别训练得到的两个神经网络，其缺陷检测识别的结果相对误差都很小，但前者和实际结果的相对误差整体而言大于后者。随着原始数据中白噪声水平逐渐提高，利用含噪数据训练得到的神经网络的缺陷检测识别精度越来越低。

（3）在实际工程应用中，对神经网络进行训练时，在训练数据中可以适当引入水平较低的白噪声，以扩大神经网络的识别范围，增强其泛化能力和鲁棒性。对尚需检测的数据，应注意在测试前是否对数据进行滤波处理，以减小缺陷检测结果的误差。