对于抗震设计规范设计反应谱的探讨和建议
杨 悦 施卫星 赵 昕 王梁坤 李晓玮,
(1.同济大学土木工程学院防灾减灾工程系,上海 200092;2.同济大学建筑设计研究院(集团)有限公司,上海 200092)
0 引 言
反应谱涉及的相关概念主要为“真”谱和“伪”谱,在国内外学术界均存在一些混淆使用的现象[1]。我国学者刘恢先早在1958年就明确提出采用反应谱理论,但是认为真谱与伪谱之间的关系是“精确”与“简化”的关系[2]。我国规范修订[3]过程中及近期的学术研究中[4]也仍然采用这种“精确”的真绝对加速度反应谱。但是“真”谱与结构设计理论并不协调,引起了诸多问题,包括反应谱随阻尼和周期增加出现大阻尼比的反应谱值大于小阻尼比的反应谱值,即“反超现象”。长周期设计反应谱与实际地震反应谱形状不符等[5-6]。
为改良现有反应谱存在的问题,学者们提出的一类改进方案为,对现行规范反应谱中的阻尼相关项调整,或直接对反应谱公式上叠加二次调整系数,曹加良等[7]对这些方法进行了分析,改进效果均不理想。另一类改进方案为,采用独立的长周期反应谱[8],但与现行规范的协调性差,无法用于指导结构设计。
由于反应谱是内力分析的基础和时程分析选波依据[9],此外,基于位移的抗震设计方法中需利用伪加速度反应谱与位移反应谱的关系进行转换[10-11],现行规范转换所得的位移反应谱无平台段,不能反映等位移原理[12],也不能指导长周期段的结构分析。随着我国长周期结构不断增多,提出物理意义明确且长周期段准确的反应谱曲线十分必要。
本文对反应谱相关概念的物理意义进行了分析,并利用简谐荷载双规准谱分析了地震反应谱的一般规律。最后对抗震设计反应谱的特征和影响因素进行了分析,并提出了对我国抗震设计反应谱的有关建议。
1 反应谱的相关定义
1.1 真伪反应谱的定义
结构运动方程如下式[13]:
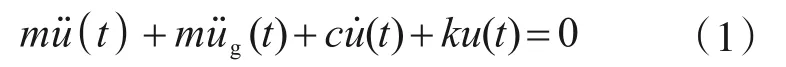
式中:m为质点质量;c为阻尼系数;k为结构刚度;u为质点相对于地面的运动;?̇为质点相对速度;为质点相对加速度;为地面运动加速度;t为时间。
1.1.1 真反应谱


1.1.2 伪反应谱
由于结构所受弹性力为ku=mω2u,所以定义伪加速度谱由位移谱转化而来,如式(5)所示。可见相对位移谱和伪绝对加速度谱能代表结构弹性内力,真绝对加速度谱反而不能代表结构内力。且振型分解反应谱法计算获得的结构位移和内力也与伪谱协调,与真谱反而不协调。
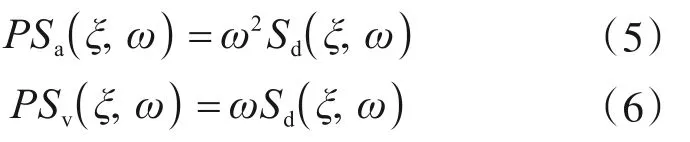
式中:p代表“伪(pseudo)”,PSa(ξ,ω)为伪绝对加速度谱;PSv(ξ,ω)为伪相对速度谱。如无特别定语说明,本文下文所述及的“加速度谱”或“伪加速度谱”均指由式(5)定义的“伪绝对加速度谱”,“速度谱”指由式(6)定义“伪相对速度谱”。
1.2 双规准反应谱定义
为了对结构地震响应进行更具通用性的研究,定义纵坐标为谱值与对应地面信号峰值的比值谱为标准反应谱,即放大系数反应谱,亦即“规准谱”。谢礼立等人将放大系数谱的横坐标进一步改为结构频率与峰值响应所在频率的比值即加载频率比的反应谱定义为“双规准反应谱”[3]。
由于地震动作用持时短,瞬态响应衰减不充分,故对地震简谐荷载作用分析时不可以忽略瞬态响应,应采用同时包含稳态和瞬态响应的全量响应进行分析。当结构受正弦简谐荷载作用时,可以推导得到结构全量响应与加载位移幅值的比值即标准化位移时程uN(t)如式(7)所示。

由式(12)、式(13)可知,稳态响应和瞬态响应的响应时程及幅值由阻尼比ξ和频率比β完全确定。且瞬态响应指数衰减项为e-ξωt,故当ξ为定值时,瞬态响应每个周期衰减的比例e-2πξ为定值,故稳态响应和瞬态响应合成的全量响应由阻尼比ξ、频率比β和加载周数P完全确定,响应幅值可以由下述公式表达。如图1所示,当上述要素相同时,加载周期分别为20 s和0.1 s的时程曲线形状完全一致。
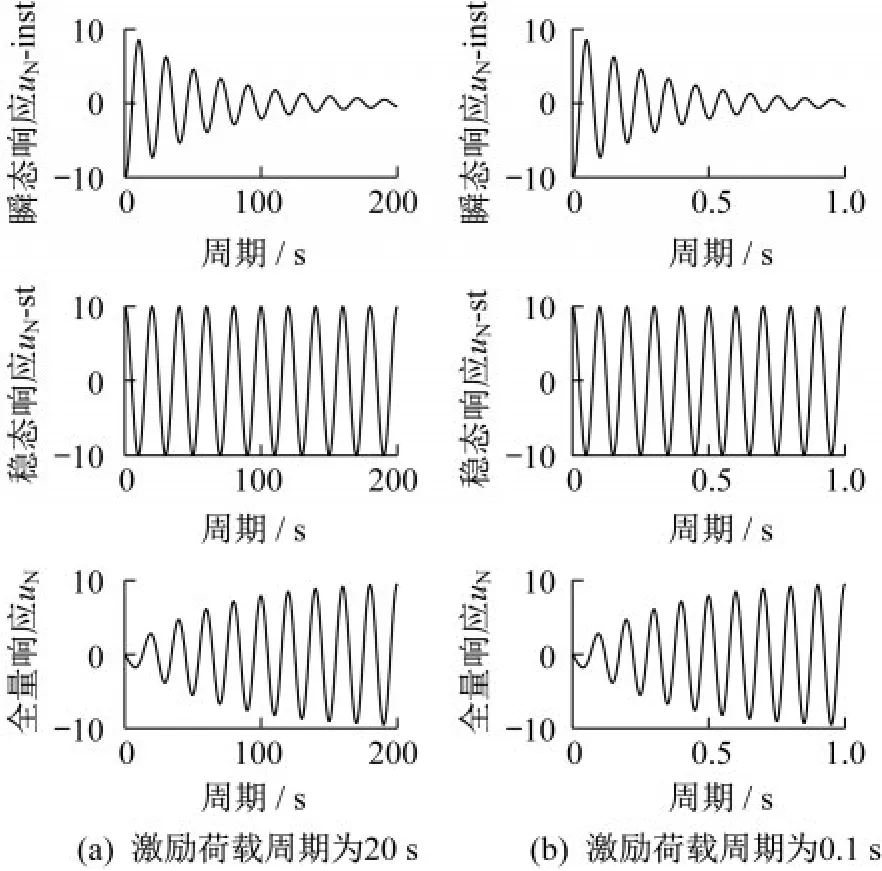
图1 标准化位移时程响应(β=1,ξ=0.05,P=10)Fig.1 Normalized displacement time history
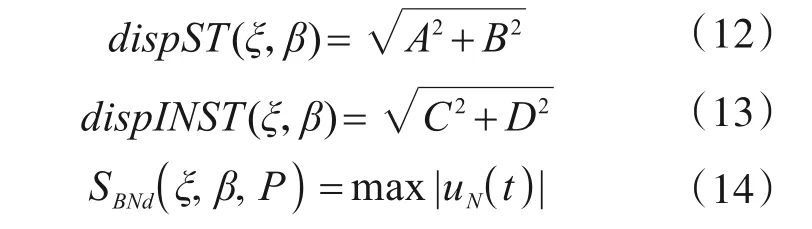
式 中 :dispST(ξ,β) 为位移稳态响应幅值;dispINST(ξ,β)为位移瞬态响应幅值;SBNd(ξ,β,P)为双规准位移反应谱;P为加载周数。符号中,disp代表位移,ST代表stable稳态响应,INST代表instante瞬态响应,N代表normal规准(规一化),BN代表binormal双规准。
1.3 真伪反应谱的关系
1.3.1 真伪绝对加速度谱的关系
将式(2)代入式(5)并与真谱式(4)对比,当ξ较小时,真谱与伪谱近似相等,当ξ=0时,真伪加速度积分公式相同,这也是“伪”谱命名的出发点。
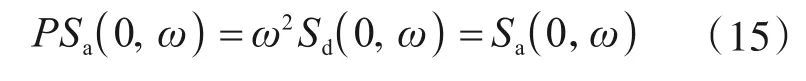
伪绝对加速度规准谱可以根据定义式(5)直接求得,其稳态幅值和瞬态响应幅值如下式所示:
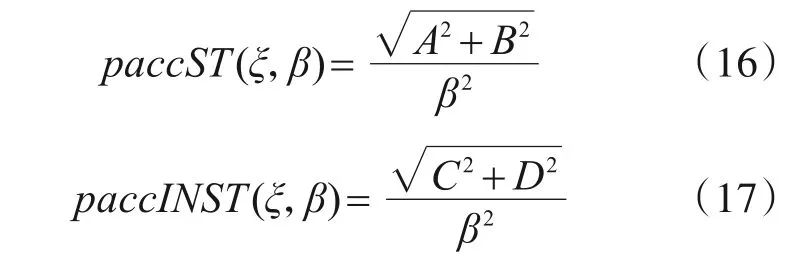
式中,paccST(ξ,β)为伪绝对加速度稳态幅值和paccINST(ξ,β)为伪绝对加速度瞬态响应幅值。符号中acc代表acceleration加速度,p伪、ST稳态、INST瞬态定义与前文相同。
故伪加速度谱与位移谱相差频率比β2倍,当β=1时,伪加速度谱与位移谱规准谱值相同即放大系数相同。
由运动方程可知质量乘以真加速度的惯性力反映的是弹性力式(19)与阻尼力式(20)的合力,而由式(20)可知当周期较长阻尼较大时,阻尼力与弹性力的比值变大。由于弹性力与阻尼力相位差为90度,合力可以表达为式(21),对该式作图2,当阻尼比为0时,惯性力与弹性力相等,即真加速度反应谱与伪加速度反应谱完全相同,真加速度谱的放大倍数随阻尼比增加和频率比增加而增加。长周期结构的响应以频率比为1的共振响应为主,但是也包含加速度谱峰值频率下的强迫振动当阻尼比取19%,频率比为1时,真加速谱比伪加速度谱大6%。当阻尼比取19%,频率比为10时,真加速谱比伪加速度谱大395%。

图2 真加速度谱与伪加速度的比值与频率比和阻尼比的关系图Fig.2 Relationship between the ratio of true acceleration spectrum to pseudo acceleration,frequency ratio and damping ratio
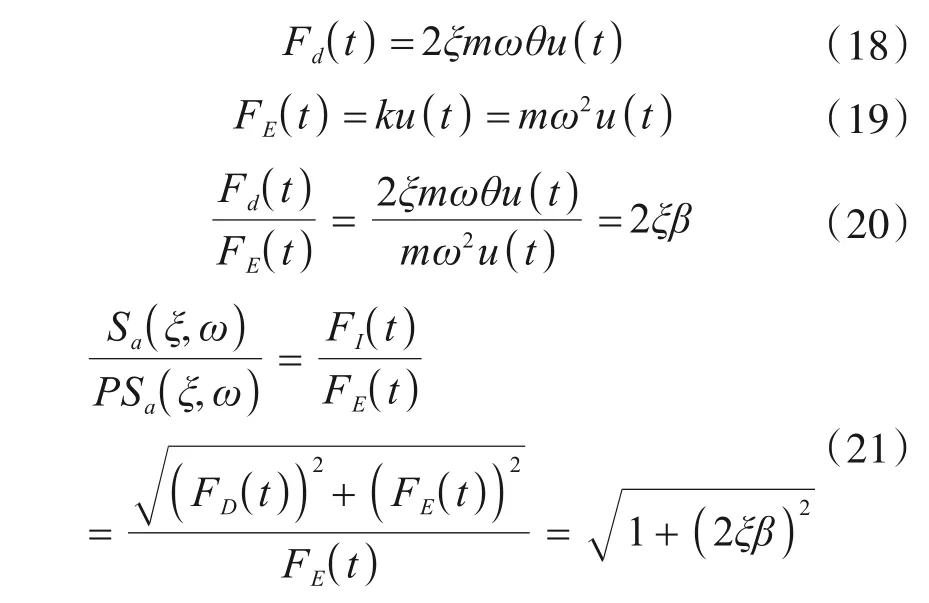
式中:FI是惯性力;FE是弹性力;Fd是阻尼力。
1.3.2 真伪相对速度谱的关系
伪相对速度规准谱可以根据定义式(6)直接求得,其稳态幅值和瞬态响应幅值如下式所示:
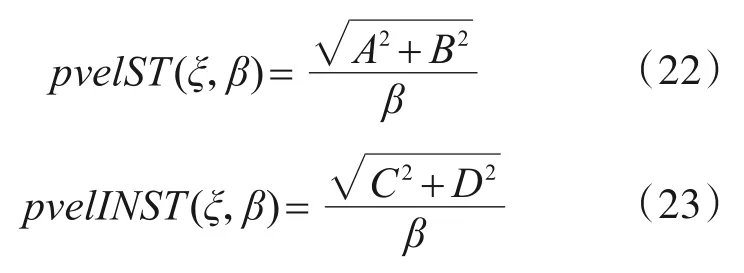
式中,pvelST(ξ,ω)为伪相对速度稳态幅值和pvelINST(ξ,ω)为伪相对速度瞬态响应幅值。符号中vel代表velocity速度,p伪、ST稳态、INST瞬态定义与前文相同。
故伪速度谱与位移谱相差频率比β倍,当β=1时,伪速度谱与位移谱规准谱值相同即放大系数相同。
相对速度标准时程可以由位移时程对时间求导,如下式所示:

当ξ=0时,式(24)稳态响应第二项可以约去,可以求出稳态响应的幅值velST(ξ,ω)和瞬态响应幅值velINST(ξ,ω)如式(25)、式(26)所示。
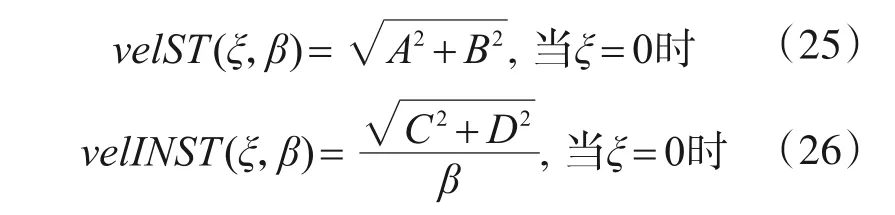
式中,velST(ξ,β)为真相对速度稳态响应的幅值和velINST(ξ,,β)为真相对速度瞬态响应幅值。符号中vel速度、p伪、ST稳态、INST瞬态定义与前文相同。
对比式(22)和式(25)及式(23)和式(26),真伪谱的瞬态响应幅值相同,当ξ=0时稳态响应幅值相差β倍,当β=1即共振时,稳态响应幅值也相同。所以,当ξ=0时,β=1时,真伪速度谱完全相同,如下图3所示。由上述分析可知,当结构位于速度敏感区时,即加载速度信号频率比约为1的范围内,真伪速度谱近似相等。
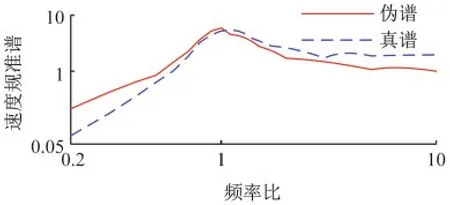
图3 真伪速度谱对比(ξ=0.01,P=2)Fig.3 Comparison of true and false velocity spectra
2 简谐荷载双规准反应谱的特征
分别采用突然加载和缓慢加载进行反应谱分析,简谐荷载双规准反应谱具有如下特点。
2.1 结构初始状态对于反应谱形状的影响
2.1.1 零初始相对速度对低频系统的影响
对简谐振动双规准位移反应谱随作图4(a),频率比大于2以后,结构响应随频率比即结构周期增加而增加,且加载周数越多,响应越大。值得注意的是结构响应随频率比增加很容易超过共振区,即误差很容易超过100%,显然这与实际地震响应不符。
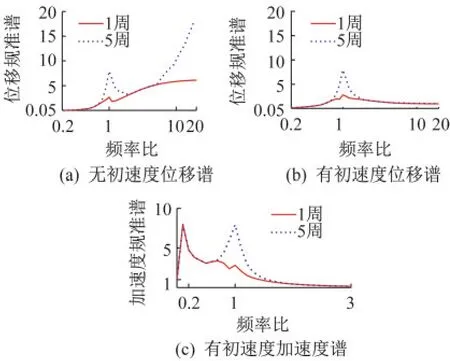
图4 初速度对反应谱影响(ξ=0.05)Fig.4 The influence of initial velocity on response spectrum
这是由于当加载频率比较大时,结构较柔,加载时质点绝对响应很小,相对位移以地面位移为主。可知,当结构无限柔时,相对位移等于地面位移。而对于初始速度和位移均为0的地面简谐加速度时程,积分后地面位移为式(27),式中存在时间一次项,导致地面位移随时间增加线性增加,出现基线漂移,显然与实际地震加载过程不符。
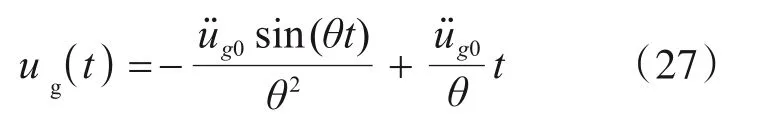
式中,ug(t)为地面位移时程。
2.1.2 非零初始相对速度对高频系统的影响
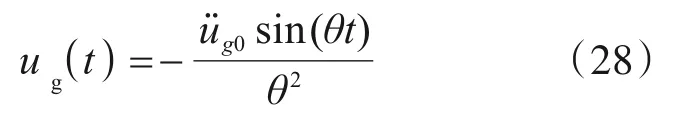
此时公式(11)原系数D将变为下式。
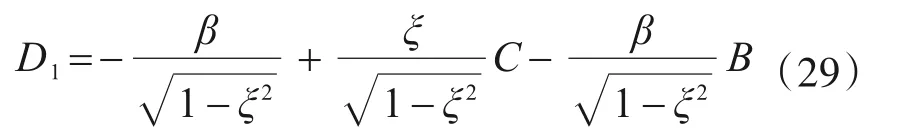
但是如图4(c)所示,加速度规准化反应谱在频率比较小时,即结构较刚时发生异常,当频率比为0.1时峰值与共振峰接近,误差达到100%,与实际地震动不符。这主要是由于,由于结构绝对初速度为0,故结构相对初速度与地面运动初速度大小相同方向相反为。当结构很刚时,质点本应紧跟地面随动,相对位移和速度将接近0,绝对加速度接近于地面加速度,即规准谱起点为1。但是对结构施加非0相对初速度将使其发生相对位移,由于高频结构刚度极大,导致结构内力很大,伪加速度谱反映了结构内力,使其失真,双规准谱远大于1。
2.2 模拟实际地震动的简谐作用加载方式
鉴于以上两种加载方式均与实际地震动不符,本文提出的加载过程试图模拟真实地震动过程中某一简谐分量的施加方式。真实地震过程中,地面运动某一简谐分量初位移、速度和加速度均为0,假设地面运动也是单自由度振子模型,地面受振源方向荷载激励并逐渐达到稳态峰值,由瞬态和稳态成分构成。本文选取与震源共振的信号进行研究,此时地面运动加速度信号为共振响应,共振响应[11]将如下式所示。
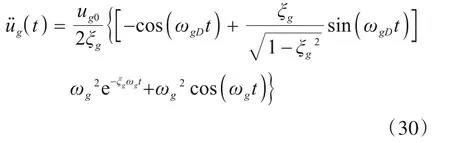
假设地面位移为ug0,ωg=4π,如图5所示,当地面阻尼比小时,以0.05为例,地面信号需在多周后达到峰值,模拟缓慢加载。当地面阻尼高时,以0.90为例,地面信号迅速到达峰值,模拟突然加载。
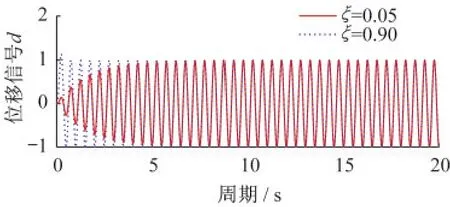
图5 位移时程响应与的比值(ωg=4π)Fig.5 The ratio of displacement time history to the
2.3 加载周数及缓慢加载与突然加载的关系
如图6所示,当加载过程持续40周时,即结构较为充分地进入稳态振动时,突然加载和缓慢加载的双规准反应谱峰值基本相同,但是冲击分量的存在导致突加荷载反应谱峰值段更宽,即上升和下降段更缓。
当加载周数较少时,即结构未充分进入稳态振动时,缓慢加载前若干周荷载作用幅值小于荷载稳态幅值,缓慢加载的放大系数幅值相比于突加荷载更小。
除此以外突然加载和缓慢加载谱线随频率比变化规律相近,故以下分析以突然加载为例分析。
2.4 反应谱峰值与阻尼比的关系
由公式(30)及图6可知,共振时结构需要往复多周后才能达到共振峰值。故加载周数较多时,结构可以达到共振峰值,瞬态荷载及其响应此时衰减充分。突加荷载和缓慢加载反应谱峰值一致,峰值均为,如图7所示。
2.5 反应谱峰值频率比与加载周数的关系
如图8所示,随加载周数减少,位移谱峰值频率比逐渐大于1,加速度峰值频率比逐渐小于1。反映了所叠加的瞬态荷载傅里叶幅值谱频率成分不单一且具有连续性的特征。地震地面运动加速度时程可以通过傅里叶变换为频域幅值谱F(ω),则同一地面运动的速度和位移频域幅值谱分别为F(ω)/ω和F(ω)/ω2,当幅值谱具有连续性时,加速度幅值谱的峰值频率更高,而位移幅值谱的峰值频率更低。
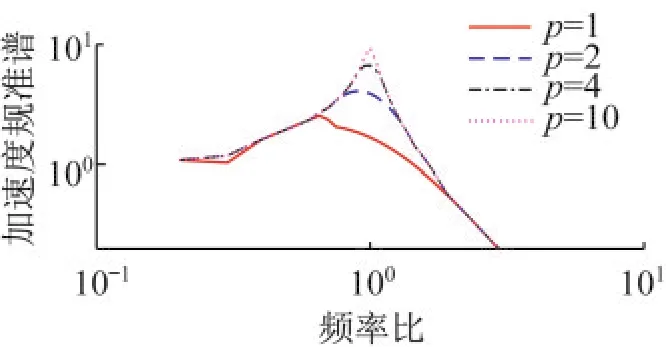
图8 不同加载周数双规准谱(ξ=0.05)Fig.8 Bi-Normalized spectrum with different loading cycles(ξ=0.05)
2.6 阻尼折减系数与加载周数的关系
随加载周数减少,阻尼比对峰值响应的折减作用减小。由于振动充分时,共振响应受阻尼比影响较大,而当加载周数较少时,瞬态响应衰减不充分,响应未攀升至稳态共振峰值,瞬态响应主要受结构初始状态影响和加载速度荷载影响,受阻尼比影响不大。对不同加载周数简谐荷载的阻尼比折减系数分析结果作图9能够体现该规律,即等间距阻尼比下结构峰值响应的间距随加载周数的增加而增加。
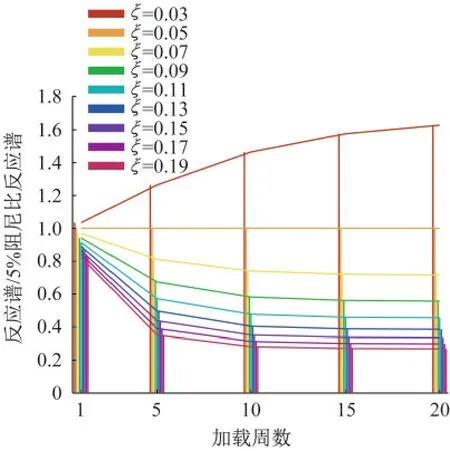
图9 阻尼折减系数随加载周数变化条形图Fig.9 Damping reduction factors vary along with loading cycles
3 设计反应谱特征及影响因素
3.1 设计反应谱的基本特征
设计谱与单一地震波反应谱不同,体现了该场地可能发生的所有地震信号在各敏感段内的统计特征。
3.1.1 设计反应谱在各谱敏感段内出现平直段
根据前述分析,地面位移对低频段敏感,速度对中频段敏感,加速度对高频段敏感。当震源类型、震级、震中距、场地类别相同时,可以认为一组地震信号除地面运动信号峰值相近外,持时、特征周期、加载速度等特性相近。由双规准谱分析可知,峰值放大系数仅与加载周数和加载速度相关,故在各敏感段内一组信号的峰值放大系数接近。如图10所示,设计反应谱作为统计谱将在各谱敏感段内表现为平直段。
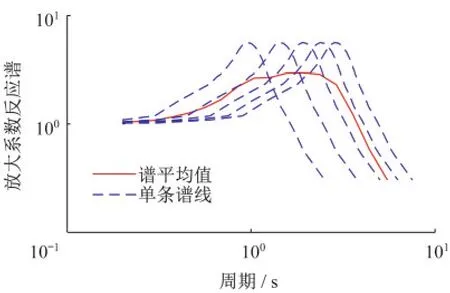
图10 不同加载频率下简谐加载加速度谱及谱平均值(P=3,ξ=0.05)Fig.10 Acceleration spectrum and spectral mean value of harmonic loading at different frequencies
3.1.2 建议的反应谱曲线表达式
根据上述分析,建议我国规范采用Newmark[10]提出的“伪加速度-速度-位移三联谱”,即将三种谱线的峰值响应统计值简化为平直段,且三个谱之间严格满足转换关系式(5)和式(6),未被三联谱平直段覆盖的周期取线性内插至理论极限值。
如图11所示,由于速度谱和位移谱与加速度谱之间存在式(5)和式(6)的转换关系,将它们转换为加速度谱时,速度谱平直段转换为一次曲线下降段,位移谱平直段转换为二次曲线下降段。所以,加速度谱除平直段外,两紧邻曲线下降段体现的也是结构与地震动输入的共振放大效应。相关公式如表1、表2所示。
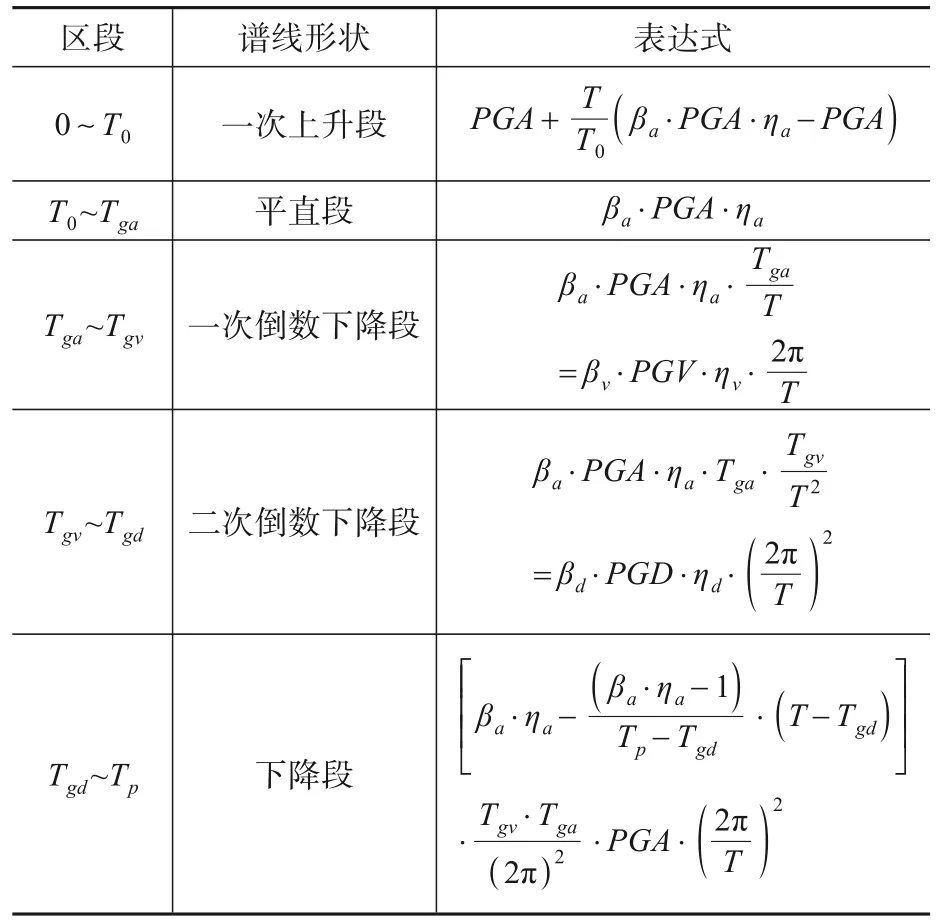
表2 伪加速度谱表达式Table 2 Pseudo acceleration spectrum expression
图11中,βa为加速度反应谱地面信号放大系数平台段取值,βv为速度反应谱地面信号放大系数平台段取值,βd为位移反应谱地面信号放大系数平台段取值,Tga为加速度平直段终点也是速度平直段起点,Tgv为速度平台终点也是位移平直段起点,T0为加速度谱平直段起点周期,Tgd为位移谱平直段终点周期,Tp为位移谱线性下降至理论极限的周期。
PGA为地面峰值加速度;PGV为地面峰值速度;PGD为地面峰值位移;η代表各阻尼比反应谱相比于5%阻尼比反应谱的阻尼折减系数。其余符号含义与图11符号含义相同。
3.1.3 加三敏感段峰值放大系数依次减小
由第2.3节分析可知,反应谱放大系数β将随加载周数即地震动持时与特征周期的比值增加而增加,且共振时三种谱的放大系数相同。故对同一地震事件的谱而言,由于持时相同,加速度谱、速度谱、位移谱的特征周期渐次增加,加载周数依次减小,所以β渐次减小。
3.1.4 转折点周期正比于右侧谱与左侧谱峰值比值
由于各谱平直段均可以转换为加速度谱,且加速度谱连续,可以根据分界点处的关系推导得出关系式(31)、式(32),即转折点周期与右侧谱与左侧谱峰值的比值成正比。
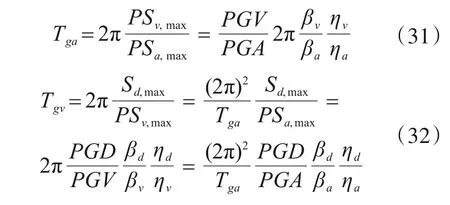
3.1.5 常见结构设计反应谱可由三参数标定
由于我国发改委2021年规定“严格限制建设500米以上超高层建筑”,根据徐培福等提出的结构周期与高度的经验公式[14],未来大部分建筑周期小于9 s。参考美国规范[15]反应谱参数6 s≤Tgv≤12 s,位移平直段结束周期Tgd一般大于10 s。所以,我国常见结构周期范围内加速度反应谱可以完全由三个参数标定。可由三联谱各谱峰值,即三平直段高度标定,如式(33)所示。也可以根据转折点周期与谱峰值的关系,由PSa,max、Tga、Tgv三个参数完全表达,如式(34),两者是等价的。
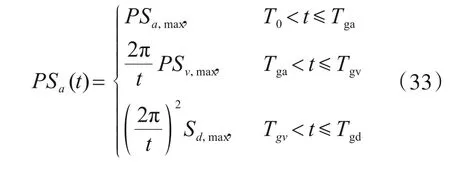
式中,t为反应谱横坐标结构周期。
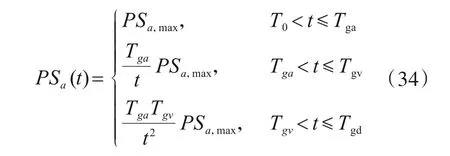
式中,PSa,max=βa·PGA·ηa为加速度反应谱平直段取值,PSv,max=βv·PGV·ηv为速度反应谱平直段取值Sd,max=βd·PGD·ηd为位移反应谱平直段取值。
3.2 阻尼对设计反应谱的影响
3.2.1 三敏感段阻尼折减系数间距依次减小
加速度、速度、位移平直段之间有显著差别,其中加速度谱不同阻尼比的谱曲线间距最宽,位移谱对应的间距最窄。这是由于三种谱的特征周期依次加长,对于同一地震作用,持时相同,反应谱周期越长,加载周数越少,如同一持时为50 s的地震波,假设加速度特征周期为1 s,位移特征周期为5 s,则加载周数分别为50周和10周。根据第1节分析可知,随加载周数减少瞬态响应占比逐渐加大,阻尼影响逐渐减小,即阻尼折减系数间距逐渐变小。
3.2.2 阻尼折减系数与具体周期无关
我国规范编制组认为阻尼折减系数应与周期相关。但是由前述分析可知加速度反应谱实际上体现的是加速度、速度和位移的共振响应,由简谐地震反应谱分析可知,共振峰值阻尼折减系数仅与加载周数、阻尼比、加载速度相关,对具体场地而言,震源类型、震级、震中距、场地类别相同,可以认为上述参数相同,所以某一平直段折减系数与具体周期无关。
3.2.3 随阻尼增加反应谱转折点周期逐渐右移
根据式(31)、式(32)特征周期可以由右侧谱与左侧谱峰值段比值表达,且阻尼比增加时右侧谱折减程度小于左侧,故特征周期随阻尼比增加逐渐右移。
3.3 地震动特性对设计反应谱的影响
场地的地震动频谱特性主要由震级、震中距和场地类确定。
3.3.1 烈度对于长周期反应谱的影响
从定性角度而言,由地震学的基本理论可知[16],震级越大,振源破裂面就越长,地震脉冲持时也会变长,故傅里叶变换后长周期分量增多。即烈度对于长周期位移敏感段特征周期影响显著。
从定量的角度而言。根据周锡元等[17]给出的拟合式(35),假设震中距R取定值时,则M每增大级时,设防烈度I提高1度。但根据里氏震级的定义式(36),此时地面运动位移幅值Amax将依次放大倍。同时,大震级时长周期分量更为丰富,持时更长,位移反应谱峰值放大系数也将进一步放大。所以如图12所示,若以6度反应谱为基准,8度下位移敏感段反应谱需至少放大16倍才能获得准确取值,根据式(31)、式(32)反应谱转折点周期也将显著右移。可见震级对反应谱位移敏感段影响显著。
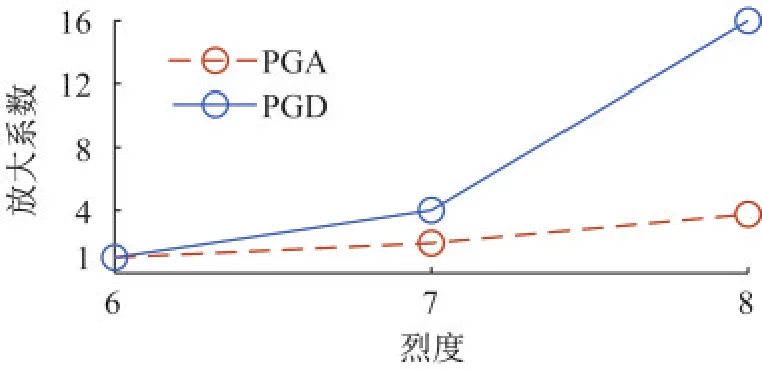
图12 地面峰值加速度和峰值位移随烈度增加的放大系数Fig.12 The amplification factor of PGA and PGD

式中:M为里氏震级;I为设防烈度;R为震中距;A0是距震中100 km处接收到的0级地震的地震波振幅;Amax是距震中100 km处接收到的所测量地震的地震波振幅,单位μm。
目前我国规范未考虑震级对特征周期的影响,显然低估了高烈度区长周期段反应谱取值,但采用斜直线下降段替代二次曲线下降段,并在6 s后拉平反应谱来提高地震作用,一定程度上对这种低估进行了弥补[18]。但必须指出,这种简化方法是基于长周期信号数量少精度低的情形提出的[8],随着宽频采集仪等采集设备的进步和地震事件的积累,有条件适时提高我国反应谱的精度,替换简化方法。
3.3.2 震中距对于场地设防地震参数的影响
由于同一地震事件不同震中距的长周期分量丰富程度不同,震中距增加时长周期分量衰减慢而短周期分量衰减快[20]。如图13所示,考察位移敏感段的反应谱高度,很可能出现加速度谱峰值较大的近震小于加速度谱峰值较小的远震的情况。目前我国规范以加速度谱平直段的高度标定烈度,对于短周期结构有明确的设计指导作用,但对于中长期结构,加速度平台高的情形不一定是最不利情形。建议非单一震源地震区,分别给出使加速度、速度和位移平直段最高的三组参数,或给出包络参数,以使各周期段的结构设计均安全可靠。
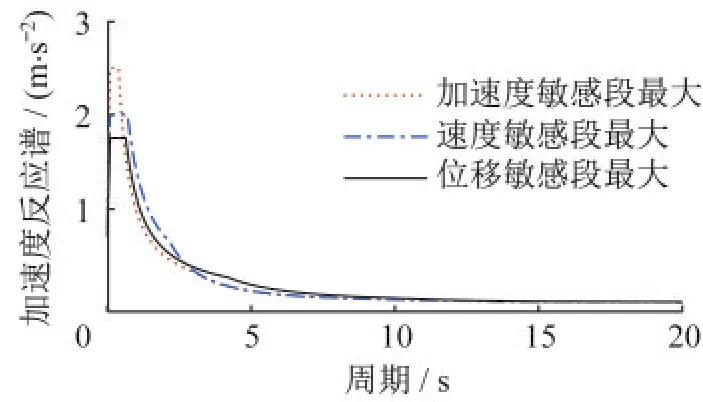
图13 加速度、速度和位移敏感段分别最大的三种情形Fig.13 The three cases with the highest acceleration,velocity and displacement respectively
4 结论和建议
本文对真伪反应谱的物理意义进行了分析,并利用简谐荷载双规准谱分析了地震反应谱的一般规律。提出以下结论和建议:
(1)简谐波加载与地震真实加载过程不符,会导致反应谱失真。真实加载过程应考虑加载速度的影响。影响简谐荷载双规准反应谱的因素主要包括加载周数、阻尼比、加载速度、频率比。
(2)建议规范修订设计加速度反应谱为伪加速度反应谱或三联谱,并利用宽频强震记录仪充实我国低频长周期强震记录波库,标定反应谱参数。加速度谱、速度谱、位移谱可以互相转换,即三者任一反应谱均能完整表达结构在各敏感周期范围内的响应。
(3)在常见结构的周期范围内,反应谱可以由三个参数完全标定和表达,即三联谱三个平直段高度,或伪加速度谱平直段高度及分别进入速度敏感段和位移敏感度段的转折点周期Tga和Tgv。建议规范将全国各地设防烈度和地震分组两参数表改为各地标准场地三参数表。若仍采用地震分组即震中距和衰减关系标定周期转折点参数,建议补充周期转折点与震级或设防烈度的关系。
(4)所建议的反应谱随阻尼增加不存在“反超现象”。阻尼折减系数与具体周期无关。阻尼增加时,周期转折点右侧受阻尼影响小于左侧,转折点周期右移。建议标定三个敏感平直段的阻尼折减系数,以更符合实际地震动特性。
(5)设防烈度对于长周期反应谱或转折点周期取值有显著影响。建议采用转折点周期延长的方式取代斜直线下降段和6 s后拉平规定,以合理地反映烈度对反应谱的影响。
(6)建议对任意场地分别给出使各敏感段最不利的三组反应谱参数或一组包络参数。

