基于mRMR和MA-RELM的火电厂出口SO2质量浓度预测

金秀章， 刘 岳， 赵文杰， 于 静

(华北电力大学 控制与计算机工程学院，河北保定 071003)

随着我国对环境保护问题的日益重视，降低燃煤电厂出口SO2排放量是当前所有电力企业面临的重要问题[1]。目前，火电厂主要采用的烟气脱硫方式为石灰石-石膏湿法脱硫，该方法具有成本低、脱硫效率高等优点，但存在系统惯性迟延大、实时性较差和难以控制等缺点。建立准确的出口SO2质量浓度预测模型可以提前预测出口SO2质量浓度的变化，便于运行人员及时调整供浆量，从而实现SO2的超低排放[2]。

基于数据驱动的建模被广泛应用于SO2质量浓度预测。苏翔鹏等[3]通过径向基函数(RBF)神经网络建立了脱硫系统出口SO2质量浓度预测模型。王琦等[4]利用支持向量机(SVM)建立了出口SO2排放预测模型。由于浅层神经网络无法深入挖掘数据中的特征信息，而深度神经网络(DNN)具有强大的非线性映射能力和特征提取能力，近年来被广泛应用于数据驱动建模预测中。唐振浩等[5]利用DNN建立了NOx排放量预测模型。刘亚珲等[6]利用卷积神经网络(CNN)进行特征提取，通过长短期记忆网络(LSTM)对电力负荷进行预测，预测效果较好。虽然采用DNN可以提高模型的预测精度，但存在使用成本高、训练时间长和调参困难等缺点。极限学习机(ELM)是一种新型神经网络，具有训练参数少、学习速度快和泛化能力强等优点。张淑清等[7]利用ELM建立了电网负荷的预测模型，并通过飞蛾火焰优化算法对模型参数进行优化。He等[8]利用核极限学习机(KELM)对煤质含量进行预测分析，并将其与其他模型进行对比，验证了KELM的有效性。

模型的特征选择也是影响其预测精度的重要因素。特征选择方法主要分为过滤法、包装法和嵌入法3种。过滤法是利用输入变量与输出变量之间的相关性来筛选特征变量，包括互信息(MI)算法[9]、最大相关最小冗余(mRMR)算法[10]和相关特征选择(CFS)[11]等。包装法是通过将各特征子集输入到预测模型中进行预测，并将预测误差作为评价指标。嵌入法是将特征变量输入到某机器学习模型中，通过训练得到各特征的权值系数，其通过权值系数来筛选特征变量。常用的嵌入法包括套索算法(LASSO)[12]和基于随机森林[13]的特征选择算法等。

笔者提出了一种基于mRMR特征选择和蜉蝣算法优化正则化极限学习机(MA-RELM)的出口SO2质量浓度预测方法，将其与经典优化算法粒子群算法(PSO)[14]、灰狼优化算法(GWO)[15]的寻优结果进行比较，并分别利用正则化极限学习机(RELM)、ELM、最小二乘支持向量机(LSSVM)和LSTM对最优特征子集进行训练和测试，以证明RELM在预测精度和训练时间上的优越性。

1 基本原理

1.1 互信息和mRMR算法

互信息是信息论中用于评价变量之间相互依赖程度的度量，既能反映两组变量间的线性相关性，又能反映非线性相关性。对于2组离散型随机变量X和Y，两者之间的互信息I(X;Y)为：

(1)

式中：p(x)和p(y)分别为X和Y的边缘概率分布函数；p(x,y)为X和Y的联合概率分布函数。

如果随机变量X中共包含n个数据，分别为(x1,x2,…,xn)，将数据平均划分为n段，统计各个数据在不同范围的数据段里出现的个数，将统计好的个数除以n作为不同数据段的概率分布，即为X的边缘概率分布函数。

(2)

Xmax=Xmin+(n-1)×Δ

(3)

式中：Xmax为最大值；Xmin为最小值；Δ为平均值。

联合概率分布函数的计算方法与边缘概率分布函数类似，但由于涉及到2组随机变量，因此组成的是有限大小的二维平面。将该平面划分为n×n个小正方形模块，通过计算X和Y中各坐标点落入不同模块的数量，从而得到关于X与Y的联合概率分布函数。

mRMR算法不仅考虑了输入变量与输出变量之间的相关性，还考虑了各输入变量间的相关性，通过mRMR算法可以从初始输入变量中找到与输出变量相关性最大、与输入变量间相关性最小的特征子集。

(4)

式中：Sn为输入变量特征集合；Z为输出变量；Xi为待选输入变量；Xj为已选输入变量。

由于特征子集的组合方式过多，因此采用增量搜索的方式[16]来依次挑选最优特征子集，最优特征子集满足如下公式：

(5)

式中：m为特征子集中的已选变量个数。

1.2 RELM

ELM是一种改进的单层前馈神经网络(SLFN)，由输入层、隐藏层和输出层组成。其中，输入层与隐藏层之间是全连接，隐藏层输出H(s)为：

H(s)=[h1(s)h2(s) …hL(s)]

(6)

hi(s)=g(wis+bi)

(7)

式中：hi(s)为第i个隐藏层节点的输出，i=1,2,…,L，其中L为隐藏层神经元个数；s为输入变量;g()为激活函数，常见的激活函数有Sigmoid函数、Gaussian函数等；wi和bi分别为隐藏层节点上的权值和偏差。

ELM输出层的公式为：

(8)

式中：β为隐藏层节点与输出层节点之间的输出权重，β=[β1β2…βN]；βj为第j个输出层节点上的输出权重；N为输出层神经元个数；fL(s)为输入变量为s时对应的ELM输出值。

ELM的训练过程实际上就是对wi、bi和β这3个未知量的求解过程。在ELM中，隐藏层节点参数wi和bi根据任意连续的概率分布随机生成，由于两者并不是经过训练确定的，因此ELM较传统神经网络具有更高的效率。

输出权重β主要通过最小化训练误差的方法进行求解，其目标函数为：

(9)

式中：H为隐藏层的输出矩阵；T为训练数据的目标矩阵。

RELM是在原目标函数的基础上引入了L2正则化项[17]，通过正则化以防止模型过拟合，提高了ELM的泛化能力，改进后的目标函数为：

(10)

式中：C为正则化因子。

1.3 蜉蝣算法(MA)

MA[18]是一种新的群智能优化算法，其灵感主要来自于自然界蜉蝣的飞行行为和交配行为。由于该算法独特的求偶行为和交配机制，相比于其他群体智能算法，该算法在收敛精度和收敛速度方面都具有一定的优势。

首先，随机产生2组蜉蝣，分别代表雄性和雌性种群，根据适应度函数f(x)对每个蜉蝣个体进行评价。其中，雄性蜉蝣成群聚集，每只雄性蜉蝣的位置更新与相邻蜉蝣有关。设xi,t为t时刻时雄性蜉蝣i的位置，则其位置更新公式如下：

xi,t+1=xi,t+vi,t+1

(11)

式中：vi,t+1为t+1时刻蜉蝣i的速度。

(12)

式中：vi,j,t+1为蜉蝣个体i在j维度时t+1时刻的速度；xi,j,t为雄性蜉蝣个体i在j维度时t时刻的位置；a1和a2为社会作用正吸引系数；pbest,i,j为当前蜉蝣个体i在j维度历次迭代中的历史最佳位置；gbest,j为种群中所有蜉蝣在j维度的最佳位置；δ为能见度系数；rp为雄性蜉蝣当前位置与历史最佳位置的距离；rg为雄性蜉蝣当前位置与种群最佳位置的距离。

通过聚集行为，雄性蜉蝣种群之间加强了不同个体间的信息共享与合作，从而提高了搜索空间的效率，加快了收敛速度。

由于群内最好的雄性蜉蝣还会上下舞蹈，因此其速度不断改变。这种独有的舞蹈行为为算法引入了随机元素，可以有效防止算法陷入局部最优。

vi,j,t+1=vi,j,t+d×r

(13)

式中：d为舞蹈系数；r为[-1,1]之间的随机数。

与雄性蜉蝣不同，雌性蜉蝣不会成群聚集，而是会飞向雄性蜉蝣。假设yi,t为t时刻雌性蜉蝣i的位置，则其位置更新公式如下：

yi,t+1=yi,t+vi,t+1

(14)

蜉蝣的速度更新公式如下：

vi,j,t+1=

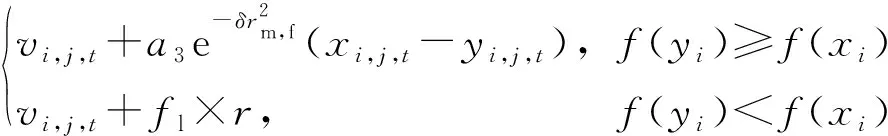
(15)

式中：rm,f为雌性蜉蝣与雄性蜉蝣的距离；fl为随机游走系数;a3为社会作用正吸引系数;yi,j,t为雌性蜉蝣个体i在j维度时t时刻的位置。

蜉蝣的交配过程是从2个种群中各选择1个亲本，选择可以随机，也可以基于其适应度函数，即最好的雌性与最好的雄性繁殖，次好的雌性与次好的雄性繁殖。通过交配产生2个新的个体可行解j1和j2，其更新公式如下：

(16)

式中：ω1为蜉蝣父本可行解；ω2为蜉蝣母本可行解；k为特定范围的随机数。

这种交叉进化的方式在逐步淘汰适应度较差个体的同时还可以防止算法陷入局部最优，提高了MA的收敛精度。蜉蝣算法的流程如图1所示。

图1 蜉蝣算法流程图Fig.1 Mayfly algorithm flow chart

2 出口SO2质量浓度预测模型

2.1 基于互信息的时延分析

在建立出口SO2质量浓度预测模型时首先确定模型的输入变量，通过机理分析法，从采集的输入变量中筛选出与出口SO2质量浓度相关的8个输入变量，见表1。

表1 输入变量的范围Tab.1 Range of input variables

由于燃煤机组和脱硫系统都是具有大迟延、大惯性的系统，因此选取的相关变量与出口SO2质量浓度之间存在一定的时延。为保证输入变量与输出变量在时序上保持一致，对输入变量进行特征选择前先对其进行时延分析。常用的时延分析方法为滑动窗口法，即保持输出变量不变，计算输入变量前ns内各个时刻与输出变量的相关性，取相关性最大时对应的时间作为该输入变量与输出变量之间的时延[5]。由于锅炉燃烧和烟气脱硫过程最大不超过600 s，故n取值为600。

笔者在传统时延计算方法的基础上进行了改进，首先利用互信息代替person相关系数来计算输入变量与输出变量间的相关性，再利用电厂不同工况下的数据对同一变量进行时延分析，通过综合不同工况下的结果来确定最终的时延。虽然工况发生变化时输入变量与输出变量间的时延可能会小幅变化，但也从侧面验证了分析结果的准确性。通过改进的时延分析方法确定的各输入变量的时延和最大互信息见表2。

表2 输入变量与输出变量间的时延及最大互信息 Tab.2 Time delay and maximum mutual information between input variables and output variables

2.2 基于mRMR算法的特征选择

笔者在所选输入变量的基础上加入了2个新的输入变量，即脱硫塔液气比和钙硫比。其中，液气比是指吸收1 L烟气所需的浆液量，钙硫比是指脱硫消耗的吸收剂CaCO3与脱除的SO2之间的物质的量比。由于液气比和钙硫比能够具体反映脱硫塔内部脱硫反应的变化情况，因此在已选输入变量的基础上，通过近似计算得到液气比和钙硫比。将这2个新增输入变量与上述8个输入变量共同组成初始输入变量，并通过特征选择来去除冗余变量，从而简化模型结构，提高模型的训练速度和泛化能力。

利用mRMR算法对初始输入变量进行特征选择，首先通过增量式搜索确定各初始输入变量依次加入到特征子集的顺序为入口烟气体积流量、石灰石浆液供浆体积流量、钙硫比、入口SO2质量浓度、液气比、机组负荷、锅炉总风量、石灰石浆液密度、脱硫塔pH值和脱硫塔液位。传统mRMR算法是根据特征子集相关性之和来确定最优特征集，并没有考虑到特征子集与预测模型之间的相互作用。笔者设计了一种将mRMR算法与MA-RELM预测模型相结合的特征选择算法，即将mRMR算法排序后的特征子集分别输入到RELM预测模型中，利用MA对RELM预测模型参数进行优化，并将最后的寻优结果作为该特征子集的评价函数。利用改进mRMR算法得到各个特征子集，从而建立不同的RELM预测模型，其预测结果见表3。从表3可以看出，当特征子集取特征数为9时，RELM预测模型的预测误差最低，此时隐藏层神经元个数为16，正则化因子为20.700 4。

表3 不同特征子集下RELM预测模型的预测结果和模型参数Tab.3 Prediction results and model parameters of the RELM prediction model under different feature subsets

2.3 MA-RELM预测模型

利用MA对RELM预测模型参数进行优化，即为MA-RELM预测模型。由于MA的参数较多，因此通过多次实验确定相关参数如下：社会作用正吸引系数a1和a2均为1.5，能见度系数δ为2，舞蹈系数d为0.8，随机游走系数fl为1，L和r均为[-1,1]范围内的随机数，种群数量设置为30，迭代次数设为3 000。通过多次迭代确定模型的最优隐藏层神经元个数和正则化因子。由文献[19]可知，在隐藏层神经元个数和正则化因子确定的情况下对ELM的隐藏层节点参数进行优化可以进一步提高模型的预测精度。表4为不同隐藏层神经元个数和正则化因子下隐藏层节点参数寻优前、后的模型预测结果，其中λRMSE为均方根误差。从表4可以看出，在确定隐藏层神经元个数和正则化因子后，通过对隐藏层节点参数进行优化可以进一步提高模型的预测精度。

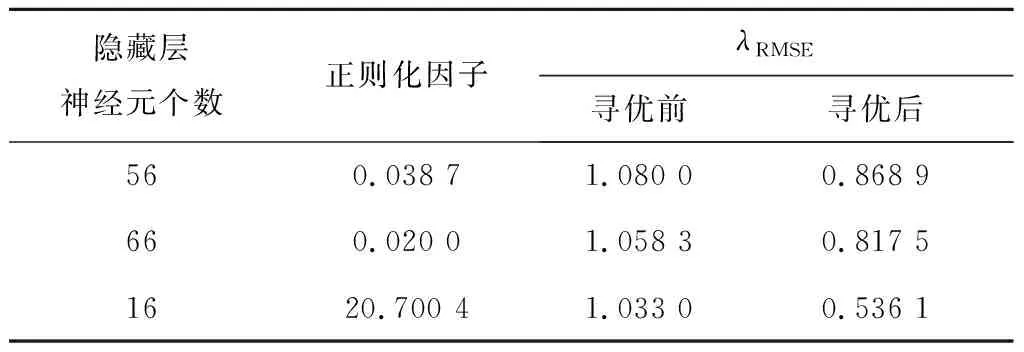
表4 隐藏层节点参数寻优前、后的预测结果Tab.4 Prediction results before and after optimization of hidden layer node parameters

3 结果与分析

3.1 实验设计与模型评价指标

为验证MA-RELM预测模型的有效性，利用山西某600 MW燃煤电厂提供的数据进行预测实验。该电厂采用石灰石-石膏湿法进行脱硫。通过对数据进行筛选，最终选出2 500组代表性数据，其中2 000组作为训练集，500组作为测试集，采样周期为10 s。此外，将数据输入到RELM预测模型时需进行归一化处理，避免各个输入变量因量级不同而对预测结果产生影响，同时可缩短模型的训练时间。

采用的模型评价指标为λRMSE、平均相对误差λMAPE和皮尔逊相关系数R。

(17)

(18)

(19)

3.2 实验结果

3.2.1 不同预测模型对实验结果的影响

为体现RELM预测模型的优势，分别利用ELM、LSTM和LSSVM搭建了预测模型，并利用MA确定了ELM和LSSVM的模型参数，由于LSTM单次训练时间较长，难以通过MA确定模型参数，因此采用网格搜索算法确定参数。4种预测模型的出口SO2质量浓度预测结果以及评价指标分别见图2和表5。从图2和表5可以看出，4种预测模型的出口SO2质量浓度变化趋势均接近于真实值，但与LSTM、LSSVM和ELM相比，RELM的λRMSE分别降低了38%、36%和26%，λMAPE分别降低了35%、38%和28%。结果表明，与LSSVM和LSTM相比，RELM具有更强的预测拟合能力；与ELM相比，RELM由于加入了正则化项，其泛化能力提高，因此预测误差进一步降低。

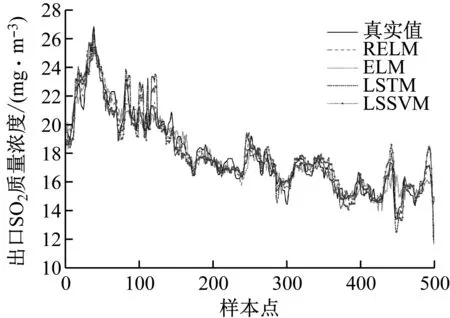
图2 不同预测模型下的出口SO2质量浓度预测结果Fig.2 Prediction results of outlet SO2 mass concentration under different prediction models

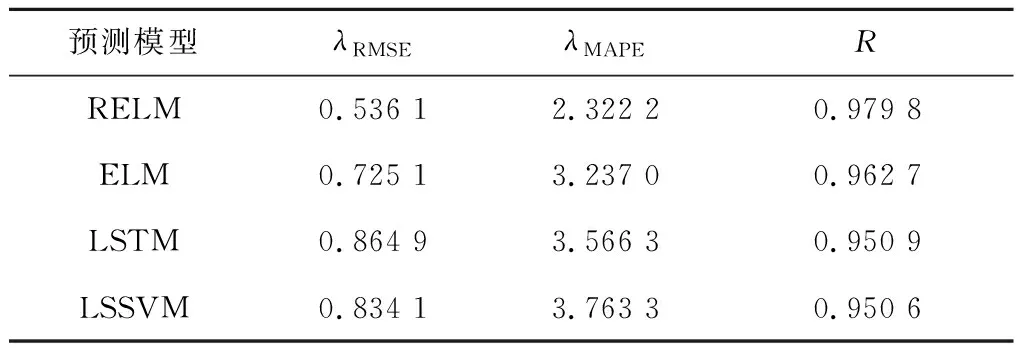
表5 不同预测模型的评价指标Tab.5 Evaluation indexes of different prediction models

3.2.2 不同优化算法对实验结果的影响

笔者采用了MA对RELM预测模型参数进行优化。为体现其优点，选取PSO和GWO作为对比寻优算法，在采用相同特征子集、种群个数和迭代次数的前提下，分别对RELM预测模型的隐藏层神经元个数、正则化因子和隐藏层节点参数进行多次寻优。不同优化算法的评价指标见表6。

表6 不同优化算法的预测结果Tab.6 Prediction results under different optimization algorithms

不同优化算法下出口SO2质量浓度预测结果见图3。由图3可知，相比于PSO和GWO，MA具有更高的收敛精度，由于其特有的随机舞蹈和雌雄种群交配机制，既避免了算法陷入局部最优，又能够在群体内交换经验，使算法快速收敛。采用MA对模型参数进行优化可以进一步降低模型的预测误差。

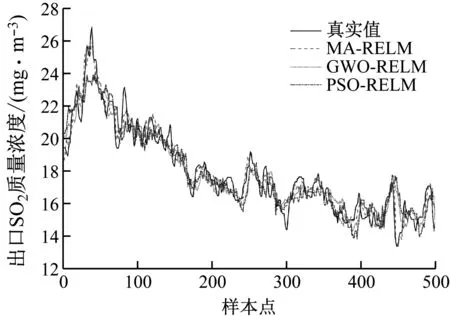
图3 不同优化算法下出口SO2质量浓度预测结果Fig.3 Prediction results of outlet SO2 mass concentration under different optimization algorithms

3.2.3 时延分析对实验结果的影响

时延分析前、后MA-RELM预测模型得到的出口SO2质量浓度预测结果以及评价指标分别见图4和表7。与时延分析前相比，时延分析后MA-RELM预测模型的λRMSE降低了11%，λMAPE降低了12%。由此可见，对输入变量的数据进行时延补偿可以提高预测模型的精度。

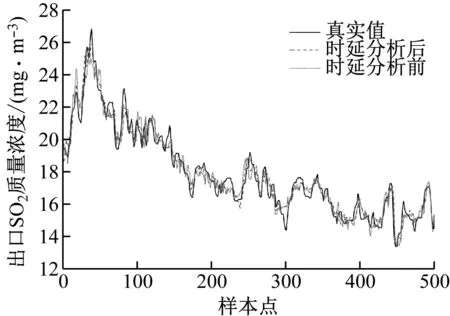
图4 时延分析前、后出口SO2质量浓度预测结果Fig.4 Prediction results of outlet SO2 mass concentration before and after time delay analysis

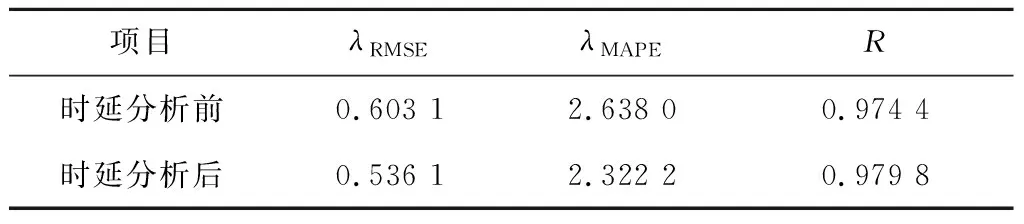
表7 时延分析前、后MA-RELM预测模型的评价指标Tab.7 Evaluation index of MA-RELM prediction model before and after time delay analysis

4 结 论

(1) 与LSSVM和LSTM相比，RELM具有更高的预测精度和更快的训练深度；与ELM相比，RELM通过加入正则化项可防止预测模型过拟合，泛化能力得到提高。

(2) 相比于PSO和GWO，MA具有更高的收敛精度，经MA优化后RELM预测模型的误差降低。

(3) 将mRMR算法与MA-RELM预测模型相结合实现了理论上最优特征子集的筛选。通过对输入变量进行时延分析可以提高输入变量与输出变量间的相关性，从而提高预测模型的预测精度。