T91/TP347H异种钢焊接接头高温拉伸性能研究

高 巍， 纪冬梅， 潘卫国， 刘川槐

(1. 上海电力大学 能源与机械工程学院， 上海 200090；2. 淮浙电力有限责任公司凤台发电分公司， 安徽淮南 232131)

马氏体耐热钢具有良好的高温抗氧化性能和高蠕变强度等特点，奥氏体钢蠕变断裂强度不如马氏体耐热钢，但奥氏体钢具有在温度升高的情况下，其蠕变断裂强度降低的速率远低于马氏体耐热钢的特点，两者被广泛应用于火力发电机组中[1]。随着火力发电机组向大容量、大参数方向发展，马氏体耐热钢和奥氏体钢组成的异种钢焊接接头得到了广泛应用，但由于2种钢材有着不同的物理化学性质，特别是二者的线膨胀系数不同，导致异种钢焊接接头成为管道失效的关键位置。国外学者对异种钢焊接接头的研究较少，而国内学者对异种钢焊接接头的研究方向主要集中在蠕变疲劳、裂纹扩展、氧化层和微观组织分析等[2-9]，关于异种钢拉伸性能和本构模型的研究几乎未见报道。此外，针对有限元模拟方面的研究也较少，并且主要集中在材料蠕变[10-12]、断裂[4, 13-14]和焊接过程[15-17]方面的模拟。

笔者以T91/TP347H异种钢焊接接头为研究对象，对接头及两端母材进行高温短时拉伸试验，基于试验数据，利用并改进双线性模型和多线性模型构建了该异种钢焊接接头和母材的高温拉伸本构模型，并基于高温拉伸本构模型模拟了T91/TP347H异种钢焊接接头的高温拉伸过程，同时对模拟结果进行讨论分析。

1 试验介绍

针对T91/TP347H异种钢焊接接头和两端母材开展不同加载速率下的高温拉伸试验。原始状态接头和两端母材由某锅炉厂提供，焊接接头的焊丝为ERNiCr-3，采用全弧焊焊接而成。试验方案如表1所示，其中应变均从0%加载到1.5%，具体试验介绍参见文献[18]。

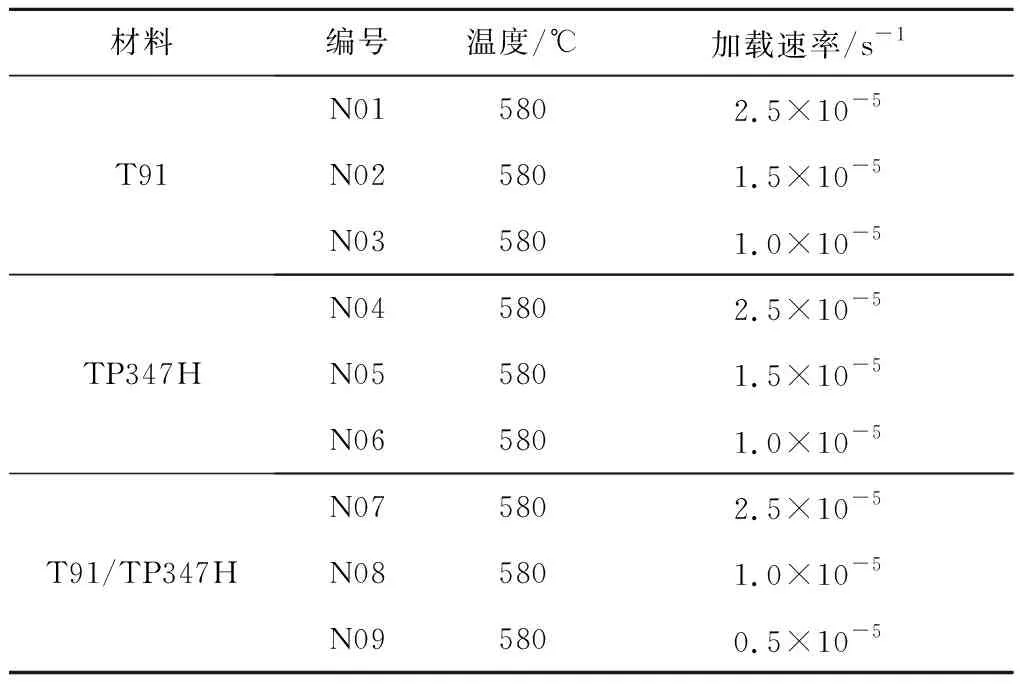
表1 试验方案Tab.1 Test plan

2 T91/TP347H异种钢焊接接头拉伸本构模型研究

当材料有显著强化率，而屈服流动不明显时，可以不考虑材料的塑性流动，用线性强化弹塑性力学模型，又称为双线性强化模型来描述其拉伸力学行为。

其应力解析式如下：

(1)

式中：σ为应力，MPa；ε为应变，%；σs为屈服极限，MPa；εs为屈服极限对应的屈服应变，%；E为弹性模量，MPa；E1为Tang模量，MPa。

对于屈服点不明显的材料，测量起来会有一定困难，一般规定应变为0.2%时的应力为屈服强度。因此，对双线性模型进行改进，将原双线性模型中的屈服点εs替换为0.2%，则σs可以通过计算得出。改进双线性模型的解析表达式如下：

(2)

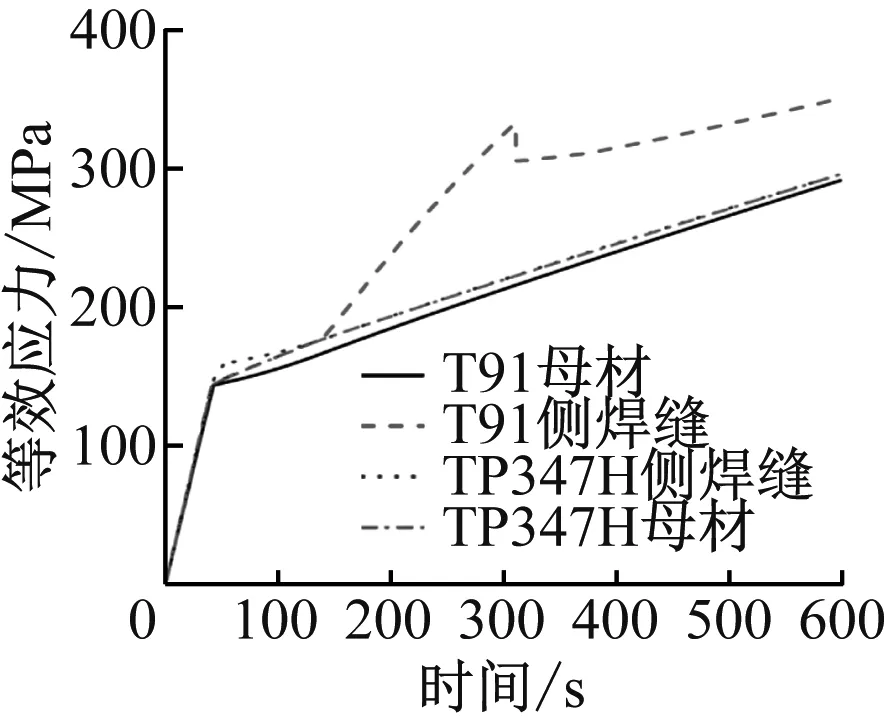
基于试验数据，采用最小二乘法拟合母材和焊接接头的双线性模型和改进双线性模型，试验结果和模型结果见图1～图3，拟合结果见表2。

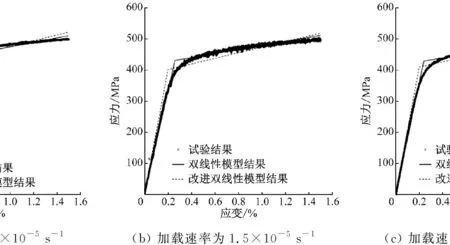
图1 不同加载速率下T91钢的试验及模型曲线Fig.1 Testing results and model curves of T91 steel at different loading rates

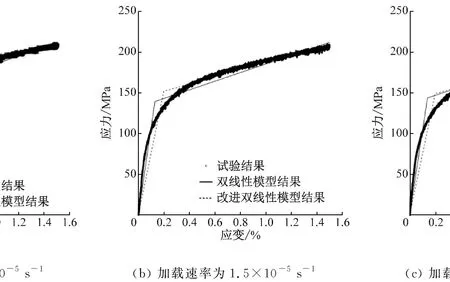
图2 不同加载速率下TP347H钢的试验及模型曲线Fig.2 Testing results and model curves of TP347H steel at different loading rates

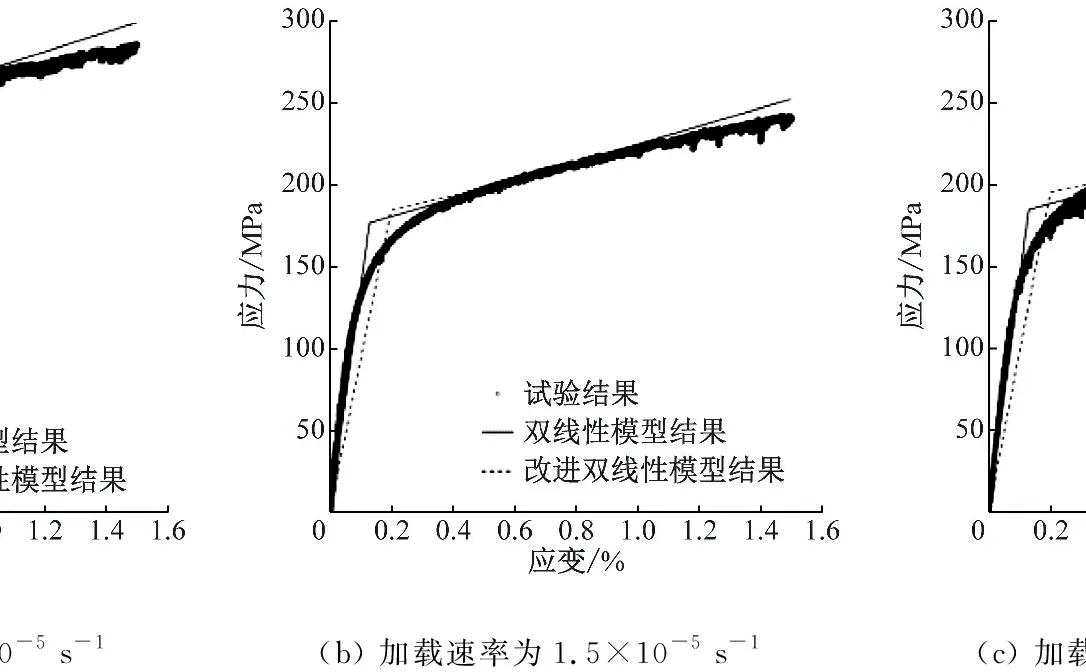
图3 不同加载速率下T91/TP347H异种钢焊接接头的试验及模型曲线Fig.3 Testing results and model curves of T91/TP347H dissimilar steel welded joints at different loading rates

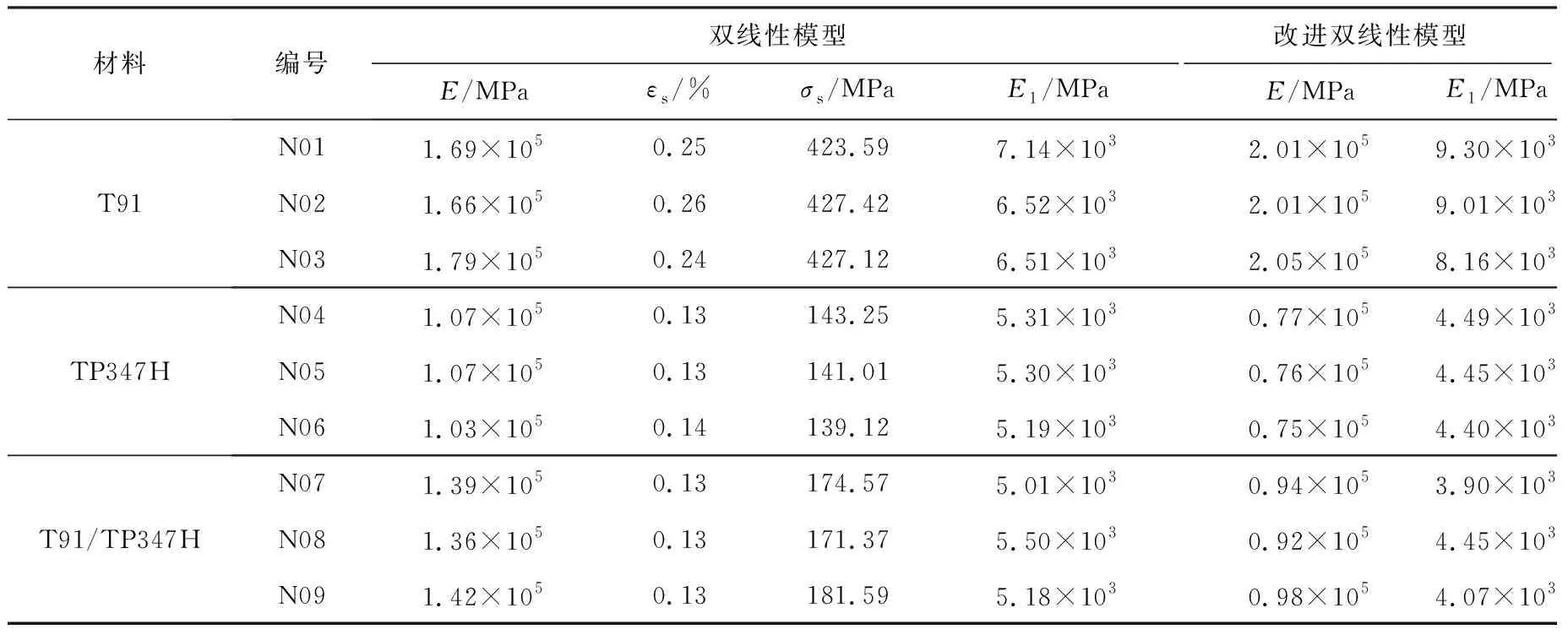
表2 双线性模型和改进双线性模型参数拟合结果Tab.2 The parameter fitting results of bilinear model and improved bilinear model

由图1～图3和表2可以得出：

(1) 10-5s-1量级的加载速率对T91钢、TP347H钢和T91/TP347H异种钢焊接接头拉伸的滞弹性力学行为影响较小。

(2) 双线性模型和改进双线性模型均能较精确地描述T91钢、TP347H钢和T91/TP347H异种钢焊接接头的高温拉伸行为。对于T91钢，在弹性阶段，双线性模型显得更为保守；而在塑性阶段，改进双线性模型显得更为保守。对于TP347H钢，在弹性阶段，2种模型均比较保守，但改进双线性模型过于保守；在塑性阶段，双线性模型比较保守，改进双线性模型与实际模型比较接近。

(3) T91/TP347H异种钢焊接接头的应力应变规律与TP347H钢类似。焊接接头屈服强度介于2种钢之间，但更靠近TP347H钢，即TP347H钢的性能对焊接接头整体性能的影响高于T91钢。

(4) 在实际工程应用中，建议用改进双线性模型来描述T91钢的高温拉伸行为；而TP347H钢和T91/TP347H异种钢焊接接头则采用双线性模型。

3 T91/TP347H异种钢焊接接头拉伸模拟研究

利用Ansys软件中plane13单元建立了试样的轴对称有限元模型，对称轴为y轴，如图4所示，模型共有846个节点(Node)，700个单元(Element)。为了模拟真实的试验约束，对模型一端进行全约束，另一端施加位移载荷。分别采用双线性模型和多线性模型模拟加载时间为600 s、加载速率为2.5×10-5s-1和加载时间为1 500 s、加载速率为1×10-5s-1时的试样拉伸过程，结果见表3。

图4 有限元模型网格划分图Fig.4 Meshing diagram of finite element model

由表3可知，对于双线性模型和多线性模型而言，等效应力的模拟结果随加载速率的变化较小，这与试验结果相吻合；但是双线性模型的等效应力模拟结果与T91/TPH347H异种钢焊接接头试验结果(见图3)差异较大，加载速率为2.5×10-5s-1和1×10-5s-1时对应的误差分别为28.28%和45.91%，而多线性模型的等效应力模拟结果与试验结果差异较小，2个加载速率下对应的误差分别为-10.51%和-5.13%。此外，拉伸模拟过程中，最大等效应力位置将发生变化，其具体位置的论述见3.1节。由表3还可知，双线性模型的最大等效应力模拟结果明显大于多线性模型，且M01、M02的最大等效应力位置不同，最大等效应力差异较大。由此可初步认为，多线性模型能更好地反映材料的拉伸本构关系。

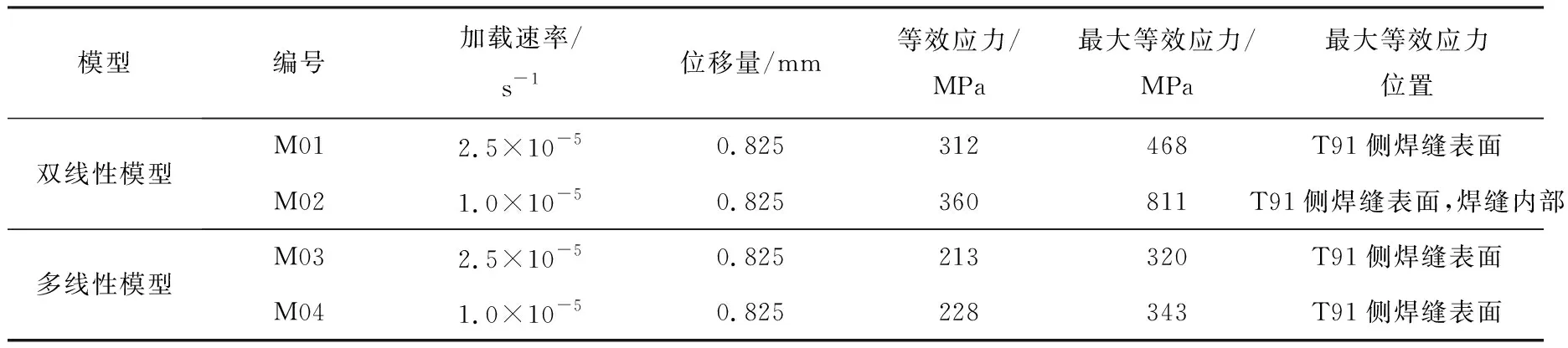
表3 模拟结果Tab.3 Simulation results

3.1 应力时间历程

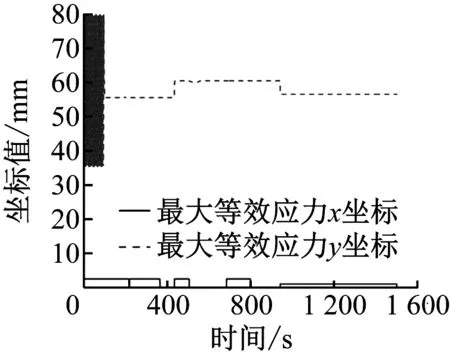
一般来说，异种钢焊接接头的失效多数发生在马氏体耐热钢一侧[1, 19-22]。由表3可知，最大等效应力主要集中在T91侧焊缝表面处，这与实际相符合，但最大等效应力初始并非出现在T91侧焊缝表面处，最大等效应力的x、y坐标随时间的变化如图5所示。

(a) M01

(b) M02

(c) M03

从图5可以看出，M01、M03和M04的最大等效应力点位置变化规律相同，最大等效应力值分别为468.107 MPa、320.495 MPa和343.309 MPa。在加载过程中，最大等效应力点从试样两端圆角处(x=35 mm和x=80 mm)经过试样中心(x=55 mm)转移到了试样表面x=2.5 mm处。在模型表面x=2.5 mm处取4个参考点：T91钢处(y=70 mm)为A点，T91侧焊缝处(y=60 mm)为B点，TP347H侧焊缝处(y=55 mm)为C点和TP347H钢处(y=45 mm)为D点。各点位置如图4所示，M01、M03和M04各点等效应力随时间的变化情况如图6(a)、图6(c)和图6(d)所示。

(a) M01

(b) M02

(c) M03

M02的最大等效应力位置前期与其他情况相同，但后期转移到焊缝内部(y=56.5 mm)并且最大等效应力达到了810.514 MPa。取相同的参考点A、B、C和D，再在x=1 mm处增加2个参考点：点E(y=60 mm)和点F(y=58.5 mm)。M02各点等效应力随时间的变化如图6(b)所示。

通过有限元模拟可以发现试验过程中难以观测到的现象，在加载初期，最大等效应力集中在试样的圆角附近，此时应力集中的效应占主导作用；在加载中期，最大等效应力在焊接接头的位置，并且在整个结构的正中间位置，此过程处于稳定状态；在加载后期，试样整体的应力比较大，由于各段材料的属性不同，特别是焊缝位置不同材料之间的相互作用更加明显。

图6(a)和图6(b)中，T91侧焊缝处(B点)应力突然快速上升的起点时间正好分别对应图5(a)和图5(b)中最大应力点位置由焊缝中心变到T91侧焊缝的时间。图6(b)中E点和B点曲线的交点所在时间，即对应图5(b)中最大等效应力变到焊缝内部的时间。参考点的最终等效应力及其与试验等效轴力的偏差如表4所示。

3.2 径向位移

拉伸应变为1.5%时，试样并不会发生明显的颈缩现象，因此在试验中会忽略试样直径的变化，即试样表面的径向位移，笔者通过有限元模拟把这种微小现象放大，结果如图7所示。

(a) M01

(b) M02

(c) M03

(d) M04图7 x方向变形图Fig.7 Deformation diagram in x-direction

图8给出了M01各参考点处的径向位移和外表面径向位移。从图8可以看出，T91钢处几乎没有径向位移，而T91侧焊缝处在加载前期也未发生明显的径向位移，在加载150 s后才开始有明显的径向位移，这与该点150 s后应力开始快速增大相对应。而TP347H钢和TP347H侧焊缝在加载后不久径向位移便开始匀速增加，其径向位移明显大于T91钢处的径向位移。但该模拟中的最大径向位移也只有0.035 87 mm，是试样测试部分长度的1.43%，最小径向位移为0.001 24 mm，是测试部分长度的0.05%，说明在TP347H钢侧略微发生了颈缩现象。

表4 参考点应力值及偏差Tab.4 Stress values and deviations of the reference points

(a) 参考点径向位移

(b) 外表面径向位移图8 M01各参考点的径向位移和外表面径向位移Fig.8 Radial displacement of reference points in M01

图9给出了M02各参考点的径向位移。从图9可以看出，T91钢处几乎没有径向位移，而T91侧焊缝处在加载前期也未发生明显的径向位移，在加载150 s后才开始明显的径向位移，这与该点150 s后应力开始快速增大相对应。而TP347H钢和TP347H侧焊缝在加载后不久径向位移便开始匀速增加，且径向位移明显大于T91钢处的径向位移。但试样上最大的径向位移也只有0.035 87 mm，是试样测试部分长度的1.43%，最小径向位移为0.001 24 mm，是测试部分长度的0.05%，说明在TP347H钢侧略微发生了颈缩现象。

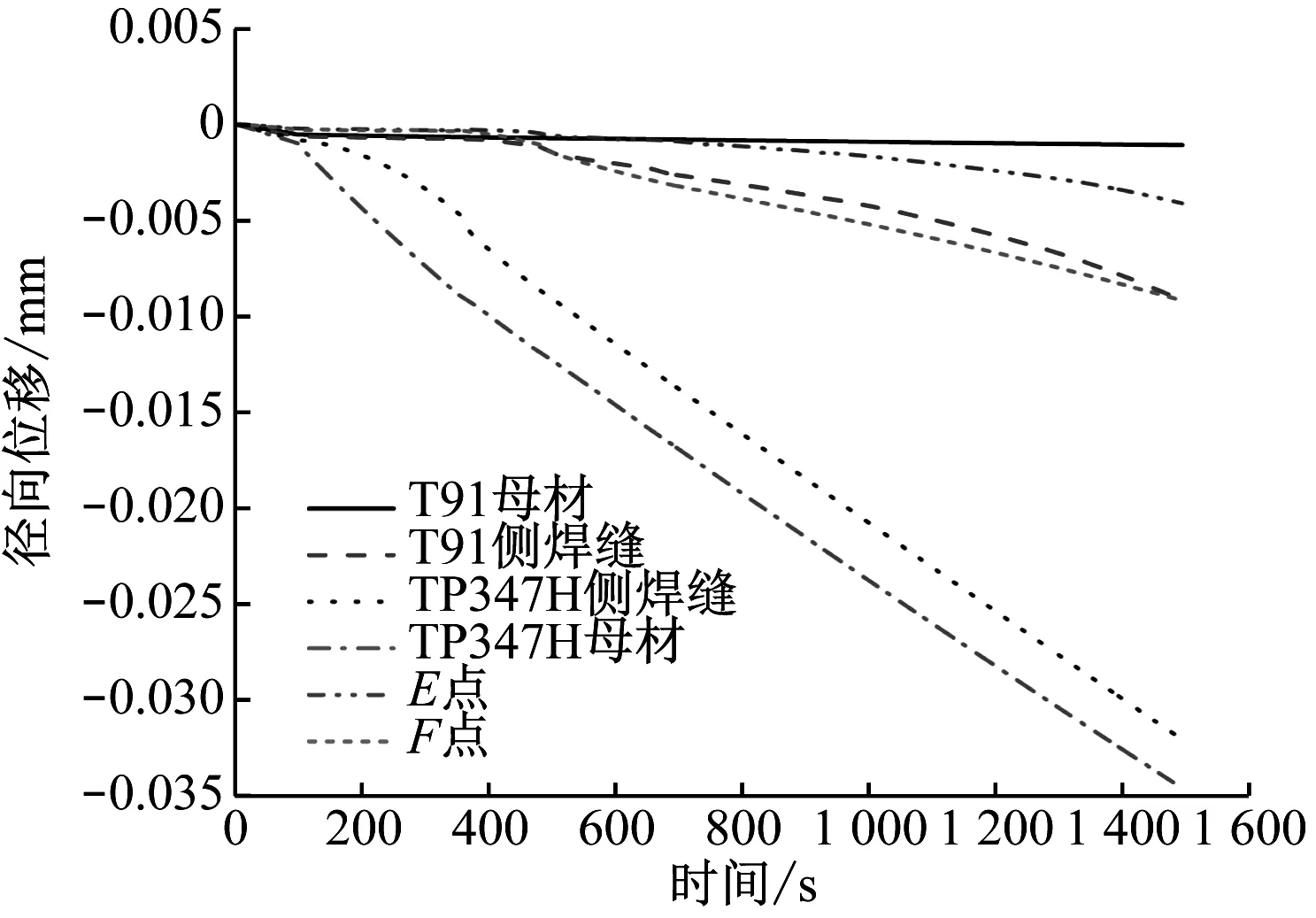
图9 M02各参考点的径向位移Fig.9 Radial displacement of reference points in M02

在加载前期的500 s内，T91钢及焊缝侧的各点都几乎没有径向位移，500 s后径向位移才开始了平缓增加。而TP347H钢及焊缝侧在加载开始100 s后径向位移就开始以一定速度增长，且径向位移明显大于T91侧。

图10给出了M02外表面径向位移和内部x=1 mm处各点的径向位移。从图10可以看出，外表面上焊缝处的径向位移变化与内部x=1 mm处相比较为连续，而内部x=1 mm焊缝处的径向位移在较近距离内连续突变几次。但不管是内部还是外部，TP347H侧的径向位移总是大于T91侧的径向位移。

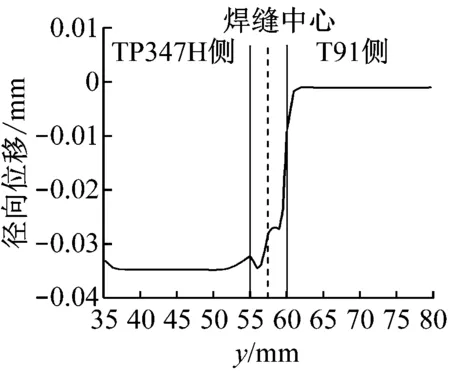
(a) 外表面径向位移

(b) 内部x=1 mm处径向位移图10 M02的外表面径向位移和x=1 mm处径向位移Fig.10 Radial displacement of M02 on the outer side and on the inner side of x=1 mm

图11给出了M03各参考点处的径向位移和外表面径向位移。可以看出，4个参考点的径向位移最初均近乎以线性规律增加。而在275 s左右后，A点、B点和C点的径向位移基本不变，TP347H侧D点径向位移开始非线性增加，最终达到0.033 73 mm。显然，径向位移都发生在TP347H侧，在y= 41.187 mm处达到最大，为0.125 06 mm，这一侧已经开始发生颈缩现象。

(a) 参考点径向位移

(b) 外表面径向位移图11 M03各参考点径向位移和外表面径向位移Fig.11 Radial displacement of reference points in M03

图12给出了M04各参考点处的径向位移和外表面径向位移。从图12可以看出，T91侧各点并没有发生明显的径向位移，变形量不足0.002 5 mm。而与T91侧相比，TP347H侧的各点都有一定的径向位移。由此可见，径向位移主要发生在TP347H侧，若增大应变量，TP347H侧最先开始发生颈缩现象。这是由于2种材料的本构模型不同，TP347H钢的高温拉伸性能要弱于T91钢。

(a) 参考点径向位移

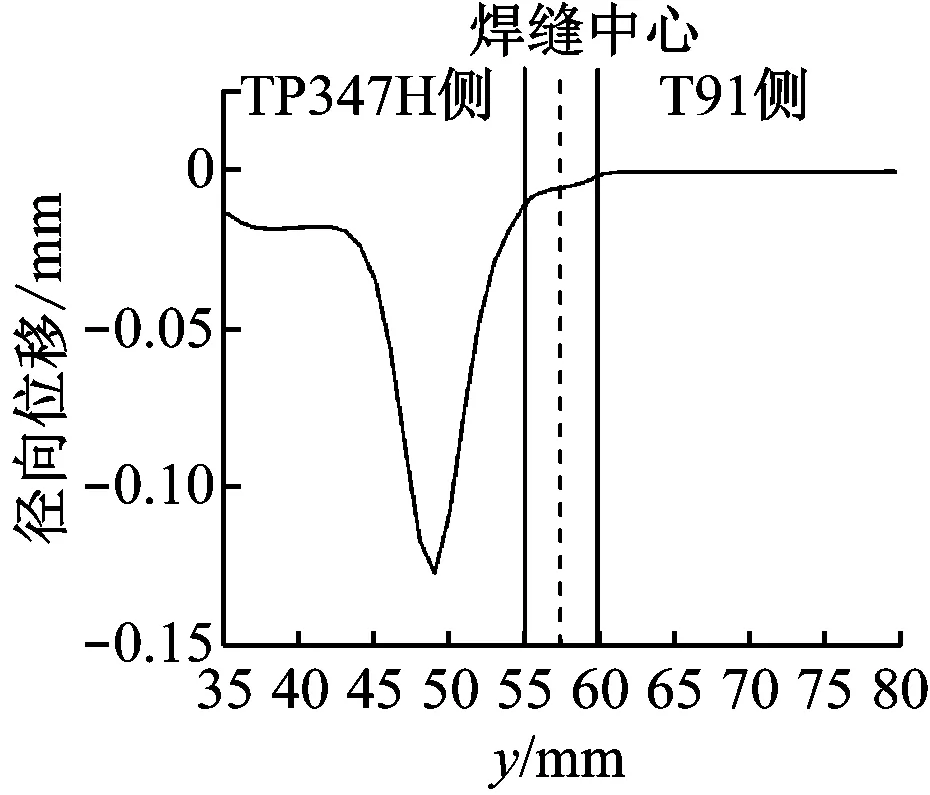
(b) 外表面径向位移图12 M04各参考点径向位移和外表面径向位移Fig.12 Radial displacement of reference points in M04

表5给出了各参考点径向位移及径向应变(εy)。从表5可以看出，TP347H侧的径向位移较大，横截面积减小，该侧是比较薄弱的一侧，若增大试验应变，则断裂位置可能出现在TP347H侧[9]。

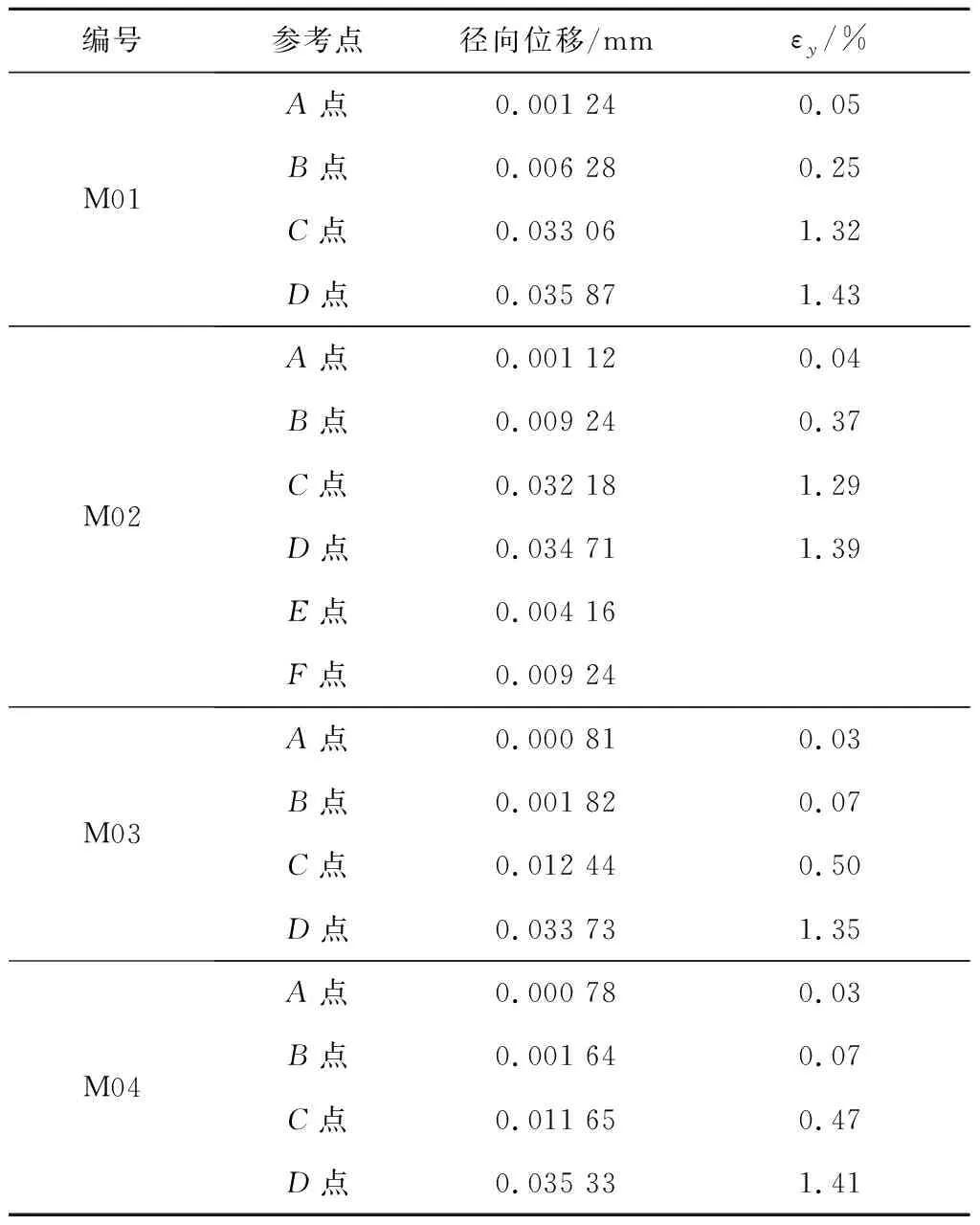
表5 各参考点径向位移及径向应变Tab.5 Radial displacement and strain of the reference points

3.3 表面应力及应力三轴度

最大等效应力位置基本都存在于试样的外表面，因此分析外表面各点的应力值和应力三轴度大小。应力三轴度可以反映应力场中三轴应力状态及其对材料变形的约束程度，因而会直接影响各点塑性变形的大小及断裂应变大小[22]。应力三轴度越大，应力状态更倾向于受拉应力状态，材料容易正断；应力三轴度越小，应力状态更倾向于受压应力状态，材料容易发生剪切断。

M01模拟的试样外表面各点的等效应力、第一主应力、第二主应力和第三主应力如图13(a)所示，外表面应力三轴度如图13(b)所示。可以看出，等效应力在T91钢和TP347H钢远离焊缝的位置基本保持在290 MPa左右，但从TP347H侧焊缝处向T91侧焊缝处过渡时，等效应力出现了起伏变化。

(a) 外表面各应力图

(b) 外表面应力三轴度图13 M01外表面各应力图和外表面应力三轴度Fig.13 Stress diagram and stress triaxiality on the external surface of M01

应力三轴度在外表面上的分布规律与等效应力的分布规律相似，但在T91侧焊缝与T91钢融合线位置多出一个峰。

M02模拟的试样外表面各点的等效应力、第一主应力、第二主应力和第三主应力如图14(a)所示，外表面应力三轴度如图14(b)所示。可以看出，由于试样内部变形不平稳，外表面的应力受到内部应力的影响，焊缝处等效应力出现了波动，导致其应力三轴度也出现剧烈波动，但最大等效应力仍出现在T91侧焊缝外。

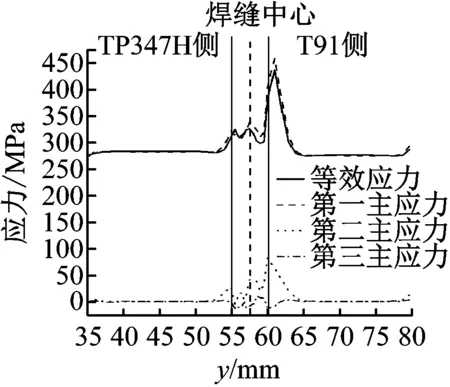
(a) 外表面各应力图

(b) 外表面应力三轴度图14 M02外表面各应力图和外表面应力三轴度Fig.14 Stress diagram and stress triaxiality on the external surface of M02

M02试样x=1 mm处各点的等效应力、第一主应力、第二主应力和第三主应力如图15(a)所示，外表面应力三轴度如图15(b)所示。从图15可以看出，由于材料之间的相互挤压，试样内部的应力较复杂，且主要集中在焊缝处。而焊缝内TP347H侧的等效应力高于T91侧，T91侧焊缝处的应力三轴度变成了负值。

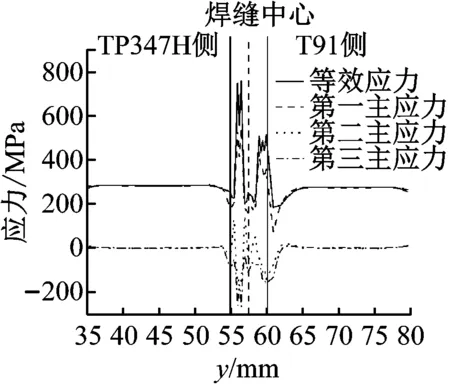
(a) x=1 mm处各应力图

(b) x=1 mm处应力三轴度图15 M02在x=1 mm处各应力图和应力三轴度Fig.15 Stress diagram and stress triaxiality in x=1 mm of M02

M03模拟的试样外表面各点的等效应力、第一主应力、第二主应力和第三主应力如图16(a)所示，外表面应力三轴度如图16(b)所示。由图16可知，多线性模型下的试样外表面等效应力分布规律与双线性模型基本相同，区别在于TP347H侧的变化和应力值的大小。TP347H侧各应力在外表面的分布是不平稳的，第一主应力和第二主应力都出现2个峰值和1个谷值，第三主应力出现1个谷值，3个主应力的谷值出现的位置与发生最大径向位移的点相对应。整体等效应力最大值在T91侧，最大等效应力为256.62 MPa。

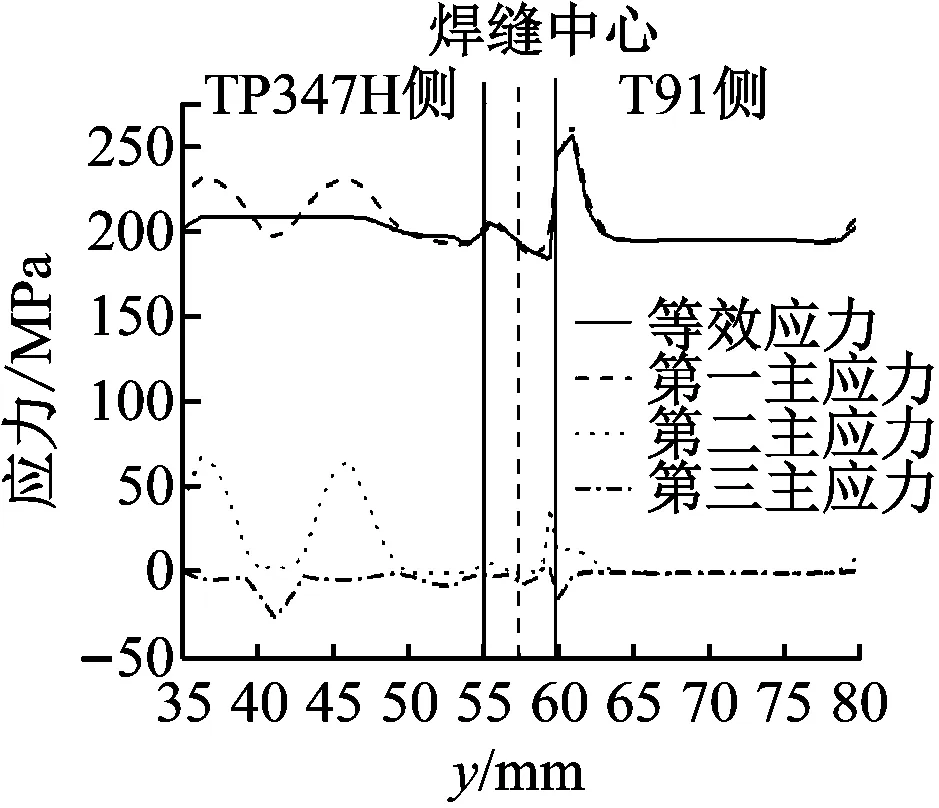
(a) 外表面各应力图

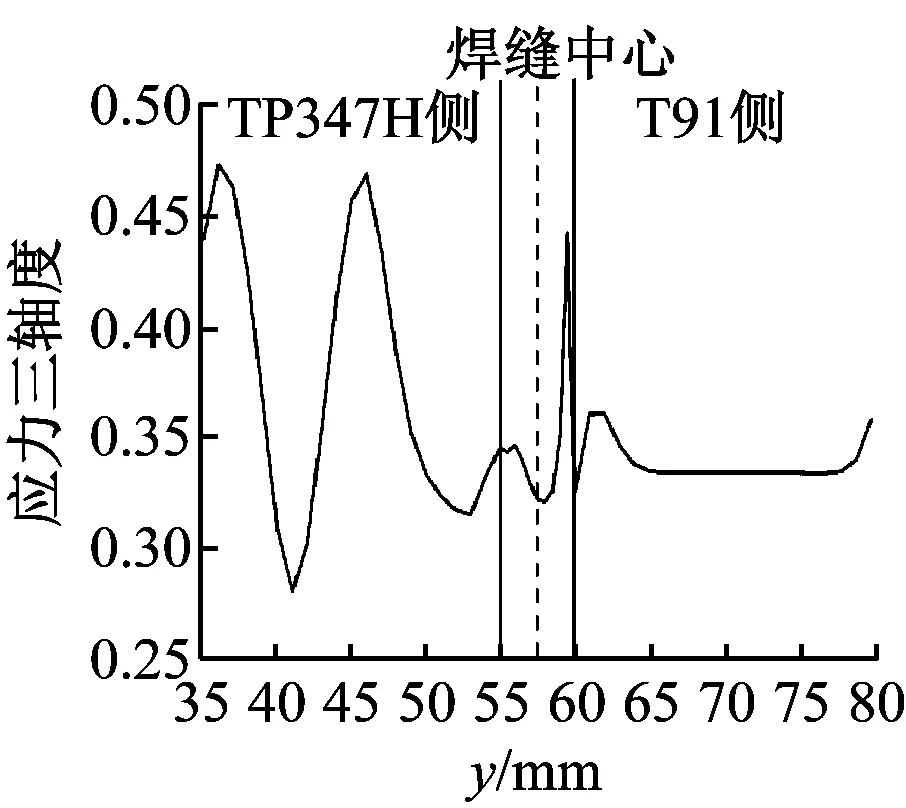
(b) 外表面应力三轴度图16 M03外表面各应力图和外表面应力三轴度Fig.16 Stress diagram and stress triaxiality on the external surface of M03

M04模拟的试样外表面各点的等效应力、第一主应力、第二主应力和第三主应力如图17(a)所示，外表面应力三轴度如图17(b)所示。可以看出，最大等效应力位置在T91侧焊缝位置，T91钢的等效应力、第一主应力、第二主应力和第三主应力的变化都很平稳。而在焊缝和TP347H侧虽然等效应力表现平稳，但其第一主应力、第二主应力和第三主应力都存在波动，因此焊缝和TP347H侧的应力三轴度也存在很大波动。

(a) 外表面各应力图

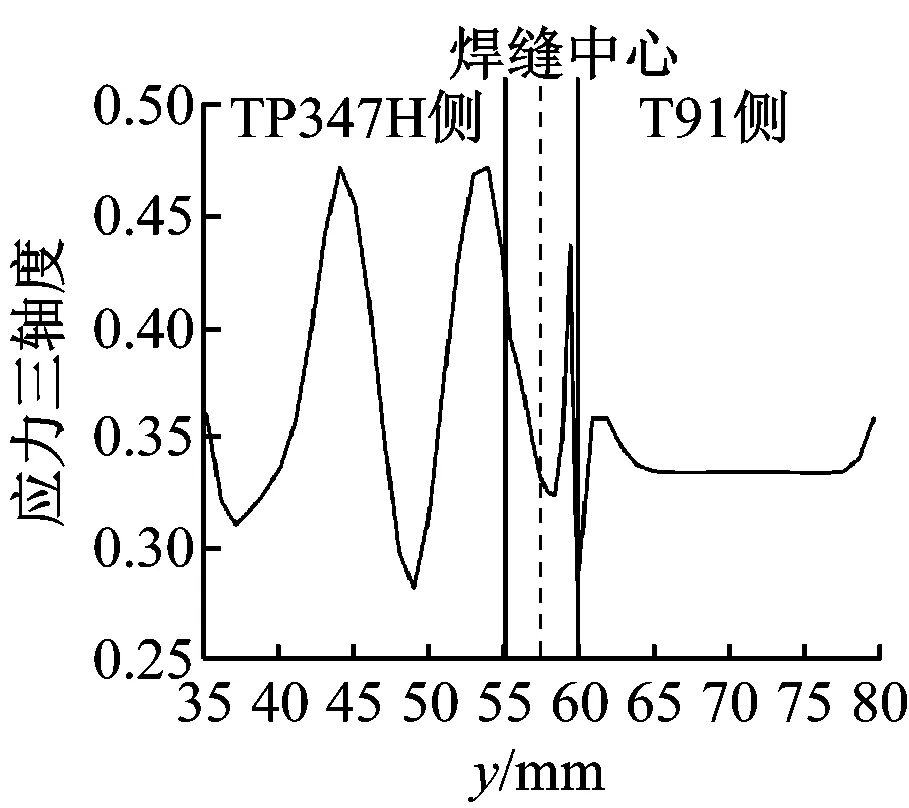
(b) 外表面应力三轴度图17 M04外表面各应力图和外表面应力三轴度Fig.17 Stress diagram and stress triaxiality on the external surface of M04

各模拟结果表明，T91/TP347H异种钢焊接接头易发生正断。双线性模型的模拟结果(M01和M02)表明，断裂位置很可能发生在T91侧的焊缝处，可能发生断裂位置附近的应力三轴度变化剧烈，当材料上某点处的应力三轴度变化较大时，该点就是该材料上的危险点；多线性模型的模拟结果(M03和M04)表明，T91侧焊缝和TP347H侧的应力三轴度较大，变化也较剧烈，是材料的危险点。

4 结 论

(1) 多线性模型的模拟结果偏差小于双线性模型的模拟结果偏差，且在T91侧焊缝处的偏差较小，符合实际情况，因此认为多线性模型能够更好地反映材料的拉伸本构关系。

(2) T91/TP347H异种钢焊接接头的薄弱位置在T91侧焊缝处附近，且位于材料外表面，但T91侧几乎没有发生径向变形，而TP347H侧出现径向变形，导致这一侧横截面积减少，应力三轴度变化较大，是比较薄弱的位置。