基于BP神经网络代理模型的翼型优化及领域自适应研究

陈晨铭， 郭雪岩， 常林森

(上海理工大学 能源与动力工程学院， 上海 200093)

风力机中的风轮叶片是获得较大风力发电功率的关键，翼型设计是风力发电机组叶片研发的核心任务。航空翼型通常不能完全用作风力机翼型，一般要求风力机翼型在设计工况下具有较高的升力系数和升阻比，在其他工况下有良好的失速性能[1]。

翼型优化方法主要有2种：一种是正问题设计法，先设计翼型后再进行模拟，然后根据结果调整翼型；另一种是反问题设计法，根据需要的结果，推算出翼型[2]。韩忠华[3]总结了Kriging模型及代理优化算法的相关研究进展，如通过增加样本点来提高代理模型精度的EI准则等。刘颖超等[4]通过Kriging代理模型优化汽轮机叶片顶端跨音速叶型。何磊等[5-6]通过深度学习的卷积神经网络，以压力图像作为样本输入、翼型曲线作为样本输出，实现了反问题设计。Tao等[7]通过主成分分析-深度信念(PCA-DBN)网络构造代理模型，采用拉丁超立方-适应度距离比-代理粒子群(LHS-FDR-SOPSO)算法对层流翼型和跨声速机翼进行优化。李润泽等[8]通过指定一个策略树，使用强化学习方法，从策略树中寻找最优策略，使得该策略下生成的翼型的气动性能符合要求。

领域自适应可以将从一个样本集学得的模型，迁移到另一个样本集，从而完成泛化[9]。笔者针对青藏高原气候特征的风场(最高风速为7 m/s左右)[10]，通过CST(Class function/Shape function Transformation)参数化方法实现翼型曲线与参数的转换，使用深度前馈网络构建代理模型，结合遗传算法对NACA64(3)-618风力机翼型进行优化，并将代理模型用于NACA64(3)-218和NACA64(3)-418翼型，实现领域自适应(或迁移学习)。

1 机器学习方法

某个神经网络如图1所示，每一层都包含神经元，第一层为输入层或可见层(v1～v3)，其中每一个神经元对应输入的特征向量的一个值，通过连接输送给下一层，中间层称为隐藏层(h1和h2)，其神经元接受与其连接的上一层神经元传递的值，重新构成向量，通过M-P神经元模型进行计算，如式(1)所示，得到的值传递给下一层，并通过最后一层(即输出层(o1))进行输出。理论上，输出可以是任意维度的向量，包含单个值。深度前馈网络由含有多个隐藏层的神经网络构成[9,11-12]。

图1 神经网络示意图Fig.1 Schematic diagram of neural network

y=f(ωTx+θ)

(1)

式中：y为该神经元的输出值；f(·)为某一函数，本文使用sigmoid函数；x为输入的向量；ω和θ为模

型的参数。

选定f(·)后，ω和θ就是需要调整的参数，调整参数的过程又称为训练神经网络。误差逆传播(error Back Propagation，BP)算法可以训练一个神经网络，但是由于标准BP算法只使用了梯度下降方法，而梯度下降方法可能收敛于局部最优而非接近全局最优，可能在梯度不明显的地方反复振荡，也可能在梯度突变的地方发散，所以BP算法也存在这一缺点[9,11-12]。LM(Levenberg-Marquardt)-BP算法是近似于牛顿法的正则化方法，牛顿法在一定条件下一直沿下降方向移动，有可能在其他情况下不收敛，而用了LM方法却能达到收敛[13-14]。贝叶斯正则化(Bayesian regularization)-BP算法通过LM方法更新权值和偏值，最小化平方误差和权重的线性组合，然后不断修正该线性组合进行迭代，以获得较好的神经网络泛化性[15]。LM方法的平方误差和权重的组合如式(2)～式(4)[16-17]所示。

(2)

(3)

M=αEW(w|A)+βED(D|w,A)

(4)

式中：D为含有N个样本的样本集，D={xm,tm}，其中xm和tm分别为第m个样本的输入特征向量和输出向量；w为神经网络参数；i表示维度；A为神经网络结构；ED(D|w,A)为由以w和A构成的神经网络计算得到的样本集D预测值的0.5倍平方误差和；y(xm,w,A)为以w和A构成的神经网络计算得到的预测值；EW(w|A)为以A为结构的神经网络中w的0.5倍L2范数平方；M为贝叶斯正则化函数；α和β为对应线性项的权重。

2 翼型优化设计

本文方法的优化设计流程图如图2所示，包括CST参数化方法、机器学习方法、代理模型和智能优化方法。首先通过CST参数化方法、B样条曲线和拉丁超立方采样生成1 000个翼型曲线样本，然后使用计算流体力学(CFD)方法进行模拟计算，获得升力系数Cl和阻力系数Cd，使用其中150个翼型样本来训练深度前馈网络代理模型，通过代理模型和遗传算法在给定区间内对升阻比Cl/Cd进行寻优，并通过CFD再次验证获得的最优解的精度。

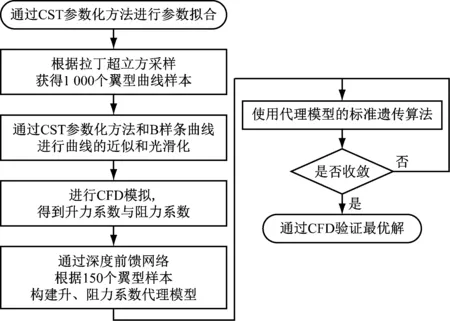
图2 优化设计流程图Fig.2 Flow chart of optimal design

笔者选用NACA64(3)-618翼型，采用4阶CST参数化方法进行参数拟合。在一定区间，根据拉丁超立方采样，获得1 000个样本。之后通过CST参数化方法还原出301个坐标点数据，再将这些坐标点作为控制点，用B样条曲线进行曲线的近似和光滑化，得到2 001个坐标点数据。样本翼型区域与拟合翼型如图3所示，其中X、Y分别为相对横坐标和相对纵坐标。

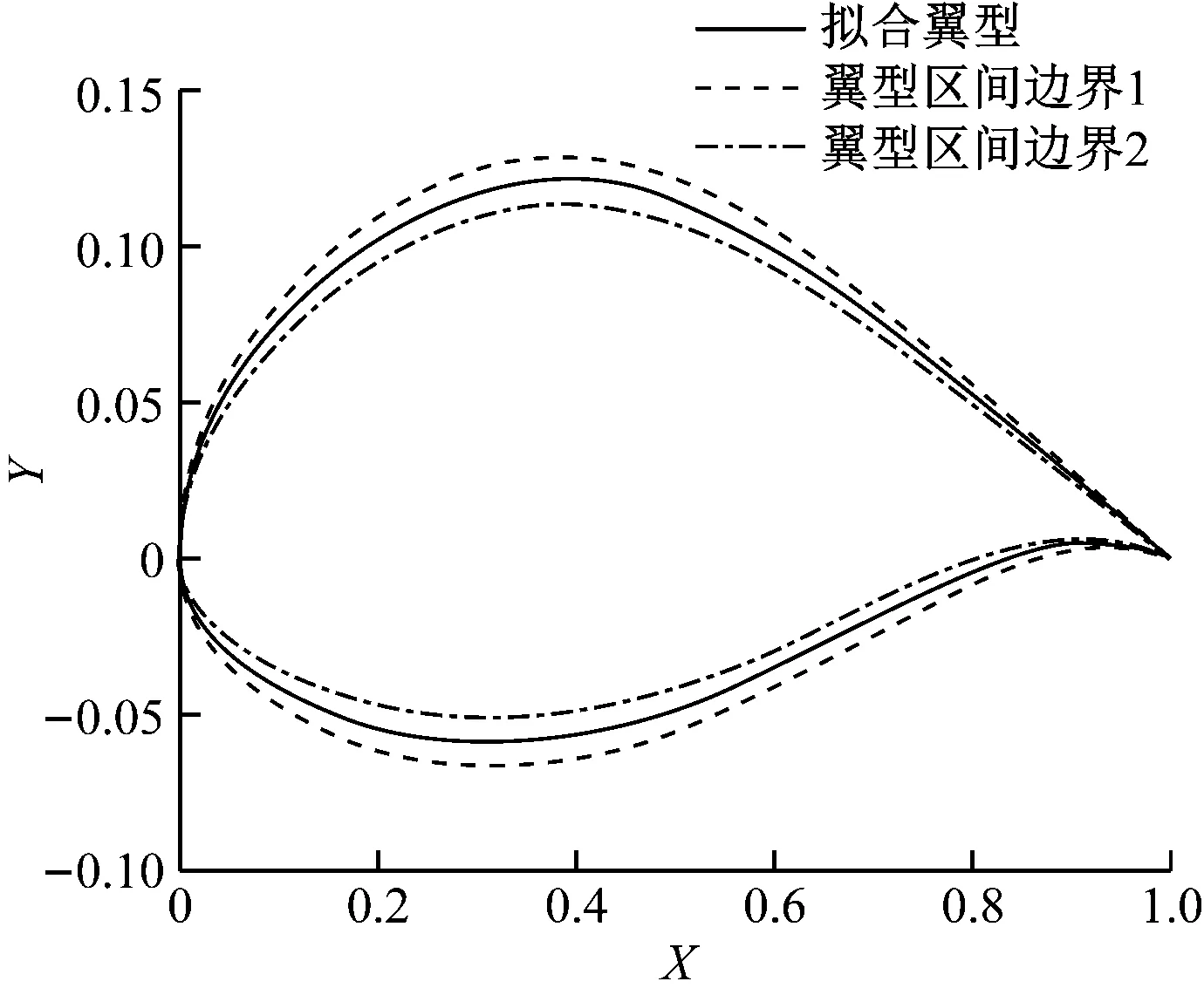
图3 样本翼型区域与拟合翼型Fig.3 Sample airfoil region and fitting airfoil

本文使用的是C型网格，使用Pointwise软件生成网格。由于参数化时生成的翼型是B样条曲线，且有2 001个坐标点，不使用软件自带的基于Bézier原理生成的三次样条插值方法[18]，其效果更好，通过设置参数，最后获得翼型网格。某一个样本翼型的网格如图4所示。

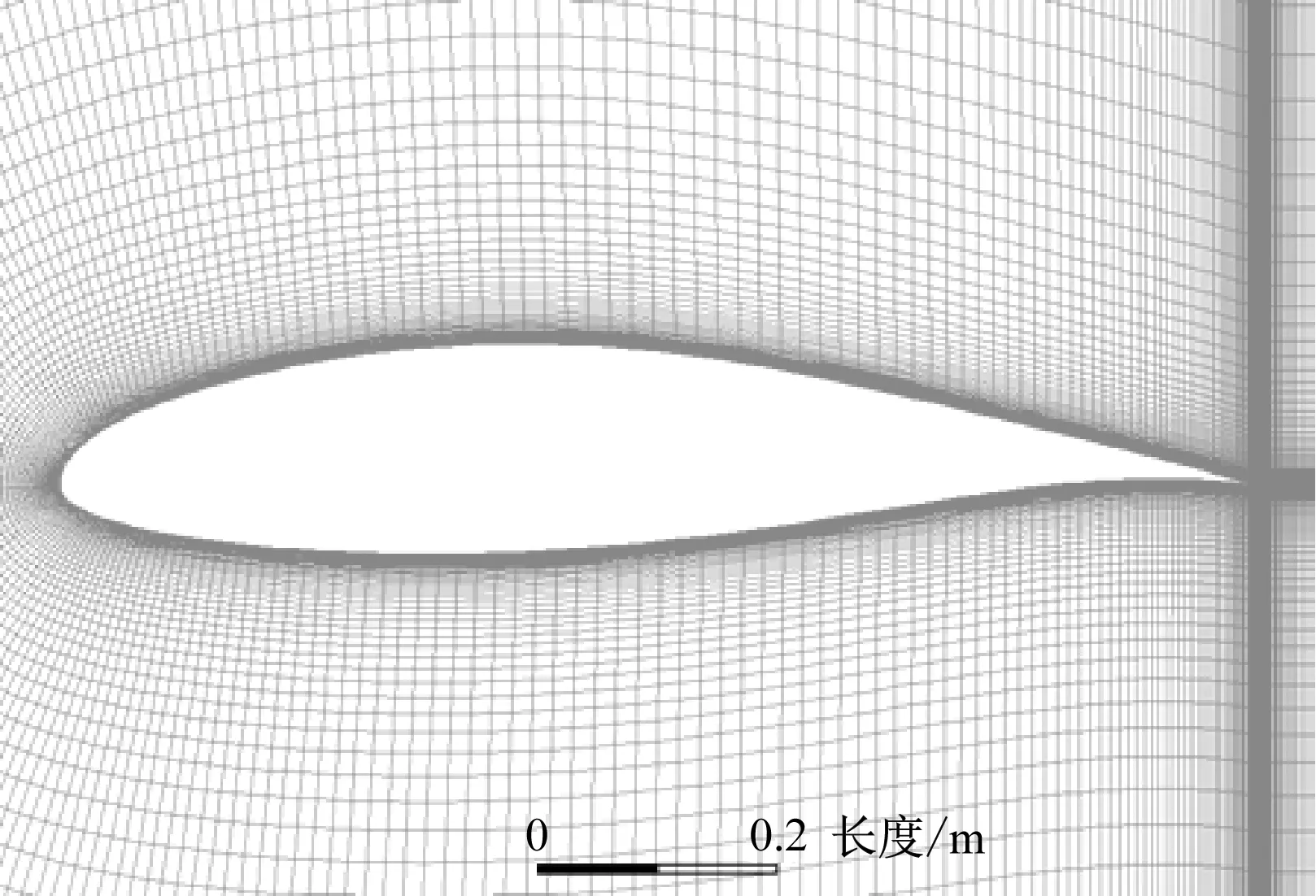
图4 某一个样本翼型的网格Fig.4 Mesh of a sample airfoil

使用SSTk-ω湍流模型，以空气作为流体，入口绝对速度为7.303 7 m/s，攻角为6°。使用SIMPLEC格式，动量方程使用三阶MUSCL离散格式，湍动能和比耗散率均使用二阶迎风离散格式，其余采用默认设置。迭代次数为2 000。

本文使用2种神经网络，每种神经网络再分为2个，分别输出升力系数和阻力系数，总共生成2种、4个神经网络代理模型。神经网络1使用1层隐藏层，为10个节点，通过LM-BP算法进行训练。神经网络2使用2层隐藏层，各5个节点，通过贝叶斯正则化-BP算法进行训练。150个样本分为训练集、验证集和泛化集，每个集对应的样本数分别为150个样本数的70%、15%和15%。通过4阶CST参数化方法将光滑化后的翼型曲线再次拟合成参数，作为神经网络的输入特征向量，采用之前CFD计算的升力系数和阻力系数分别作为输出。最终得到神经网络1升力系数代理模型、神经网络1阻力系数代理模型以及对应的神经网络2升力系数代理模型和神经网络2阻力系数代理模型。4个神经网络代理模型预测的最大相对误差如表1所示。

表1 预测结果的最大相对误差Tab.1 Maximum relative error of prediction results %

使用标准遗传算法，优化的目标函数如下：

(5)

(6)

式中：b为CST参数；bmin和bmax为b的最小值和最大值；fl和fd分别为之前训练的升力系数和阻力系数代理模型中的神经网络函数，使用CST参数b作为输入，升力系数Cl和阻力系数Cd分别作为输出；f(b)为需要最优化的升阻比，符号为负；A1为翼型面积；A0为原翼型面积。

遗传算法设置精度为10-10，种群最大迭代次数为50，共1 000个个体。式(5)中代理模型使用神经网络1和神经网络2分别进行计算。式(6)中代理模型使用神经网络2进行计算。总共得到3个优化翼型。

3 优化翼型的气动特性

通过神经网络1和式(5)得出的优化翼型1与拟合翼型的对比曲线如图5所示。通过神经网络2和式(5)得出的优化翼型2与拟合翼型的对比曲线如图6所示。通过神经网络2和式(6)得出的优化翼型3与拟合翼型的对比曲线如图7所示。采用CFD方法后，优化翼型3与拟合翼型压力系数(Cp)对比如图8所示，优化翼型3与拟合翼型上、下翼面摩阻系数(Cf)对比如图9和图10所示，优化翼型3的流线与压力如图11所示。上翼面平均压力系数降低，下翼面平均压力系数提高，导致升力系数提高。由于是低速翼型，仅在上翼面末端出现流动分离，上翼面末端和前驻点的摩阻系数有较大波动，阻力系数降低的原因较为复杂。

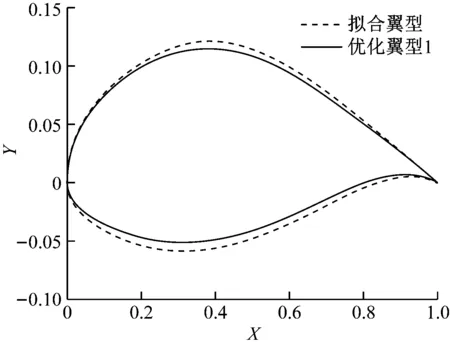
图5 优化翼型1与拟合翼型比较Fig.5 Comparison between optimized airfoil 1 and fitting airfoil

图6 优化翼型2与拟合翼型比较Fig.6 Comparison between optimized airfoil 2 and fitting airfoil

图7 优化翼型3与拟合翼型比较Fig.7 Comparison between optimized airfoil 3 and fitting airfoil

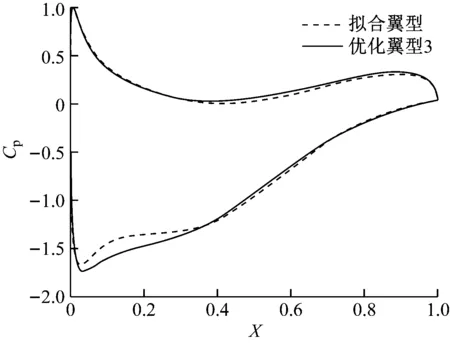
图8 优化翼型3与拟合翼型压力系数比较Fig.8 Comparison of pressure coefficient between optimized airfoil 3 and fitting airfoil

图9 优化翼型3与拟合翼型上翼面摩阻系数比较Fig.9 Comparison of skin friction coefficient on the upper surface between optimized airfoil 3 and fitting airfoil

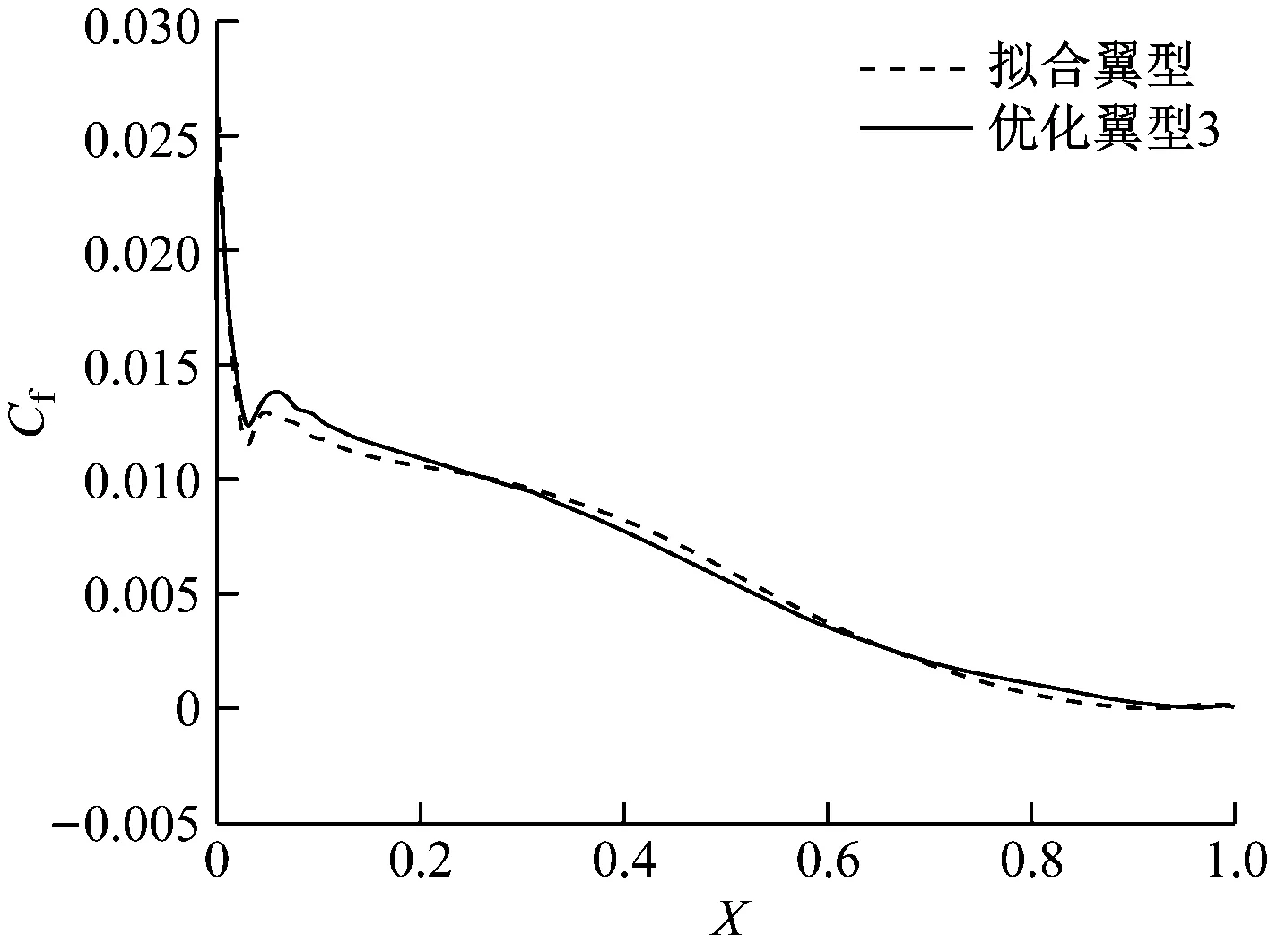
图10 优化翼型3与拟合翼型下翼面摩阻系数比较Fig.10 Comparison of skin friction coefficient on the lower surface between optimized airfoil 3 and fitting airfoil

图11 优化翼型3的流线和压力Fig.11 Streamline and pressure of optimized airfoil 3

由CFD模拟计算可得，拟合翼型的升力系数为1.022 01，阻力系数为0.021 37，升阻比为47.817 9。优化翼型1的升力系数为1.062 97，阻力系数为0.020 59，升阻比为51.638 0。与拟合翼型相比，优化翼型1的升力系数提高了4.01%，阻力系数降低了3.69%，升阻比提高了7.99%。优化翼型2的升力系数为1.065 04，阻力系数为0.020 60，升阻比为51.704 2。与拟合翼型相比，优化翼型2的升力系数提高了4.21%，阻力系数降低了3.62%，升阻比提高了8.13%。优化翼型3的升力系数为1.063 41，阻力系数为0.021 28，升阻比为49.980 4。与拟合翼型相比，优化翼型3的升力系数提高了4.05%，阻力系数降低了0.42%，升阻比提高了4.52%。

由代理模型计算得到：优化翼型1的升力系数为1.062 07，阻力系数为0.020 60，升阻比为51.561 4，升阻比相对误差为0.148%；优化翼型2的升力系数为1.065 16，阻力系数为0.020 61，升阻比为51.685 1，升阻比相对误差为0.037%；优化翼型3的升力系数为1.063 26，阻力系数为0.021 29，升阻比为49.951 9，升阻比相对误差为0.057%。

4 代理模型领域自适应检验

4.1 直接预测相似翼型

直接用NACA64(3)-618翼型的神经网络2的2个代理模型对NACA64(3)-218和NACA64(3)-418翼型的升力系数和阻力系数进行预测分析，在相同工况和CFD求解设置下对2种翼型进行模拟，并对结果进行分析。这种方法属于领域自适应，通过一个样本集生成的模型去预测另一个样本集[9]。

通过LM-BP算法生成的代理模型预测得到NACA64(3)-218、NACA64(3)-418和NACA64(3)-618翼型在本文工况下的升力系数分别为0.901 9、0.921 4和1.016 3，相对误差分别为18.45%、3.68%和5.852 3×10-5；阻力系数分别为0.018 2、0.019 5和0.021 3，相对误差分别为0.75%、0.28%和0.02%。通过贝叶斯正则化-BP算法生成的代理模型预测得到的3种翼型的升力系数分别为0.898 0、0.915 6和1.016 4，相对误差分别为17.94%、3.02%和1.710 0×10-5；阻力系数分别为0.018 2、0.019 5和0.021 3，相对误差分别为0.40%、0.23%和0.03%。通过CFD模拟得到的3种翼型的升力系数分别为0.761 4、0.888 7和1.016 4，阻力系数分别为0.018 1、0.019 5和0.021 3。2种阻力系数代理模型的相对误差如表2所示。

表2 阻力系数相对误差Tab.2 Relative error of drag coefficient %

因为工况相同、模拟方式相同，NACA64(3)-218、NACA64(3)-418和NACA64(3)-618翼型较为相似，所以阻力系数代理模型具有较好的精度。

4.2 修正系数调整

根据前文优化流程，对NACA64(3)-218和NACA64(3)-418翼型各生成50个翼型的样本集。对之前获得的代理模型通过修正系数法进行调整，如式(7)和式(8)所示。

(7)

(8)

通过对NACA64(3)-218和NACA64(3)-418 2种翼型拟合后的翼型计算修正系数，分别对包含50个样本的样本集进行预测和CFD模拟检验，结果如表3所示。

表3 领域自适应方法的最大相对误差Tab.3 Maximum relative error by domain adaption method %

通过修正系数法，阻力系数代理模型的精度更高，升力系数代理模型精度也有一定提升。但升阻比的精度不佳，主要原因是升力系数代理模型不精确，部分数据甚至不如直接用拟合后的翼型相关数据替换。

4.3 结果分析

由于翼型的阻力系数主要是由湍流边界层的摩擦导致的。不可压缩流动平板边界层中表面的总摩阻系数与平板特征尺度有关，不可压缩流动沿曲面边界层速度分布与Pohlhausen型参数λ有关，其中λ为边界层坐标点横坐标x的函数，与物面的形状密切关联[19]，这些可以作为本阻力系数代理模型精度较高的一个参考依据。

而翼型的升力系数是由上下表面的压力差产生的，压力差与翼型曲线关系较为复杂，故升力系数代理模型的精度较低。

5 结 论

(1) NACA64(3)-618翼型的优化结果表明，优化后翼型的升力系数可以达到1.063 41，阻力系数为0.021 28，升阻比为49.980 4，升力系数提高了4.05%，阻力系数降低了0.42%，升阻比提高了4.52%。

(2) 本文优化方法将高维数据降低为低维数据，且保留了比较完整的翼型数据。

(3) 代理模型可以大幅提高预测的效率，并保持一定的精度。同时，代理模型也可以用于类似的NACA翼型的升力系数和阻力系数预测，其中阻力系数代理模型对其他翼型有较好的泛化性。代理模型能够在较短时间内和较严苛条件下得到较好的翼型。