塔式锅炉炉内烟气流动的非线性特性分析及热偏差控制

赵晏锋， 杨 茉,2， 王文帅

(1. 上海理工大学 能源与动力工程学院， 上海 200093； 2. 上海建桥学院， 上海 201306)

四角切圆燃烧因其具有较好的燃烧稳定性和风煤混合均匀性成为超超临界锅炉最主要的燃烧方式之一。然而，切圆燃烧方式中存在的热偏差问题使得炉内各管组的平均温度下降，锅炉的发电效率也随之降低。

国内外许多学者对切圆锅炉的热偏差问题进行了深入的研究。Park等[1]发现炉膛中上部的残余旋转导致烟气进入水平通道后在左右方向上的速度分布不均，从而引起热偏差。Akkinepally等[2-4]同样认为炉内上部的残余旋转是造成热偏差的主要原因之一。

目前，对切圆锅炉热偏差机理的研究大多针对Π型锅炉，对于塔式切圆锅炉热偏差问题的研究还相对较少。Wu等[5]对一台1 000 MW塔式锅炉的热偏差形成机理进行了较为详细的数值研究，结果表明由于切圆燃烧产生的旋流具有较大的动量强度，燃尽风区域产生的切圆直径较大，导致炉膛上部中心区域附近的煤炭颗粒无法燃尽，因此中间区域与两侧区域的过热器吸热量存在明显差异。也有部分学者从非线性的角度来分析塔式切圆锅炉烟气侧热偏差的形成机理。王慧等[6]针对一台具有对称结构的塔式锅炉炉内的流动问题建立了一个简化的二维模型并进行了冷态模拟，结果表明无论采用层流还是湍流模型，随着喷口雷诺数Re的增大，炉内流场均由对称向非对称转变。赵明等[7]建立了一个几何结构完全对称的三维塔式锅炉模型，模拟了炉内的流场和温度场，发现即使锅炉的几何结构完全对称，其温度场也有可能是不对称的，同时通过微调对称方位上某一侧燃烧器的喷口速度使边界条件不完全对称，可以得到较为对称的流场和温度场。Yang等[8]对文献[7]中的锅炉炉内流动的非线性特性进行了数值研究，并通过改变喷嘴的水平角度使炉内的温度场更加对称。陈凯等[9]建立了一个简化的二维对冲炉膛模型，研究了不同Re下冷态流场的对称性，并利用频谱分析法研究了对冲射流特征解的非线性特性。

近年来，许多学者开始从各个角度对流动与传热过程的非线性特性进行研究，如二维方腔[10]与封闭圆内开缝圆[11]的自然对流问题以及突扩[12]与突缩[13]管道内的强制流动与换热问题等。 初值依赖是大多数非线性问题具有的特性之一。吴群刚等[14]对二维方腔斜进风对流换热问题进行了数值模拟与烟可视化实验，发现使用不同的初始流场计算迭代至收敛后，大漩涡的位置会偏向另一侧。杨茉等[15]研究了圆内开缝圆环自然对流换热数值解的唯一性问题，发现以不同的环状流为初始流场进行计算时最终结果收敛于不同的环状流型，这是由物理问题本身的不唯一性引起的。

然而，鲜有学者针对锅炉炉内非线性流动的初值依赖特性进行研究，因此笔者延续王慧等[6-8]的基本观点，进一步探讨锅炉炉内流动的非线性特性。以某台具有对称结构的1 000 MW塔式锅炉为研究对象，建立了一个简化的三维模型，并首次提出了顺序启动以及对角启动的控制策略，依据非线性问题的初值依赖特性，通过数值模拟探讨了同时启动、对角启动和顺序启动3种不同的启动方式对炉内流场、温度场以及炉膛出口烟气侧热偏差的影响。

1 物理模型

以某台1 000 MW塔式锅炉为研究对象，从中抽象出一个简化的三维模型，如图1所示，其中P1截面为Y=0 m截面，L1～L5分别是P2～P6截面沿炉膛宽度方向上的中心线。锅炉高度为110 m，宽度和深度均为21.48 m。如图2所示，该锅炉采用同心切圆燃烧。锅炉本体沿竖直中心线完全对称，笔者研究的主要是上游区域的流动及炉膛出口处的热偏差情况，因此省略了换热面区域的各受热面。同时，由于下游区域的流动对上游区域流动的影响很小，炉膛顶部拐角处的牵引效应造成的烟气偏斜对上游区域流动的影响可忽略不计。

图1 塔式锅炉简化模型Fig.1 Simplified model of the tower boiler

图2 同心切圆燃烧示意图Fig.2 Schematic diagram of concentrically and tangentially fired system

2 数值方法

2.1 控制方程

锅炉炉内的燃烧是包含复杂化学反应的气固两相混合流动过程，但其仍然遵循基本的质量守恒、动量守恒、能量守恒及化学组分平衡原理。

连续性方程为：

(1)

动量守恒方程为：

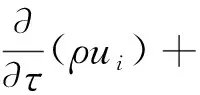
(2)

能量守恒方程为：

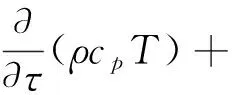
(3)

化学组分平衡方程为：

(4)

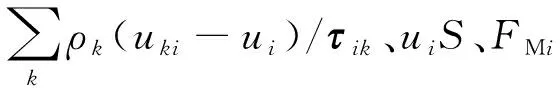
(5)

式中：μ为动力黏度；δij为克罗内克变量。

2.2 边界条件

2.2.1 出入口边界条件

各喷嘴全部采用速度入口边界条件，出口采用流动出口边界条件，表1给出了锅炉最大连续蒸发量(BMCR)工况下各一、二次风的速度及温度。煤粉质量流量及粒径均采用设计值，其直径遵循Rosin-Rammler分布。

表1 速度入口边界条件Tab.1 Velocity-inlet boundary conditions

2.2.2 壁面边界条件

采用无滑移、无质量交换的壁面条件，对近壁面采用标准壁面函数，依据设计值，将冷灰斗区域壁面温度设为680 K，主燃区壁面温度设为740 K，换热面区域壁面温度设为700 K。

2.2.3 煤种

该锅炉选用神府东胜煤作为设计煤种，其成分如表2所示，低位发热量为23.42 MJ/kg。

表2 煤质分析Tab.2 Coal quality analysis %

2.3 网格划分及独立性验证

运用ICEM软件分区域进行网格划分，冷灰斗区域采用较大的四面体网格，主燃区及换热面区域采用六面体网格，由于燃烧器喷嘴附近及近壁面区域的计算精度要求较高，对这些区域的网格进行了加密处理(见图3)，考虑到喷嘴射流方向与网格方向间的相互关系，在水平截面沿对角方向进行了十字划分，同时对每一小块区域采用Y型网格划分(见图4)，以提高网格质量。

图3 网格局部加密Fig.3 Partial densification of grid

图4 截面Y型网格划分Fig.4 Y-block grid division of cross section

为进行网格独立性验证，模拟了BMCR工况下炉膛的出口平均温度，网格数量依次加密为之前的1.3倍。如图5所示，当网格数量达到296万后，炉膛出口平均温度的变化相对较小，在不影响计算精度的前提下，考虑到计算机资源的限制，选用296万网格数量进行计算。

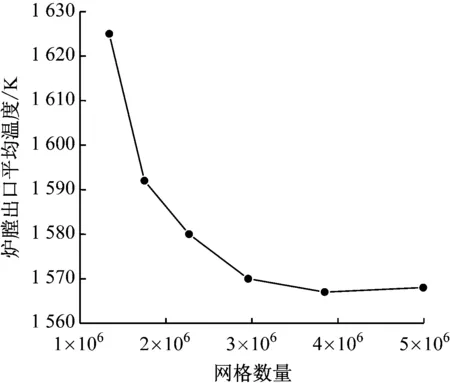
图5 网格独立性验证Fig.5 Grid independence verification

2.4 数值方法及准确性验证

气相湍流模型采用带有旋流修正的Realizablek-ε模型，离散相模型采用随机轨道模型，挥发分的析出采用双竞争反应热解模型，挥发分气相湍流燃烧采用混合分数-概率密度函数(PDF)模型，焦炭的燃烧采用动力-扩散控制模型，炉内的辐射换热采用P1模型，采用SIMPLE算法处理压力与速度的耦合，动量守恒方程和能量守恒方程均采用QUICK格式进行差分。

如表3所示，为了验证数值方法的准确性，笔者模拟了BMCR工况下炉膛出口平均温度和NOx质量浓度，并与对应的实测值、设计值进行了比较，发现炉膛出口平均温度模拟值稍高于设计值，这可能是由于省略了各受热面使得部分热量未被吸收，但其误差仍在合理范围内，在一定程度上可以证实该数值方法的可靠性。

表3 模拟值与设计值的对比Tab.3 Comparison between the simulated and design values

3 结果与分析

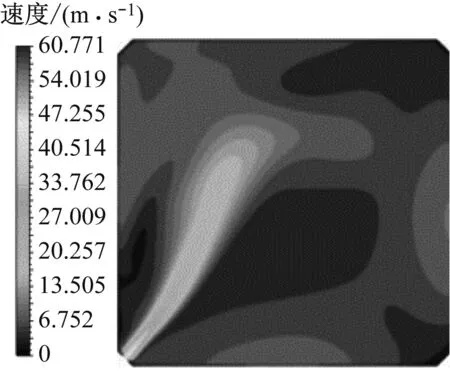
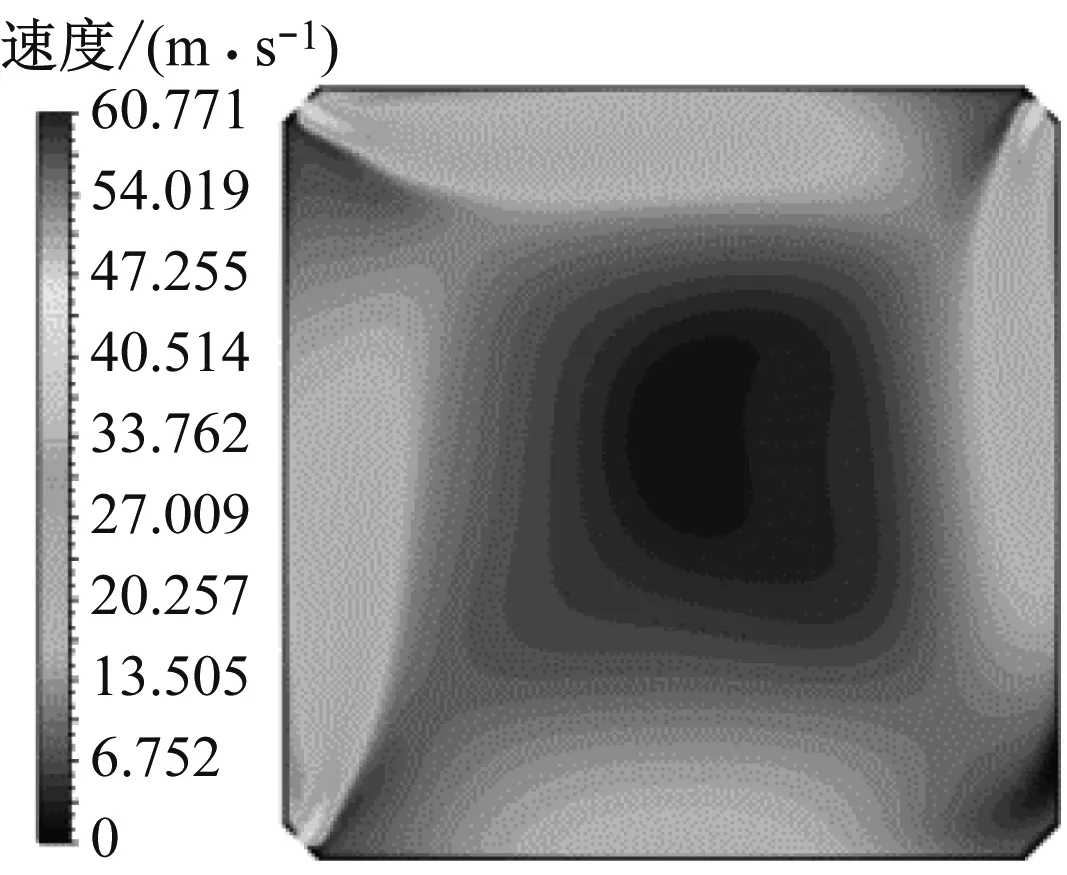
为了便于对结果进行分析，表4列举出了图1中6个研究截面的名称及具体位置。本文笔者关注的是炉内非线性流动的初值依赖特性，具体来说就是通过不同的启动方式建立不同的初始流场，期望获得较为良好的终态流场与温度场。图6和图7分别给出了冷态工况下顺序启动和对角启动时某一次风喷嘴截面的速度场。顺序启动，即首先开启一个角的喷嘴，然后按照一定的顺序依次启动其他3个角的喷嘴；对角启动指的是首先开启一个对角上的2组喷嘴，再开启另一个对角上的2组喷嘴。

表4 各截面位置及名称Tab.4 Location and name of each section

(a)

(b) CB角开启

(c) CBA角开启

(d) CBAD角全开图6 顺序启动的速度场Fig.6 Velocity field of sequential startup mode

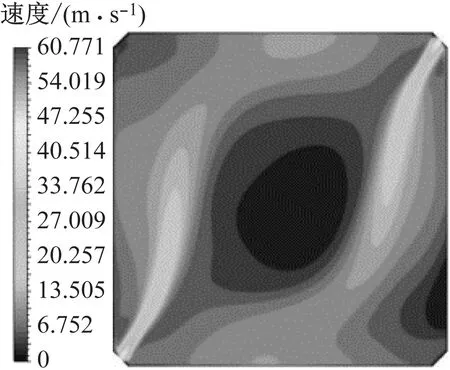
(a) CA角开启

(b) CBAD角全开图7 对角启动的速度场Fig.7 Velocity field of diagonal startup mode

3.1 速度场

图8给出了BMCR工况下不同启动方式P1截面的速度场。从图8可以看出，三者在该截面上的速度分布规律大体一致，高速区大都分布在两侧的近壁面处，越靠近炉膛中心，速度越低。这一分布规律同样适用于图9中P3截面和图10中P4截面的速度场，由4个角喷出的煤粉气流相互撞击，气流沿顺时针旋转形成切圆，靠近切圆中心是一片低速区，越往四周速度越高。经对比发现，图8(b)和图8(c)中的速度场尽管在主燃区有所偏斜，但相较图8(a)中的速度场更加规则，随着SOFA的喷入，气流偏斜明显减小。

(a) 同时启动

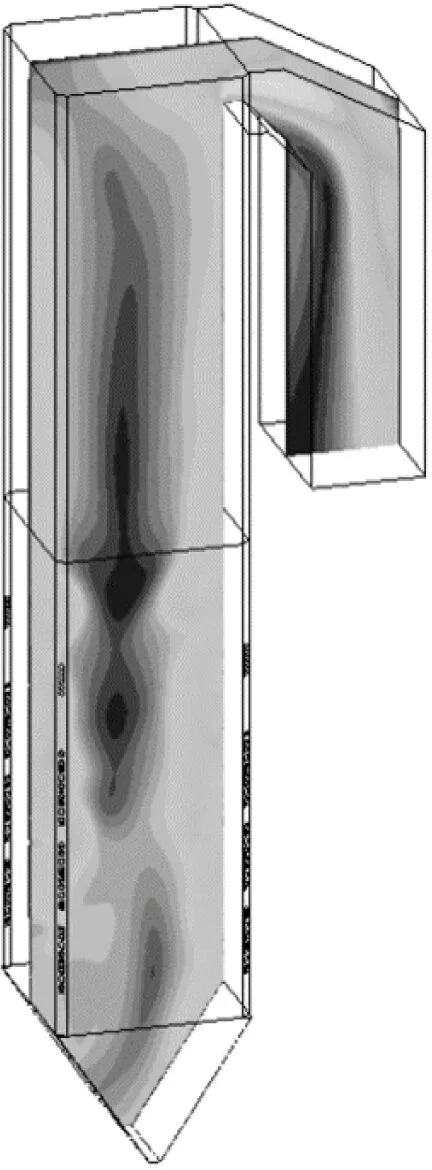
(b) 对角启动

(c) 顺序启动图8 不同启动方式下P1截面的速度场Fig.8 Velocity field of section P1 under different startup modes

(a) 同时启动

(b) 对角启动

(c) 顺序启动图9 不同启动方式下P3截面的速度场Fig.9 Velocity field of section P3 under different startup modes

(b) 对角启动

(c) 顺序启动图10 不同启动方式下P4截面的速度场Fig.10 Velocity field of section P4 under different startup modes

同理，图9(a)和图10(a)中形成的切圆位置产生了明显的偏移，切圆更加近似于椭圆，而当采用顺序启动或对角启动时，虽然切圆中心位置仍存在一定程度的偏斜，但与同时启动方式相比均向该截面中心处靠近，且切圆的圆度有所改善。为了更加直观地把握炉内上游区域的速度分布，图11给出了不同启动方式下L1～L5上的速度分布。由于炉内的湍流脉动较为强烈，其非线性流动导致冷灰斗区域形成了不对称的涡旋，而下部燃烧器区域受此影响，不同启动方式下L1上的速度分布均呈现出较强的不对称性。而在中部燃烧器附近的高度，由于该区域的燃烧最为剧烈，受上游邻角气流的冲击，气流偏斜较为严重，相比之下，当采用顺序启动和对角启动时，L2上的速度分布对称性有所改善，低速区更加靠近炉膛中心，随着SOFA的喷入，由于其速度高、风量大，气流刚性有所提高，当到达炉膛出口时，不同启动方式下的速度分布偏斜均明显减缓，但从图11(d)和图11(e)可以看出，采用顺序启动和对角启动时，速度沿炉膛宽度方向的分布明显更加对称，切圆也几乎位于出口截面的中心。

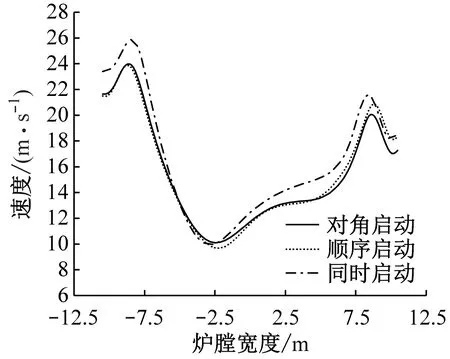
(a) L1

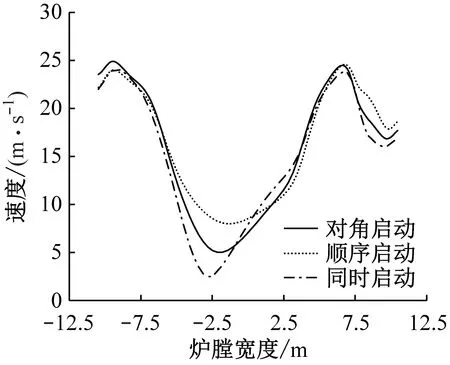
(b) L2

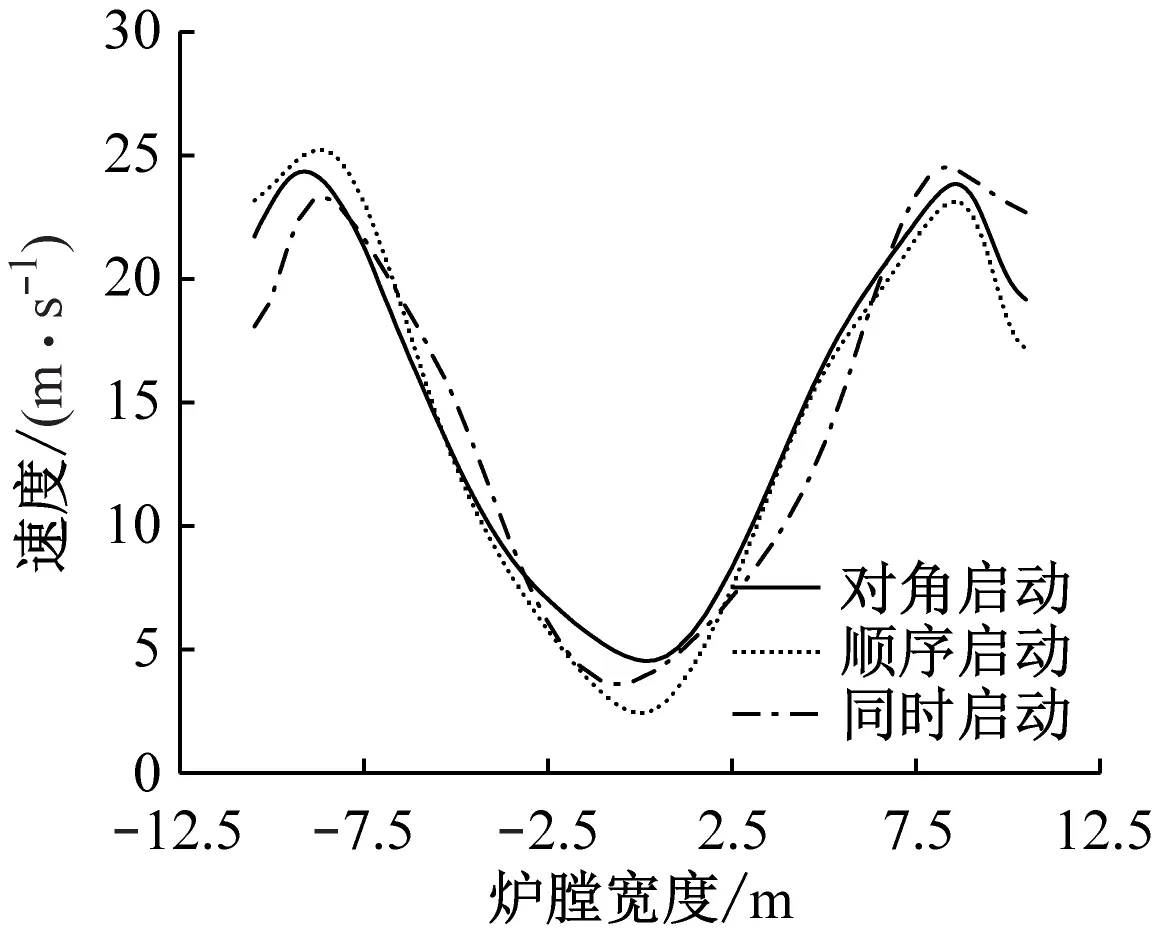
(c) L3

(d) L4

(e) L5图11 不同启动方式下L1～L5上的速度分布Fig.11 Velocity distribution along line L1～L5 under different startup modes

由于炉内的非线性流动，当4个角的喷嘴同时启动时，形成的空气动力场稳定性较差，切圆位置易发生较严重的偏斜，从而引起速度分布的不对称。当采用顺序启动时，首先开启的一个角的喷嘴(本文研究条件下首先开启的是C角)喷出的煤粉气流能够形成较为稳定的初始流场，紧接着当第2个角的喷嘴开启后，C、B两角喷出的煤粉气流在相互作用下同样能够形成较为稳定的流场，随着剩余2个角的喷嘴依次开启，所形成的流场稳定性依次略有降低，但仍优于四角同时启动形成的流场。图12为在对角启动下，首先开启的一组对角上(即C角和A角)的燃烧器喷出的气流在炉膛对角纵向截面上形成的流场，由于其本身的非线性特性，该流场还是会出现一定程度上的偏斜，但总体上较为对称，以此作为初始流场继续开启另外一组对角上的喷嘴，最终形成的流场整体对称性较同时启动有所提升。由于炉内的高雷诺数，非线性流动通常处于混沌状态，初始状态的不同以及运动具有的扩散性[16]使得不同启动方式所对应相空间中两点间的距离随着迭代时间的推移逐渐增大，当达到模态转换的条件时，其中一个点便会进入另一种运动模态继续进行螺旋发散运动，导致两点的运行轨道完全不同，从而呈现出对初值的依赖特性。总之，燃烧器的开启顺序在一定程度上决定了炉内流动初始流场的形成，进而对终态流场产生影响。本文旨在比较3种启动方式下的流场与温度场以及三者在炉膛出口处热偏差现象方面的异同，有关炉内初值依赖特性更深层次的理论分析有待今后进一步研究。

图12 C角和A角喷出的气流在对角纵向截面上的流场Fig.12 Flow field of the airflow ejected from angle C andA on the diagonal longitudinal section

3.2 温度场

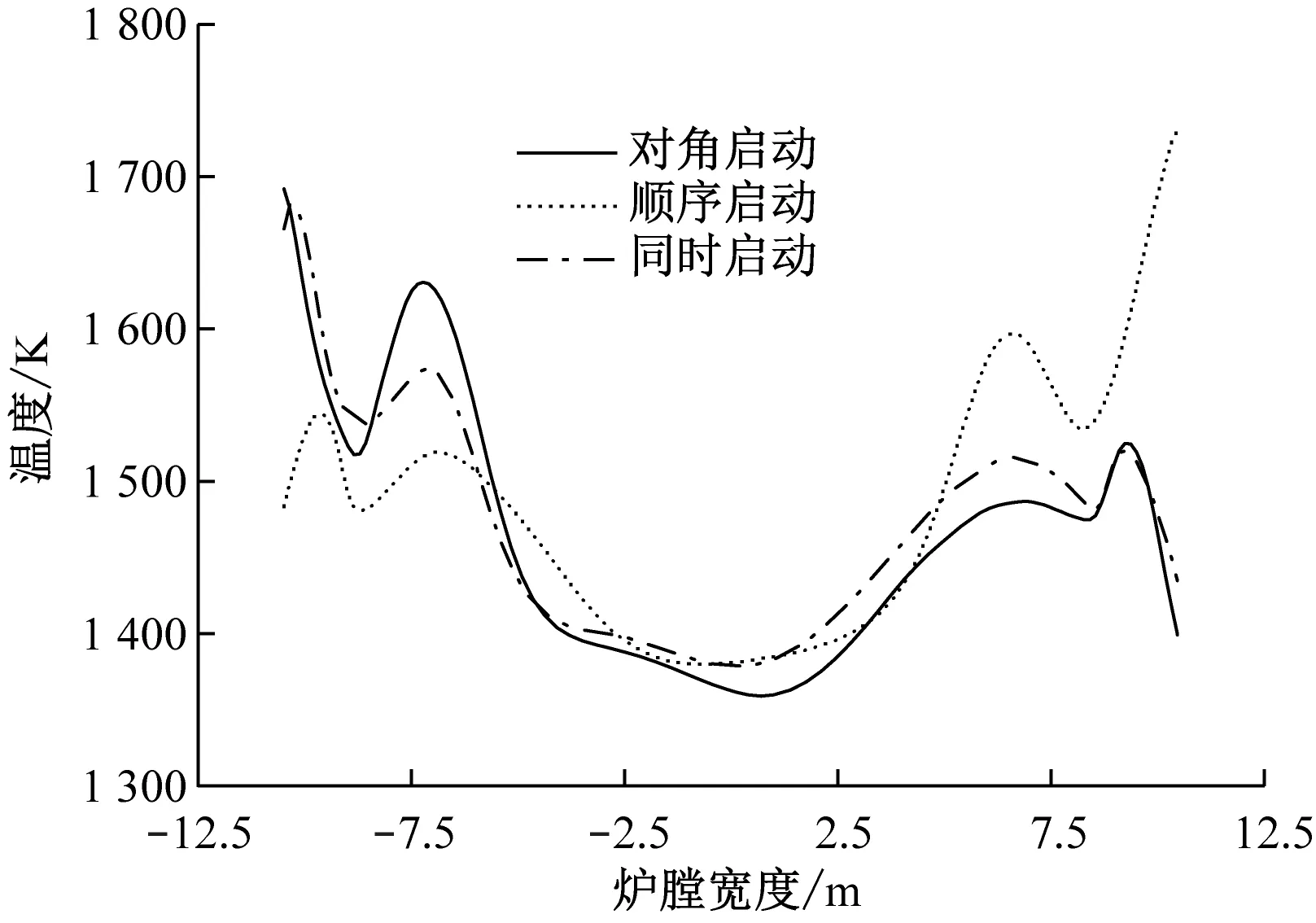
图13给出了BMCR工况下不同启动方式在P1截面上的温度分布。从图13可以看出，沿炉膛高度方向，冷灰斗区域的温度最低，到了主燃区，煤粉与空气充分混合、剧烈燃烧从而放出大量热量，且高温区大都集中在燃烧器附近，由于该锅炉采用了深度空气分级技术，到了上部燃烧器附近，氧气含量的不足导致该区域整体温度略有降低，随着SOFA的喷入，过量空气系数提高，部分未燃尽的焦炭再次燃烧释放热量，使得整体温度再次升高。从图13(b)和图13(c)可以看出，采用顺序启动和对角启动获得的纵向截面温度场在上游区域的偏斜相较同时启动有所减缓。图14和图15分别给出了不同启动方式下P3截面和P4截面的温度场。与图9和图10中的速度场相对应，顺序启动和对角启动的热态切圆圆度更高，且切圆位置更加向截面中心靠拢。从图16可以看出，炉膛出口截面上热态切圆的位置均较为居中，由于切圆中心区域仍存在部分未燃尽的碳颗粒，导致出口截面的中间区域温度较低，这与文献[5]中的结果较为一致。图17给出了不同启动方式下L2～L5上的温度分布。从图17可以看出，由于主燃区流场偏斜较为严重，不同启动方式下L2上的温度分布均呈现出不同程度的非对称性，尤其在同时启动方式下，其低温区严重偏离截面中心；到达还原区之后，受气流刚性增加的影响，L4上温度分布偏斜相对减小，但很明显可以看出当采用顺序启动和对角启动时，L4上的温度分布对称性更优。从图17(d)可以看出，不同启动方式下L5上的温度分布规律基本一致，高温区集中在左右两侧，中间是一片低温区，且右侧高温区的峰值均大于左侧，但顺序启动和对角启动时L5上左右两侧高温区的峰值差别明显更小，这也从侧面说明与传统的同时启动方式相比，顺序启动和对角启动时炉膛出口截面的热偏差更小。

(a) 同时启动

(b) 对角启动

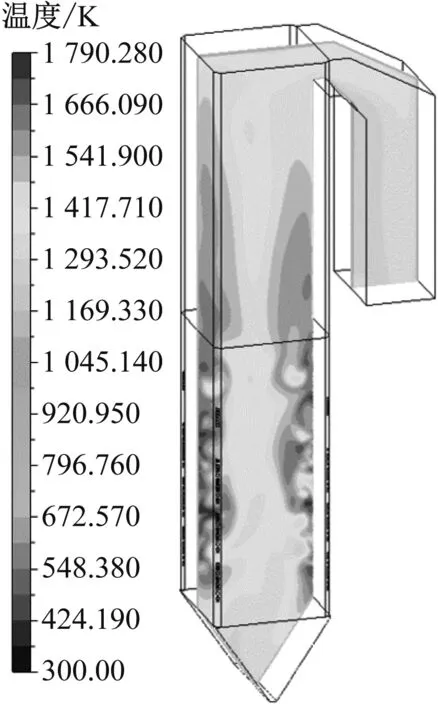
(c) 顺序启动图13 不同启动方式下P1截面的温度场Fig.13 Temperature field of section P1 under different startup modes

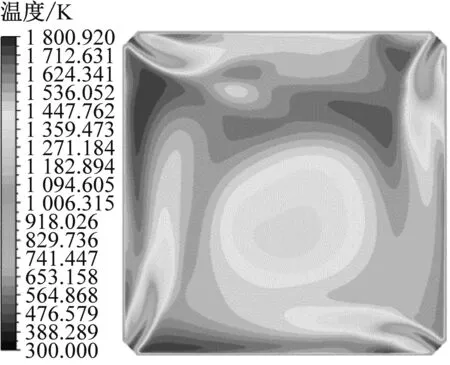
(a) 同时启动

(b) 对角启动

(c) 顺序启动图14 不同启动方式下P3截面的温度场Fig.14 Temperature field of section P3 under different startup modes

(a) 同时启动

(b) 对角启动

(c) 顺序启动图15 不同启动方式下P4截面的温度场Fig.15 Temperature field of section P4 under different startup modes

(a) 同时启动

(b) 对角启动

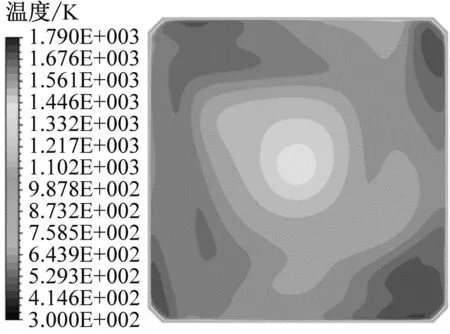
(c) 顺序启动图16 不同启动方式下P6截面的温度场Fig.16 Temperature field of section P6 under different startup modes

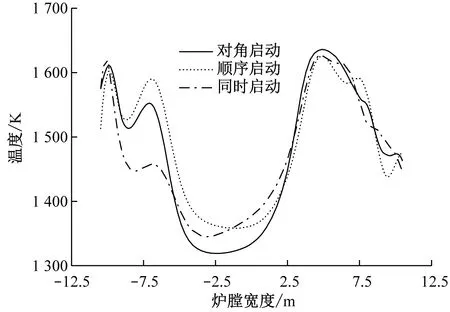
(a) L2

(b) L3

(c) L4

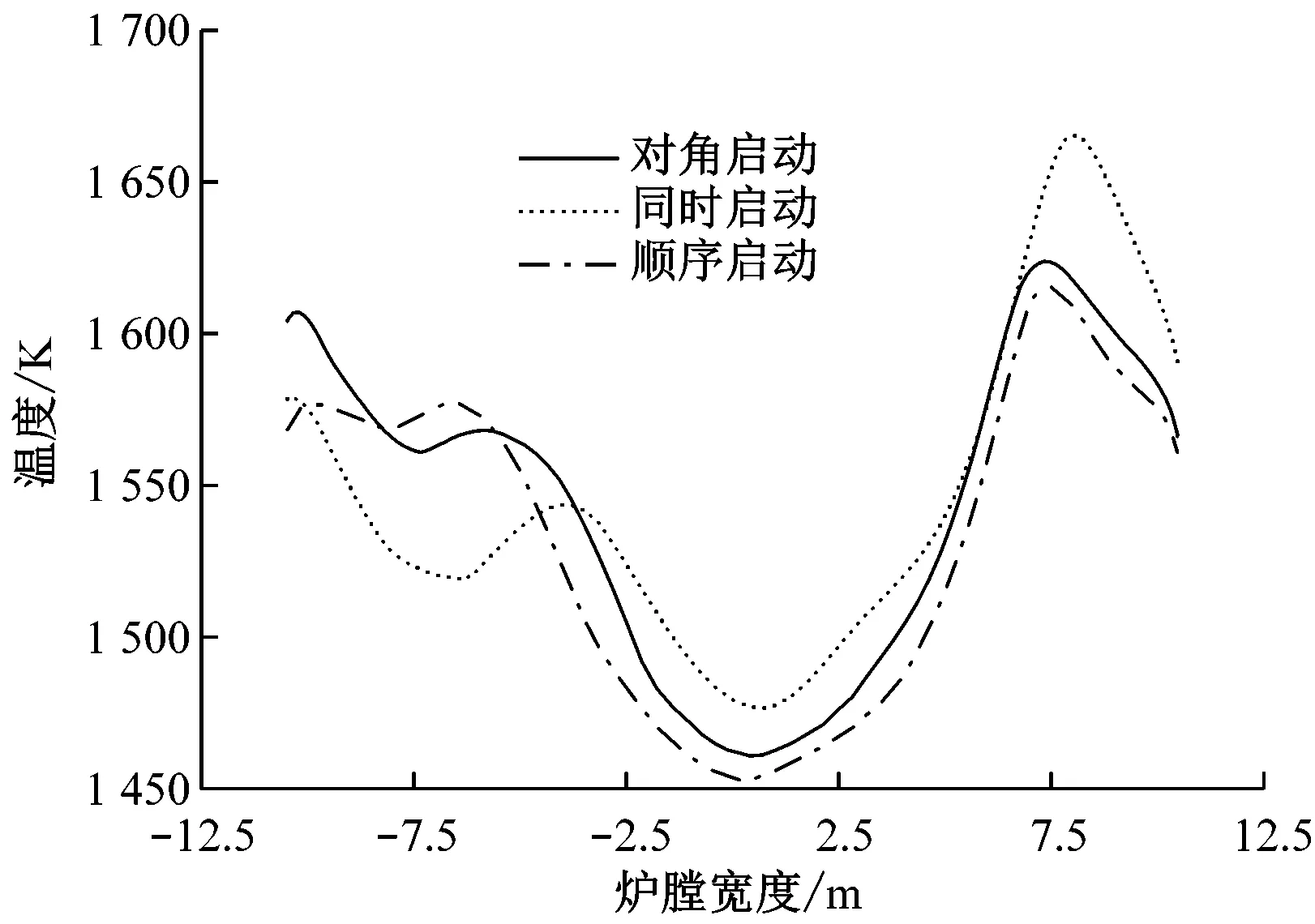
(d) L5图17 不同启动方式下L2～L5上的温度分布Fig.17 Temperature distribution along line L2～L5 under different startup modes

综上所述，不同启动方式下的流场和温度场整体规律基本一致，且由于物理问题本身的非线性特性，都在对称的边界条件下获得了不同程度的非对称结果(包括速度场和温度场)。然而，不同的启动方式产生了不同的初始流场，导致三者终态流场不同，而炉内的流场又在很大程度上会影响其温度分布，最终导致不同启动方式下的温度场也有所差异。

3.3 速度和温度偏差的定量分析

为了对所研究截面左右两侧(见图18)速度和温度分布的偏差情况进行定量分析，分别引入速度分布不均匀系数和温度偏差系数。

图18 截面左右侧Fig.18 The left side and right side of cross section

3.3.1 速度分布不均匀系数

用速度分布不均匀系数M来反映炉内各截面左右两侧烟气速度的偏差程度：

(6)

(7)

表5给出了各截面烟气的速度分布不均匀系数。从表5可以看出，无论采用何种启动方式，主燃区截面的速度分布不均匀系数相对较大，随着SOFA的喷入，速度分布不均匀系数均有所减小，这与上文炉内速度场的变化规律较为一致；而到了炉膛出口截面处，可能是由于随着炉膛高度的增加，每一层的速度偏差持续增大，速度分布不均匀系数有所反弹。与同时启动相比，无论着眼于哪层截面，采用顺序启动和对角启动所得的速度分布不均匀系数均有所减小，这也说明采用这两种启动方式使得炉膛上游区域烟气速度的整体分布更加对称。

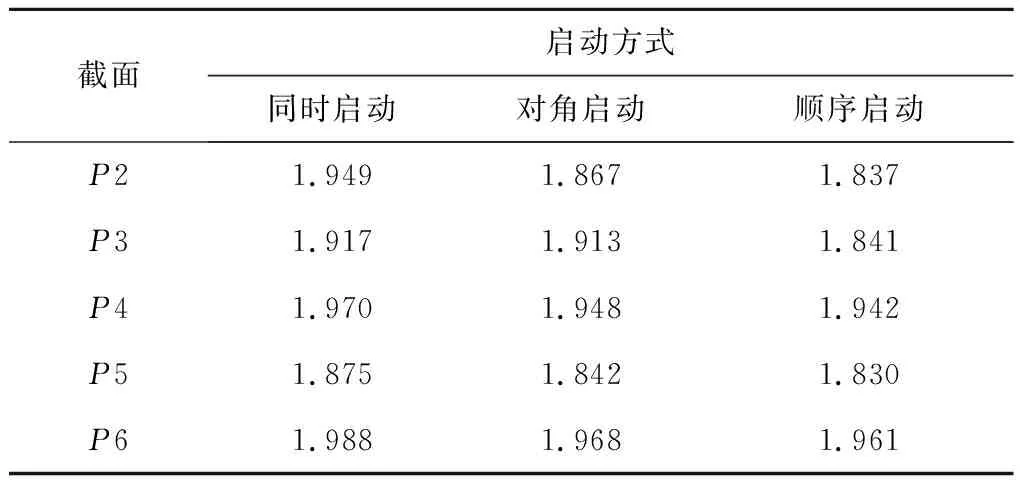
表5 各截面速度分布不均匀系数Tab.5 Uneven coefficient of velocity distribution of each section

3.3.2 温度偏差系数

用温度偏差系数DT来表征炉膛各截面上烟气温度的偏差程度，表示截面左右两侧烟气平均温度之比：

(8)

式中：Tmean-L和Tmean-R分别为各截面左侧和右侧的烟气平均温度。

表6给出了各截面烟气的温度偏差系数。由表6可知，无论采用何种启动方式，主燃区的温度偏差系数较大，因为该区域的燃烧最剧烈；到了还原区，由于气流刚性的提升，温度偏差系数有所减小，到达炉膛出口截面后，温度偏差系数进一步减小。与同时启动相比，采用顺序启动和对角启动所得各层截面的温度偏差系数均有所减小，经计算，采用顺序启动和对角启动时炉膛出口截面左右两侧烟气平均温度偏差由原先的44 K分别降至15 K和20 K。

表6 各截面温度偏差系数Tab.6 Temperature deviation coefficient of each section

4 结 论

(1) 无论采用何种启动方式，由于物理问题本身的非线性特性，在对称的结构和边界条件下均获得了非对称的流场和温度场。

(2) 由于非线性问题具有初值依赖特性，不同的启动方式使得炉内产生了不同的初始流场，进而影响了终态流场的形成，相较于传统的四角同时启动方式，采用顺序启动和对角启动时得到的炉内流场偏斜有所减缓。

(3) 由于炉内的流场很大程度上会影响其温度分布，采用顺序启动和对角启动时能够获得对称性更好的温度场，因而在一定程度上有效减小了炉膛出口处的热偏差。