低海水温度模式下核电厂重要厂用水系统运行优化研究

邢晓峰， 张正楼， 刘林保

(1．上海核工程研究设计院有限公司，上海 200233； 2．辽宁红沿河核电有限公司，辽宁大连 116319)

核电厂重要厂用水系统(SEC)主要是把设备冷却水系统(RRI)的热负荷传导至最终热阱——海水中，SEC/RRI系统为核安全3级。上游用户对RRI水温的限值要求为：主泵热屏及轴承润滑、核岛厂房冷冻水系统(DEG)、电气厂房冷冻水系统(DEL)等要求RRI供水温度≥15 ℃。设计冷水供水温度过低一方面会对主泵密封产生因骤冷导致的热冲击效应，另一方面会直接导致DEG/DEL停运，还可能导致相关设备与管路结冰、冰絮或表面结露等不利影响。

某核电厂采用热水回流掺混来提升供水温度，回流点位于A/B各列2台SEC泵吸水管道之间的进水母管上。机组运行验证了单序列各自运行时，热水回流档位可根据海水温度进行自动控制，使温度满足要求。然而运行中发现，1列循环水过滤系统(CFI，对应取水流道)供2列SEC/RRI运行时，热水回流档位自动控制系统无法执行此复杂工况。另外，两泵切换时因运行特殊要求需先切换至高排水档位(冬III档)再回归切换前档位运行，此时瞬态过程中也存在温度低于限值的情况。刘翠波等[1]针对重要厂用水系统设计供水温度对冷链换热器热工设计的影响进行研究分析。杨廷等[2]对低温厂址条件下设备冷却水换热器热负荷分区运行进行了研究，为热负荷的运行调整提供了参考。闫昊等[3-6]基于Flowmaster、GT Pro等技术对流体系统的热工水力特性进行了分析，为建模仿真提供了参考。

笔者基于数学建模方法建立系统阻力系数超定线性方程组，并采用最小二乘法寻求最优解，预测系统水力特性，探求海水温度与系统供水温度的关系，给出运行调节优化措施。研究成果对于核电厂重要厂用水系统稳定运行有着重要意义，计算方法可供类似系统热工水力计算参考。

1 数值计算与仿真建模

1.1 系统阻力模型构建

传统水力计算结果与实际运行参数存在偏差，因此基于实际调试数据来研究构建数值模型。为节约计算时间，对系统阻力模型进行简化，采用阻力元件替代系统中的复杂部件。分别对系统A列、B列建立图1所示的简化模型。根据压力平衡原则假定系统阻力与损失的线性关系可以得到方程组(1)。

图1 系统阻力计算简化模型Fig.1 Simplified model of system resistance

(1)

其中，K1～K14为阻力系数；qV,ij1、qV,ij2为各热水回流档位对应下的泵供水体积流量，m3/s；qV,ij为各热水回流档位下的排水体积流量，m3/s；Hij2、Hij3为取水、排水流道水位，m；d1～d15为供水系统管道内径，m；g为重力加速度，取9.81 m/s2；ΔHij为泵的扬程，m，可根据重要厂用水泵性能曲线以及流量值推导求得；hij1～hij5为管道沿程水头损失，m，可根据阻力计算[7]推求；h换ij为换热器局部水头损失，m；下标i=3～14分别对应各热水回流档位，j=1～2分别对应每个系列的2台泵。

因此上述线性方程组包含48个方程，14个未知数。可见该线性方程组的系数矩阵秩大于未知数个数，方程组无唯一解，说明系统回路水头损失与阻力系数非一一对应关系。考虑一定的容许偏差，采用最小二乘法求解上述方程，得到一组最优解，使得流量偏差与实际偏差控制在允许范围内。

1.2 仿真建模

Flowmaster软件[8]是一款流体系统设计与仿真软件，能够对不可压缩流体、可压缩流体、液压系统进行分析和模拟，计算流体系统的流量、压力和温度分布等，并能够模拟稳态、瞬态过程。目前，该软件被广泛应用于管网系统热工水力特性分析中。

结合软件特点及系统各部件情况进行建模，系统各部件采取的元器件如下：取水/排水流道采用定高度水箱，输入条件为水位以及取水/排水管道直径；重要厂用水泵的输入条件包括重要厂用水泵的性能曲线、功率、额定扬程、额定流量和额定转速；阀门开度参数可以在参数表中直接输入，也可以通过控制器来设置。对于SEC/RRI换热器，本文热工水力分析重点关注水头损失和热量传递，根据经验采用Flowmaster软件中的Heater-Cooler模型模拟SEC/RRI换热器，输入条件包括阻力系数和热负荷等。Flowmaster中管道阻力模型包括Colebrook-White模型、Hazen-Williams模型和Fixed Friction模型，根据经验工业水行业中常采用Hazen-Williams模型，输入条件为阻力系数。考虑到系统中包含管件、孔板等元件，在系统中补充阻力元器件替代。

2 计算方法与模型可靠性验证

式(1)的每个方程可以转化为K1x1k+K2x2k+K3x3k+K4x4k+K5x5k+K6x6k+K7x7k+K8x8k+K9x9k+K10x10k+K11x11k+K12x12k+K13x13k+K14x14k=Yk。其中，x1k～x14 k为动力水头，为已知量，分别对应方程中K1～K14的乘数，Yk为总水头，为已知量，根据现场实际单泵运行调试数据，基于最小二乘法计算寻优得到一组最优解。图2和图3分别给出了A列、B列阻力元件水头损失计算值与调试值的对比。从图2和图3可以看出，水头损失计算值与调试值较为吻合，2列仅个别点阻力残差最大在2.0 m(误差6.7%)，其余绝大部分阻力残差在±1.0 m(误差5%)以内,精度较高。综上所述，本文模型简化计算方法可信可靠。

图2 阻力计算值与调试值的比较(A列)Fig.2 Resistance comparison of calculated results and experimental data of train A

图3 阻力计算值与调试值的比较(B列)Fig.3 Resistance comparison of calculated results and experimental data of train B

基于阻力模型最优解，建立数值仿真模型，将单泵运行工况计算值与调试值进行对比，供水体积流量、回水体积流量、排水体积流量与调试值均吻合良好。图4给出了SEC001PO泵、SEC003PO泵系统体积流量计算值与调试值的对比，可以看出二者总体趋势一致，误差小于5%。结果表明，所采取的数学模型以及数值仿真模型计算方法得当,体积流量计算值与实际情况吻合较好，验证了其可靠性，可用于组合工况热工特性模拟。

(a) SEC001PO泵

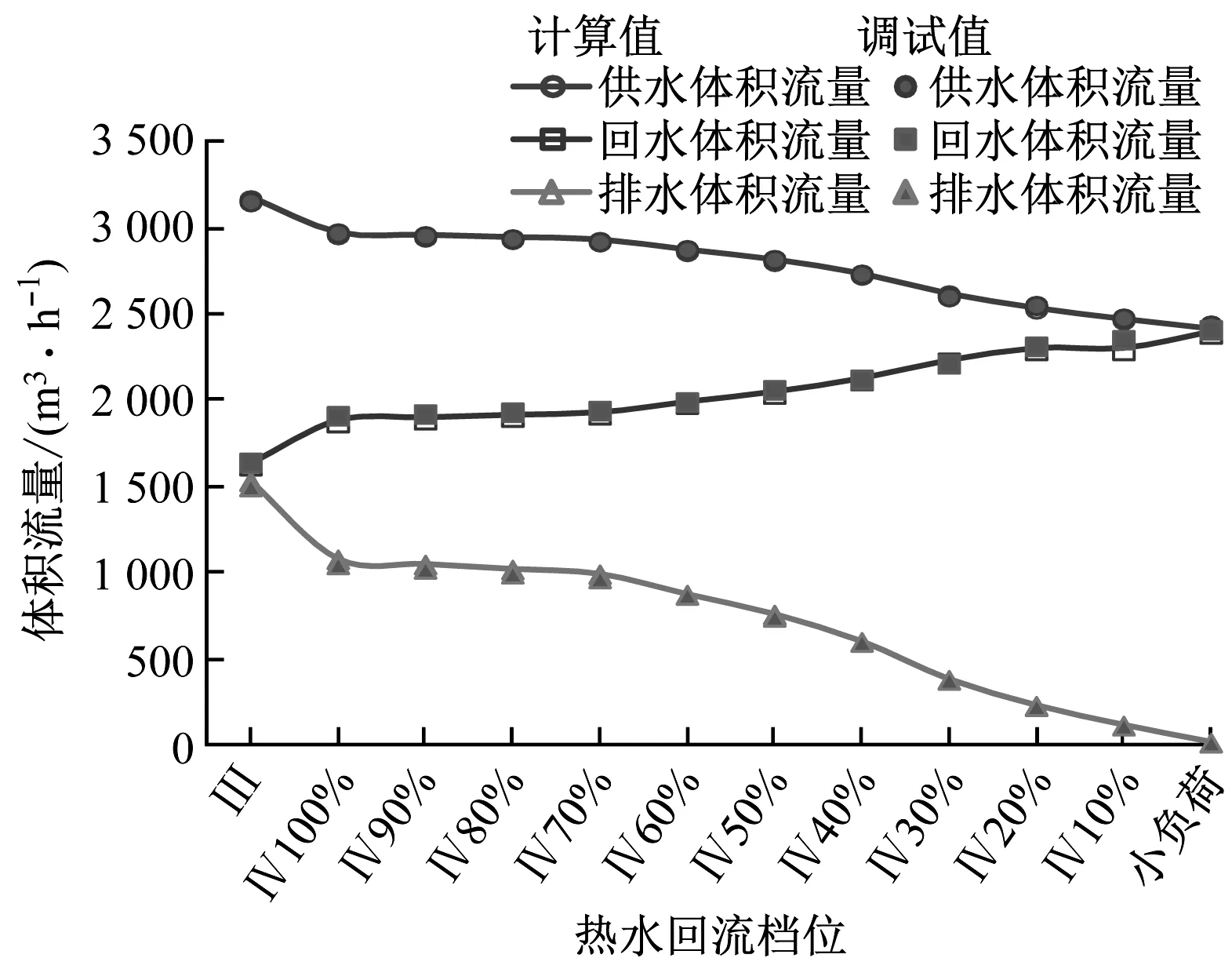
(b) SEC003PO泵图4 系统体积流量计算结果Fig.4 Calculated results of system volume flowrate

3 基于热力特性的稳态运行优化

针对运行中发现的一列流道供应两列SEC供水温度低于限值问题，分析认为，根据水流流动方向，回水优先流向CFI停运列对应的SEC列，会导致CFI运行列对应的SEC列所取的热水回流减少，甚至无热水回流，从而导致该列运行温度下降。基于此，可通过热水回流档位组合，实现热水回流分配。图5给出了3种典型热负荷组合工况[9]下运行热水回流档位组合温度范围图。3种典型热负荷组合如下：热负荷组合1，A列、B列热负荷相同，均为19.925 MW；热负荷组合2，A列热负荷为11.85 MW、B列热负荷为28 MW；热负荷组合3，A列热负荷为3.2 MW、B列热负荷为36.65 MW。B列CFI供应两列SEC。由图5可知，随着海水温度的升高，A列回水温度和B列回水温度均线性升高，当海水温度高于6 ℃时，A列回水温度为35.7 ℃，此时需要调整热水回流档位组合，降低A列回水温度。当海水在极端最低温度-2.5 ℃时，B列回水温度为18.7 ℃，A列回水温度为27.2 ℃，满足温度限值要求，说明了通过热水回流档位组合调整温度的可行性。从图5还可以看出，在总热负荷一定的情况下，随着B列分担热负荷的增加，A列回水温度出现小幅降低，B列回水温度大幅升高，两列回水温度朝着接近趋势发展，说明CFI运行列对应的SEC列分担热负荷比例越大，越有利于优化两列回水温度。

图5 典型热水回流档位组合海水温度与回水温度关系图Fig.5 Relationship between seawater temperature and backflow temperature

表1给出了较不利工况即A列热负荷为3.2 MW、B列热负荷为10.85 MW下，热水回流档位组合情况下对应适用的自然海水温度。可以看出海水温度为12 ℃以上时能够满足要求，因此分析重点考虑的海水温度范围为-2.5～12 ℃。计算结果表明，海水极端最低温度为-2.5 ℃时，通过设置A列IV30%热水回流档位、B列IV10%热水回流档位或小负荷安全档组合，或者 A列、B列均为IV20%热水回流档位组合即可满足要求，同时发现可以组合的热水回流档位随着海水温度的升高而增加。这也验证了运行优化方案的可行性。

表1 热水回流档位组合与海水温度关系表Tab.1 Relationship between combination and seawater temperature ℃

4 基于热力特性的瞬态运行优化

针对同列两泵切换中瞬态过程温度低于限值的情况，利用验证后的Flowmaster模型，对系统热力特性的单系列切换瞬态进行仿真计算，A列热负荷为3.2 MW，A列换档瞬态过程为：初始时刻位于IV10%热水回流档位运行，其后切换冬III档运行，再恢复IV10%热水回流档位。图6给出了正常运行切换工况、优化运行切换工况(提升初始温度)以及优化运行切换工况-增加切换时间3种条件下瞬态温度与时间的关系曲线。从图6可以看出，正常运行切换工况下热水回流档位切换瞬态过程中，温度迅速从22.8 ℃降低至10.7 ℃，恢复热水回流档位后温度逐步提升，重现了机组实际运行过程中出现的切换过程不满足要求的情况。基于此，提出结合冬季热水回流档位提升系统运行温度，利用温度裕量进行缓冲，降低切换瞬态过程中的低温影响的运行优化方案。由图6还可知，热水回流档位切换瞬态过程中，趋势与正常运行切换工况过程一致，系统初始温度为30 ℃，瞬态过程中最低温度为15.0 ℃，高于正常运行切换工况下的最低温度，说明该优化方案可行。同时，瞬态过程恢复至初始运行温度大约需要10 000 s，这主要是由于冬III档引入较多环境冷海水，恢复IV10%后逐步循环加热至平衡，这也说明了可以通过调节优化逐步将系统温度调整至设定的初始温度。当切换时间分别为166 s和266 s时，对应的瞬态最低温度为15 ℃和8.3 ℃，说明缩短切换时间可以有效提升系统切换过渡过程温度。

图6 瞬态温度随时间的变化情况Fig.6 Variation of system temperature under transient conditions with time

5 结 论

(1) 结合水力调试数据建立计算模型，设定系统各部分阻力系数为未知量，根据压力平衡原则，建立超定线性方程组，并采用最小二乘法寻求最优解，然后结合Flowmaster软件建立仿真模型，通过对比流量误差，验证了模型的可靠性，说明所用方法能够用于系统的仿真建模计算。

(2) 热工水力计算发现，通过热水回流档位组合优化来实现运行温度符合准则是可行的，可组合档位随海水温度的升高而增加。在热水回流挡位组合一定的情况下，回水温度随着自然海水温度的升高而线性增加。在总热负荷一定的情况下，CFI运行列对应的SEC列分担热负荷比例越大，越有利于优化两列回水温度。

(3) 对切换过渡过程热力特性开展瞬态仿真计算，重现了机组运行过程中出现的瞬态低温情况。提升初始温度或缩短切换时间可有效提升两泵切换过渡过程温度，从而使得RRI供水温度满足运行限值要求。

本研究成果得到了工程实际应用，相关计算方法对于类似系统热工水力计算具有一定的参考价值。