数学期望原理及其应用

郭华毅

(山西药科职业学院，山西 太原 030031)

概率论是研究随机变量统计规律性的一门学科，分布函数全面刻画了其统计规律性。但在实际问题中，分布函数一般难以求得。而且，在很多时候，我们也未必需要知道随机变量的全部信息，而只关心其某些重要特征。数学期望就是刻画随机变量“平均”取值水平的重要数字特征，在理论和实践中都有广泛的应用。

1 数学期望的概念

随机变量x的数学期望，来源于通常平均数的概念，体现了随机变量的平均取值的大小。针对不同的随机变量类型，可分为两种。

1.1 离散型的随机变量的数学期望

设离散型随机变量X的概率分布为P(X=xk)=Pk,k=1,2，Λ

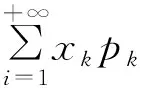
由定义可以看出，数学期望就是随机变量取值关于其概率的加权平均值[1]。

1.2 连续型的随机变量的数学期望

设连续型随机变量X的概率密度函数为f(x)

2 数学期望在实际生活中的应用

2.1 在识别街头骗局中的应用

在日常生活中，我们经常碰到一些街头游戏，比如地摊骰子、猜数赢钱、摸球中奖等。这些游戏普遍上看上去对顾客有利，但很多人却在这些看似有利的游戏中输了不少钱。那这些游戏的奥妙在那里呢，我们不妨以摸球中奖游戏为例分析一下。

游戏规则这样的：有一个袋子里放着6个红球和6个白球，参与者可以“免费”从袋子中摸6个球，兑奖规则如下：6个全红，赢100元；5红1白，赢50元；4红2白，赢20元；3红3白，输100元；2红4白，赢20元；1红5白，赢50元；6个全白，赢100元。

七种情形只有一种是输钱的，其它六种均能赚钱，表面上看这个规则对顾客是非常有利的，但观察下来，参与者却是输多赢少。问题出在那呢？

我们不妨计算一下。任取6个球，取到i个红球和j个白球的概率为：

E(X)=(0.001*100+0.039*50+0.244*20)*2-0.433*100=-28.98(元)

也就是，玩家在这种游戏里每次“平均”都会输掉近29元，也难怪玩的越多，输的越多。

2.2 在投资决策中的应用

在投资中，我们会碰到如何设定最佳投注比例的问题。对于这个问题，1956年约翰·拉里·凯利(John Larry Kelly)在《贝尔系统技术期刊》提出了大名鼎鼎的“凯利公式[3]”，该公式如下

其中，各个参数的意义是

f：应投注的筹码比例

p：获胜的概率

q：失败的概率，即1-p

b：赔率，等于可能的盈利/可能的亏损，也就是盈亏比

这个公式应该怎么应用呢？

假设有一个小游戏，抛硬币赌正反。抛得正面者赢2元，抛得反面者输1元，你有100元，每次下注金额不限，那最优下注方法是什么呢？

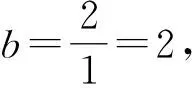
该公式的分子中的bp-q，其含义就是“盈利的数学期望”，原理见表1。

表1 游戏X的胜率、赔率

则盈利的数学期望E(X)=bp-1*q=bp-q

实践中，应用这个公式的前提是bp-q>0，这是因为：

(1) 盈利期望bp-q<0时，赌徒不具备任何优势，会越赌越输，不应该下注(如前面的摸球中奖骗局)。

(2) 盈利期望bp-q=0时，这是个公平游戏，也不应该下注。

(3) 盈利期望bp-q>0时，可以参与，这时候按照凯利公式投注赚钱最快。

2.3 在传染病筛查中的应用

医学上，为了确定某种疾病的传染情况，需要对特定人群进行筛查。假设某地区有N个人，如果我们逐个筛查，就需要进行N次，工作量较大，那么如何减少筛查次数，提高筛查效率呢？

假设阳性反应率为0.04，则平均筛查次数X的数学期望为

显然当K=2,3,4……时，E(X)<1，平均筛查次数小于1，说明分组比不分组好

进一步，可以对E(X)求最值，得出当k=16时E(X)取得最小值，即每组16人最好。

分组人数与阳线反应率a有关，对不同的a值，用上述方法可以计算出不同的最佳分组人数见表2[4]。

表2 不同的值对应的最佳分组人数

2.4 在运动员选拔方面的应用

对于一场重要的体育比赛来说，如何选拔出“最好”的运动员去参赛往往是人们关注的焦点。从数学角度，我们可以通过期望和方差这两个标准去选拔。

比如有甲、乙两名射手，其射击成绩如下，问谁的射击水平更好？

甲射中目标靶的环数X是8、9、10对应的概率分别是0.3、0.1、0.6.

乙射中目标靶的环数Y是8、9、10对应的概率分别是0.2、0.5、0.3.

通过计算E(X)=9.3,E(Y)=9.1

数学期望反应了射击的准确度，E(X)>E(Y)，说明从准确度角度看，甲要优于乙。但是不是一个好的射手，还需要从稳定性方面考察，这可以从均方差来比较。

3 应用数学期望时候需要注意的问题

3.1 不能简单把数学期望等同于均值

我们平时所说的均值通常是算术平均值，即默认每个量出现的概率是一样的；而数学期望中每个变量出现的概率可能不同，因此其含义是加权平均值。

3.2 注意数学期望实现的条件

在投资中，一个正的数学期望意味着这不是赌博，有了参与的可能。但要注意，正的期望值是在大量重复实验条件下才可能出现的“均值”，在有限的实验次数下，实验结果完全可能极度偏离或者长期偏离。如果想获得期望值，必须保证遍历性[5]。遍历性是指统计结果在时间和空间上的统一性，表现为时间均值等于空间均值。

总之，数学期望概念广泛应用用工程技术、经济社会的各个领域。熟练理解和运用这个概念，有助于正确认识客观世界的发展规律，为进一步的决策分析提供依据。