基于流固耦合探究高血压对冠状动脉粥样硬化斑块的影响*

都业鹏，李安宁，侯占举，刘剑，张丽丽△

(1.齐鲁工业大学(山东省科学院)机械工程学部，济南 250353；2.山东大学齐鲁医院放射科，济南 250012；3.山东大学控制科学与工程学院， 济南 250061)

引言

冠状动脉疾病严重影响人们的健康生活[1]。其形成和发展与冠状动脉内皮细胞炎症密切相关，而炎症的发生受血液流动环境的影响较大。 当前，许多老年人患有冠状动脉粥样硬化的同时，经常伴有高血压等慢性病。高血压会改变人体循环系统中血液流动条件，影响冠脉粥样硬化斑块的增生[2-3]。因此，研究高血压对冠状动脉内血流动力学的影响，清晰了解内皮细胞炎症的成因、发展及最终导致冠状动脉疾病的过程，对探究冠脉粥样硬化的致病机理具有重要意义。

国内外学者对冠状动脉血流动力学开展了大量研究，Buradi 等[4]认为壁面剪切力(wall shear stress，WSS)和颗粒相对停留时间(relative residence time，RRT)对冠脉疾病的发生发展有着重要影响：较低的WSS区域会诱发斑块的形成和发展，较高的WSS区域会促使斑块发生破裂，进而形成血栓堵塞血管[4-7]；高RRT值与扰动血流增加和WSS降低相关，较高的RRT会增加血小板和白细胞粘附到内皮的可能性，导致平滑肌细胞增殖，RRT值大于8 Pa-1区域被认为是诱发冠脉疾病位置[4]。早期主要通过传统计算流体力学方法(computational fluid dynamics， CFD)研究血液的流动，只考虑了血液流动而忽视了血管壁收缩作用，随着计算机性能不断提高和CAE软件日益成熟，在血液流动中考虑血管壁收缩已可行，促进流固耦合方法(fluid-structure interaction, FSI)在心血管疾病研究中的应用。Wang等[8]验证了血管脉动性的流固耦合方法比传统计算流体力学方法更能准确描述血流在冠脉中的流动情况。在流固耦合方法应用初期，冠脉血管壁被看作是线弹性材料[9-10]，尽管将血管壁看作线弹性材料的计算结果优于刚性材料，但与真实情况仍存在误差，随着研究不断深入，Mooney-Rivlin超弹性模型被认为是较贴近真实血管特性的模型[11-13]，在工程模拟算例中被广泛采用。基于流固耦合计算方法及弹性材料模型取得的进展，涌现大量血流动力学数值分析算例，集中体现在冠脉形态[4,14-15]、斑块类型[16]、支架植入[17-18]和搭桥[19-20]等方面的研究。研究高血压对冠脉疾病特别是粥样硬化斑块的影响，在临床上需要大量样本数据，难以持续跟踪病患斑块生长变化。本研究从血流动力学角度出发，采用真实患者冠脉CT建立血管模型，考虑血流的脉动性和血管壁的顺应性，设计了基于流固耦合的数值分析仿真实验，开展不同血压下的冠状动脉内血液流动特征模拟研究，获取血压对冠状动脉粥样硬化斑块发展的影响，辅助临床医生对该疾病的诊疗。

1 方法

1.1 控制方程

(1)流体域控制方程

在流体域计算中，控制方程包括连续性方程和动量方程：

∇·v=0

(1)

(2)

(2)固体域控制方程

血管壁控制方程是由牛顿第二定律得出：

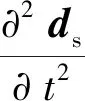
(3)

式中，ρs为血管壁密度，ds为血管壁位移矢量，σs为应力张量。

(3)流固耦合界面控制方程

(4)

式中，n为单位法向矢量；σ为应力；u为速度矢量；d为位移矢量；s和f分别为固体域和流体域。

1.2 材料属性

血液被认为是一种各向同性、不可压缩、均匀的非牛顿流体，具有恒定密度，取ρf为1 060kg/m3[21]。考虑了血液的剪切变稀行为，Carreau模型[22]能很好地拟合，本构方程如下：

(5)

血管壁假设为各向同性、均质的非线性材料。本研究中使用5参数Mooney-Rivlin超弹性模型来表示冠状动脉血管的力学性能[13]。本构方程如下：

(6)

式中，I1和I2是第一和第二应力不变量，c10(-4.02 MPa)、c01(4.321 MPa)、c20(18.401 MPa)、c11(-51.856 MPa)和c02(39.105 MPa)为描述变形的超弹性常数，d(2.434 MPa-1)为不可压缩参数，J为弹性体积比，血管壁密度ρw取1 120 kg/m3。

1.3 冠脉建模

本研究中使用患者真实冠脉CT数据建立冠脉模型。由于左冠脉结构比右冠脉更复杂，且冠脉疾病发生位置大多在左冠脉[23]，故本研究对左冠脉进行建模：

(1)将DICOM 格式保存的CT数据导入Mimics 19.0软件，选取合适阈值范围生成模型，通过区域生长选取左冠脉并生成三维模型。

(2)将生成模型的中心线及轮廓线提取保存并导入至SolidWorks软件，建立血液流域模型。

(3)考虑血液与血管之间的流固耦合作用，建立血管壁模型。对血液流域模型进行抽壳，生成血管壁，取壁厚为0.4 mm。冠脉粥样硬化斑块由手动添加斑块实现。由于冠脉分支对研究区域的血流状态存在影响[24]，本研究模型保留了前降支下游的冠脉分支，所建冠脉模型见图1。

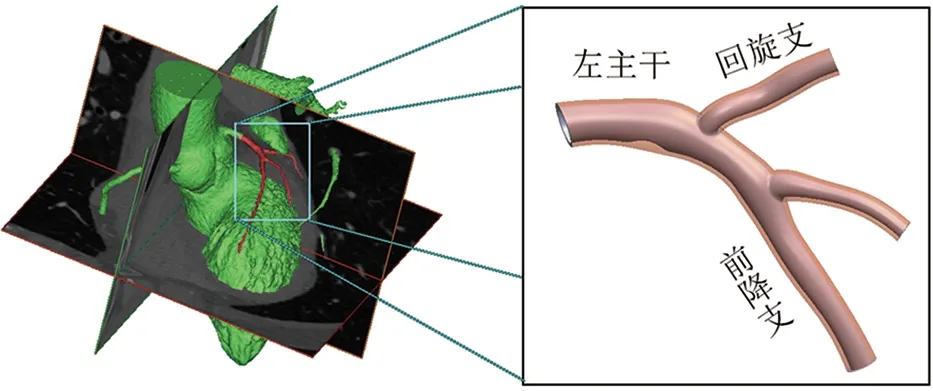
图1 冠状动脉模型Fig.1 The model of coronary artery

1.4 网格划分

在冠脉模型网格划分中，流体域和固体域都采用四面体单元进行离散化，该单元能提高网格形变时的数值收敛性。冠脉模型网格划分见图2，上部分网格是流体域，下部分网格是固体域。

图2 冠脉模型的网格划分Fig.2 Mesh of coronary model

1.5 边界条件

本研究中血液入口速度和正常出口压力来自文献[13]。在Matlab软件中使用傅立叶级数拟合生理脉动流速和压力波形。高血压模型分为轻度、中度和重度高血压。求解过程中，边界条件通过编译UDF函数实现。

入口速度：由图3(a)可知，在正常血压、轻度、中度和重度高血压模型中，入口速度是相同的。

出口压力：由图3(b)可知，黑色线条代表正常血压，红色线条代表轻度高血压，蓝色线条代表中度高血压，绿色线条代表重度高血压。从正常血压至重度高血压，出口边界条件依次提升10 mmHg。

图3 边界条件(a).入口速度; (b).出口压力Fig.3 Boundary conditions(a). inlet velocity; (b). outlet pressure

1.6 数值分析

利用商用计算软件ANSYS Workbench，对冠状动脉模型中的血液流动进行双向流固耦合模拟。任意拉格朗日-欧拉(arbitrary Lagrangian Euler, ALE)方法能保证流体域和固体域的边界和界面在迭代过程中被精准追踪[25]。

本研究对每个冠状动脉模型，都进行了三个心动周期的瞬变流动模拟。为了消除计算初期血流不稳定影响，取最后一个心动周期的结果用于血流动力学分析。设置时间步长等于0.005 s，每个心动周期总步长为160次。在每个时间步内迭代耦合，直到耦合系统残差小于指定的残差[26]。在本研究中，残差设置为10-4。

2 结果与分析

为了方便观察模拟结果，后处理中将正常血压、轻度、中度和重度高血压模型分别被标记为模型#1、#2、#3和#4。速度流线图能反映出血液的流动和分布情况，各冠脉模型在收缩峰值时期(t=1.85 s)的速度流线，见图4。不论正常模型，还是高血压模型，狭窄处速度都会变大，狭窄后斑块位置可清晰观察到涡流的存在，并且该处速度较小。由速度流线云图可知，冠状动脉粥样硬化斑块的存在会使血液流速迅速升高，斑块后方会出现涡流且该处速度较低。随着血压的不断攀升，斑块后方涡流强度增强，低流速区域变长。由于发生涡流和低流速区域促进动脉粥样硬化斑块进展，由此分析，血压升高会促进该区域冠脉疾病发展。

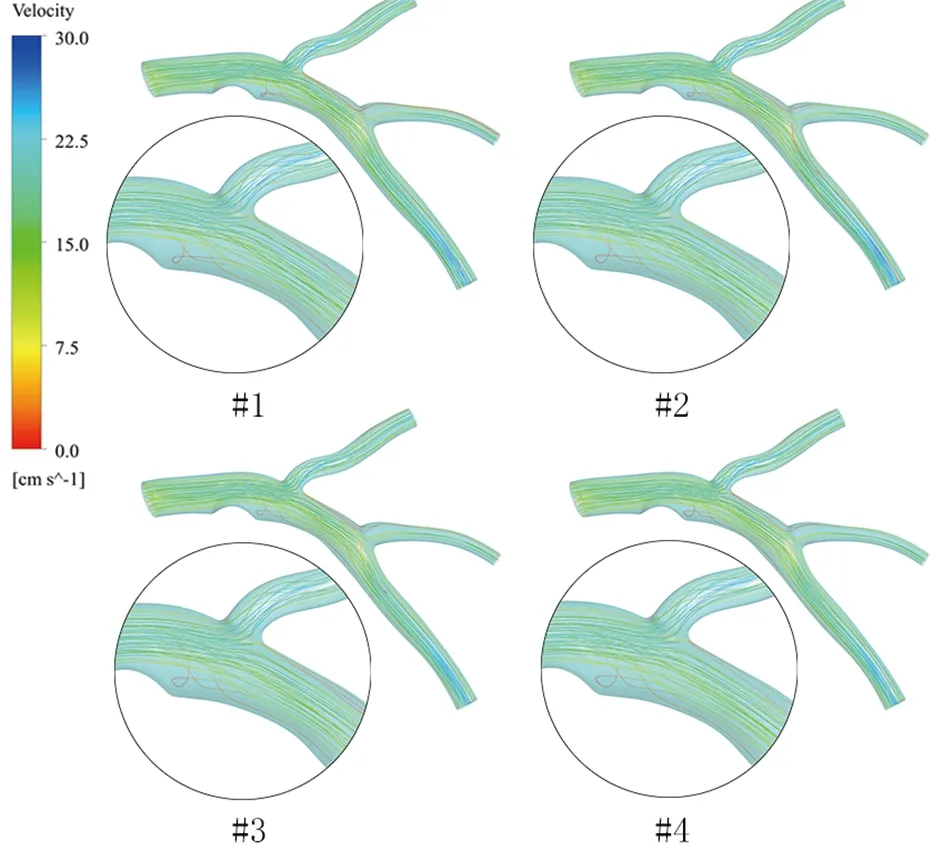
图4 收缩峰值期速度流线分布Fig.4 The distribution of velocity streamline at peak systole

为观察速度分布，建立了截面1和截面2，见图5(a)。各模型在狭窄后的截面速度云图见图5(b)，在模型#1、#2、#3和#4中，截面平均速度分别为4.52、4.44、4.28、4.22 cm/s，最大速度分别为20.76、20.46、19.97、19.73 cm/s，最大速度出现在偏离斑块一侧，从速度最大值至壁面速度呈梯度下降。在回旋支和前降支分叉位置，即截面2处，速度云图见图5(c)，云图上部分代表流入回旋支的速度分布，下部分代表流入前降支的速度。从正常血压到重度高血压模型中，截面平均速度分别为7.39、7.29、6.97、7.00 cm/s，最大速度分别为29.15 、28.75、27.98、27.57 cm/s。最大速度出现位置都出现在回旋支入口处。由于分叉处回旋支血管直径小于前降支直径，回旋支入口速度高于前降支入口速度。

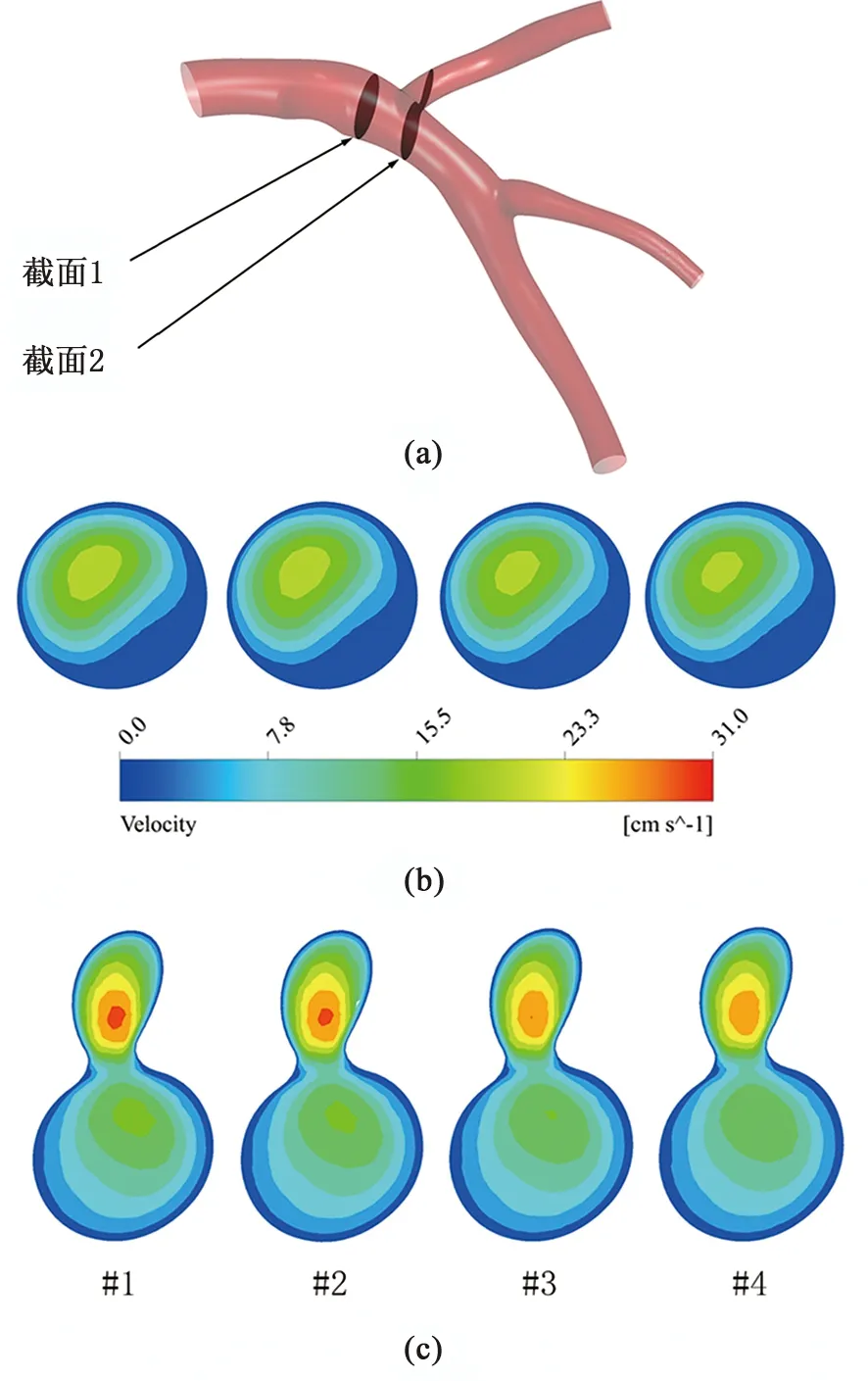
图5 (a).截面位置；(b).狭窄后血管截面速度云图；(c).分叉处血管截面速度云图Fig.5 (a). The position of section; (b). The velocity contour behind plaque; (c). The velocity contour in bifurcation

观察狭窄后截面1处速度分布，轻度、中度和重度高血压模型截面平均速度分别比正常血压模型低1.77%、5.31%、6.64%；截面最大速度比正常血压模型低1.45%、3.81%、4.96%。这表明高血压会造成血流速度减慢。随着血压的不断升高，平均速度和最大速度均不断降低，且速度降低幅度和血压变化呈非线性关系，从模型#2至模型#3的速度降幅较从模型#3至模型#4的大。观察截面2处速度分布云图，模型#1、#2、#3截面平均速度分别比模型#4低1.35%、5.68%、5.28%，最大速度分别低1.37%、4.01%、5.42%，且最大速度出现在回旋支分支中。该处随着血压的不断升高，血流速度依旧降低，截面2处最大速度变化与截面1处相似。然而，从数据观察到中度高血压模型至重度高血压模型，截面2平均速度有所回升，分析其与截面1不同的原因，是该过程中速度下降幅度较小，且速度存在波动造成的。由于随着血压攀升，血液流速降低，而血液承担着运输营养物质和氧气的作用，血液流速降低必然影响血液系统的正常代谢，进而促进冠脉粥样硬化发展。

各模型TAWSS值见图6，由于小于0.4 Pa的区域代表易发生斑块生长，所以图中圆形区域对TAWSS大于0.4 Pa区域进行了透明化处理，只保留了小于0.4 Pa的区域。由图可知，较低的TAWSS发生在狭窄后方和回旋支分叉位置前方，前降支下游分叉血管位置也出现了低TAWSS区域。从模型#1至模型#4，TAWSS小于0.4 Pa的区域面积分别为1.226×10-5、1.232×10-5、1.237×10-5、1.339×10-5m2。模型#2、#3、#4的低TAWSS面积分别比模型#1的高0.5%、0.9%、9.2%。随着血压升高，低TAWSS区域不断增大，且增大幅度在中度高血压至重度高血压过程最高。

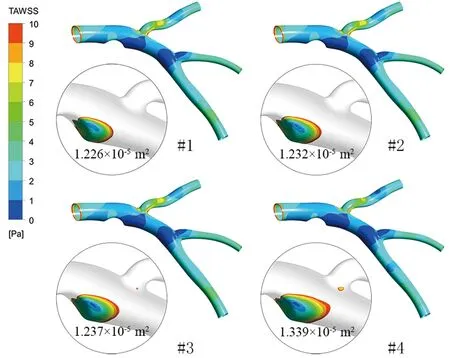
图6 TAWSS小于0.4 Pa区域云图Fig.6 TAWSS contour range less than 0.4 Pa

振荡剪切指数(oscillatory shear index, OSI)可以体现壁面剪切力在时间和空间上的振荡性。较高OSI值区域会诱发动脉粥样硬化斑块发生。正常模型至重度高血压模型，最大OSI分别为0.312、0.331、0.358和0.394,见图7(a)。说明随着血压不断升高，血液振荡会加剧。

图7 (a). 不同模型的OSI最大值；(b). RRT大于8Pa-1区域云图Fig.7 (a). Max OSI of different models;(b). RRT contour range more than 8 Pa-1

RRT能反应粒子在血管壁的停留时间，值越大表示粒子在该区域的运动越缓慢，越容易发生动脉粥样硬化，研究中认为RRT大于8 Pa-1的区域易发生冠脉粥样硬化。RRT大于8 Pa-1区域云图见图7(b)，高RRT发生在斑块后方。从模型#1到模型#4， RRT大于8 Pa-1的面积分别为1.945×10-6、1.958×10-6、1.969×10-6、2.341×10-6m2，且模型#2、#3、#4的高RRT区域面积分别比模型#1的高0.67%、1.23%、20.36%。从中度高血压至重度高血压过程中，高RRT区域面积变化最大。

通过上述分析可知，低TAWSS区域和高RRT区域都是在轻度高血压和中度高血压模型中变化幅度较小，而在重度高血压中极大，说明在重度高血压情况下，冠脉血流会发生严重紊乱，极大地促进了冠状动脉疾病发展。从数值模拟结果可以得出，不论正常模型还是高血压模型，斑块后方和分叉位置都是容易诱发动脉粥样硬化区域，这些区域表现出低TAWSS 、高OSI和高RRT。

3 结论

为研究高血压对冠状动脉斑块的影响，本研究基于血流脉动性和血管壁顺应性，采用流固耦合方法模拟正常血压、轻度、中度和重度高血压条件下，血液在冠状动脉的流动情况。为了保证模拟结论的可靠性，冠状动脉模型通过真实患者冠脉CT数据创建，考虑了冠脉血管中血液的非牛顿特性和血管壁力学特性。研究结果表明，随着血压的不断攀升，血流速度会逐渐降低，但是速度变化与血压变化呈非线性关系，轻度高血压至中度高血压阶段血流速度降低幅度较大。低TAWSS区域和高RRT区域随着血压升高不断增加,且在中度至重度高血压过程中增加幅度最大。仿真结果显示，高血压会加速冠状动脉斑块的发展，已有斑块沿血流方向扩增，新增斑块易发生在血管分叉位置。