化归与转化思想在初中数学解题中的应用
刘玉珍
【摘要】本文简要介绍了化归与转化思想,介绍了化归思想在数学教学中的常见用法.最后,针对初中数学解题教学实践,提出了几点应用化归与转化思想的策略.文中通过列举具体教学案例,望为初中数学教学实践提供参考.
【关键词】化归思想;教学方法;转化思想
化归与转化的思想方法,在数学领域的教育工作和学习过程中,都有着重要的实用意义.可以说,在中学阶段的数学学科教学中,离不开对化归与转化思想的运用.
目前部分初中数学教师对化归与转化思想有了一定的理解,并在教学工作中能加以运用.但也有部分教师对化归与转化思想理解程度不高,也没有积极在此方面钻研,导致实际的数学教育工作过于死板,仅能按照教材中给出的方法教育学生解题[1-2].这样的教育方式一方面不利于教师开展教学活动,提升自身教学能力.
另一方面不能让学生由被动学习转变为自主灵活地思考解答方法,不利于学生数学学科综合素养的提升.所以,未来初中数学教育应重视对化归与转化思想的研究,更好的培养学生的数学思想,提升其独立解答问题的能力[3].
1 化归与转化思想的相关概述
化归与转化思想,实质上是一种面对不同类型的问题时,采取某一种的转化的方法,让解题思路更加清晰,让解题过程更加简便的思想方法.
化归与转化的历程,能够让对某一难以解答的问题,或是非常陌生的问题的思考和解答,转变为对便于解答的问题,或是比较熟悉的问题的解答与思考.这样的思想方法在学习过程中的实际运用,将大大提升学生学习效率和效果[4].
数学学科同其他学科对比,可以发现数学学科的教育教学是比较适合运用化归与转化思想的.在讲解陌生的数学题目时,教师可以引导学生将题目转化之前讲解过的题型,将较为繁琐的题目化为便于解答的题型,将第一次遇到感觉较为陌生的题化为已经熟练掌握的题目.
由此可见,在初中数学解题教学中,对化归与转化思想的运用,实质上就是要拉进题目中的已知和要求得的解之间的距离,在解答题目的过程中,使求解系统逐渐贴近于目标系统,使陌生的解题方法逐渐转变为熟悉的解题方法[5].
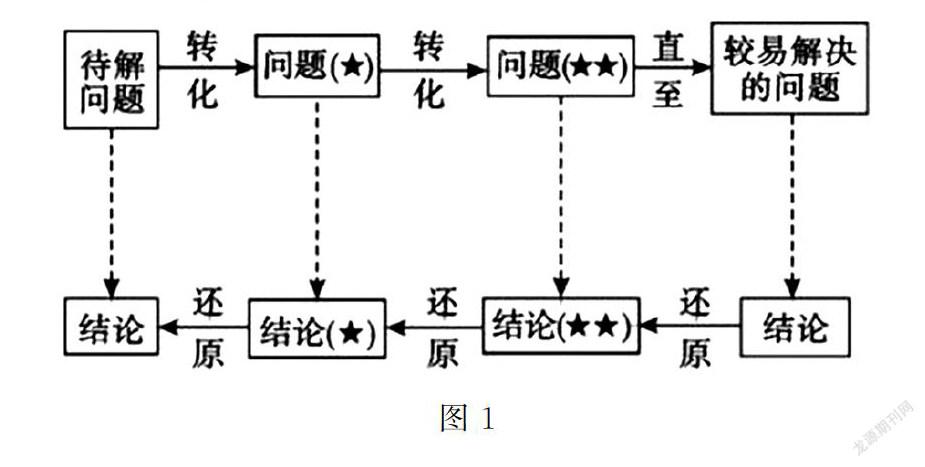
化归与转化思想在教学中的应用方法框架如图1所示.因此在实际开展的数学教学工作中,无论遇到的是繁琐的题目还是简易的题目,解题教学都不能脱离化归转化的思想方法.数学学科内容中的因式分解,三角函数,解析几何,几何变换理念中,都与化归转化思想方法有千丝万缕的关联.
可见,化归思想方法是各种思想方法的根基,是求解问题的基础方法.数学学习中化归的常见方法,包括分和法、等价转化法、不等价转化法、构造法、映射法、特殊化法、递归模式[6].
2 初中数学教学中的化归转化思想应用策略
2.1 教师增强对化归与转化思想原则的认识
2.1.1 化隐性为显性原则
转化与化归思想方法广泛地蕴含于初中数学内容之中.进行教学时必须以数学知识为载体.
例如 讲解三个一元二次方程问题为例.三元一次方程问题的解答,与对一元二次方程、一元二次函数、一元二次不等式的解答思路有共通之处.引导学生掌握相互转化的能力,能够体现出对数与形的转化、判别式与根个数的转化、图像与不等式解集的转化.将学习内容中隐性的关联,转化成学生能直观看到,能更直接学到的显性关联,提升学生对数学知识的记忆与理解能力,更好地将学到的知识运用到对问题的解答中[7].
2.1.2 螺旋上升原则
初中数学教学中运用转化与化归思想方法,并不能像直接教给学生解题公式一样,取得一步到位的直接教学效果.转化与化归思想方法,取得的教学成果需要过程才能体现.在不同的学习阶段进行不同程度的教学,让学生在原有的基础上稳步提升对转化与化归思想方法的认知.所有的教学活动都是具有一定规律的,通常是先一般后特殊,先简单后复杂,先直观后抽象[8].当然对转化与化归思想方法的教学也是从底到高的螺旋上升的.
2.1.3 系統教学原则
转化与化归思想,实际上是一个有机的整体,在数学教学工作中运用转化与化归思想方法,需要将思想方法的整体与具体的教学内容进行融合,在知识中渗透思想,利用思想来提升对数学问题的理解、掌握和解决能力.
2.1.4 学生参与原则
课堂教学活动是以教师为主导,学生为主体的合作学习过程.发挥学生的主体性有利于培养学生的数学核心素养.核心素养的理念最开始是在教学的综合方向提出.核心素养的理念就是针对学生在各学习时期应具备的各方面综合素质,体现了学生个体的综合素质的重要性.
在初中的数学教育中,核心素养具体的表现为学生在数学的学习中得到的综合性学习能力.数学课堂中的教和学的过程中都应体现综合的核心素养的培养.数学的核心素养中可以划分为数学抽象、逻辑推理、数学建模、数学运算、直观想象和数据分析.数学教学中着重培养的核心素养不仅仅是数学能力上的提升,也不仅仅局限于数学教材中的具体知识和技能.数学教学中发挥学生的主体性其实就是让学生在学习数学知识和技能的基础之上,对于数学的思想系统和习惯有一定的认知,只有和数学教学的目的直接联系起来,才能让学生真正理解、掌握转化与化归思想方法,最终达到灵活运用其解决实际数学问题的目的.
2.2 化归与转化方法的实际应用
例如在三元一次方程组的教学中.教材中明确给出了三元一次方程组的相关概念.且在上一个章节中,学生已经学习过了二元一次方程组的相关概念及应用题解答.在解题过程中,已经初步形成了对这种方程组的解题思路.因此在本次的三元一次方程组教学中,教师就可以运用化归与转化的思想方法,按照教材内容引导学生了解三元一次方程组的概念,并让学生尝试思考本堂学习内容同之前二元一次方程组的联系,使用“代入”、“加减”的思路,尝试将三元一次方程组转化成二元一次方程组.学生熟练掌握转化的方法后,教师可将这一思路总结为“消元”,通过几道题目的训练,提升学生对“消元”转化的熟练度.
在这一节的教学任务中,能够体现的情感、态度和价值观是让学生在遇到陌生的知识时,能够学会调动既往学到的熟悉的知识内容,并尝试将陌生的知识转化为熟悉的知识,将难以解答的问题转化为便于解答的问题,在学习过程中充分感受到化归与转化的数学学习方法带来的解题便利.
为了进一步提升在三元一次方程组学习中,学生对化归与转化思想的思考和理解能力.教师可以创设与学生现实生活贴近的问题情境.
例如 让学生以一场兵乓球比赛为例.已知的是一支队伍在比赛的10局中一共得分18分,比赛的规则是赢一局会加三分,输一局不得分,平局则会得一分.这支队伍的10局比赛中,胜场次数等于平场和负场次数之和.问题时这支队伍赢、输、平局的次数.教师引导学生将赢、输、平局的次数,分别设为x、y、z三个未知数,并列出{z+y+z=10、3x+y=18、x=y+z的方程组.联系之前学过的二元一次方程组,需要运用“消元”的思路将三元转化为二元,也就是要消除掉一个未知数,即可运用之前学过的知识解答出问题.可以将x=y+z,带入到公式{z+y+z=10、3x+y=18中,就得到了{2y+2z=10、4y+3z=18,得出{y=3、z=2.将{y=3、z=2,带入到方程x=y+z中,得到x=5.
这样的代入法解三元一次方程,通过化归与转化的思想提升了解题效率.引导学生联系二元一次方程组的解法,一方面帮助巩固了旧知识,另一方面有助于在联想中激发学生对数学学科的兴趣,对数学学科的教学效果产生积极作用.
化归与转化思想方法,在平面几何的教学中同样可以应用.
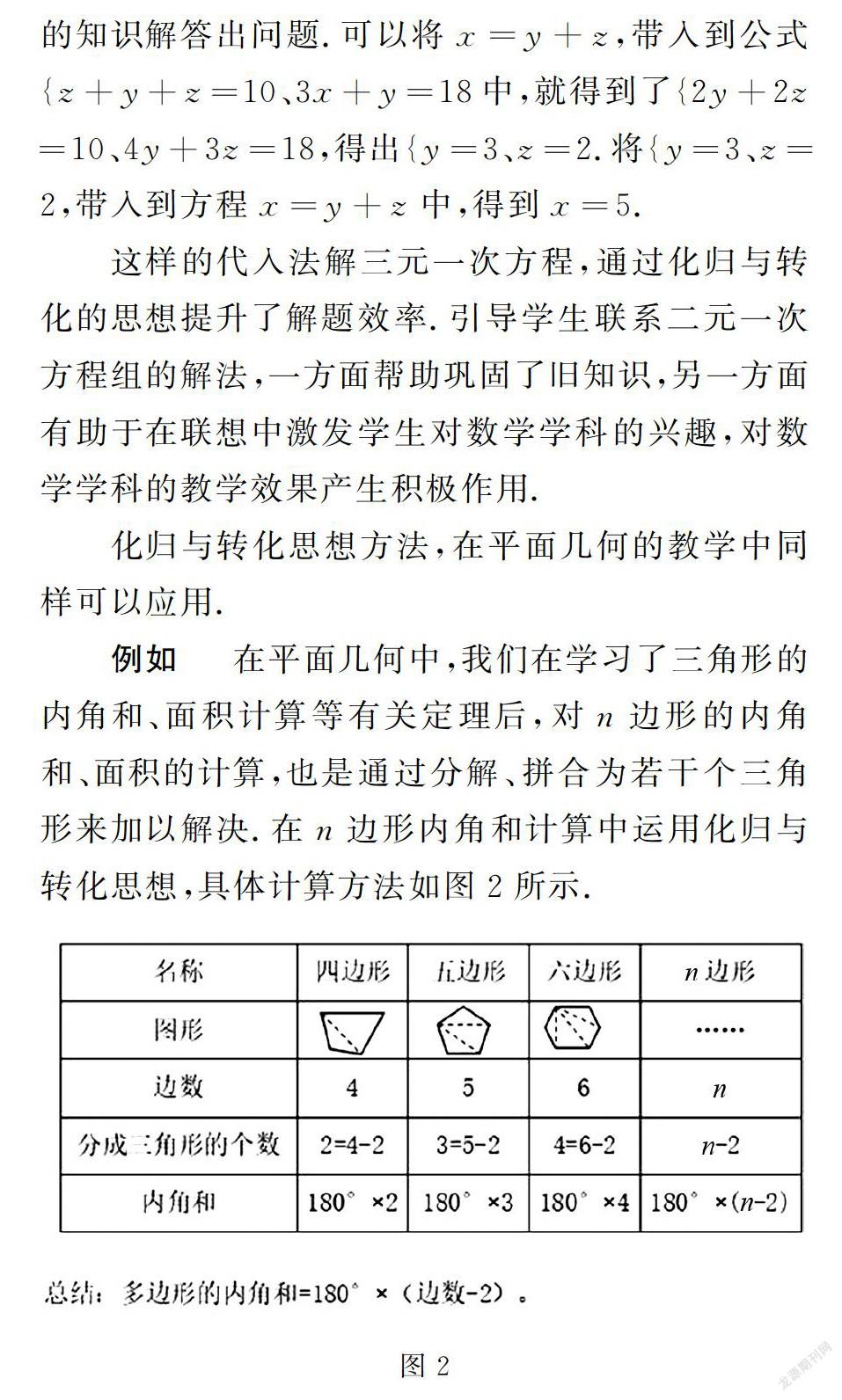
例如 在平面几何中,我们在学习了三角形的内角和、面积计算等有关定理后,对n边形的内角和、面积的计算,也是通过分解、拼合为若干个三角形来加以解决.在n边形内角和计算中运用化归与转化思想,具体计算方法如图2所示.
总结:多边形的内角和=180°×(边数-2)。
3 结语
结合以上的分析内容,可见在初中数学教学中运用化归与转化思想,有助于提升教学效率和效果,让学生转变机械式学习方式,在数学学习中不断锻炼思维能力,帮助提升数学学科成绩.因此,教育工作者未来应对数学教学中化归与转化思想的应用原则是加深学生的学习和理解,以提升教学能力和教学工作质量.
参考文献:
[1]陈土树.求解简单多面體外接球问题的策略 ——兼谈数学抽象之化归与转化思想[J].文理导航(中旬),2018(5):28-29.
[2]彭伟.运用化归与转化学习策略培养学生数学核心素养[J].科学咨询,2021(16):204-205.
[3]张传鹏.基于学生思维能力提升的数学化归与转化——以一类向量三点共线问题为例[J].上海中学数学,2021(7):42-44.
[4]宋予林,刘鑫钧.莫愁前路无“解法”转化化归“本领”大——对高三解题教学中数学素养渗透的反思[J].数学教学通讯,2021(6):66-69.
[5]孙艳伟.化归与转化的数学思想在初中数学课堂中的应用[J].新教育时代电子杂志(教师版),2021(42):49-50.
[6]牛松涛.浅谈转化与划归思想解决简单数学问题[J].海外文摘,2021(9):108-109.
[7]王翰文.基于“转化与化归”思想的高中数学解题研究[J].华夏教师,2018(23):71-72.
[8]刘立晓.巧用转化与化归提高学生数学能力[J].新课程·下旬,2018(6):13.

