长方体表面积计算不止“表面”那么简单

江苏扬州市江都区郭村镇塘头小学（225238）张应贵

“长方体表面积计算”的教学重点是让学生熟练掌握长方体表面积的计算方法和公式，并会根据不同问题的特性灵活运用这些公式去解题。本课的教学难点为脱离具体图形，单纯根据长方体的长、宽、高来推算其上、下、左、右、前、后六个面的面积，以及判断任意两条棱相乘得出的是哪个面的面积。

一、唤醒旧知，导入新课

大量的教学实践表明，“温故而知新”对学生的数学学习而言是非常有价值的经验，也是促进数学学习构建的力量来源。因此，在“长方体表面积计算”教学中，教师需要围绕长方体表面的构成情况，以及各个面的形状、面积计算等创设学习情境，引导学生在复习中巩固已有的知识经验，为学习长方体表面的构成、表面积的计算提供坚实的保障。

【教学片段1】

师（出示一个长10厘米、宽3厘米的长方形）：这里有一个长方形，你能迅速算出它的面积吗？

生1：10×3=30（平方厘米）。

师（用课件演示6个小长方形拼成一个大长方体）：此时此刻，映入你们眼帘的是哪种形状？

生2：长方体。

生3：它是由6个小长方形围起来的大长方体，从前面的学习中，我知道它相对的面是一样的。

师：没错，这就是长方体。对于长方体，大家已经有所了解，那么具体是哪些知识，请大家说一说。

生4：长方体有上、下、左、右、前、后6个面，8个顶点，12条棱。长方体相对的两个面完全相同。

师：现在我们接着研究长方体的有关知识。

【评析】

利用长方形引出长方体，看似平平无奇，实则匠心独运，不但可以瞬间激活学生对旧知识的回忆与经验，而且通过回顾长方形的面积计算方法，为后面学习长方体表面积的计算埋下伏笔，消除了长方体表面积这一概念给学生带来的陌生感，让学生隐隐感到长方体表面积和长方形面积之间有着千丝万缕的关系，既然长方形面积计算这么简单，那么长方体表面积计算也不会难。学生畏难情绪一扫而光，学习信心大增，对未知内容充满期待。教师用课件动态演示了从平面到立体的升级跃迁过程，让学生直观地看到三维立体图形也是由平面图形拼组得到的。学生在这一过程中建立了空间观念。学生通过对长方体的概念和基本特征的概述，为后续学习打下坚实的基础。

二、初步感知，自主探索

要让学生学习和研究长方体表面积的计算方法，首先要帮助学生感知长方形表面积的存在，认识长方体表面积的概念，其次要引导学生通过自主学习与同伴互助等学习活动，更清晰地认识长方体表面的构成，并在相应的思考分析后，初步感悟长方形表面积的基本要义。因此，在此阶段教学中，教师要围绕促进学生感知长方体的表面、感悟长方体表面的构成等方面思考、谋划，力争让学生通过观察、比较和讨论，对长方体的表面积进行建构，使得学生的学习效果有所提升。

【教学片段2】

（教师板书：长方体的表面积）

师：看到这个标题，大家有何感想？

生1：长方体的表面是不是就是指刚才那6个长方形呢？

生2：到底什么是长方体的表面积？它与长方形的面积有什么联系和区别？为什么要加一个“表”字？

生3：长方体的表面积该怎么计算？

……

师：你们提出的这些问题都值得引起高度重视，每个人都得打起精神来研究。下面咱们就来一探究竟。要想准确把握长方体表面积的定义，不妨先从实物的表面入手，寻找突破口。你们就地取材，随手找一个物品，摸一摸其暴露在外的面，教室内的书桌、黑板、文具盒、书包、橡皮、门窗等都可以用作学具。

（学生观察、触摸物品表面）

师：我看到不少同学抚摸课桌桌面，你摸到的算是课桌的表面吗？

（有的学生沉默片刻后摇头否认，有的学生蹲下身去摸桌腿和桌底以及桌子背面）

师：看来任何一个物体都有表面，而且不止一个表面，那长方体的表面究竟是怎样定义的呢？

生4：长方体暴露在外的所有平面就是它的表面。

师：那么长方体一共有几个面呢？

生5：6个。

师：长方体6个面的面积总和就是长方体的表面积。

（教师板书：6个面的面积总和就是长方体的表面积）

【评析】

肉眼观察只能看到二维平面有限的空间，难以形成透视效果，需要不停转动观察对象，进行想象才能勾勒出三维轮廓，但是通过触摸就可以弥补肉眼观察的不足。学生通过触觉信息较为准确地感受观察对象的各项特性，如物体表面的数量、大小、形状、相对位置关系等。还有就是通过触摸能感知平面是否暴露在外面，有的物品的某些面就藏在物体里，那是内面，不算表面，如双层玻璃保温杯的内胆就是内面。学生通过用眼看、动手触摸，对“表面”有了准确认知。在摸课桌面时，学生明确了生活中的表面与数学中的表面有所不同，课桌的表面不仅是桌面那一块，还包括桌腿在内的所有暴露在外的面。学生意识到任何物体都有表面，才能更深入地理解表面积存在的意义。

三、尝试探索，感悟规律

引导学生探寻各种疑问的真相，使他们投入学习研究，是构建有效学习、打造智慧课堂的重要举措，也是进一步彰显“以学为中心”的教学理念。因此，在这一阶段的“长方体表面积计算”教学中，教师就得营造氛围，鼓励学生进行分析、自主探索，让他们顺利走向自主探究长方体表面积的计算方法的智慧之路。当然，在这里，教师既要履行好引导职能，及时对学生进行指导，又要用核心问题串连教学环节，使得学生的学习活力尽情释放，使学习实效不断提升。

【教学片段3】

师：瞧！老师手中托着一个长方体“月光宝盒”。“月光宝盒”6个面的面积总和就是它的表面积。你能描述一下你手中“月光宝盒”的复制品的表面积是指什么吗？

（学生触摸“月光宝盒”表面）

师：现在，老师手中托着两个长方体“月光宝盒”，但不知哪个的表面积更大。

生1：左手中的宝盒的长更长，宽也更宽，高也更高，不难得知它的表面积大于右手中的宝盒的表面积。

师：判断一个长方体表面积的大小，就是看它的长、宽、高。不可否认，长方体表面积的大小确实与它的长、宽、高息息相关。请你动手测量一下你面前的长方体的长、宽、高，然后计算它的表面积。

活动：

（1）小组合作测量不同的长方体的长、宽、高；

（2）学生独自计算长方体的表面积。

师：大家量好了吗？展示交流一下。汇报前，先提供你测量的各项原始数据。

学生汇报（如表1）。

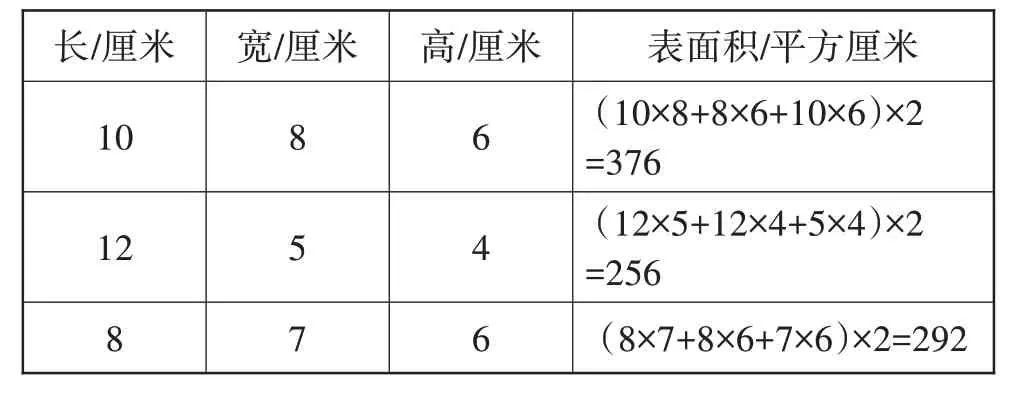
表1 各长方体的长、宽、高及其表面积

师：你写的算式中10×8是求哪个面的面积？

生2：长方体的上面。这个面的面积是用长方体的长乘宽来求的。

师：8×6是求哪个面的面积？

生3：右面。这个面的面积是用长方体的宽乘高来求的。

师：10×6是求哪个面的面积？

生4：前面。这个面的面积是用长方体的长乘高来求的。

……

师：很好，大家都顺利求出了长方体的表面积，值得表扬。虽然长方体大小不一，但它们表面积的计算方法都是一样的，都是通过对长、宽、高三项数据的两两相乘，再将它们的乘积相加算出的。也就是把长、宽、高两两相乘，先求出3个相邻面的面积，再乘2，求出6个面的面积总和，这就是长方体的表面积。

【评析】

引导学生探究长方体表面积大小与其长、宽、高的联系。学生通过测量、计算等自主探究途径，将长方体的表面积分解到每个长方形的面积。在此基础上完成第一次归纳总结，即把长、宽、高两两相乘，先分别算出3个相邻面的面积，再根据相对面面积相等，将三面之和一齐扩大2倍，求出6个面的面积总和，也就是长方体的表面积，一次性利用对面的相等性和邻面的差异性简化公式，避免了一个面一个面计算的烦琐过程。

四、概括提升，总结方法

众所周知，有效的学习是需要去提炼的，需要去构建相应的数学认知体系，更需要在一定的磨砺中建立起对应的数学思维模型。小学生对长方体表面积计算的学习也需要经历一个积累、深化、完善、建构的过程。因此，在“长方体表面积计算”教学的最后一个环节中，教师还得围绕教学目标，设计一系列梳理回望、概括归纳、抽象总结等学思活动，助力学生把所学的内容进行必要的反刍，提炼出精华，积累较为理性的学习经验，建立起数学思维模型，使得他们的数学学习更加智慧，充满无尽的活力。

【教学片段4】

师：你们刚才都总结了长方体表面积的计算方法，如果隐藏具体数据，只用长方体的长、宽、高来抽象表示，你能写出长方体的表面积公式吗？

［学生交流后，得出结论：长方体的表面积=（长×高+长×宽+宽×高）×2］

师：“长×高”求的是哪个面的面积？

生1：前面和后面。

师：“长×宽”呢？

生2：上面和下面。

师：“宽×高”呢？

生3：左面和右面。

［教师出示课件：长×高=前面（后面）的面积；宽×高=左面（右面）的面积；长×宽=上面（下面）的面积］

师：若要计算某一个面的面积，只要将这个面相邻的两条棱相乘就行。

【评析】

学生在自主总结长方体表面积公式时，详细分析计算原理，然后根据这个原理反思，并进行二次观察，发现一些难以觉察的细节，即若要求某个面的面积，就用这个侧面相邻的两条棱相乘即可。这个细节的发现需要学生对长方体的直观图极其熟悉，而且随时可以想象出来。其中，存在一定的对应规律就是长和宽围成的是上、下面，长和高围成的是前、后面，宽和高围成的是左、右面，发现这些规律的前提是对长方体棱的分布与位置关系的熟练掌握。

长方体表面积的概念解读与学习其实并不难，教师应看到长方体表面积概念的背后蕴含的表面积计算算理，丰富表面积的计算形式，优化表面积的计算方法，内化表面积的计算算理，从而让长方体表面积计算变得简单。