基于前测分析 让练习更有效
——“写三位数乘二位数的积的最大算式”练习题的教学实践与思考
浙江建德市实验小学(311600)鲁孟军
一、问题起因
人教版教材2011年版的四年级上册第51页有一道练习题:用0,1,2,3,4,5组成三位数乘两位数的乘法算式,你能写出几个?你能写出乘积最大的算式吗?根据教学经验,学生解题的错误率非常高。虽然学生在三年级时接触过简单的排列组合,知道具体形象的事件可以通过列举得出结论,但解这一题要将5个数字进行排列,并且组成具体数时还要考虑0的位置,这已经超过了他们的认知水平,因为要有序且不遗漏地把这些组合写完,得花一定的时间,确实不容易。此外,用这五个数字组成的三位数乘二位数的算式很多,许多算式相似度非常高,学生很容易混淆,也不能通过口算轻松得到正确答案,想要准确找到积最大的算式,这对他们来说确实有较大难度。
计算练习是最枯燥的,在考试中又是学生失误最多的部分。教材编排的目的是希望学生能在寻找乘积最大算式的规律方法的过程中进行不断的计算练习,以夯实计算基础。
因此,教学时可以结合这道题的分析过程,通过任务驱动,让学生从被动计算练习转为有目的地主动计算,在不断验证、探索规律和方法的过程中自然地进行计算练习,提升学生的数感。同时,引导学生学会理性思考并用正确的方法进行推算,提升学生的推理能力和解决问题能力。
二、前测分析
1.设计前测练习
因为解题需要三位数乘二位数的相关知识,所以就以学校四年级2个班的学生(共80人)为测试对象,设计两道前测题:
前测题1:用1,2,3,4,5这五个数组成三位数乘二位数的乘积算式,你可以写出多少个算式?
前测题2:用1,2,3,4,5这五个数组成的三位数乘二位数的算式中,乘积最大的是哪个算式?
前测题与教材题目有所不同,把原题中的“0”去掉了,这主要是因为在进行竖式计算时,末尾的“0”是不用参与计算的,所以用0就不能有效暴露学生的思考过程,去掉后,更能反映学生的思考过程,展示学生解决这类题所用的方法。
2.分析前测结果
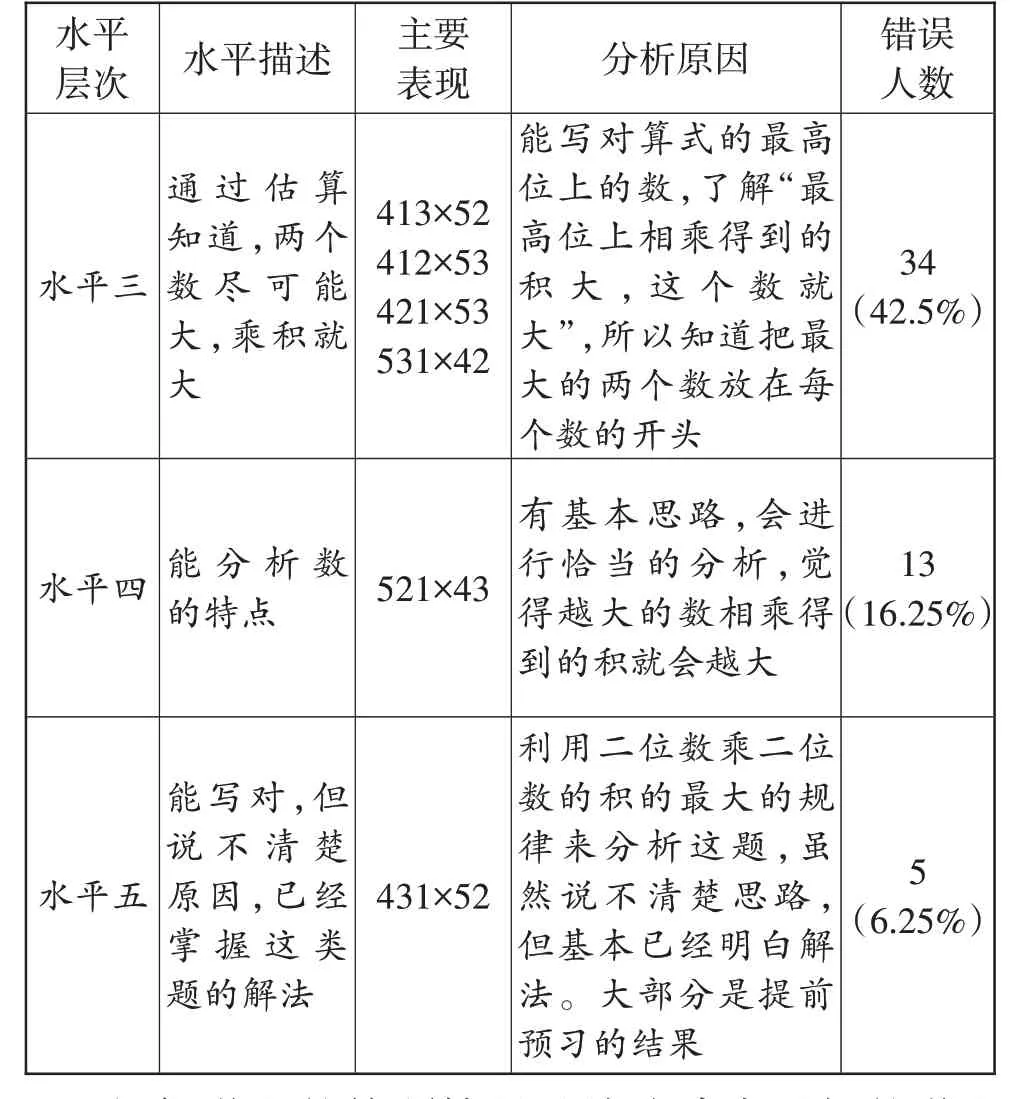
依据前测题2的答题情况,给学生划分了几个不同能力层次:

表1
续表
根据学生的答题情况及从访谈中了解的学生思考过程得知,水平一到水平三的学生占了大多数,这说明学生整体上对这类题目的认识是模糊的;由于学生水平能力的不同,学生解题出现的错误也明显不同,最主要还是欠缺逻辑推理和估算的意识,同时计算能力也有所不足。
因此,教师应该注重数学模型的建构,重视估算的应用,强调计算能力的训练,借助多种途径引导学生找到正确的解题方法,提高学生的分析问题能力和逻辑推理能力。
三、实践反思
1.组合算式,引发思考
这节课主要是通过复习三位数乘二位数的计算,提升学生的逻辑推理能力。对于前测题1,由于留给学生一定的时间,部分学生能根据数的排列和组合写出较多的算式。对于前测题2,学生基本都是写错的,水平一到水平三的学生占了大多数。因此教学时宜从教材的习题切入,以降低难度。
【教学片段1】
师:请用0,2,3,4,5这五个数组成三位数乘二位数的算式。能写几个就写几个。
生:根据数的搭配组合,我先写2开头的,比如……
师:是的,根据数的组成可以写出72个算式(如图1)。这些算式都是三位数乘二位数的算式,也就是我们刚刚学习的算式。那怎样进行三位数乘二位数的计算,需要注意什么?

图1
72道算式的展示,让水平一的学生明白这些算式的组合方式,了解算式的特点。由于搭配算式不是这节课的教学目标,这72道算式的展示是根据估算结果来排列的,目的是为后面的教学做铺垫。
2.引用估算,确定方向
在解决数学问题时,需要学生具备估算意识,能有目的地分析数据,思考算式。
【教学片段2】
师:在这么多算式中如何找出结果最大的算式?
生1:计算出它们的结果。
师:那可要花些时间了。先想一想,哪些算式的乘积一定不会是最大的?为什么?(引导学生估算)
生2:我发现,通过估算,第一列算式的结果都是6000多,第二列算式的结果都是8000多,第三列算式的结果都是10000多,第四列算式的结果都是12000多,第五列算式的结果都是15000多,第六列算式的结果都是20000多,所以一至五列算式的结果都不可能是最大的。
师:那你有什么发现?
生3:只有把最大的两个数分别放在两个因数的首位,才可能使得到的乘积最大。
实践中让学生对课件展示的72道三位数乘二位数的算式进行估算,把乘积一定不会最大的算式给找出来。这一问题的提出,让水平一和水平二的学生很快就有了思考的方向,这样学生很快就否定了一至五列的算式,明白了解决这类题的一个基本特征:两个因数的最高数位上的数应该是最大的两个数。这样一来就有效提高了水平一和水平二的学生的解题水平,让学生感受估算的重要性。
3.计算训练,明确方法
因为这节课是计算练习课,要让学生多加练习,进而在计算练习的基础上明确解题的方法,所以让学生先计算课件展示的12道算式(如图2)。这些算式的计算结果差距小,更能体现精确计算的重要性。
【教学片段3】
师:通过前面的分析,积最大的只可能出现在第六列的算式中,下面请计算这列的12个算式(如图2)。(部分学生上黑板板演)
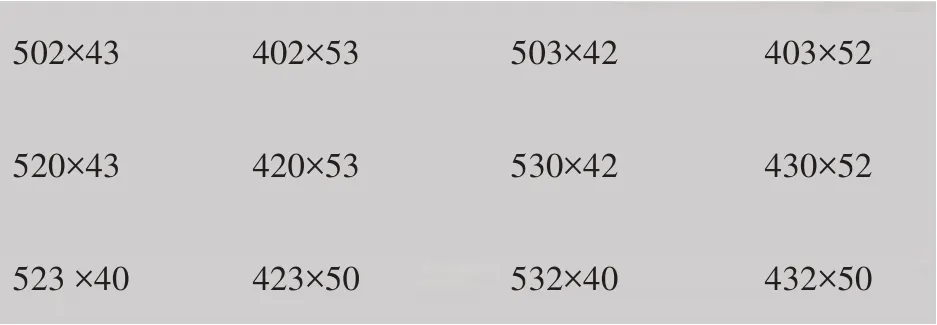
图2
师:有了算式结果后,如果在确定两个因数的最高位后,再选两个数字,你会选哪两个数呢?
生1:选余下数中最大的两个数字,这样得到的结果会比较大。
师:是的,我们来看看这些算式(如图3)有什么特点。

图3
生2:先将5,4分别写在两个因数的最高位,再将3,2分别写在这两个因数的第二位,0放最后,这样的乘积结果比较大。
因为有前面环节的铺垫,学生能根据计算结果找到四个最接近的算式,并很快得到解题方法。通过这样的思考,学生明确了写乘积最大算式时选择数字的顺序:最大的两个数分别放在两个因数的最高位,再从余下数中选择最大的两个数,分别放在两个因数的第二位,这样依次进行。由计算验证得出方法的过程,使学生的思维在解决这类问题时变得有序,有效解决了水平三学生的问题。
4.计算模型,整合方法
数学思维的火花是在不断的思维碰撞中产生的。对得到的四个算式的结果进行比较后,学生会将它们分成两组,因为0在末尾不参与计算,教师就可以继续引导学生进行推理。
【教学片段4】
师:现在我们知道430×52和520×43的计算结果最大,这是为什么?
生(齐):不知道。
师(出示三年级“积变化规律”的内容,如图4):两个数的和不变,它们的差越小,乘积越大。

图4
师:现在你知道原因了吗?
生1:比较43×52和42×53,可以发现差分别是9和11,因为差越小,积越大,所以43×52的乘积比较大。
师:你能举个例子来证明吗?
生1:56×47比大57×46,58×63比大53×68。
师:请大家通过计算验证。
师:现在学的知识是以三年级知识为基础的,所以大家一定要学好每一个知识点。
学生通过复习知道,在三年级的“长方形面积”就学过“当长和宽越接近时,面积越大”(如图4),后来接触过一些和相等的两数相乘的算式,也知道“它们的差越小,积越大”。通过引导,学生慢慢会发现,将三位数的个位0去掉后就是两数相乘的计算模型,52与43更接近,它们相乘的积会更大。让学生明白写乘积最大的算式的方法是早已学过的,了解这题的本质是什么,这是学生掌握解决这类题的方法的一个关键。
5.改变数字,应用模型
至此,学生已经掌握了解决这类题的数学模型,也进行了多组计算练习。这时,教师可将数字0变为与前测题一样的数字1,让学生进行分析、计算、验证,在巩固解题方法的基础上再次进行计算练习。
【教学片段5】
师:如果我将0改为1,现在5个数组合的三位数乘二位数的算式中,乘积最大的应该是哪个算式?请想一想,写一写。
生1:521×43,431×52。
师:请通过计算说明它们哪个的积更大。想一想,这个乘积最大的算式排列的方法是怎样得出的?
生2:通过计算知道431×52的积更大,因为放在43后面的1去乘52积会比放在52后面的1去乘43更大。
生3:通过计算知道431×52的积更大。431-52的差更小一些,所以积会更大。
通过观察和计算,学生明白:先选择最大的5和4,接着选2和3两个数,应用“两数差越小,积越大”的方法组成二位数乘二位数的算式,再把1放在小的二位数后面,这样组成的三位数与二位数的差更小,积也会更大。当然也可以用与1相乘的积的大小来确定1的位置,最后得到结论:先选最大的两个数,再选余下最大的两个数,应用两数差越小积越大的方法,把第三大的数放在第二大的数后面,第四大的数放在第一大的数后面,最后一个数放在小的二位数后面,这样组成的三位数与两位数的差更小,积也会更大。对于这个解题方法,让学生明白思考的顺序是关键,不需要过于强调方法叙述的完整性。
6.字母模型,巧妙解法
由于学习能力的差异、理解能力的不同,总有一些学生无法掌握解题方法。此时,教师可以根据模型的特点,结合字母模型,把各数的排列巧妙地与笔画顺序结合起来,让学生感受学习数学的乐趣。
【教学片段6】
师:请写一写2,4,6,8,9和1,3,5,7,9这两组数分别组合成三位数乘二位数乘积最大的算式。
师:刚才我看到还有不少同学写不出来。下面介绍字母解法,它能帮助大家更轻松地写出算式。
师(展示“U”字解法,如图5):按字母写字顺序,结合前面学习的解题方法,先写最大的两个数,再写余下最大的两个数,最后一个数最后写。

图5
师:说一说这字母法和前面的学方法有什么共同之处。
借助字母模型,直观地将选择数据的顺序呈现出来,让学生有位置模型可以借助,学生理解起来就容易多了。课后访谈发现,学生基本愿意用这种数形结合的方法来解题,不太愿意用前面说理的方法。
纵观整个教学实践过程,学生经历了多次的认知冲突与碰撞,经历了问题分析、计算练习、验证反思等过程,借助不断地推理,在解决写乘积最大的算式过程中进行了有效的计算练习,建立了解决问题与计算应用之间的联系。通过不断地计算和验证,学生学会推理和研究。
教材中还有很多类似的习题,如何去教学这些学生感到熟悉但又不太容易解决的问题,需要教师思考。值得注意的是,课堂教学必须以尊重学生已有经验为基础(起点),重视教材解读与重构(题组),重视拓展材料的设计(变式),重视启发学生(方法),通过对有层次和有结构的题组进行思考、尝试、实践、探究等活动,利用学生已有的知识水平和经验,提高学生解决问题的能力,让学生在更高的层级感悟数学内在的价值,使学生的练习更有效。

