在磨课中探索计算教学的有效手段

江苏海安市曲塘镇双楼小学（226661）李彦霏

纵览整个小学阶段的计算教学内容，“除数是小数的除法”是一大难点，教师难以将其中的奥妙讲清楚，学生也难以掌握其算法精髓，对其中的换算规律一知半解。这类计算是计算教学中的典型问题，能够反映教师的计算教学水平，也能反映教师对教材的处理能力。学生能熟练、正确地计算除数是整数的小数除法（以下简称“整数除数除法”）是教学除数是小数的除法（以下简称“小数除数除法”）的基础。小数除数除法的基本计算原理就是运用商不变规律，将小数除数转化为整数除数，然后根据整数除数除法的计算法则和运算性质算出商。教学时，教师要帮助学生形成将未知问题转化为已知问题的数学思想，并积累这种学习新知的宝贵经验。为达成教学目标，笔者进行了同课异构处理，现展示部分重要教学片段，与大家共同探讨计算教学的有效策略。

一、导入不同，效果不同

首次执教时，笔者采用题目导入法，出示了两个问题。

1.先直接划掉下面各数的小数点，将其变为整数，再看看每个新数比原数扩大了几倍。（口答）

3.7 2.54 6.248 21.67

2.填表，发现并归纳被除数、除数和商的变化规律。

24 12被除数除数商240 120 1200 2

总结：在除法算式里，被除数和除数做同步变化，商不变。

此环节用时约5分钟，目的是让学生初步意识到本课的教学内容与商的变化规律有关。这样，学生学习时就会对初步发现的规律格外注意，积极思考，为后面的深入探究做好铺垫。遗憾的是，这个环节的设计似乎低估了学生的能力，且与新授课程有些脱节，没能将学生的已有经验彻底激活，也没有成功引发学生在关键点上的认知冲突。

因此，在重构教学方法时，笔者痛定思痛，决心整改，锁定学生的真实知识起点——整数除数除法。

笔者出示口算题：

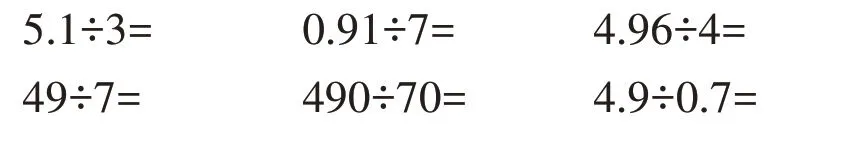
首先，第一行的三道题是通过复习的方式将学生的真实学习起点暴露出来，作为学习小数除数除法的有力跳板。第二行的三道题则是通过对比，诱导学生发现商不变规律，为顺利实施转化埋下伏笔。其中，最后一题的除数由整数变为小数，但思路仍是承接前几题，如此，学生仍能凭借直觉和经验作答。当然，这道题也只是一个诱饵，学生能够根据计算第四、第五题发现的商不变规律正确作答，说明他们的已有经验被精准激活，刚好为这节课的新知学习做好了思想准备。整个教学环节“短小精悍”。计算教学的导入应该干脆利落，一针见血地激活学生的已有经验。此外，还要加大口算训练力度，若能在口算中做到复习引入，就能事半功倍。

计算教学的关键是渗透算理，而算理有原始算理和最近算理之分，小数除法运算的算理就是运用商不变规律，将小数除法转化为整数除法。这种算理是原始算理，笔者第一次教学时以这一算理为铺垫，引出小数除法，这种做法忽略了原始算理和现实算式间跳跃性非常大的事实，步子迈得太大，导致前后脱节，虽然逻辑上有关联，但是这种关联周期长，容易被忽略，从整数除法到小数除法，中间需要整数除数除法来过渡和缓冲，这个过渡期和缓冲期的算理才是教学的最近发展区，也就是最近算理。小数除数除法，就是以将除数转化为整数为目标，根据商不变规律，将被除数和除数同时扩大相同的倍数。也就是说，其最近算理是第一算理，商不变规律是第二算理，原始算理处于最末的位置。

二、修改细节，突出主体

对于学生的自主探究，笔者首次执教时是这样设计的：

1.出示题干：武商量贩店里的胡萝卜售价是4元/千克，李阿姨在武商量贩店买胡萝卜花了7.84元；中百仓储里的胡萝卜售价是4.2元/千克，王叔叔在中百仓储买胡萝卜花了7.98元。

（1）让学生仔细阅读各项条件，然后回答问题：比一比，谁买的胡萝卜多？

（2）让学生列出算式并尝试解答。

2.请三位学生上台板演，指名两位学生演算算式“7.98÷4.2”，然后请他们自述遇到的困难。（揭示：转化）

3.教师示范正确解题过程，并作详细说明。

4.用课件再次展示解题过程，并粗略总结：首先要判定除数的小数位数，然后将小数点右移至末位数字后，使小数变为整数，被除数的小数点也向右移动相同的位数。

以上的执教方式有两个不妥之处：一是贸然让学生上台演算，很唐突，且部分学生在计算“7.84÷4”时耗费了较长时间，导致后面小数除数除法这个重点不突出；二是请学生上台尝试演算“7.98÷4.2”时，台下的学生就干脆瞪眼旁观，没有积极参与思考。总的来说，学生的参与度低，独立思考与尝试流于形式，内涵不足。

鉴于此，笔者在重构时对教法和情境都进行了大刀阔斧的改进。

直接呈现情境：中百仓储里的胡萝卜售价是4.2元/千克，王叔叔在中百仓储买胡萝卜花了7.98元。

师：仔细阅读以上条件，自编数学问题并列式。

生1：王叔叔买了多少千克胡萝卜？列式为7.98÷4.2。

师：这道算式和我们前面学过的算式不大一样，你看出来了吗？

生2：这道算式的除数是小数，而之前学的算式除数都是整数。

师：有同学能大致估算出算式的结果吗？

生3：在2千克到3千克之间。

生4：大概是二点几千克。

师：设法将新型算式“7.98÷4.2”转化为旧知，和同桌研讨，并写下你的思路和设想。

（教师巡视，然后请学生把自己的计算方案写到展示板上，选取两份典型作业投影展示，如图1）

图1

这两种方法中，第一种方法是利用商不变规律转化算式，然后用“79.8÷42”的商作为原算式的商，第二种方法则是在竖式中直接转化。还有部分学生将7.98元和4.2元化成79.8角和42角来计算，这是紧紧依靠现实意义来换算。在总结反馈环节中，大家指出这种化元为角的方法其实与第一种方法别无二致。最后，教师用课件动态演示小数点位移的情况。

以上课程设计的重构，首先，对例题的改编，直接呈现新授内容，顺便调用了学生的估算技能，让学生在探究新算法时目标更加明确。其次，参与面辐射全体，每位学生都能独立重塑自己的认知形态，将少数学生公开板演改为全部学生在展示板上尝试，每个人都能在独立思考后发表见解。最后，让学生上台展示汇报，自述思路，学生的思路得以充分展现。交流中，其他学生可以自由质疑、补充、修正他人的想法，相互促进理解算理，然后一起总结算法——要把小数除数转化为整数除数。在日常教学中，教师惯用新旧知识对比这一手段，但一定要把握好时间，尽量在最短时间内引出新知。就本节课而言，花在整数除数除法上的时间不宜过多，如果要对比新旧知识，其实开场的口算就已经做到。

知识是循序渐进发展的，高深的知识一般都是从低处一步步往上攀登获取的，这个缓慢爬坡的过程不能省，没有前后联系过渡，新知就如无源之水、无本之木。不过，爬坡也有不同的爬法，是爬陡坡还是爬缓坡，是直着爬坡还是迂回着爬，是有讲究的。第一次教学中，笔者有意将整数除数除法用来做铺垫、搭梯子，但是4元/千克和4.2元/千克没有直接关系，“7.84÷4”和“7.98÷4.2”仅仅是存在高度差的两个孤立的算式，没有形成坡度对接，学生做完“7.84÷4”之后，没有获得对解决“7.98÷4.2”有益的启示和方法，无非是爬完一座矮坡再爬另一座高坡。而改进后的教学，只保留一个算式“7.98÷4.2”。学生在计算受阻后自然而然想到估算法，这是个尝试爬坡的过程，但是坡度太大，于是笔者启发学生将其转化为像“79.8÷42”这样的整数除数除法，这就是教学生搭梯子，建立螺旋状的省力坡面。学生通过“搭梯子”，便想到利用商不变规律来同时调整被除数和除数。

三、适当调整，磨炼技能

在练习环节中，笔者首次教学是照本宣科。

1.填数。（口答）

0.34÷0.2=（）÷2 7.82÷0.34=（）÷34

0.34÷0.02=（）÷2 0.782÷0.034=（）÷34

2.口算。

3.9÷3= 0.81÷9= 0.35÷7=

3.9÷0.3= 0.81÷0.9= 0.35÷0.07=

3.先判断下列各题中的数需要怎样移动小数点，再计算。（先口述，再计算）

以上练习中，第1题的重点在于如何调用旧知，而后再口算。口算虽然只是热身练习，但却是一个必备技能，最后才是笔算练习。环节的设计看起来没什么问题，但其实把顺序调整一下更好。如把第3题的笔算练习调整为第1题，第1题填数的专项训练推后作为第2题，第2题的口算放在最后。

第二次教学时，笔者按上文所述进行调整，同时对原来第3题的最后一个式子进行“手术”，换成“3.7）3.848”，目的是让学生不仅学会处理除数是两位小数的情况，还学会在试商时处理中间商“0”的情况。同时，将原来的第1、第2题设为必做题，第3题设为选做题。如此改进后，笔者发现学生接触新知后马上能通过笔算练手，及时检验算理，十分有助于技能的掌握。经过适量的笔算练习后，再进行“小数点同步位移”的专项训练，深入揭示算理，最后安排口算。此时，由于学生对算理理解透彻，又有笔算经历打底，口算技能的形成就水到渠成了。

回顾、梳理本节课的教学，在两次试教中，笔者均安排了改错、估算、应用与小结等环节，通过持续努力，转化思想已经深入学生心中，效果良好。

学生会学了后面忘了前面，教师也会教了后面忘了前面，虽说教学有进度、有重点，到了哪座山就唱哪支歌，但是学了后面只顾后面，将前面忘得一干二净，就会形成知识的断层，不利于学生的长远发展。比如，若学生学习小数除数除法，只顾着怎么将算式转化成整数除数除法，注意力全部集中在转化上，对整数除数除法的计算方法就反而生疏了。若想学生在学会转化的同时巩固新知，顺便回顾旧知，最好的办法就是出题时，将小数除数除法中涉及的整数除数除法的所有可能特殊情况都编排一遍，再现当初的真实情况，如商中间有0的情况，商的末尾直接添0的情况，还有商的前几位直接补0的情况，将这些特殊情况都补充进来，这样学生的除法认知结构才算完善。

经过以上的磨课、重构过程，笔者深有感触：首先，计算教学离不开估算奠基，要留足空间，让学生在交流展示中厘清算理，形成科学的算法模式，逐渐形成计算技能；其次，口算与笔算能力的培养要同步进行，口算可以促进笔算能力的加强；再次，计算教学要注重“算用结合”，学以致用才能体现计算的价值，彰显数学真谛；最后，在计算教学中，要注意培养学生的反思意识，让学生在反思中不断进步提高，完成自我提升。