让“线段图”活起来
——以“和倍问题”教学为例
浙江绍兴市柯桥区管宁实验小学(312030)魏 雯
线段图是由几条线段组合在一起,常用来表示问题中的数量关系,是用于题意分析和问题解答的一种平面图形。利用线段图可以帮助学生解决一些稍复杂的问题。尤其到了小学的中高年级段,很多学生对于一些抽象的问题理解起来相对比较吃力,而线段图的准确表达能帮助学生理解各个量之间的关系,从而分析并解决问题,达到事半功倍的学习效果。
那么,线段图在小学数学教学中的实际应用情况如何呢?
一、线段图在学生心目中的地位
人教版教材第一次正式介绍线段图是在三年级上册,本册一共出现两个用线段图来解决的问题:一个是“倍”的问题,另一个是“归总”问题。那么,对于这个学段的学生来说,线段图在他们心目中有着怎样的地位呢?笔者设计了一个调查表,对所教三年级的两个班共85位学生进行了调查,具体内容如表1所示。
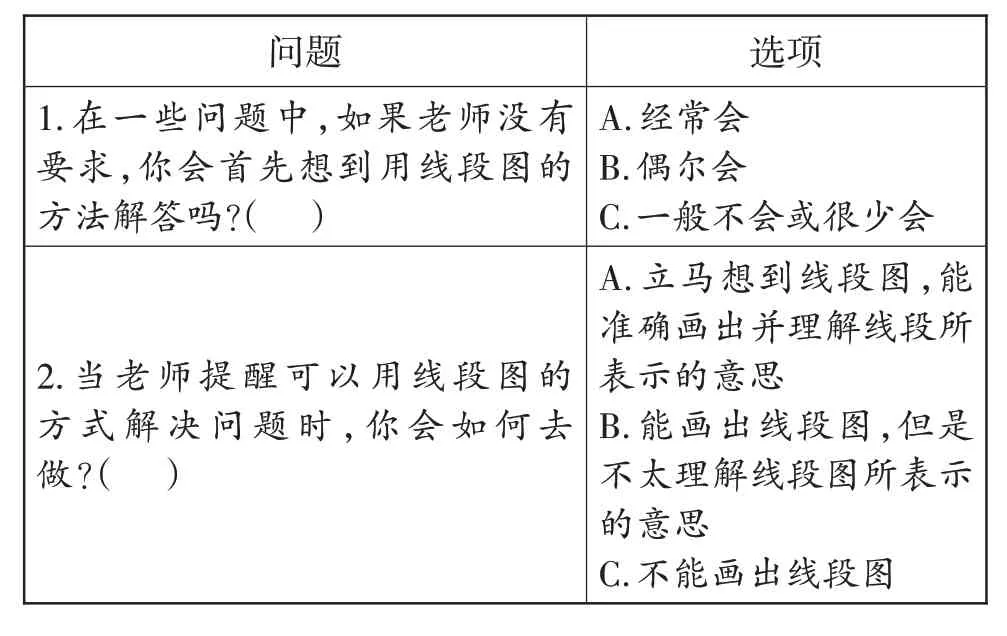
表1 利用线段图解决问题小调查
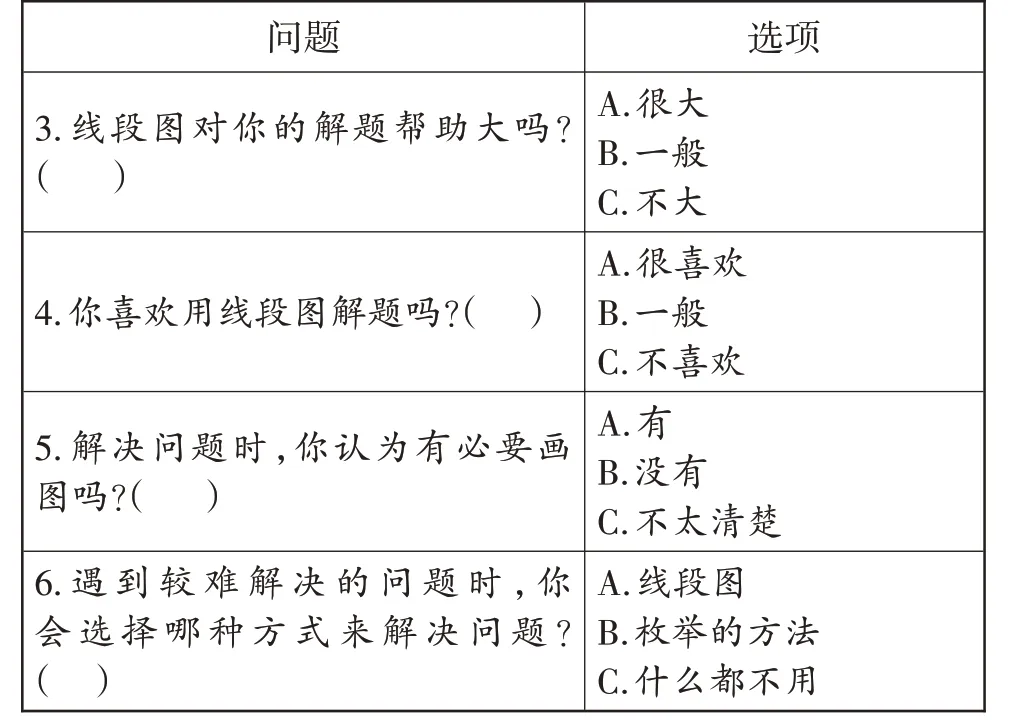
续表
调查统计结果如图1所示。
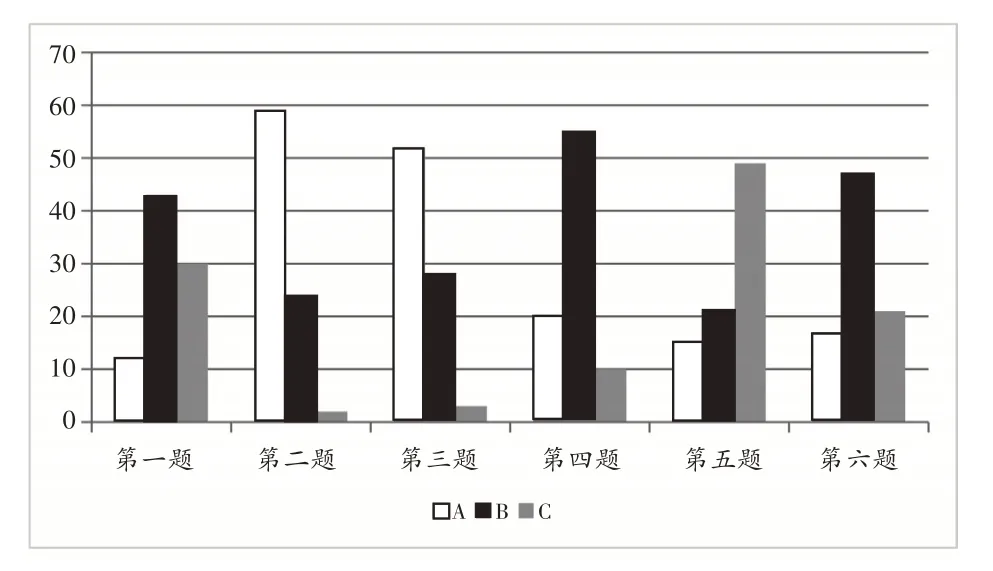
图1
从调查统计结果中可以看出,学生对于线段图有一定的了解,但还不够深入,不会灵活应用。很多学生在解决问题时如果教师事先没有要求利用线段图,很多学生在解决问题时很少会想到线段图。大部分学生在教师的提醒下能够画出线段图并能较好地理解线段图所表示的意思,由此可以看出,线段图在学生理解题意及解题上有很大的帮助。
二、线段图在“和倍问题”中的灵活应用
1.从“物”到“线”,发现“它”
从抽样调查结果可以看出,很多学生对于线段图有一种莫名的恐惧。想让学生真正利用线段图,首先要让学生做到不害怕,则需要让学生发现线段图其实就在身边,并且是常常见面的“老朋友”,只是它会穿上一件“实物”的外衣。比如,二年级上册第二单元“100以内的加法和减法”中的解决问题教学:如图2,一班得了12面小红旗,二班比一班多得3面。二班得了多少面?其中,实物“小旗”整齐的排列就有线段图的影子。类似这样的例子在一、二年级的数学教材中还有很多。

图2
将实物图慢慢转化成线段图,帮助学生从形象思维过渡到抽象思维。
【教学片段1】
出示:苹果的个数是梨的4倍。
师:你能用画图的方式表示它们之间的关系吗?
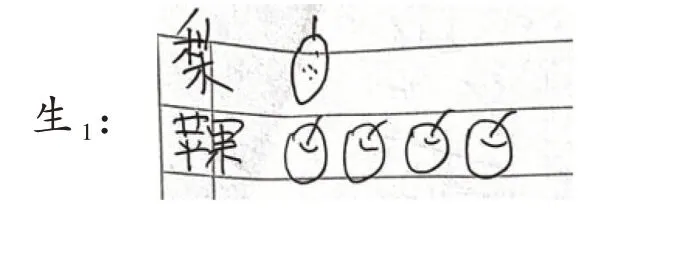
图3

图4
师:你们对这两位同学的表示方法有什么评价?
生3:这里没有告诉我们苹果的个数,感觉生2更加准确地表达了苹果和梨之间的关系。
师:两幅图之间是否存在联系?
生4:都表达了苹果的个数是梨的4倍。
教师把两幅图重合在一起:

图5
师(指着梨的部分):这里的梨除了是1个,还可以是其他个数吗?
生5:2个、3个……很多个。
师(指着苹果部分):如果梨的一小段表示2个,那么苹果的一小段表示几个?
生6:2个。
师:如果梨的一小段表示5个,那么苹果的一小段表示几个?
……
师:可见线段图从实物图而来,却又比实物图更简洁。
上述教学中,通过实物图与线段图的比对,让学生感知线段图与实物图之间的联系,明白线段图从实物图中来,却又比实物图更简洁。线段图中的一小段中可以表示1,表示2,以及更大的数,而实物图往往会有局限性。学生体会到线段图带来的便利,进而明白线段图的重要性。
2.一“线”多用,靠近“它”
很多时候,学生对于线段图这一解题工具的使用仅限于一道题,每每遇到新的情况,又会从头来思考。观察学生所画的线段图,还会发现一个现象,当数据大时,学生总喜欢把线段画得长一些,反之亦然,但实际上数据的大小与所画线段图的长短并没有关联。这些现象表明,学生显然对于线段图的实际使用还没有形成正确的认识。让学生正确理解和认识线段图是教学的重中之重。
【教学片段2】
出示:两筐苹果一共重35千克,第一筐是第二筐的4倍,第一筐苹果和第二筐苹果各有多少千克?
师:你能用画线段图的方法来解决这个问题吗?请大家画一画,算一算。
出示学生的线段图:

图6
出示学生的算式:
(1)35÷(1+4)=7(千克),35-7=28(千克);
(2)7×5=35(千克),35-7=28(千克);
(3)35÷5=7(千克)。
生1:第二筐画1段,而第一筐是第二筐的4倍,所以第一筐要画4段,每段就是35÷5。
师:5表示什么?
生2(上台边指线段图边讲):从图上来看,5就是1段加4段,第二筐有1段,第一筐有4段,一共就是5段,而5段对应的是35千克,所以35除以5就可以算出一段是多少。
师:大家听懂了吗?有不一样的想法吗?
……
师:同样的线段图,刚才表示苹果的个数是梨的4倍,现在表示两筐苹果。现在一段线段所表示的数是多少?
生3:7千克。
师:那么这样的线段图还能有其他的应用吗?
出示:班级里有科技书和音乐书一共72本,科技书是音乐书的3倍,科技书有多少本?
生4:现在我们只需要在原来的那条线段图上去掉一段就可以了。音乐书画1段,科技书画3段,一共就有4段。
师:现在一段线段又表示多少呢?
生5:18本。
师:同类型的线段图,帮助我们解决了3个问题。你能根据此类线段图自己编一道题考考大家吗?
上述教学中,通过对同类型线段图的重复利用,让学生根据给出的线段图自己创编题目,帮助学生进一步理解线段图的本质。可见,同一类型的解决问题能用相似的线段图来解决,帮助学生举一反三。
3.“线”“线”联系,理解“它”
要让线段图成为学生解决问题时的首选,就要挖掘线段图的内在优势,利用线段图进行创造性的学习活动。
【教学片段3】
出示题目:(1)教室里有科技书和音乐书一共72本,科技书是音乐书的3倍多4本,科技书和音乐书各有多少本?
(2)教室里有科技书和音乐书一共72本,科技书是音乐书的4倍少13本,科技书和音乐书各有多少本?
师:大家仔细观察一下,题目发生了什么变化?你还能解决吗?
(学生自主完成,集体交流)
师:题(1)中,一份表示几?
生1:17本。
师:题(2)中,一份表示几?
生2:17本。
师:仔细观察线段图(图略),你有什么发现?
生3:从线段图中可以看出,题(1)中多的4本和题(2)中少的13本正好能合成一份。
生4:科技书是音乐书的3倍多4本,等同于科技书是音乐书的4倍少13本。
师:你能根据该线段图自己编一组题考考大家吗?
上述教学中,利用两组线段图的内在联系,更好地帮助学生理解“和倍”问题,让学生感受这类问题是“线与线”之间的联系。同时,引导并放手让学生从自己的知识经验出发自主构建线段图,通过实践操作,感受线段图的直观、形象和实用,增强运用线段图的自主性。
综上,线段图可以直观地帮助学生分析题意,并简洁明了地标示出题中复杂的数量关系,进而开拓学生的数学思维。小学生的年龄特点和心理特点,使得小学生对要解决的问题理解并不是很透彻。问题中大量复杂的数量关系和文字叙述使学生产生畏惧心理。教师要让线段图真正用起来,真正“活”起来,培养学生的作图意识并不是一蹴而就的,需要在教学过程不断地渗透,在教学实践中积极探索,让学生在潜移默化中将线段图的应用落到实处。

