基于SEM-SD模型的终端区管制系统OEO
闫少华,于 琦,张兆宁
(中国民航大学空中交通管理学院,天津 300300)
1 引言
2018年,空管共保障航班起降架次突破1000万,创造了近9年来最好的航空运输记录。在保障航班起降架次数稳步提升的环境下,确保管制系统的安全、高效运行关系到整个空中交通管制服务的优劣。针对管制系统运行效率的问题,国外学者主要以空中交通管制的绩效为研究目标,通过分析经济性、安全性和飞行效率来间接反映管制系统的运行效率。国际民航组织在《空中航行系统的总体绩效手册》中规定了空中交通管制的11个绩效指标,其中包含效率、安全等,为今后的绩效量化评价提供了理论依据。Button等运用数据包络分析法对欧洲8年间的36个地区管制系统的经济效率进行比较,分析了空中交通管制服务的差异性会影响管制系统的经济效率。Reynolds通过航迹扩展和燃油效率分析飞行效率低下的原因,量化飞行效率,实现对空管系统绩效的量化分析。
国内有关管制系统的研究主要以质量、风险控制和效率为评估目标。张建平等将管制运行效率与空中交通流密度、运行安全性能及管制员负荷作为评估指标,利用BP网络模型对空中交通管制运行品质作出等级划分。张兆宁等提出基于过程的故障模式及影响分析方法,识别终端区管制系统潜在的风险因素,并将风险因素分为3类,通过其内部关系,有效的实现系统风险分析,间接提升管制系统的运行。张兆宁等建立加速遗传投影寻踪的终端区管制运行质量评价模型,进一步优化管制运行质量。中国民用航空局在《2017年全国民航航班运行效率报告》中,采用额外进近时间作为航班进近效率指标,为终端区管制运行效率评价提供了数据和理论基础。闫少华等通过折衷排序法对管制运行效率进行量化评估。
综上所述,目前对管制系统的研究集中于评估阶段,而管制系统是一个动态复杂反馈系统,单纯的评估存在着局限性,同时在评估结果上也缺少切实可行性建议,无法体现反馈机制的信息调节过程。本文在以往运行效率评估的基础上,构建SEM模型,分析影响终端区管制系统运行效率的主要因素,结合SD模型揭示复杂系统的反馈调节机制,借助Vensim仿真软件探究效率优化的理想解。利用SEM模型的静态评估与SD模型的动态反馈调节相结合,以期为终端区管制系统的运行完善提出可行性建议。
2 终端区管制系统运行效率的SEM模型
2.1 终端区管制系统运行效率分析
终端区是空中交通管服务的重要区域,由于终端区环境的复杂性和动态性,在安全的条件下。因此,识别影响管制系统运行效率的主要因素是提高效率的关键。国际民航组织(ICAO)在《全球空中交通管理的经营理念》(9854号文件)中指出空中交通管制系统是一个通过人、信息、技术、设施和服务的协同集成提供空中交通管理的系统,由空中、地面、通信、导航和监视相互支持作用。基于以上内容,本文选取资金投入、终端区饱和度、管制移交率、延误程度、管制员工作负荷和不安全事件作为影响管制系统运行效率的主要指标。将6个主要指标深入分析得出以下16个效率影响要素集,如表1所示。
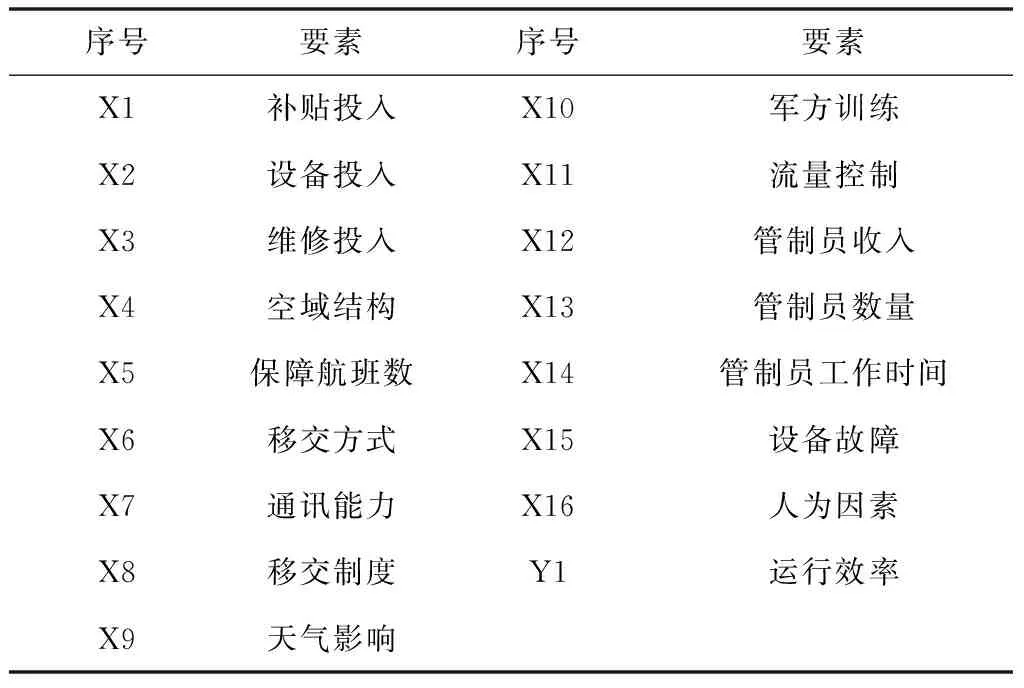
表1 管制系统运行效率影响要素集
2.2 问卷调查及样本概述
为了探究6个主要指标对运行效率的具体影响关系,采用问卷调查的方式验证以上指标之间的相互关系及合理性。将表1中的17个要素对应分配17个问题展开调查,问卷采取不同的分级,进行7级计分。研究选取某空管局一线工作的管制员为调研对象,共计观察变量17个,共发放问卷300份,回收到有效问卷295份,有效问卷回收数满足问题数10倍以上,回收率达到98.3%,因此所选取的样本能够较好的达到统计量需求。样本的数据信息统计如下表2所示。
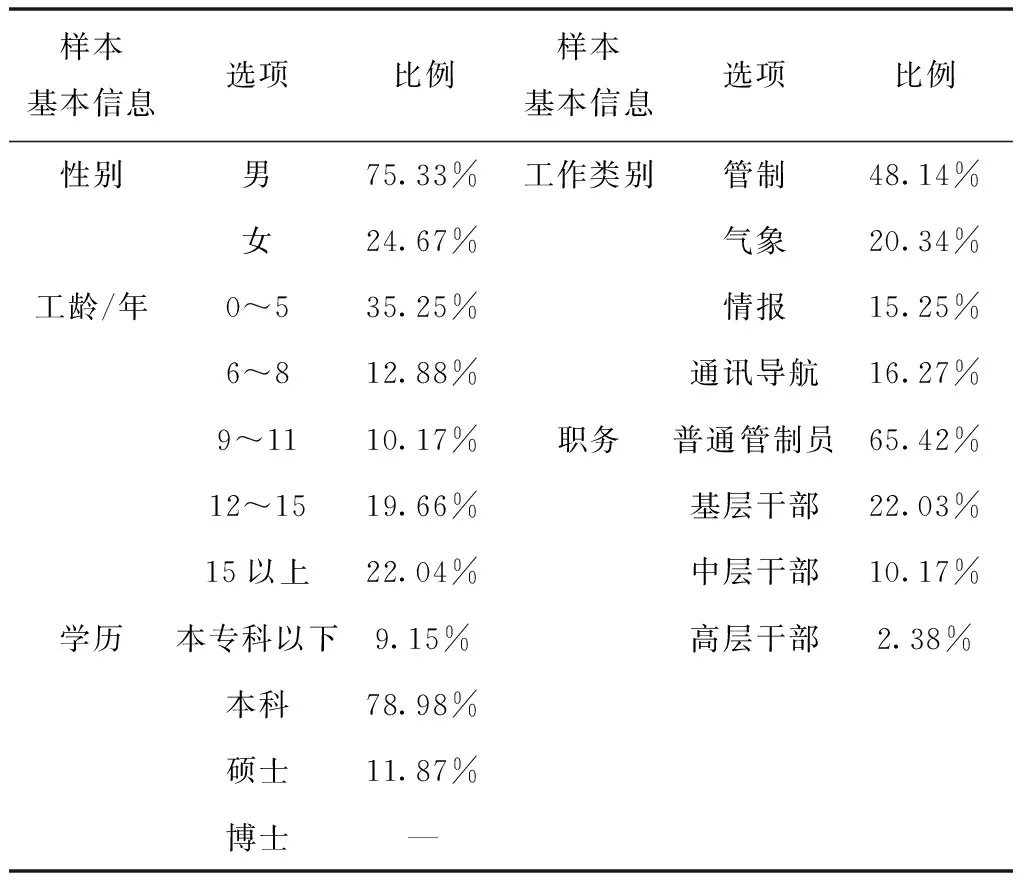
表2 样本数据信息统计
2.3 样本数据可靠性检验
样本数据的可靠性检验能够验证样本数据的准确性和真实性,而样本数据的可靠性检验包含信度检验和效度检验。本文采用克朗巴哈信度系数检验样本数据的信度,当克朗巴哈信度系数大于0.6时,认为样本具有很好的信度。通过SPSS23软件计算得到信度值如表3所示,可以看出克朗巴哈信度系数均大于0.6,说明样本数据的信度较好。通过表3可以看出KMO值均大于0.6,说明样本数据适合进行因子分析,且巴特利球型检验p值均小于0.01,故通过显著水平为1%的显著性检验。样本数据具有很好的效度。
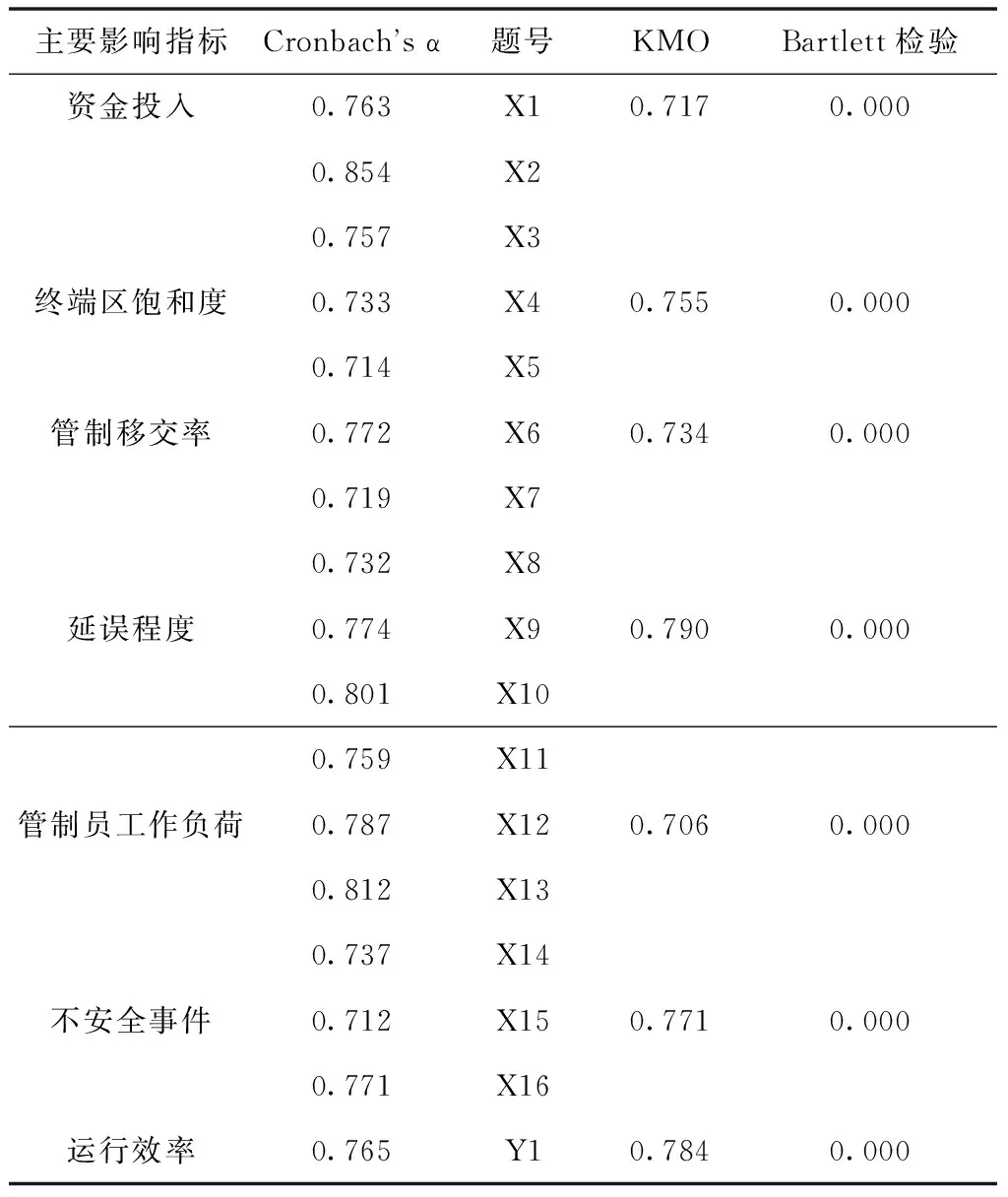
表3 可靠性检验结果分析
2.4 SEM模型的建立
为了研究6个主要指标对运行效率的具体影响程度,利用调查问卷中的数据结合AMOS26软件构建SEM模型,模型构建的好坏需要验证模型的拟合度,通过表4可以看出χ/df的值小于3,结果适配理想;RMSEA的值小于0.08,适配理想;GFI、AGFI、CFI的值均大于0.9,适配理想。IFI的值接近0.9,适配理想。整体来看,模型的结构较为合理。因此建立的SEM模型如下图1所示,SEM模型能处理涉及多个因变量的问题,且变量可以是不能直接测量的潜变量,并可对不同的理论模型进行评价,适合应用于本问题研究。

表4 拟合度系数
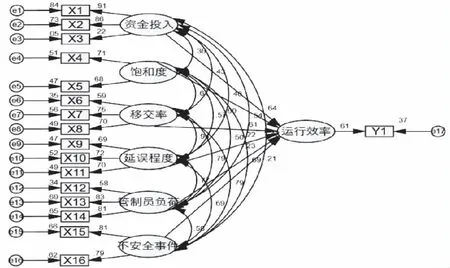
图1 终端区管制系统运行效率路径图

表5 终端区管制系统运行效率模型标准化路径系数
2.5 结果分析
通过表5中的结果,可以看出:(1)6个主要指标对运行效率的路径显著水平较高,说明了模型的可靠性较高。(2)从路径的标准化系数可以看出,资金投入、饱和度和移交率对运行效率具有正向影响,即增加资金的投入能从一定程度上提高运行效率,且资金投入对运行效率的正向影响略大于饱和度和移交率;延误程度、管制员负荷和不安全事件对运行效率具有负向影响,即随着延误程度的加剧,运行效率在一定程度上会下降,且延误程度和管制员负荷对运行效率的负向影响略大于不安全事件。
3 终端区管制系统运行效率的SD模型
3.1 模型的分析
在前文中将影响运行效率的主要指标分为两类,分别为正向指标和负向指标。由于终端区管制系统是一个随时间时刻变化的多回路动态复杂反馈系统,而SD模型是一种基于系统信息反馈思想和计算机仿真相结合的学科,通过系统的结构,构造因果关系模型,并利用反馈、调节和控制的原理,进一步实现系统的仿真分析。因此,为了探究两类主要指标对运行效率的具体反馈机制,结合SEM模型的静态分析结果构造终端区管制系统运行效率的SD模型。
3.2 模型的假设
为合理的研究系统的反馈调节机制和动态优化问题,在终端区管制系统运行效率的SD模型中提出如下假设。
假设1:终端区管制系统的运行效率由航班保障量、资金投入、终端区饱和度、管制移交率、延误程度、不安全事件和管制员负荷共同影响。
假设2:对管制系统的资金投入为保障航班资金投入数。
假设3:根据前文的结论,资金投入、饱和度和移交率对运行效率具有正向影响;延误程度、管制员负荷和不安全事件对运行效率具有负向影响。
假设4:资金投入、饱和度、移交率、延误程度、管制员负荷和不安全事件均为运行效率的表函数,且各个指标的权重以上文中的SEM模型结果为依据赋值。
3.3 终端区管制系统运行效率因果关系图
根据管制系统运行的机制和以上假设,构造的终端区管制系统运行效率因果关系图如图2所示。
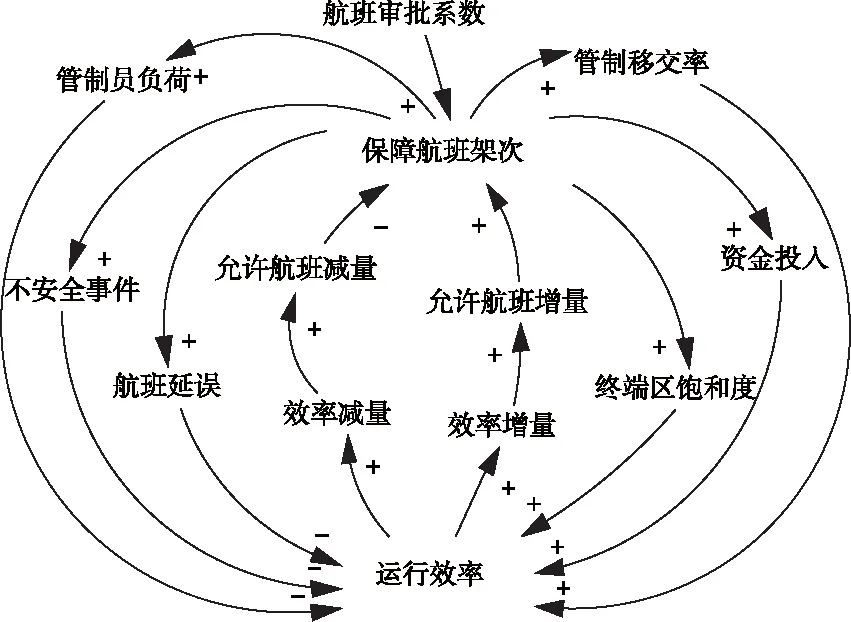
图2 终端区管制系统运行效率因果关系图
主要反馈路径如下:
路径1:保障航班架次↑ →资金投入↑ →运行效率↑ →效率增量↑ →允许航班增量↑
路径2:保障航班架次↑ →管制移交率↑ →运行效率↑ →效率增量↑ →允许航班增量↑
路径3:保障航班架次↑ →终端区饱和度↑ →运行效率↑ →效率增量↑ →允许航班增量↑
路径4:保障航班架次↑ →航班延误↑ →运行效率↓ →效率减量↑ →允许航班减量↑
路径5:保障航班架次↑ →不安全事件↑ →运行效率↓ →效率减量↑ →允许航班减量↑
路径6:保障航班架次↑ →管制员负荷↑ →运行效率↓ →效率减量↑ →允许航班减量↑
3.4 终端区管制系统运行效率流图
SD模型的核心是绘制流图和构造方程式,流图是因果关系图的进一步体现,能够再现管制系统的运行过程,反映管制系统各组成部分的相互影响关系。通过信息反馈的调节,识别管制系统的敏感性因素,更有效的实现效率模型的优化。本文采用Vensim仿真软件绘制终端区管制系统运行效率流图如图3所示。
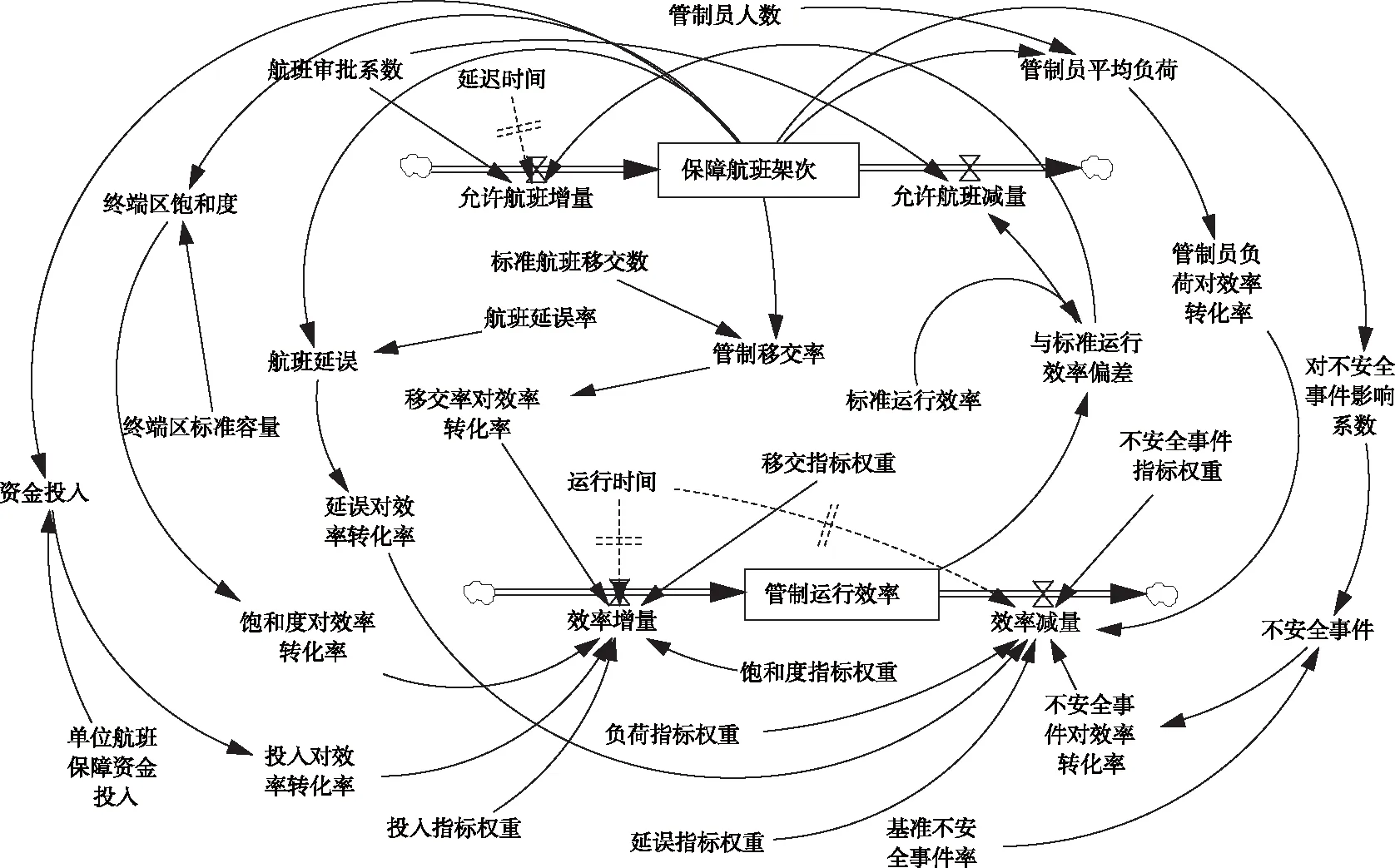
图3 终端区管制系统运行效率流图
模型中,保障航班架次的初始值根据郑州空管局2009年保障航班数37.09万架,航班延误率为0.25。运行时间参数值设置为1年,单位航班保障资金投入为0.3万元,基准不安全事件率为0.01。模型中的主要方程如下
X
=INTEG
(ΔX
-ΔX
,X
)(1)
Y
=INTEG
(ΔY
-ΔY
,0)(2)
ΔX
=DELAY
1(k
*IF
THEN
ELSE
(ΔY
>0,ΔY
,0),1,1)(3)
ΔX
=DELAY
1(k
*IF
THEN
ELSE
(ΔY
≤0,ABS
(ΔY
),0),1,1)(4)
ΔY
=DELAY
1(A
′*a
+B
′*b
+C
′*c
,1,0)(5)
ΔY
=DELAY
1(D
′*d
+E
′*e
+F
′*f
,1,0)(6)
A
=X
*α
(7)
B
*X/B
(8)
C
=X/C
(9)
E
=X
*β
(10)
F
=X/F
(11)
G
=G
*χ
(12)
ΔY
=1-Y
(13)
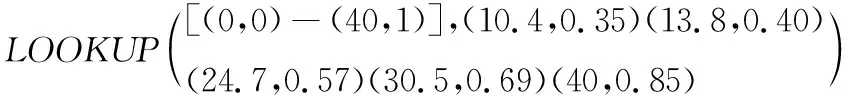
(14)
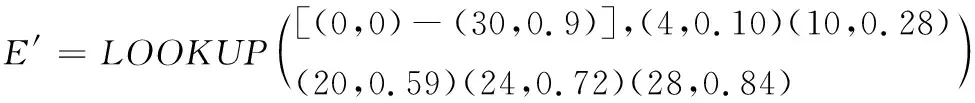
(15)
其中,X
为保障航班架次,Y
为管制运行效率,ΔX
、ΔX
分别为允许航班增量和允许航班减量,ΔY
、ΔY
分别为效率增量和效率减量。α
、B
、C
、β
、F
、χ
分别为单位航班保障资金投入、终端区标准容量、标准航班移交数、航班延误率、管制员人数和基准不安全事件率。A
、B
、C
、E
、F
、G
分别对应资金投入、饱和度、移交率、延误程度、管制员负荷和不安全事件,a
、b
、c
、e
、f
、g
分别对应各自权重,权重值由前文中SEM模型的结论经均值化得出a
=0.
4;b
=c
=0.
3;e
=f
=0.
35;g
=0.
3。3.5 模型检验
SD仿真模型的检验包括结构检验、量纲检验和拟合度检验,其中结构检验和量纲检验在Vensim软件运行中已经得到验证,本文采用郑州空管站2009年—2018年的实际年保障架次验证模型的拟合度,验证结果如表6所示。经验证,模型拟合度均在5%内。模型能够较好的反映实际情况。

表6 拟合度分析
3.6 敏感性因素识别
通过模型参数变化比较对影响分析结果的多少,如果变化参数对结果影响较小,则该参数为不敏感性因素,如果变化参数对结果影响较大,则为敏感性因素。
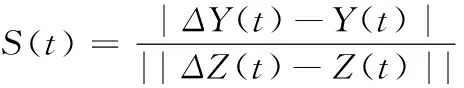
(16)
其中Z
(t
)为参数。通过计算得到终端区管制系统运行效率的敏感参数是单位航班保障资金投入、延误率和基准不安全事件率。说明可以通过调节以上3个参数值,达到效率优化控制。3.7 结果分析
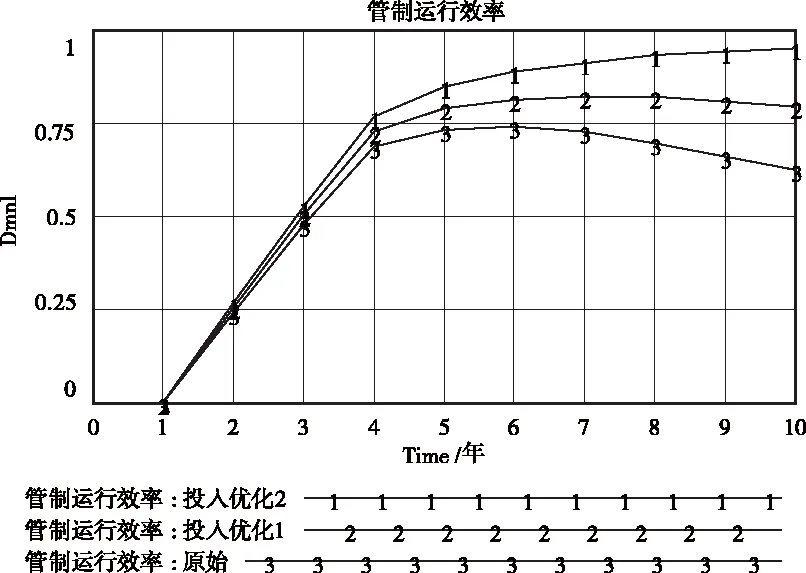
图4 投入对效率优化
通过Vensim软件分别输出敏感性因素对终端区管制系统运行效率仿真结果如图4、图5、图6所示。从图中结果可以得出以下结论:①终端区管制系统运行效率由于在模型刚运行的前两年有时间延迟,运行效率较低,故可忽略此影响,随着时间的推移运行,由于保障航班数由增多至容量过饱和等原因,导致运行效率趋势先稳定上升后呈下降趋势。②单位航班保障资金投入越高,终端区管制系统运行效率越高。单位航班保障资金投入由0.3万元增加到0.35万元时,运行效率有所提升;当资金投入增加至0.4万元时,运行效率达到最优化的理想结果。③延误率越低,终端区管制系统运行效率越高。当延误率由0.25降至0.2时,运行效率达到理想的优化值趋于稳定。④降低不安全事件率,可以有效的提高终端区管制系统运行效率。当不安全事件率由0.01降至0.005时,可以使运行效率的优化结果更显著。
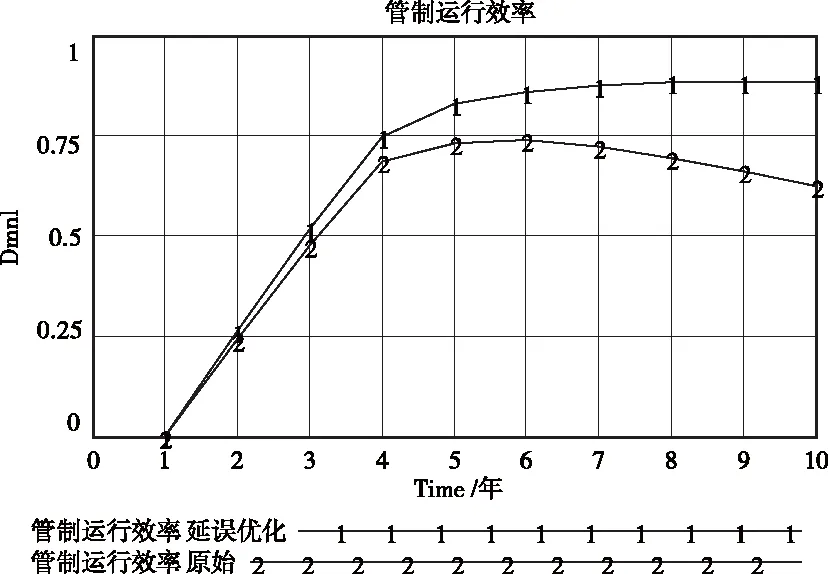
图5 延误对效率优化

图6 安全对效率优化
4 结论
本文在终端区管制系统运行过程的基础上,运用SEM模型静态识别管制系统运行效率的正向影响因素和负向影响因素,结合SD模型分析其动态反馈调节机制,通过Vensim仿真,在效率评估的基础上,提出具体可行的运行效率优化方案。仿真结果表明:增加保障航班的资金投入、控制航班延误率和降低不安全事件率可以有效的提升运行效率。本文为终端区管制系统运行的进一步完善提供了理论基础。

