一道基本不等式练习题的解法与赏析

◎鲍红志

(天津市武清区南蔡村中学，天津 301709)

“基本不等式”是从现实问题和实际问题中抽象出来的一个模型，是培养学生“数学抽象、逻辑推理、数学建模、直观想象和数学运算”等数学核心素养的极好素材

高中数学学习评价关注学生知识技能的掌握，更关注数学学科核心素养的形成和发展，制订科学合理的学业质量要求，促进学生在不同学习阶段数学学科核心素养水平的达成基本不等式作为求最值的一个重要的数学工具，运用起来非常方便我们在运用基本不等式的时候，一定不能疏忽“一正、二定、三相等”的基本要求在实际运用解决数学问题的时候，依据已知条件，难点是把代数式配凑成基本不等式的加法或者乘法的形式，把构建通过相加或者相乘运算出现定值作为基本方向本文通过一道题目，多角度巧妙运用“1”，充满了趣味性，也彰显了数学中“一题多解”的魅力每一道变式题目，都可以运用其他的“1”代换去解题依托基本不等式及已知条件，分析及解决问题的过程可以很好地培养学生的数学建模及逻辑推理的数学核心素养

高中数学中不缺乏好的题目一道好的题目，不仅可以让人耳目一新，同时让人爱不释手一道好的题目，不仅可以传授知识和方法，也可以培养学生的数学核心素养一道好的题目，不仅可以展示数学知识的“万般变化、紧密联系”，同时可以展现数学的“自然”之美一道好题总会给人留下很大的拓展空间，让你产生无尽的遐想

【解法1】 整体“1”代换

因为+=1，

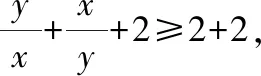
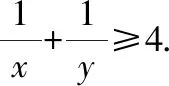
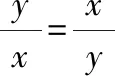
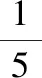
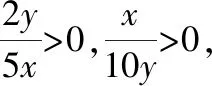
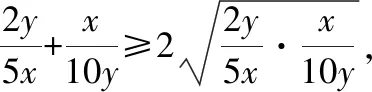
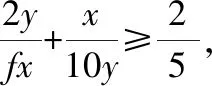
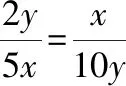
【启迪】形如：

这类问题求最值可以选择整体“1”代换其核心是“任何数(或者代数式)乘以1，还等于其本身”

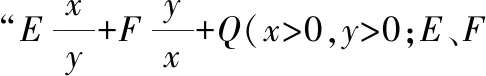
【解法2】 直接“1”代换

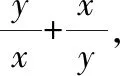
因为+=1，

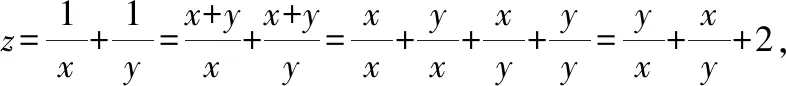
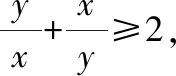
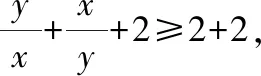
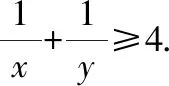
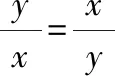
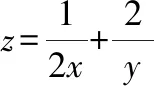
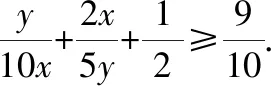
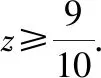
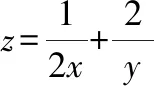
【启迪】 形如：

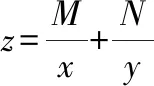
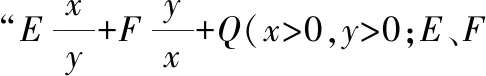
【解法3】 通分“1”代换

比较已知条件和所求代数式，如果对所求代数式进行通分处理，分子就是+，这样可以直接替换成1只需要求出分母的最大值即可由于,均为正数，它们的和+为定值1，并且当且仅当=时，等号成立可以利用基本不等式求的最大值解析过程如下：

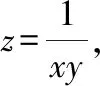
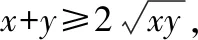
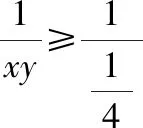
则≥4

由解法3的启示，对所求代数式进行通分整理，分子就是4+6，恰恰是2+3的2倍这样可以直接替换成1只需要求出分母的最大值即可需要注意的是正负号的问题及不等号方向的问题解析过程如下：

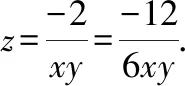
由于,都是正数，则2>0,3>0

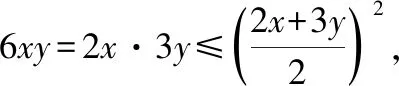
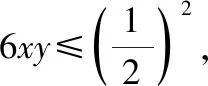
整理，得≤-48

【启迪】形如：

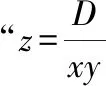
【解法4】已知条件巧用“1”

由解法3，可以联想到，已知条件满足基本不等式的使用条件，可以求出的最大值所求代数式通分整理，利用不等式性质，就可以求出的最小值解析过程如下：

由于,都是正数，根据基本不等式，

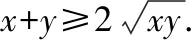
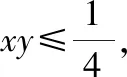
即≥4

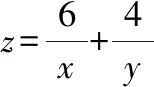
由解法4，已知条件2+3满足基本不等式的使用条件，可以求出的最大值所求代数式通分整理，利用不等式性质，就可以求出的最小值解析过程如下：

由于,都是正数，则2>0,3>0

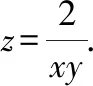
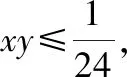
整理，即≥48

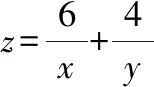
【启迪】形如：

课标用“经历(感受)、体验(体会)、探究”等刻画课堂教学活动细节的动词，概括了课堂教学中落实过程目标与方法目标的重要途径“过程与方法”是认知的杠杆，从“经历、体验到探究”，是“实践、认识、再实践、再认识”的循序渐进的过程，我们要将学生推到主动参与的位置，让他们经历这样的探索过程，才能提高他们的思维能力，同时培养他们的数学核心素养由此可见，数学学习的过程既是学生暴露思维活动、产生各种疑问的过程，也是他们在实践活动中经历、体验、探究知识、发展个性特长的过程

学习活动中，学生若不亲身经历一系列的观察、比较、分析、抽象、概括等数学认知活动，不经历多种观点的碰撞和争论，就难以获得基本不等式的各种证明方法如何让学生掌握证明方法，进而让学生真正理解其本质，应该从学生“最近发展区”——比较法开始让学生体验寻找数学规律的心路历程，体会数学思想方法，发展逻辑推理素养

对于高中生而言，老师在课堂教学活动中，如果能让学生更多地获得成功，更多地用平常心对待问题，心平气和地积极解决问题，有信心并能从容地面对学习和生活，才是我们教育教学的最好的意义所在，也是新时代教育的最高精神的体现由此可见，课堂教学的意义是非常重要的一堂好课，可以让人有收获感，可以让人心情愉悦；一堂好课，不仅可以让学生收获知识，还可以培养学生的核心素养；一堂好课，不是简简单单就能展示出来的，而是需要我们精雕细琢

课堂生成是预设的升华，是学生学习的顿悟但由于学生的年龄特点，在认知水平上有一定的局限性，课堂生成难免存在一定的偏颇和缺陷，这就需要教师引领和点拨对于创意的生成性资源，教师应适时调整预设方案，实现课堂教学活动的动态生成对于单一的生成性资源，教师可以通过追问的方式让学生的思维活跃起来对于存在偏颇的生成性资源，教师应因势利导，通过讨论、反思、纠错等方式引领学生回归正确的轨道，走向生成性课堂教学的新境界