以“经历—了解—知道—体会”为路径设计高中导数概念教学

◎方慧林 周学君* 孟岚 帅克伟

(1.黄冈师范学院 数学与统计学院,湖北 黄冈 438000；2.大冶市第二中学，湖北 黄石 435100；3.黄州思源实验学校，湖北 黄冈 438000)

一、引言

微积分是人类发展史中的一项伟大创造,是现代数学的一个起点近年来,美国、俄罗斯、中国等多个国家已将微积分列入了高中数学教材中,可见微积分在国际高中数学教学界受到了重视在中国,微积分的学习主要集中在大学阶段,为了使高中数学与大学数学有更好的衔接,2003年版的《普通高中数学新课程标准(实验)》中,将微积分直接命名为 “导数及其应用”,导数集数形于一体,具有很强的知识交汇功能,它衔接了高中数学中的多个章节内容《普通高中数学新课程标准(2017年版)》(以下简称《新课标》)在微积分中增加了数列极限、函数极限等内容,并对导数提出了更高的要求导数的概念不仅是大学数学的基础内容,而且在高中微积分的学习中处于特殊的地位

高中导数的教学一直是数学教育界的研究热点文献中对导数的教学研究主要分为导数应用的教学研究，导数解题技巧，“新、旧课标中” 对导数要求对比分析，《新课标》视角下导数教学研究等几个方面事实上,不少文献将研究重心放在了导数应用的教学研究上,且《新课标》实施以来,教学中加大了导数概念教学的研究然而,这些研究中对一线教师的导数教学的指导存在一定的局限性,这种局限性主要表现在将其直接应用于实践教学的可复制性、可操作性不强

《新课标》中对导数的明确要求有经历由平均变化率过渡到瞬时变化率的过程,了解导数概念的实际背景,知道导数是关于瞬时变化率的数学表达,体会导数的内涵与思想若严格以这四条要求 (即 “经历—了解—知道—体会” 的路径)为参考,那么教师在设计教学时的思路可以更加清晰,使得整个教学过程可以更加流畅高中生学习导数概念是比较困难的,但是他们按照此条路径循序渐进、逐步深入地学习,就不会存在畏惧心理

二、《新课标》对导数概念的要求

《新课标》对导数概念的要求是通过实例分析,让学生经历由平均变化率过渡到瞬时变化率的过程,了解导数概念的实际背景一般地,导数概念的学习起点是极限,但对于高中生目前的认知水平而言,他们理解极限的定义是较为困难的因此，在学生没有了解极限知识的情况下,老师可以创设一些情境来引入导数概念导数概念产生于实际问题中,所以在学习导数的概念之前,老师要让学生对导数的背景有所认识,学生在清楚导数的实际背景后就可以更好地理解导数的概念,掌握导数的相关知识在导数概念教学中,背景的选择尤为重要,为了使选择的实际问题与导数内涵相关,课本引入了瞬时变化率这一概念通过解决实际问题,以及建模的过程让学生感知平均变化率过渡到瞬时变化率的过程

《新课标》要求学生要知道导数是关于瞬时变化率的数学表达,体会导数的内涵与思想从教科书上的实际例子出发,可以激发学生学习数学的兴趣，增强学生学好数学的自信心,从而让学生能真正地理解导数的本质是瞬时变化率,并且知道导数是关于瞬时变化率的数学表达,体会导数的内涵老师在导数概念的教学过程中,首先利用数学建模思想,让学生通过实际例子建立模型,然后借助特殊到一般的数学思想,让学生知道导数表达式利用数形结合的思想,使用函数中的切线这一概念,借助割线逐渐 “逼近” 形成切线的过程让学生更加直观地理解导数几何意义,体会导数中的极限思想

三、导数概念的教学设计

《新课标》对导数概念教学的要求有四点,本节按照《新课标》的四条要求(即 “经历—了解—知道—体会”的路径)设计教学

(一)经历由平均变化率过渡到瞬时变化率的过程

首先让学生观看一段高台跳水的视频,当运动员与跳台一样高时,此时位移为0学生通过观看视频会有视觉上的感受,这样也能更加直观地思考以下问题:在高台跳水中,运动员相对于水面的高度(单位:m)与起跳后的时间(单位:s)存在函数关系

()=-49+48+11，

(1)

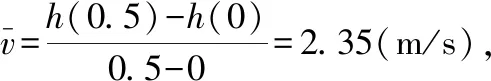
(2)

在1≤≤2时间内,

(3)

(1)运动员在此时间段内静止吗？

(2)你认为用平均速度描述运动员的运动状态合理吗？

探究过程:让学生学会利用数形结合的思想进行探究

()=-49+48+11，

(4)

结合函数图像()可知,

1.2.2 检测方法 两组患者手术前后次日早晨空腹抽取5 ml静脉血，离心8 min，速度为3 000 r/min，采用电化学发光法测定血清孕酮水平；采用酶联免疫吸附试验法测定VEGF和INH-A水平[12-13]。

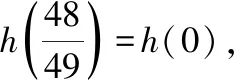
(5)

(二)了解导数概念的实际背景

《新课标》在导数概念的教学中,要求学生要了解导数概念的实际背景导数概念的形成过程具有一定的文化背景,通过对导数概念的深入学习,可以让学生对其产生浓厚的兴趣教师采用 “故事导入” 的方式讲授,先由一些人文故事吸引学生的注意力和兴趣,然后慢慢引导学生了解导数概念产生的一些实际背景,让学生知道导数这一概念的产生是为了解决生活中的实际问题

老师以讲故事的形式开始引入,例如:微积分有着一段相当漫长的历史,早在两千多年前,研究数学和力学的科学家,阿基米德在《圆的测量》著作的论述中就蕴含着微积分的思想刘徽在他的割圆术中提到“割之弥细,所失弥小,割之又割,以至于不可割,则与圆周和体而无所失矣”这些例子中描述的都是很典型的极限概念到了17世纪,随着数学和物理的快速发展,科学家们遇到的问题主要有以下几种类型:第一类是研究运动中的某时刻的速度问题;第二类是求曲线的切线问题;第三类是求函数的最值问题;第四类是求曲线长、曲线围成的面积，以及曲面围成的体积的问题针对这些问题,数学家们做了大量研究,这也为后面牛顿和莱布尼茨创立微积分打下了基础在17世纪下半叶,导数才真正被人们所了解,牛顿和莱布尼茨在这个时期是主要的代表人物牛顿在研究变速运动的物体在某个时刻的瞬时速度的实验过程中,发现了无穷小元素;莱布尼茨从几何的角度入手,提出曲线的切线就是连接曲线上无限接近两点的直线

故事讲完后,老师开始归纳与导数概念相关的内容众所周知,数学是来源于生活的,导数也不例外从导数的发展史来看,我们可以知道导数概念的提出是与生活中实际问题息息相关的,我们不难发现微积分的四类问题是从物理学和数学问题中衍生出来的,都是生活中实际的问题,导数概念的提出，正是源于解决这些实际问题的需要

(三)知道导数是关于瞬时变化率的数学表达

学生在了解导数是关于瞬时变化率的数学表达的过程中,经历了建模、抽象、归纳这几个步骤,本节将对这几个步骤进行详细设计

1建立模型

教材首先创设问题情境，从变化率引入导数的概念,从“高台跳水” 和 “抛物线的切线”两个例子出发,让学生感知了从平均变化率到瞬时变化率的转化过程,经历了由割线斜率过渡到切线斜率的过程

对于前述的高台跳水函数,探究如何求运动员的瞬时速度教师先考察=1附近的情况,让学生以小组合作的方式计算教材中的每个时间间隔的平均速度,得到结果如表1所示

表1 运动员在某段时间内的平均速度

(6)

为了使学生对导数的了解更加透彻,教师可以引入一个几何例子设曲线是函数=()=的图像,在曲线上取一点(1,1)及在点附近任取一点(,),连接,两点如图1,让学生观察,当点沿着曲线逐渐向点接近时,观察割线将绕着点逐渐转动(多媒体显示动画)

图1 割线与切线的演变关系

当点沿着曲线无限接近于点，即趋近于0时,如果割线(虚线)有一个极限位置,那么该直线叫作曲线在点处的切线割线的斜率的极限,就是曲线在点处的切线的斜率,则有的切线的斜率是

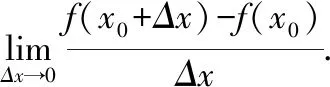
(7)

学生通过动手实操及观看动画,可以更加直观、深刻地理解导数的本质学生在说明自己的观点后,教师可以利用数学语言总结,这也充分体现了在教学中学生的主体地位,以及教师的主导地位

2抽象概念

教师讲透实例的具体内容,抽象出导数的定义,这样学生就很容易接受现用=()来表示高台跳水的函数,以及这里要指出的是在定义中

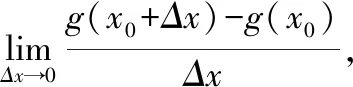
(8)

学生用更加直观的数据体会 “逼近”方法定义的导数,通过分析这两个实例,从而解决问题由式子(7)和(8)不难发现这两个问题的答案有一样的表示形式,现将这种形式用一般的形式表示出来

(9)

叫作函数=()从到+的平均变化率

3归纳定义

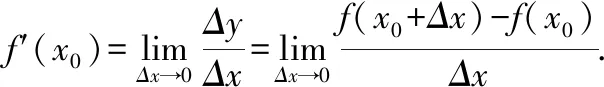
(10)

学生通过这两个实例,能够了解平均变化率和瞬时变化率的含义然后分析这两个不同的问题,能够发现每个题的解题答案的表达形式是相同的,从而把两个问题及解决方法转化为一般的形式,就可以得到平均变化率和瞬时变化率的表达式在学习本节课的引入部分,学生在开始就了解到了导数是一种极限的思想,那么从上述式子中就可以发现导数就是瞬时变化率的数学表达式

(四)体会导数的内涵与思想

学生在学习导数概念的这一过程中，可以感受到特殊到一般、数学建模及数形结合的思想

在得到导数概念的教学过程中,体现出了特殊到一般的数学思想从两个例题可以看出,一类是物理学中的平均速度和瞬时速度的问题,另一类则是几何学中割线和切线斜率的问题人们对新一类的事物的认识一般都是从这类事物的个体开始的,通过对某些个例的认识与研究,逐渐积累对这类事物的了解,从而发现规律,总结规律,这也就是特殊到一般的思想在本节教学中,针对两类不同的领域问题，最后答案的形式是统一的,可以将这种特殊形式抽象为一般形式的过程中,让学生感受到由特殊到一般的过程的思想方法

导数概念的数学表达式,是在解决实际问题的过程中产生的,这一过程中离不开数学建模的思想在导数的教学中,学生已经了解了导数概念的实际背景,并且知道了导数是关于瞬时变化率的数学表达得到导数的数学表达式的过程,实际就是一个数学建模的过程,“高台跳水”就是一个实际问题,然后再根据课本上的问题,以学生为主体,老师引导学生建立一个数学模型并对其求解在本节教学设计中，老师通过引导学生建立模型并求解,从而得到了导数的数学表达式,在解决这一实际问题时,学生全程参与了建模的过程,并在其中感受到了数学建模的思想

关于求抛物线的切线的问题,是一个抽象的问题,所以在这部分的教学中需要采用数形结合的形式针对切线这一板块的学习,学生的兴趣较高,但学生在数学语言的表达及数形结合的能力上仍有不足学生仅仅通过观察曲线的割线的变化趋势就得出导数的几何意义是比较困难的,但是目前越来越多的现代技术被应用在教学中,所以此时可以利用多媒体动态演示割线逼近切线的过程,既可以让学生了解无限逼近的思维模式,又可以让学生更加透彻地理解导数的几何意义

四、结语

导数是微积分中最重要、最基本且含意深刻的概念之一利用导数方法可以更好地研究初等函数的性质,加深学生对函数本质的理解本文基于《新课标》中对导数概念教学的四条要求(即 “经历—了解—知道—体会” 的路径)展开研究首先阐述了《新课标》对导数的教学要求然后针对每一个要求提出具体的教学设计的建议,通过视频,让学生从视觉上经历由平均变化率过渡到瞬时变化率的过程;借助导数的发展史,从导数的历史背景过渡到实际例子中,从而让学生了解导数概念的实际背景;通过课本上的两个例题的答案,抽象出了一个一般式,从而让学生知道导数是关于瞬时变化率的数学表达;在导数概念的教学过程中,让学生体会到由特殊到一般、数形结合及数学建模的思想本文是严格按照《新课标》要求(即 “经历—了解—知道—体会” 的路径)设计教学,研究视角新颖,为高中教师教授导数概念提供了可操作性、可复制性的教学思路