一类分数阶计算机病毒模型的稳定性分析

周学勇，路振国，程晓明

(信阳师范学院 数学与统计学院， 河南 信阳 464000)

0 引言

计算机病毒(Computer Virus)是一种人为编制能够对计算机正常程序的执行或数据文件造成破坏，并且能够自我复制的一组指令程序代码[1]。计算机病毒具有极大的破坏性、不可预测性等特点，已成为互联网安全的最大威胁[2]。建立计算机病毒传播的数学模型，揭示计算机病毒的发展趋势，进而找到计算机病毒预防和控制的策略等对于抵御计算机病毒的侵害、维护良好的网络安全和信息安全是非常有必要的。近年来，人们发现黏弹性模型[3]、计算机病毒传播模型[4]等许多问题用Caputo分数阶导数[5-6]来描述比较合适。本文将基于PIQUEIRA等[7]研究的一类网络病毒传播模型，建立Caputo分数阶SIRA计算机病毒模型(1)，来研究计算机病毒的传播特点。

(1)

其中：S(t)、I(t)、R(t)、A(t)分别表示t时刻易感计算机、感染计算机、临时免疫计算机、永久免疫计算机的数量；参数N、a1、a2、β,μ、σ、δ均是正数。N表示外部计算机连入网络的速率；a1(a2)表示易感计算机(感染计算机)采取杀毒防护措施直接转为永久免疫型计算机的概率，即永久免疫率；β表示病毒发生率；μ表示淘汰率；σ表示重复感染率；δ表示临时免疫率，0<α≤1。

模型(1)的初值条件为

S(0)=S0≥0,I(0)=I0≥0,

R(0)=R0≥0,A(0)=A0≥0。

(2)

1 主要结果

本节给出模型(1)解的非负性、有界性，计算出平衡点的表达式并讨论其稳定性。

1.1 非负性和有界性

由文献[5]知，模型(1)满足初值条件(2)的解是存在唯一的。

定理1 假设G(t)=(S(t)，I(t)，R(t)，A(t))是模型(1) 满足S(0)=S0>0，I(0)=I0>0，R(0)=R0>0，A(0)=A0>0的任意一个解，则对任意的t>0，都有S(t)>0，I(t)>0，R(t)>0，A(t)>0。

证明假设R(t)在(0，∞)不是非负的，则存在t>0，使得R(t)<0，令t*=inf{t:R(t)<0}，那么R(t*)=0，R′(t*)<0。由模型(1)的第三个方程知R′(t*)=δI(t*)<0,则I(t*)≤0。

若对任意的t>0,有I(t)>0，则产生矛盾；若存在t>0,使得I(t)<0，令t*=inf{t:R(t)<0}，则I(t*)=0，I(t*)<0。于是有下列两种情况：

(i)当t*≤t*时，得到I(t*)<0,产生矛盾；

(ii)当t*>t*时，得到I′(t*)=0，也产生矛盾。

由此可知，当t>0时，I(t)≥0，R(t)≥0。 显然，当I(t)=0时，DαI(t)=0；当R(t)=0时，DαR(t)≥0。 因此，对于所有的t>0，如果I(t)=I0>0，R(t)=R0>0，那么对于任意的t>0,有I(t)>0，R(t)>0。同理，当t>0时，S(t)≥0，A(t)≥0。显然，当A(t)=0时，DαA(t)=0;当S(t)=0时，DαS(t)=N+σR(t)≥0。因此，对于所有的t>0，若有S(t)=S0>0，A(t)=A0>0，则对于任意的t>0，有S(t)>0，A(t)>0。 证毕。

定理2 模型(1)所有满足初值条件(2)的解是有界的。

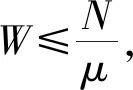
1.2 平衡点的存在性

令DαS=0，DαI=0，DαR=0，DαA=0。模型(1)可能存在4个平衡点：

(b)当Na1>μ2时，模型(1)存在平衡点E2(S2，0，0，A2)，其中

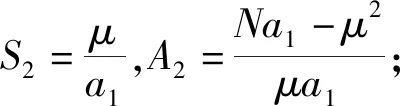
(c)当Nβ>μ(δ+μ)时，模型(1)存在平衡点E3(S3，I3，R3，0)，其中

(d)当μ2(β+a2)>a1(Na2+δμ+μ2)，(β+a2)(σ+μ)>a1(σ+δ+μ)，βS4>δ+μ时，模型(1)存在正平衡点E4(S4，I4，R4，A4)，其中

这里

F1=(β+a2)(σ+μ)-a1(σ+δ+μ)，

F2=μ2(β+a2)-a1(Na2+δμ+μ2)。

1.3 局部稳定性

本节分别研究平衡点E1、E2、E3、E4的局部渐近稳定性。

其中:

证明模型(1)在平衡点E1处的特征方程为

(3)

由方程(3)知，模型(1)在平衡点E1处有两个负特征值λ1=-μ，λ2=-(σ+μ)。 其余两个特征值为

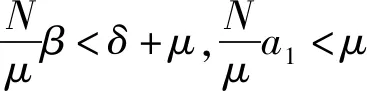
因此平衡点E1是局部渐近稳定的。

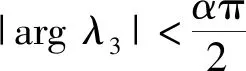
因此平衡点E1是不稳定的。证毕。

定理4 当βS2a1(S2-A2)时，平衡点E2是局部渐近稳定的；否则，平衡点E2是不稳定的。

证明模型(1)在平衡点E2处的特征方程为

(λ+a2A2-βS2+δ+μ)(λ+

σ+μ)[λ2+(a1(A2-S2)+2μ)λ+

μa1(A2-S2)+μ2]=0。

(4)

由方程(4)知，模型(1)在平衡点E2的特征值为

λ1=-(σ+μ)<0，λ2=-μ<0，

λ3=βS2-(a2A2+δ+μ)，

λ4=-μ-a1(A2-S2)。

当βS2a1(S2-A2)时，λ3<0,λ4<0。此时特征值满足

平衡点E2是局部渐近稳定的。

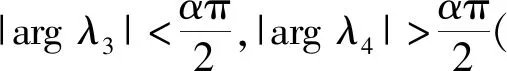
接下来,研究平衡点E3的稳定性。模型(1)在平衡点E3处的特征方程为

(λ-a1S3-a2I3+μ)(λ3+m1λ2+

m2λ+m3)=0，

(5)

其中:

m1=σ+2μ+δ+βI3-βS3，

m2=(σ+μ)(μ+δ+βI3-βS3)+

(βI3+μ)(μ+δ-βS3)+β2S3I3，

m3=(σ+μ)[(βI3+μ)(μ+δ-βS3)+

β2S3I3]-σδβI3。

当a1S3+a2I3>μ时，特征值

λ1=a1S3+a2I3-μ>0，

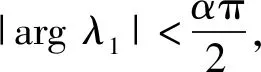
当a1S3+a2I3<μ时，特征值λ1=a1S3+a2I3-μ<0。平衡点E3(S3，I3，R3，0)的稳定性由下列方程确定:

P(λ)=λ3+m1λ2+m2λ+m3=0。

记

18m1m2m3+(m1+m2)2-

利用文献[8]得到如下结论：

定理5 假设a1S3+a2I3>μ且E3(S3，I3，R3，0)存在，

(i)如果D(P)>0，m1>0，m3>0和m1m2>m3，那么对所有的α∈(0，1)，平衡点E3是局部渐近稳定的；

(iii)如果D(P)<0，m1>0，m2>0，m1m2=m3，那么对所有的α∈(0，1)有平衡点E3是局部渐近稳定的。

下面研究正平衡点E4(S4，I4，R4，A4)的稳定性。正平衡点E4(S4，I4，R4，A4)处的特征方程为

Q(λ)=λ4+n1λ3+n2λ2+n3λ+n4=0，

其中:

n1=a1S4+a2I4+βS4-a1A4-4μ-

βI4-a2A4-δ-σ，

n2=(βS4-βI4-a1A4-a2A4-

2μ-δ)(a1S4+a2I4-σ-2μ)-

(a1A4+βI4+μ)(βS4-a2A4-δ-μ)-

(σ+μ)(a1S4+a2I4-μ)+

n3=(βS4-a2A4-δ-μ)(σ+μ)(a1S4+

a2I4-a1A4-βI4-2μ)+

(a1A4+βI4+μ)(a1S4+

a2I4-μ)(βS4-a2A4-δ-σ-2μ)+

a2I4-μ)-δσ]-a1A4[βa2S4I4+

a1S4(βS4-a2A4-δ-μ)]+

n4=βI4(a1S4+a2I4-μ)[δσ+

β(σ+μ)S4]-a1A4(σ+μ)[βa2S4I4+

a1S4(βS4-a2A4-δ-μ)]+

(a1A4+βI4+μ)(σ+μ)[(βS4-a2A4

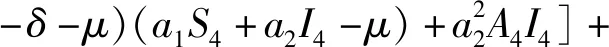
βa2I4A4(a1A4+βI4+μ)(σ+μ)+

σδa1a2A4I4。

记

(6)

由文献[9]可得下面结果。

定理6 假设E4(S4，I4，R4，A4)存在，

(i) 若u1、u2、u3是Routh-Hurwitz判别式，其中:

则当α=1时，条件

u1>0，u2>0，u3=0，u4>0

(7)

满足时，正平衡点E4是局部渐近稳定的。

(v) 平衡点E4是局部渐近稳定的必要条件是u4>0。

注1 对所有的α∈(0,1)，条件(7)是平衡点E4(S4，I4，R4，A4)局部渐近稳定的充分而非必要条件。

2 数值模拟

为了验证理论结果的正确性，采用Adams-Bashforth-Moulton(ABM)预测-校正算法对模型进行数值模拟。 为了用该算法给出近似解，考虑以下非线性分数阶微分方程[10-11]:

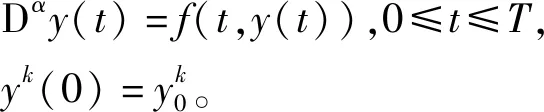
(8)

方程(8) 等价于下列积分方程：

(9)

其中，m=[α]。

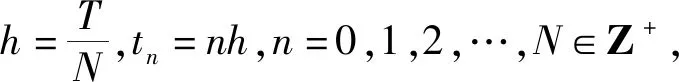
βSjIj-μSj+σAj)，

a2AjIj-δIj-μIj)，

a2AjIj-μAj)，

其中:

βSjIj-μSj+σAj)，

a2AjIj-δIj-μIj)，

σRj-μRj)，

a2AjIj-μAj)，

aj,n+1=

(n-j)α)，0≤j≤n。

限于篇幅，这里仅给出E4局部渐近稳定的情况。选取N=0.8，a1=0.025，a2=0.25，μ=0.2，σ=0.8，δ=0.4，β=0.5，初值为(S(0)，I(0)，R(0)，A(0))=(1.5，0.5，0.2，1)，通过计算得模型存在3个平衡点E1(4，0,0,0)、E3(1.2，2，0.8，0)、E4(1.846，0.615，0.246，1.292)。由模型(1)的时间序列图(图1)可知，模型(1)的解均趋向于平衡点E4，这说明E4是局部渐近稳定的。

图1 正平衡点E4存在情况下模型(1)的时间序列图Fig. 1 Time series of system (1) when the positive equilibrium E4 exists

3 结语

建立了一类Caputo意义下的分数阶网络病毒传播的SIRA模型，证明了模型(1)满足初始条件(2)的解是存在唯一的且正有界的；在一定条件下，给出模型(1)的平衡点表达式；讨论了模型(1)所有的平衡点的局部渐近稳定性。 最后，采用Adams-Bashforth-Moulton的预测-校正迭代算法给出了模型(1)的数值解，数值模拟结果验证了理论分析的正确性。 从图1可以看出,对于不同的α值，曲线上升和下降速度不同。但是，随着时间的推移，α大小不同的曲线最终都趋于稳定。 另外，当其他参数固定不变，而把感染率β降低到一定值时，数值解显示感染计算机、临时免疫计算机、永久免疫计算机数量经过一段时间后都将趋于0， 即计算机病毒传播得到有效控制。