3X+1迭代数列的几个性质

吴拿达

（韩山师范学院 数学与统计学院，广东 潮州 521041）

洛塔尔·科拉茨在20世纪30年代提出“科拉茨（Collatz）猜想”，它有多个不同的名称：3X+1猜想、角谷猜想、西拉古斯（Syracuse）猜想、冰雹猜想.这个猜想的内容是：给定任何一个正整数，若它是偶数则除以2，若它是奇数则让它乘3再加上1，按照这种规则不断地重复计算下去，最终会得到1.例如考虑奇数7，按上述规则变换依次如下：数学家已利用计算机验算到很大的数都满足猜想，但3X+1 猜想至今仍未被完成证明，吸引着众多的数学家和数学爱好者去攻克它.虽然直接攻克它很难，但是长期以来，学者们还是围绕它做了不少相关研究，这些研究大致可分三种类型.第一种类型就是给出接近的证明，在这方面最有代表性的工作是菲尔兹奖获得者陶哲轩于2019 年在ArXiv 和其博客上发表的结果［1］，证明3X+1 猜想对几乎所有的正整数都成立，但陶哲轩自己也承认把“几乎所有”变成“所有”还有巨大的鸿沟要跨越.第二种类型的工作是针对猜想的一些算法与计算研究，例如文献［2］就是这方面的代表作，文献［3］则进一步考虑计算需要的一些硬件条件的改进.第三种类型的工作就是对3X+1 猜想进行各种转化，获得与猜想密切相关的一些概念，然后对这些相关内容做进一步的研究，以期获得解决猜想的契机，例如文献［4］定义了3X+1 猜想的等价集，并以此给出3X+1 猜想的一个等价命题，文献［5］则对与3X+1 猜想密切相关的一些代数概念进行深入研究.本文的研究也属于第三种类型，为此，先介绍相关的一些概念.

对任意一个正奇数x0，设

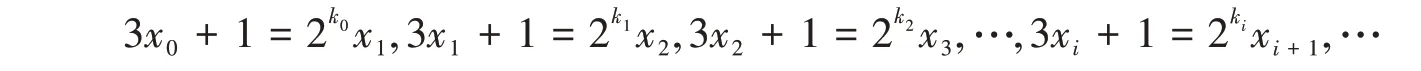
其中k0，k1，...，ki，...，x1，x2，...，xi，...都为正整数.称上述数列{xn}n>=0为x0的3X+1 迭代数列.若存在正整数N，使得对任意i>N，都有xi=1，则称x0回归于1，否则称x0不回归1.例如，

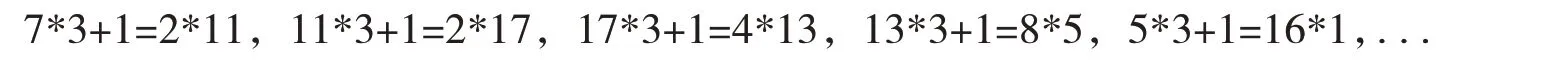
所以，7回归于1，其3X+1迭代数列是{7，11，17，13，5，1，1，....，1，...}.

根据上面的概念，显然“3X+1猜想”与下面两种表述等价［6］：

（1）所有的正奇数都回归于1;

（2）任意正奇数的3X+1迭代数列从某项开始恒等于1.

探寻正奇数的3X+1 迭代数列性质对最终解决该猜想可能会有积极的意义，而这正是本文要重点研究的内容.

首先利用组合数学中一类非齐次线性递推关系的求解理论来证明本文的主要结论之一定理1.为此，下面先列出几个相关引理.

特别当t=k,e1=e2= …=ek= 1, 此时递推关系的通解是un=++…+.

1.10 Western blot检测心脏组织中 IL-17、RORrt、IL-10、Foxp3蛋白表达 取出保存好小鼠心脏组织添加蛋白裂解液研磨，离心后收集上清液，采用蛋白提取试剂盒提取总蛋白，BCA试剂盒测定蛋白总浓度，SDS-PAGE电泳结束后，凝胶转移至PVDF膜上行转膜反应，添加5%脱脂牛奶室温下封闭1 h清洗后，加入一抗，4℃过夜，TBST清洗后滴加羊抗鼠IgG二抗，TBST清洗后ECL发光，置于凝胶成像仪中观察蛋白表达情况。

引理2（［7，定理3.16］）.若un=Bn是常系数线性齐次递推关系un=a1un−1+a2un−2+ …+akun−k(n≥k)的 通 解，un=bn是 常 系 数 线 性 非 齐 次 递 推 关 系un=a1un−1+a2un−2+ …+akun−k+f(n)(n≥k)的一个解（其中f(n)是以非负整数n为自变量的实函数），则un=Bn+bn(n为非负整数)是该常系数线性非齐次递推关系的通解.

引理3（［7，定理3.17］）.若1 是常系数线性齐次递推关系un=a1un−1+a2un−2+ …+akun−k(n≥k)的i重特征根（i为非负整数），f(n)是非负整数n的m次多项式，则常系数线性非齐次递推关系un=a1un−1+a2un−2+ …+akun−k+f(n) (n≥k)有形如un=nig(n)的特解，其中g(n)是n的一个m次多项式.

下面给出定理1并利用上述几个引理加以证明.

推论1若y0是正奇数，{yn}n≥0是y0的3X+1迭代数列，则{yn}n≥0不是严格单调递增数列.

推论2若y0是正奇数，{yn}n≥0是y0的3X+1 迭代数列，则对任意非负整数N，{yn}n≥N不是严格单调数列.

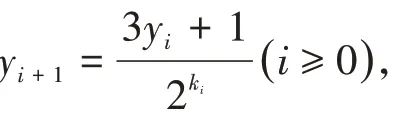
注意到关于y的一元方程3y+ 1 = 2ky（k为正整数）仅当k=2时有正整数解，此时唯一的正整数解y= 1.所以若{yn}n≥0是正奇数y0的3X+1迭代数列，则仅yi= 1时，才可能成立3yi+ 1 = 2kyi+1，此时k=2.若y0是不回归于1 的正奇数，则对任意非负整数i，yi>1，所以不回归于1 的正奇数的迭代数列不可能是最终常值数列，故下列推论成立.

推论3若y0是不回归于1的正奇数，{yn}n≥0是y0的3X+1迭代数列，则对任意非负整数N，{yn}n≥N既不是严格单调数列，也不是最终常值数列.

证明根据定义，3yi+ 1 = 2kiyi+1（i≥0），下用反证法证明，假设存在某个正整数n，使得yn≡0(mod3 )，则3yn−1+ 1 = 2kiyn，从而3yn−1+ 1 ≡2kiyn(mod3 )，进而1 ≡0(mod3 )，矛盾.所以假设不成立，命题得证.注：这个定理表明，在一个正奇数的3X+1迭代数列中仅首项可能被3整除.

定理3若y0是正奇数，{yn}n≥0是y0的3X+1迭代数列，则下列各条件等价：

（i）{yn}n≥1每项恒等于1;

(ii)y1=1;

（iii）为正整数}.

推论4对任意正整数k,是一个正奇数，且它是一个回归于1的数.

结束语：本文分别应用了初等数论的同余和组合数学中的求解递推关系两个工具来证明3X+1 迭代数列的若干性质.3X+1迭代数列还有不少性质值得我们去进一步探寻.若我们把推论4中给出的那些正奇数看成“第一层的回归于1 的数”，那么所谓的“第二层的回归于1 的数”又会有怎样的特征？“第n层的回归于1的数”又如何呢？这都是值得进一步探讨的问题.