带能力限制的混合形专用线非直达车流取送问题优化

李 冰, 徐光兰, 轩 华

(郑州大学 管理学院,河南 郑州 450001)

0 引言

铁路枢纽系统的货物流根据作业性质可分为中转流和地方流，而地方流的发送作业量往往占据较大比重。小运转作业系统是枢纽内本地货物运转的主要运输动力，通过在枢纽内开行小运转列车，将到达编组站的本地作业车送往公共货运站或工业站进行装卸货，同时将已完成装卸的货车取回至编组站。取送作业系统在枢纽货车集结和疏散过程中发挥着不可替代的作用，直接影响枢纽运送货物的时效性。

在货车取送作业优化方面，Jaehn等[1]研究了铁路专用线取送调车优化问题，构建了取送调车混合整数规划模型，并设计了多项式时间求解算法。Li等[2]用仿真方法研究了铁路树枝形专用线取送车问题。张文晰等[3]针对路企直通列车组织过程中车流整列到发的取送问题，研究了装卸区呈树枝形布置的取送车优化问题。牟峰等[4]以“先顺序、后批次”为构造取送车作业方案的总体思路，设计了取送车作业问题一般模型解的模块化构造方法。李冰等[5～7]针对铁路枢纽地方货物流的小运转作业系统，研究了树枝形铁路专用线非直达车流取送问题，并设计了启发式求解算法。Bettinelli等[8]研究了城市物流系统中带客户和中间设施时间窗要求的多程分离式货物取送问题，并提出了分支-切割-价格算法。Alyasiry等[9]研究了带时间窗和后进先出装载要求的货物取送问题，并构建了一个松弛网络流模型，并设计了一个精确求解算法。Zhang等[10]等研究了面向快时尚零售商的多品种货物同步取送问题，构建了问题模型，并提出了一种元启发式算法。Wang等[11]研究了以碳排量最小化为目标的合作绿色取送问题，提出基于合作博弈理论的精确求解策略。Danloup等[12]研究了带转运的货物取送问题，并设计了大规模邻域搜索算法和遗传算法对问题进行求解。Haddad等[13]研究了货物分批取送问题，并设计了一个局部搜索启发式算法。

目前针对铁路枢纽地方货物流的取送车问题研究主要集中在放射形和树枝形专用线网络，对混合形专用线取送车问题的研究开展较少。本文研究带能力限制的混合形专用线非直达车流取送问题(Taking-out and placing-in non-through wagons with capacity limited on hybrid siding，简称TPNTW&CL-HS)。组建基于货车在站停留车小时与调机取送成本之和最小化为目标的数学规划模型，并提出初始取送作业方案构造-取送作业方案更新-调机指派的三阶段综合优化策略(Three-stage integrated optimization procedure，简称TSIOP)。本文研究对完善服务铁路枢纽地方货物流的组织调度理论方法有重要意义。

1 问题建模

1.1 问题描述

TPNTW&CL-HS定义为混合形专用线网络中，多趟非直达列车陆续到达编组站，列车h中各本地作业车组hci需送往装卸站i并在装卸任务完成后取回编组站重新编组发车。考虑装卸站装卸能力、调机牵引能力、瓶颈区段能力、调机日走行时长等能力限制条件及其它可行性约束，以货车在站停留车小时与调机取送成本之和最小化为目标，合理安排各调机取送时机、顺序、批次方案。

1.2 符号变量

为构建模型，引入以下参量与变量：

1)集合

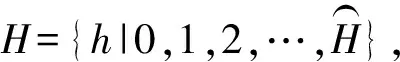
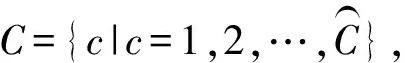
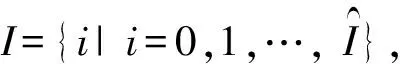
D：取送作业性质集合，记为D={d|d=1,2}，其中d=1表送车，d=2表取车。

R：取送车组集合，记为R={hci|h∈H,c∈C,i∈I}，表示随货物列车h到达并前往位于放射枝c中装卸站i作业的车组，其中0ci表示放射枝c中装卸站i的站存车组。

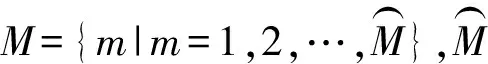
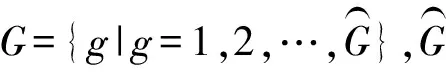
2)参数

O(hci)：车组hci的货车编组数，其中O(0ci)表示开始时车站内站存车编组数。

t1(hci)：车组hci挂运列车最晚编组时刻。

t2(hci)：车组hci装卸作业时间。

t(i,j)：装卸站i到装卸站j的走行时间。

Q：调机牵引能力。

T：调机日走行时长。

Oi：装卸站i的装卸能力。

F(i,j)：装卸站i到j瓶颈区段通过能力。

α1：调机的单位分钟运营成本。

α2：货车的单位分钟在站停留空费成本。

3)状态变量

t3(hci)：车组hci装卸作业完成时刻。

t4(hci)：车组hci取回后待编组时刻。

Zijg：第g批次取送作业中，调机途径装卸站(i,j)路段时所牵引的货车总编组数。

4)决策变量

1.3 模型构建

以在站停留车小时与调机取送成本之和最小为目标，考虑带能力限制的混合形专用线非直达车流取送中的实际约束，构建问题模型。

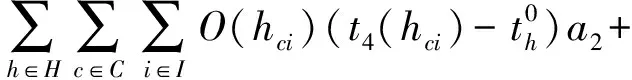
(1)

(11)

目标函数(1)表示货车在站停留车小时费用与调机取送成本之和最小；约束(2)要求同一车组先送后取；约束(3)要求在一个装卸站内同时作业的货车数量不能超过装卸站装卸能力；约束(4)要求相异放射枝上的取送作业所属批次不同；约束(5)要求任意路段牵引货车数不超过调机牵引定数限制；约束(6)要求对于路网中的特殊线路，携带货车数不超过线路通过能力限制；约束(7)要求车组取回编组站时间不超过所挂运列车最晚编组时间；约束(8)要求调机m负责的所有批次取送作业时间之和不超过调机日走行时长限制；约束(9)要求每批作业只能由一台调机来完成；约束(10)～(11)为变量取值约束。

2 三阶段综合优化策略

TPNTW&HCL-HS问题模型为典型的NP问题，利用传统算法很难求解且效率不高。故设计初始取送作业方案构造-取送作业方案更新-调机指派的三阶段综合优化策略。

2.1 基于TPA的初始取送作业方案构造

基于作业编码-顺序调整-批次划分的初始取送作业方案生成过程(Three phases approach for operation coding, sequence modification, and batch division，简称TPA)，具体步骤如下：

Stage1初始取送作业顺序集合。

Stage1.1取送作业编码集合。

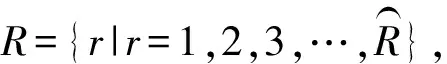
Stage1.2基于Randperm函数的取送作业顺序集合。对作业编码集合R利用Randperm函数生成n个初始取送作业顺序。

Stage2取送作业顺序调整。要求生成的初始取送作业顺序满足同一车组先送后取的偏序约束和装卸能力限制。若不满足约束，则对相应的作业执行局部调整，顺序互换。

Stage3取送作业批次划分。

Stage3.1基于相异放射枝的批次划分。将取送作业顺序中去往不同放射枝且相邻的两项作业划入不同取送作业批次。

Stage3.2基于牵引定数的批次划分,若批次g包含某项取送作业后超过调机牵引能力，将该项取送作业划为不同批次。

Stage3.3基于区段通过能力的批次划分,若批次g包含某项取送作业后超过区段通过能力。将该项取送作业划为不同批次。

Stage3.4基于取回时间窗的批次划分。假定某项取送作业为批次g的最后一项作业，计算批次g中带时间窗要求的车组取回站内的时刻，若不满足取回时间窗要求，则将该项作业划分为下一取送作业批次。

Stage3.5基于调机走行时长的批次划分。假定某项取送作业为批次g最后一项作业，判断第g批次是否满足走行时长要求，若不满足则将该项作业划分为下一批次。

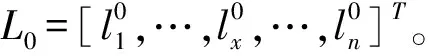
2.2 基于FPUA的取送作业方案更新

基于迭代寻优思路，设计四阶段更新过程(Four phases updating approach，简称FPUA)，具体步骤如下：

Stage1初始化设置

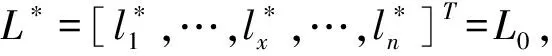
Stage2基于L*-L0交叉的取送方案一次更新

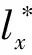
Stage3基于L′-lbest交叉的取送方案二次更新

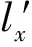
Stage4基于L″自变异的取送方案三次更新

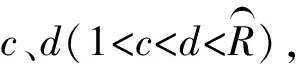
Stage5基于局部搜索的取送方案四次更新

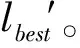
Stage6四阶段更新过程中L*和lbest的确定

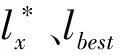
Stage7输出最优取送作业方案

输出第q次迭代得到的最新取送作业方案集合、状态传递集合L*和最优取送作业方案lbest。进而依次执行四次更新过程，直到迭代次数达到nMax为止，目标函数值最小的方案为最优取送作业方案。

2.3 基于批次时间窗-空闲原则-调机走行的调机配置

基于批次时间窗-空闲原则-调机走行的调机配置过程(engine assignment approach considering batch time, leisure principle, and engine workload，简称EAA)具体步骤如下：

Stage1基于发车时间的取送作业方案排列

Stage2基于批次时间窗的调机分派

对批次g=1分配编号为m=1的调机，再对批次g=2进行调机分派，此时判断调机m=1是否回到编组站，若没有回到编组站则启用调机m=2。

Stage3基于空闲原则的调机分派

对批次g分派调机时，优先选择先处于空闲状态的调机负责配送。如对g=4批次配送，假定此时编组站停留的调机为m=1，m=2，比较两台调机返回编组站时刻，并选择先返回的调机负责g=4批次配送。

Stage4基于走行时长的调机分派

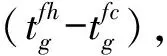
3 实验验证及结果分析

3.1 实验场景

1)混合形专用线网络

设计由3条放射枝，15个装卸站组成的混合形专用线网络，如图1所示。

混合形专用线网络中各装卸站及编组站间的调机走行时间数据如表1所示。

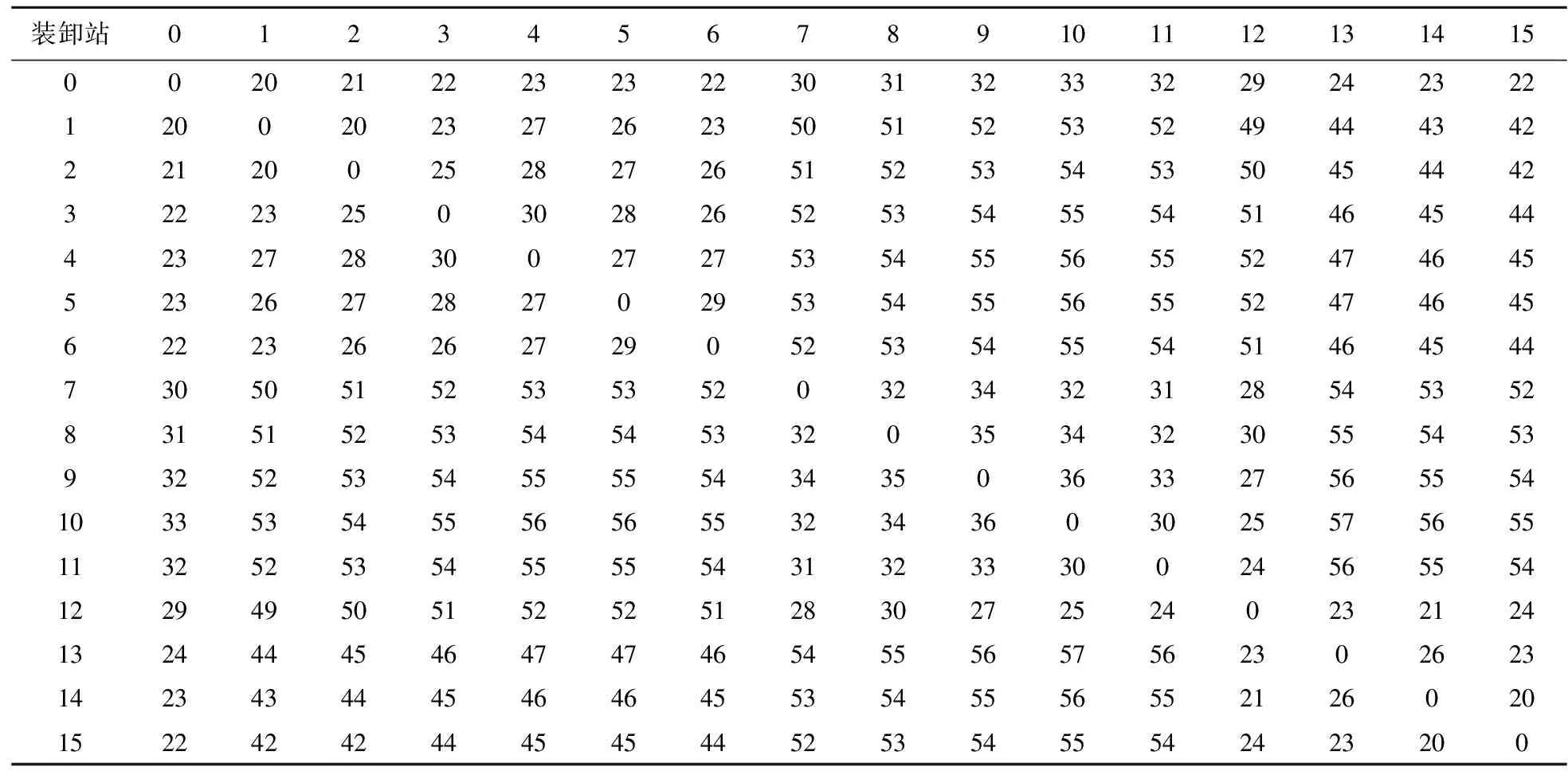
表1 装卸站间走行时间表(单位：min)

2)枢纽内本地作业车取送信息表

设计实验时段内有4列货物列车相继到达编组站，各列车解体后根据货车目的装卸站产生不同车组，包含列车及车组信息的车流及取回时间窗数据如表2所示。

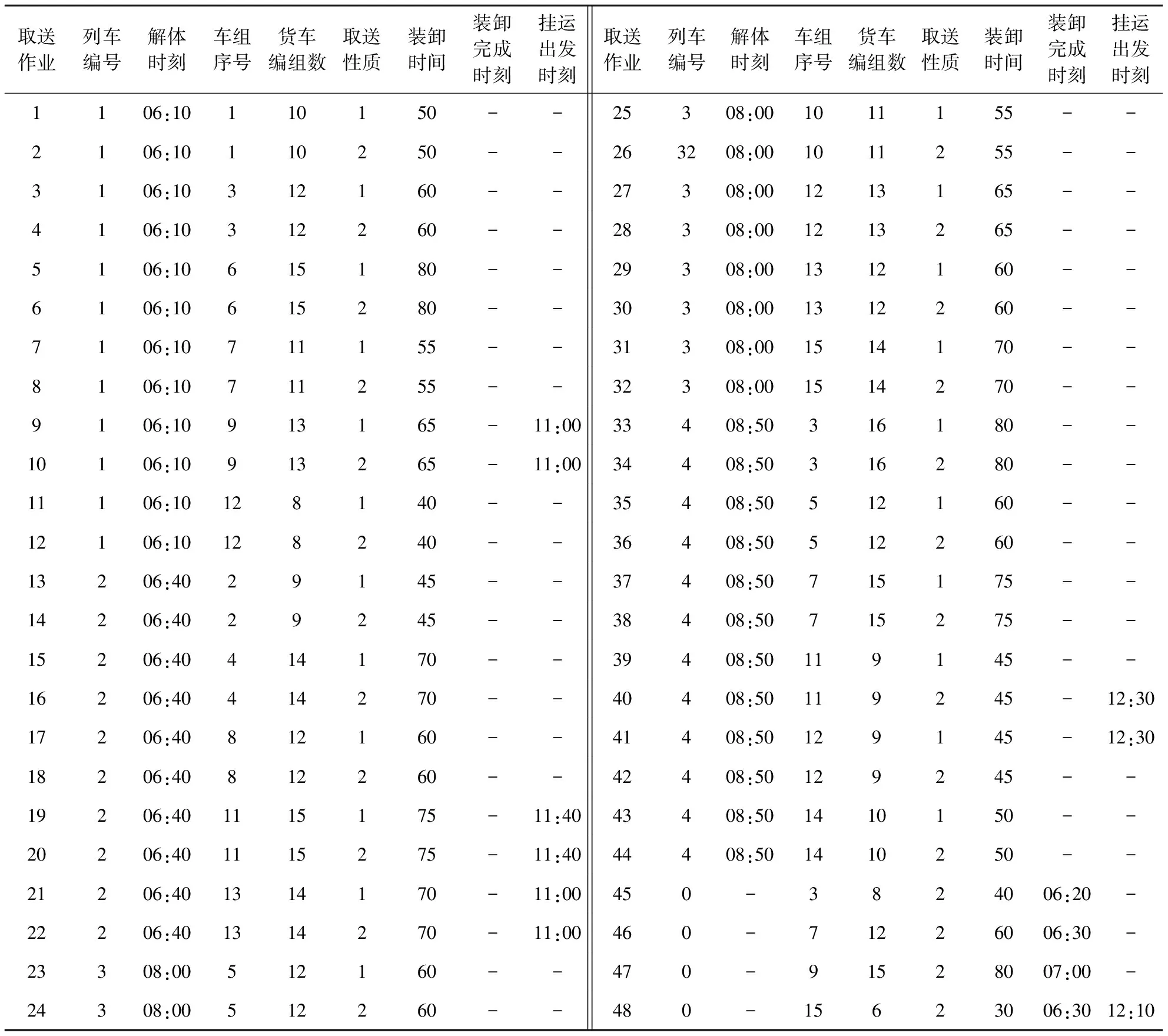
表2 枢纽内本地作业车取送信息表

3)装卸站装卸能力限制信息表

混合形专用线网络内的15个装卸站由于专用线有效长度有限，有最大装卸能力限制。各装卸站装卸能力信息如表3所示。

表3 装卸站装卸能力限制信息表

4)瓶颈区段通过能力限制信息表

混合形专用线网络内部分专用线区段上的车流通过量有限，设计当前路网中共有5条瓶颈区段有通过能力限制，如表4所示。

表4 瓶颈区段通过能力限制信息表

3.2 求解过程验证

在解决优化排序问题上，可以采取传统枚举法(enumeration method，简称EM)，也可以采取智能优化算法。智能优化算法中，标准遗传算法GA能够很好解决此类问题；标准粒子群算法PSO求解速度快、参数少、具有记忆性，在求解NP问题上具有较大的优势；改进粒子群算法wPSO对于粒子群算法中的惯性权重采取非线性权值递减策略，在粒子群算法基础上大幅提高收敛速度。为验证本文所提出TSIOP方法的高效性，引入EM传统算法和GA、PSO、wPSO等智能优化算法作为对比。

因GA、PSO、wPSO和EM法仅能优化取送作业顺序批次，无法进一步完成调机指派。故均需引入基于批次时间窗-空闲原则-调机走行的调机指派过程(EAA)来实现。从而四种对比算法简写为GA-EAA、PSO-EAA、wPSO-EAA和EM-EAA。为便于算法表述，四种比对算法分别简记为A1、A2、A3和A4。算法运行结果如表5所示。

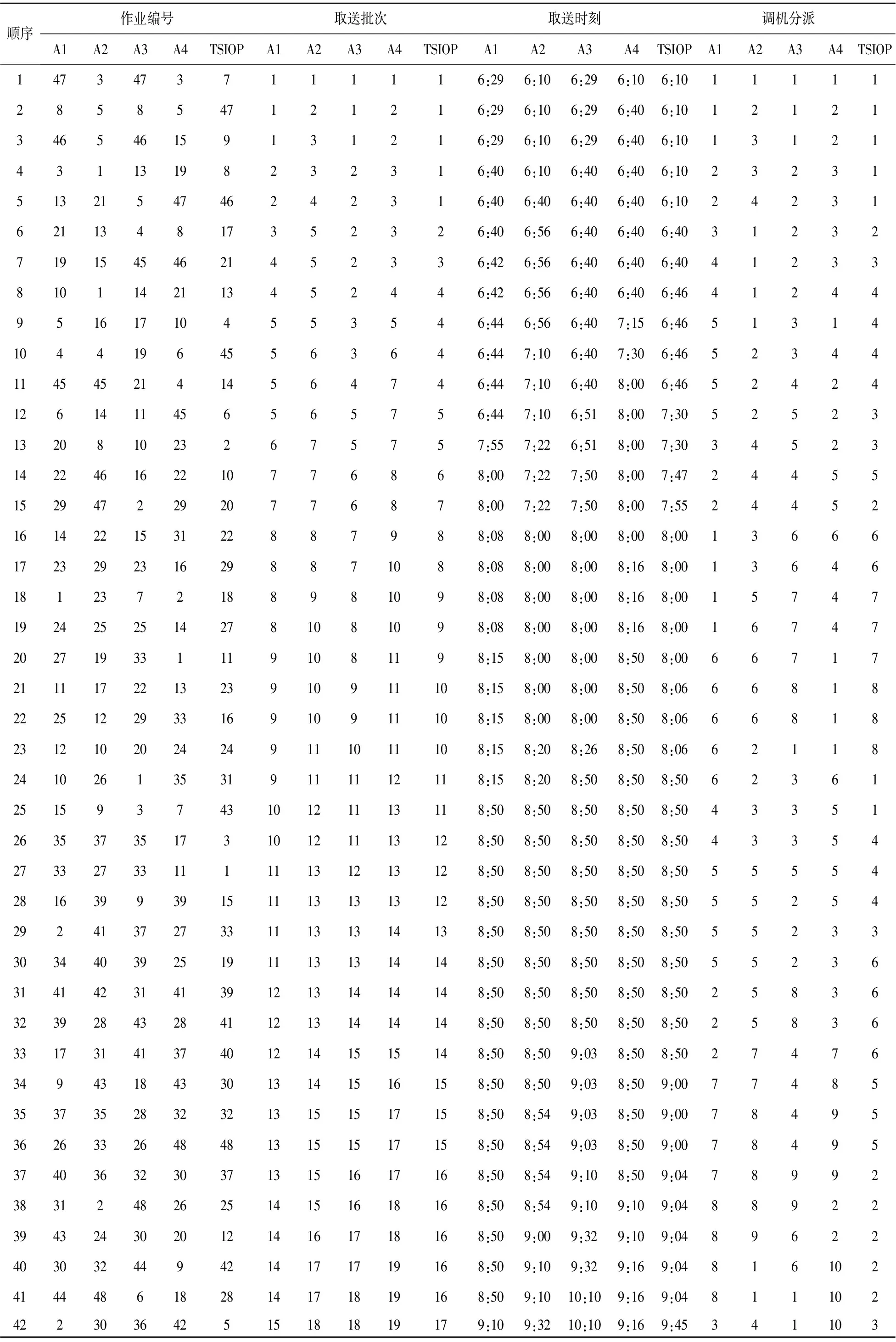
表5 五种算法的计算结果比对

3.3 算法性能评估

针对实验场景中给出的由3条放射枝、15个装卸站组成的混合形专用线网络，分别安排牵引定数为30辆和40辆的两种列车编组方案，算法种群规模分别安排在10和30，从而形成四组实验，对算法性能进行进一步评估。为避免运行结果的随机性，所有实验独立运行50次，设置智能优化算法最大迭代次数为400，传统EM-EAA枚举次数为智能优化算法种群规模×最大迭代次数。

取平均目标函数值、平均目标函数改进率和平均CPU运行时间作为算法性能的衡量标准，结果如表6所示。平均目标函数值用于衡量算法求解质量，值越小，算法质量越好。TSIOP对其他四种算法的平均目标函数改进率计算方法为：

β1=(GA-EAA-TSIOP)/TSIOP×100%

β2=(PSO-EAA-TSIOP)/TSIOP×100%

β3=(wPSO-EAA-SIOP)/TSIOP×100%

β4=(EM-EAA-SIOP)/TSIOP×100%

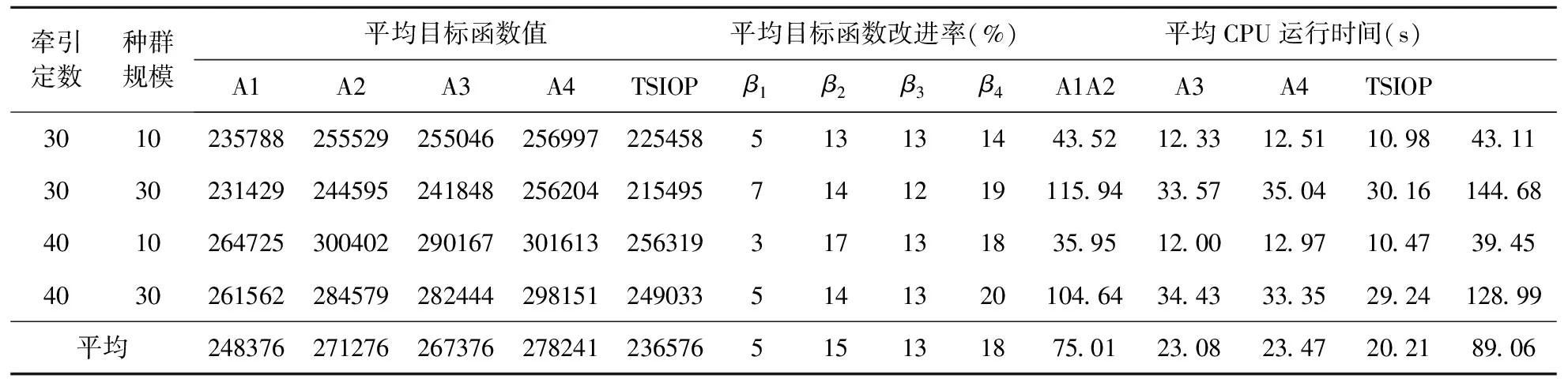
表6 五种算法在三放射枝混合形专用线网络中的性能测试比对

由表6数据可知，TSIOP的CPU耗时要高于其他四种对比算法，但在平均目标函数值与改进率上表现出明显的优势。

4 结论

本文研究了一类带能力限制的混合形专用线非直达车流取送优化问题。以在站停留车小时费用和调机取送成本之和最小化为目标，考虑装卸站装卸能力、调机牵引能力、瓶颈区段能力、调机日走行时长等能力限制条件，构建问题模型，并提出三阶段综合优化策略。该策略首先利用基于作业编码、顺序调整与批次划分的TPA过程完成初始取送作业方案生成，进而基于迭代寻优思路设计FPUA更新过程完成取送作业方案的优化，最后考虑批次时间窗、空闲原则、调机走行利用EAA过程完成调机分配。设计实验场景，对所提出的算法进行过程验证。本文研究没有考虑作业车在枢纽内不同装卸站间的调移问题。下一步研究工作将聚焦带调移的混合形专用线混合取送优化问题。