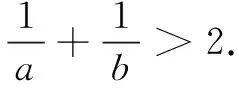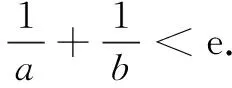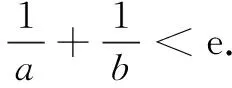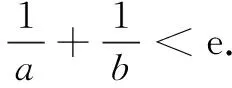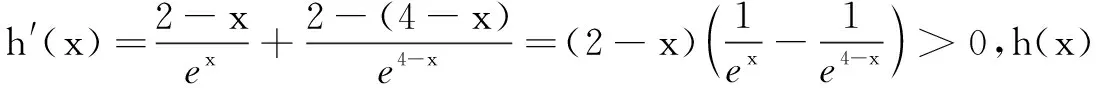一道导数压轴题的多视角探究
包军先
(山东省烟台第三中学,264000)
2021年新高考I卷第22题是一道导数压轴题,属于极值点偏移问题,主要考查运用导数研究函数的单调性,以导数为工具构造函数对不等式进行证明.考题的第(1)问是基础题,考生一般没有困难;第(2)问不等式证明是压轴题,对考生基本技能要求高,求解过程中转化难度较大、灵活性强.如果方法选择不当,答题时容易出现花费时间多、化简转化不到位、甚至无法完成解答.本文主要对第(2)问从不同视角给出几种常见的解法.
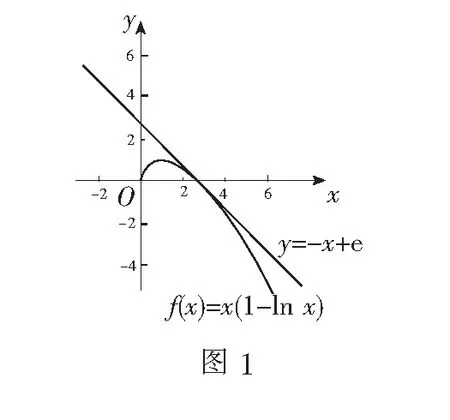
试题呈现已知函数f(x)=x(1-lnx).
(1)讨论f(x)的单调性;

解(1)函数f(x)在(0,1)单调增,在(1,+∞)单调减.(过程略)


当x>1时,令f(x)>0,可得1 先证x1+x2>2,即证x2>2-x1.由于2-x1>1,x2>1,且f(x)在(1,+∞)单调减,只需证明f(x2) 再证x1+x2 视角1构造差值函数证明 证法1要证x1+x2 所以x1∈(0,1)时,φ(x1)>0成立,即f(x1)>f(e-x1),亦即x1+x2 评注本解法的基本特点就是将待证不等式进行变形,使不等式两边变量落在同一个单调区间内,进而构造函数并通过函数值的大小关系比较出变量的大小关系. 视角2借助经典不等式放缩证明 证法2同证法1的分析,即证f(x1)>f(e-x1),其中x1∈(0,1). 于是φ(x)>x(1-lnx)-x=-xlnx>0. 评注本解法通过切线不等式ln(x+1)≤x对问题进行放缩简化的证明过程,解题效率较高. 视角3用放缩法化双变量为单变量 证法3由x1∈(0,1),x2∈(1,e),f(x1)=f(x2),可知x2(1-lnx2)=x1(1-lnx1)>x1.要证明x1+x2 令φ(x)=x(1-lnx)+x,x∈(1,e),则φ′(x)=-lnx+1>0,φ(x)在(1,e)单调增,可得φ(x)<φ(e)=e. 评注化双变量不等式为单变量不等式是证明双变量不等式的永恒主题,放缩法也是一种减少变量的有效途径. 视角4比值替换法减元构造函数 证法4要证明x1+x2 评注通过作比值(或作差)构造出新的主元建立函数关系,也是解决双变量不等式证明的重要方法. 视角5数形结合切线放缩法 证法5易求得曲线y=f(x)在x=e处的切线为y=-x+e.作f(x)=x(1-lnx)的图象及切线y=-x+e如图1. 设g(x)=f(x)-(-x+e)=2x-xlnx-e,则g′(x)=1-lnx,由此易见g(x) 在(0,e)单调增,在(e,+∞)单调减,从而有g(x)≤g(e)=0.所以f(x)≤-x+e恒成立. 由x2∈(1,e),可得f(x2)≤-x2+e.又f(x1)=f(x2),且x1∈(0,1),f(x1)=x1(1-lnx1)>x1,所以x1<-x2+e,即x1+x2 评注华罗庚教授曾说过“数形结合百般好,隔离分家万事休.”在不等式证明过程中,若能将问题用几何直观来描述,会给解决问题带来重要思路.这需要特别关注那些重要的切线放缩不等式. 总之,运用导数证明双变量不等式的基本思想是通过转化、换元、放缩等手段将二元不等式转化为一元不等式来证明. 纸上得来终觉浅,绝知此事要躬行!在此提供一道同类习题供读者练习使用. (1)求f(x)的单调区间与极值; (2)设m,n为两个不相等的正数,且满足mlnn-nlnm=m-n,证明:mn>e4. 参考解析(1)f(x)在(-∞,2)单调增,在(2,+∞)单调减;极大值f(2)=e-2,无极小值.(过程略) 不妨设x1=lnm,x2=lnn,x1 (2,+∞).要证mn>e4,只需证lnm+lnn>4,即x1+x2>4,即证x2>4-x1.因为4-x1∈(2,3),x2∈(2,+∞),且f(x)在(2,+∞)单调减,只需证f(x1)=f(x2) 综上,得证.