直观想象指引下函数多零点组合变量问题的解法探究

福建省南平市高级中学(353000) 江智如 应丽珍 蔡珺

1 问题提出

函数零点是函数的重要性质之一,是培养高中学生直观想象素养的有效载体,可以帮助学生结合已学的函数图象,了解函数零点与方程解的关系,理解函数零点存在定理[1],掌握运用函数性质解决实际问题的思想与方法.函数多零点组合变量问题是高考与各类模拟考的热点,难度大,综合性强,能够考查考生综合数学思想能力和数学素养,体现试卷的区分与选拔功能[2],需要学生借助几何直观和空间想象感知事物的形态与变化,建立形与数的联系,构建数学问题的直观模型,探索解决问题的思路[1],提升学生运用数学模型思想发现和提出问题、分析和解决问题的数学能力与素养.为此,本文在直观想象素养指引下,从不同的思维层次与能力水平出发,探究求解函数多零点组合变量问题的思路与方法[3].

2 概念界定

函数的零点是函数图象与x轴交点的横坐标[4],即关于x的方程f(x)=0 的实数解,要求学生能够结合已学函数图象,理解函数零点与方程解的关系[5].含参变量的函数本质上是一个多元函数,当我们研究其中某个自变量时,把其它变量看成参数,再根据参数的范围讨论研究相关的函数问题,是高中函数教学的重点和难点.因此,本文将函数多零点组合变量问题界定为:“以函数多零点为载体,结合含参函数的定义与性质,建构函数模型,求解函数取值范围的问题”.它能够培养高中学生函数与方程的思想、数形结合的思想、分类与整合的思想、化归与转化的思想,促进高中学生空间想象能力、运算求解能力、以及应用意识和创新意识的提升.

3 方法探究

函数多零点组合变量问题主要围绕函数的图象性质展开,利用初等函数的图象、零点存在定理、基本不等式等相关知识与性质,运用数形结合思想,运用函数与方程思想、建模思想,把多元问题转化为一元含参题型,通过灵活的推理论证能力和扎实的运算求解能力,最终解决问题.笔者在教学实践过程中,从高中学生的认知水平与数学能力出发,将此类问题归纳为四种解题方法:(1)消元去参法;(2)对称放缩法;(3)换元构造法;(4)化归函数法.

4 方法应用

(1)消元去参法 借助函数图象性质和相关知识确定参变量与零点的范围,消去参变量,把多零点问题转化为单个零点问题进行求解.应用的关键在于要熟悉掌握中学阶段所学初等函数的图象性质,会用函数的定义与性质读懂问题,分析问题,转化问题,解决问题[1];

题型1 (2021年福建南平期末第12题)已知函数f(x)=若方程f(x)=a有四个不同的解x1,x2,x3,x4,且x1< x2< x3< x4,则x3·(x1+x2)+的取值范围是( )

A.(−1,1] B.[−1,1] C.[−1,1) D.(−1,1)

评析本试题依托函数f(x)的图象,根据方法1,先确定参变量a的取值范围,再利用二次函数的对称性与对数函数图象的“翻折”性质,把所求式子消元为关于x3的函数,通过函数的单调性求得结果.考查考生对二次函数、对数函数知识的掌握程度,同时也考查考生函数与方程思想、化归与转化思想、数形结合思想.

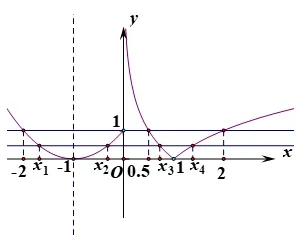
图1

(2)对称放缩法 从函数图象的对称性入手,把部分零点转化为常数或定值,减少零点个数,再根据零点的范围放缩运算得出结果.方法应用的关键在于消元转化,要求考生有扎实的数形结合思想与运算求解能力.

题型2 (2021年深圳市高三一模第8题)已知函数f(x)=若函数g(x)=f(x)−t,(t∈R)有3个不同的零点x1,x2,x3,则2x1+2x2+2x3的取值范围是( )

A.[16,32] B.[16,34) C.(18,32] D.(18,34)

思路如图2 作出函数f(x)的图象,由图可知,当0< t <1 时,函数g(x)=f(x)−t,(t∈R)有3个不同的零点.不妨设x1< x2< x3,则有1−2x1=2x2−1,即2x1+2x2=2,且4< x3<5,于是16<2x3<32,所以2x1+2x2+2x3∈(18,34),因此选D.

图2

评析掌握函数图象的对称性并能将其应用于零点范围的求解,是高中函数教学的重要内容之一.本试题是方法2 的典型应用,考生依据题设条件先作出分段函数的图象确定零点的范围,利用对称性,把多零点问题转化为关于x3的一元指数函数,运用单调性求得结果.所涉及的知识方法为考生所熟悉,易于入手,体现考生的数学能力和思维水平,有利于直观想象素养与数学运算素养的提升.

(3)换元构造法 对于复合函数的零点问题,常利用换元法,把问题转化为含参变量函数,再依据函数图象确定参变量的范围,进行分类讨论,并结合初等函数的性质、零点存在定理等知识最终解决问题.应用的关键在于换元构造并对参数分类讨论,考查考生化归与转化思想、分类与整合思想.

题型3 (2021年哈尔滨三中期末理科第12题)已知函数f(x)=若函数F(x)=f2(x)−2af(x)+的零点个数为4,则实数a的取值范围为( )

图3

思路令t=f(x),则F(x)=t2−2at+,从而函数F(x)有4个不同零点转化为函数g(t)=t2−2at+有两个不同的零点.设零点分别为t1,t2,不妨设t1< t2,其中t1·t2=,那么关于x的方程f(x)=t1和f(x)=t2分别有两个不同的解.作函数f(x)的图象3,由t=f(x)有两个不同解及t1·t2=,可得0< t1≤1 及t2>2,.如图4,由二次函数图象及零点存在定理得

图4

解得a>,因此选D.

评析本试题以复合函数的零点问题为载体,考查二次方程根的分布问题,来源于教材,又高于教材.试题考查内容重点突出,不但体现《课程标准》[1]的基本理念,而且体现对知识的考查侧重于理解和应用的要求.通过巧妙的换元,化繁为简,以使考生能运用所学知识加以解决,考查考生的数学核心素养、数学建模的思想以及综合运用所知识解决实际问题的能力.

(4)化归函数法 对于求解参变量与多零点混合模式的问题,常根据函数的图形性质,把多零点转化为关于参变量的表达式,构造函数,利用函数知识求解问题.应用的难度在于化简多零点与构造关于参变量的函数,考查考生数形结合思想和化归转化思想.

题型4 (2021年天津南开区4月质检第9题)已知函数f(x)=若函数g(x)=a−|f(x)|有四个零点x1,x2,x3,x4,且x1< x2< x3< x4,则的取值范围是( )

A.(−1,+∞) B.[4,+∞) C.[1,4) D.[1,2)

图5

思路问题可等价于方程|f(x)|=a有四个零点,于是作出函数|f(x)|的图象5,得到a∈(0,2],再由图象的对称性求得x1·x2=1,从而可得ax1x2+=a+.令h(a)=a+,a∈(0,2],则由均值不等式求得a+≥4,当且仅当a=2时等号成立,因此选B.

评析本试题围绕分段函数的对称性,把多零点转化为定值,从而把问题化归为关于参变量的一元函数,再结合图象确定参变量的范围,运用均值不等式求出结果.试题融入多个知识点,为考生综合应用所学数学知识创造条件,既在基础性、综合性、应用性与创新性等方面考查考生,又在直观想象与逻辑推理等数学核心素养方面考查考生,体现试题的区分度与选拔功能.

5 综合应用

以上四种解题方法,虽然解答的问题与方法不同,但殊途同归,可归纳为“一画二消三化四构造”,即画出函数的图象,消参或化归,构造函数,转化为一元函数进行求解.考生可以灵活运用已学函数的知识和图象性质,依托“精致练习”[6]的解题训练,提高化归与转化思想的意识水平,有效实现函数多零点问题与函数知识的相互转化[7],最终解决问题.

题型5 (2017年江西上饶一模第16题)已知函数f(x)=.若函数F(x)=f(x)−3 的所有零点依次记为x1,x2,x3,···,xn,且x1

评析本试题给出正弦函数在定区间上的零点个数,考查正弦函数的周期与对称性质.考生在研究此类问题,一般从三角函数的周期入手,利用三角函数图象的直观性,在整体上建立数与形的关联,再根据周期与对称性质确定零点的取值范围,最终解决问题,全面考查考生对正弦函数知识的理解与掌握情况,丰富考生解决问题的思维方法,为考生提供发挥的空间.

题型6 (2022年金太阳1月联考第11题)已知函数f(x)=若方程f(x)=k有四个不同的解x1,x2,x3,x4,且x1< x2< x3< x4,则下列结论正确的是( )

A.0

C.2x1+x2>3 D.x1+2x2的最小值为

思路作函数f(x)的图象6,可知0< k <1,故A正确;当x≤2 时,由f(x)=|log2x|的性质得,x1x2=1,当x >2 时,由二次函数的对称性得x3+x4=8,于是x1x2(x3+x4)=8 为定值,故B 正确; 因为x1x2=1,所以1< x2<2,于是,当且仅当时等号成立,故C 错误;同理,当且仅当时等号成立,与1,故D 错误,因此选AB.

图6

评析本试题是以多零点问题为背景的多选题,其本质是考查零点的取值范围.涉及函数的对称性、单调性、均值不等式求最值等基本性质.要求考生理解掌握函数性质与图象之间的联系,综合性强,可以较好地区分不同层次的考生,具有较好的选拔功能.同时试题的设计关注了新课程标准下函数性质与图象的教学要求,有利于考查考生逻辑分析能力、构图想象素养及运算求解能力.

6 结语

前苏联女数学家C.A.雅诺夫斯卡娅指出:“解题就是把题归结为已解过的题”[8],所以函数多零点组合变量问题解决的一个基本特征就是“多步化归”,通过多步化归,把一个未知的问题转换为一个已经解决的问题.因此,在日常的教学实践中,教师可以在适当的时机对过程方法实时总结或迁移,依托函数图象,由形到数,以数释形,数形结合贯穿其中并逐层递进,帮助学生在交流和反思中领悟数学思想方法在数学学习中的指导作用[9],夯实数学基础,提升数学综合素养.