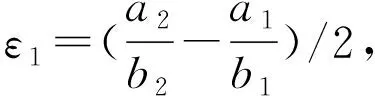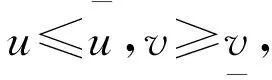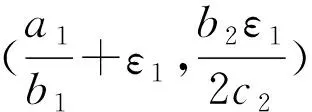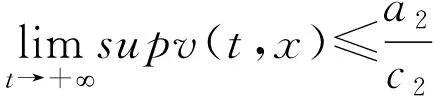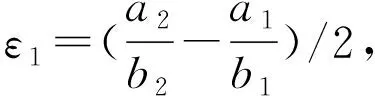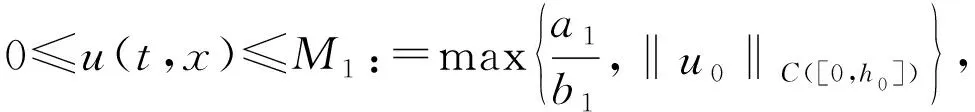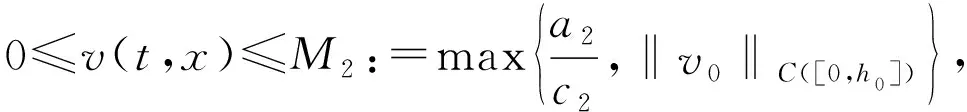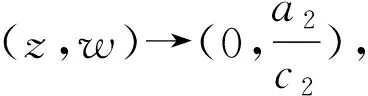一类竞争模型解的长时间渐近行为
张顺芹,朱雪格,刘晓薇
齐鲁工业大学(山东省科学院)数学与统计学院,山东 济南 250301
近年来,外来物种入侵逐渐成为人们热议的话题,同样也引起了许多数学家的关注,为此他们建立了竞争模型[1]从生物数学的角度进行了研究。随着研究的深入,发现在有界的特定区域上建立的竞争模型具有一定的理论缺陷,因此数学家们引入了自由边界来避开这些缺陷,自由边界的生态背景可参考[2]。
目前带自由边界条件的竞争模型已经有了广泛的研究。例如,王明新和赵景服[3-4]考虑了带Dirichlet和Neumann边界条件的一维空间反应扩散竞争模型,证明了在强-弱、弱-强两种情形下入侵物种扩张和消失二择一性质成立,并且给出了物种扩张时自由边界渐近扩张速度的一个估计。郭忠勝等[5]研究了带Neumann边界条件的强-弱情形,证明了两个物种扩张时,存在一个临界值,使得当其领地范围大小高于该值时,优势竞争物种总是能够成功扩张。杜一宏等[6]提出了具有Neumann边界条件的高维空间反应扩散竞争模型来描述入侵物种的传播,讨论了强-弱、弱-强两种情形,并给出了u发生扩张时扩张速度的一个粗略估计。
上述研究都是针对于Dirichlet和Neumann边界条件,而关于Robin 边界条件的研究却极少,因为带Robin边界的竞争模型更符合某些实际情况中的物种传播过程,具有理论意义和实际意义[7-9],所以本文我们主要考虑以下带Robin自由边界的Lotka-Volterra模型:
其中x=h(t)是待确定的移动边界,h0,μ,di,ai,bi,ci(i=1,2)是给定的正常数,初始函数u0,v0满足
本文主要讨论了u是劣势竞争者的情形,即
1 初步结果
类似参考文献[6]的方法,我们得到(H1)解的全局存在性,即:
引理1.1对于满足(H2)的(u0,v0)和任意的α∈(0,1),存在一个T>0,L>0使得当u(a1-b1u-c1v)≤L(u+v),v(a2-b2u-c2v)≤L(u+v)时,对任意t>0,问题(H1)有唯一有界解:
(u,v,h)∈C(1+α)/2,1+α(DT)×C(1+α)/2,1+α(DT)×C1+α/2([0,T]);
且‖u‖C(1+α)/2,1+α(DT)+‖v‖C(1+α)/2,1+α(DT)+‖h‖C1+α/2([0,T])≤C,
其中DT:={(t,x)∈R2:t∈[0,T],x∈[0,h(t)]},C和T只取决于h0,α,‖u0‖C2([0,h0])和‖v0‖C2([0,h0])。

令(u,v,h)是(H1)的唯一有界解,则
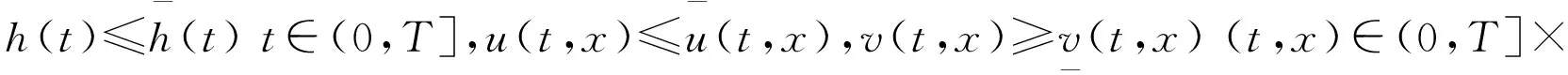

利用引理1.2,易知下列定理成立。
引理1.3 问题(H1)有唯一的一致有界解(u,v,h),即在t>0上都有解,存在常数M1和M2使得
0 0 并且存在一个常数M3使得 0 而且(H1)没有任何无界解。 证明:当t>0,x∈[0,h(t)]时,由比较原理得u(t,x)≤u*(t),其中 是问题 的解 令v*是下列问题 现在(u,v)满足 证明:首先根据比较原则 当t>0,0≤x<∞时,有v(t,x)≥δe(-b2M1-c2M2)t。 然后考虑下列问题: 根据比较原理u(t,x)≤z(t),v(t,x)≥w(t),t≥t1,0≤x≤∞。在假设条件 直接计算可得 在[T*,t]上积分得 因为(a1-b1u(t,x)-c1v(t,x))≤0,t≥T*,0≤x<∞,我们有 则h∞<∞。 定理2.2表明劣势竞争者不可能深入到一个建立良好的本地物种栖息地,它在入侵的锋线到达一定的有限限制位置之前就灭绝了。 定理2.3 如果(H3)成立,则对于所有的μ>0有h∞<∞。2 解的长时间渐近行为