基于小波分形插值算法的大气湍流波前畸变重构
马圣杰, 王 勇, 郝士琦, 赵青松, 徐晨露, 魏 硕
(1.国防科技大学脉冲功率激光技术国家重点实验室,合肥,230037;2.国防科技大学电子对抗学院,合肥,230037;3.电子制约技术安徽省重点实验室,合肥,230037;4.32032部队,北京,1000094;5.92118部队北极星船,浙江舟山,316000)
1992年Allen等人首次发现涡旋光携带轨道角动量(orbital angular momentum,OAM)[1],且携带不同模式OAM的涡旋光之间相互正交,并形成一个一维无限大的希尔伯特空间,能够传输无限大比特的信息,可以有效地扩大通信系统的信道容量[2-4]。然而涡旋光在大气中传输时不可避免会受到大气湍流的影响,使得涡旋光波前发生畸变,导致接收端误码率增加,影响通信系统的性能[5]。为了确保通信的可靠性,可以对畸变的波前进行校正。
自适应光学(adaptive optics,AO)技术利用相位共轭原理或优化算法补偿波前畸变进而对畸变进行校正[6]。根据系统结构的不同,可以分为有、无波前传感器的AO系统[7]。有波前传感器的AO系统对接收到的光束进行波前探测,获得斜率信息,然后对波前进行重构,最后由波前校正器对畸变进行校正,因此波前重构的精度在很大程度上决定了校正效果。现有的波前重构算法有直接斜率法、模式法和区域法[8]。直接斜率法将波前传感器探测到的信息与变形镜的响应特性建立关系,通过拟合算法直接计算出控制电压信号;模式法的基本原理是将波前展开成不同模式的加权叠加,然后通过探测器对波前斜率进行探测并计算出不同模式的加权系数,最后进行加权叠加,进而把波前相位信息重构出来;区域法则是直接基于各个子孔径测得的波前斜率计算波前相位。
上述波前重构方法得到的重构波前精度不是很高,影响了校正效果,为了取得更好的校正效果,需要提高重构波前的精度。分形插值技术的一个基本特征就是能够展示事物的精细结构,通过提取图像的分形参数,可以实现在任意分辨率下生成逼近图像,提高图像的精度[9]。然而分形插值技术由于其平滑效应不可避免会造成高频信息的损失,进而导致重构波前的误差变大,为了解决这一问题,本文提出一种基于小波分形插值的波前畸变重构方法。
1 波前畸变自相似性分析
1986年Darnsley提出分形插值算法,该算法克服了传统插值算法(如双线插值、样条插值等)引起的平滑效应,能够有效提高图像的分辨率和精度,目前该方法已经广泛用于图像处理等领域。为了验证该方法可以用来提高大气湍流引起的波前畸变重构的精度,本文首先对波前畸变进行自相似性分析。
A. P. Pentland等人研究表明自然界中大多数图形服从分形布朗随机(fractal Brownian random, FBR)模型[12],FBR模型可以表示为:
E|BH(x+Δx)-BH(x)|2=E|BH(x+1)-
BH(x)|2|Δx|2H
(1)
式中:E|·|表示期望值函数,|·|表示取模运算符;BH(x)表示图像上任意一点的像素值,x为像素点位置,Δx表示两个像素点之间的距离;H为Hurst指数,用来描述分形图像表面的粗糙程度。令σ2=E|BH(x+1)-BH(x)|2,则可将式(1)化简为:
logE|BH(x+Δx)-BH(x)|2-2Hlog|Δx|=logσ2
(2)
通常采用相位结构函数(phase structure function, PSF)描述大气湍流信道中波前畸变的空间统计特性,其定义为:
Dφ(r)=E[φ(ρ+r)-φ(ρ)]2
(3)
式中:ρ和r分别表示接收端波束表面的二维矢量。大气湍流Kolmogorov功率谱对应的PSF表示为:
Dφ(r)=6.88(|r|/r0)5/3
(4)
式中:r0表示大气湍流的相干长度。结合式(2)和(3),大气湍流的PSF函数可写为:
logE|φ(ρ+r)-φ(ρ)|2-2Hφlog|r|=logσφ2
(5)
式中:Hφ=5/6,σφ2=6.88r0-5/3。式(5)与式(2)具有相同的表达形式,表明大气湍流导致的波前畸变分布服从FBR模型,因此,采用分形插值方法提高重构波前畸变的精度具有理论上的可行性。
2 小波分形插值原理
分形插值的实质是一种递归中点的位移过程,其基本原理为[10]:
1)当像素点的坐标位置(x,y)均为奇数时,分形插值后的大小不变;
2)当像素点的坐标位置(x,y)均为偶数时,分形插值后的大小变为:
BH(x+1,y+1)+BH(x-1,y+1)]+
(6)
3)当像素点的坐标位置(x,y)为一奇一偶时,分形插值后的大小变为:
BH(x+1,y)+BH(x,y+1)]+
(7)
式中:gφ为高斯随机数,且有gφ~N(0,σφ);Δr为像素间距。
分形插值技术虽然能够有效提高图像的精度,但对图像的处理并没有涉及频域信息处理,且存在高频信息丢失的问题,本文结合小波变换和分形插值技术对畸变的波前进行重构。
小波变换具有多分辨率分解的能力,在图像分解过程中利用滤波器和高通滤波器能够将图像包含的信息一层一层分解出来。M×N大小的图像f(x,y)进行离散小波变换(discrete wavelet transform,DWT)公式为[11]:
(8)
式中:f(x,y)为原始图像;j0为小波变换尺度;Wφ(j0,m,n)为尺度j0处的近似系数;φj0,m,n(x,y)为尺度函数。
二维离散小波变换过程见图1上半部分。首先对图像的每一行进行一维DWT,得到水平方向上的低频分量L和高频分量H,然后对变换后图像的每一列进行一维DWT,得到4组分量,即低频分量LL1,以及水平方向、垂直方向和对角方向的3组高频分量LH1、HL1、HH1。二维DWT就是在一维DWT的基础上对低频分量LL1重复上述步骤,得到LL2、LH2、HL2、HH2这4个新的分量。

图1 二维离散小波变换过程及小波分形插值原理图

3 仿真结果及分析


图2 原始波前

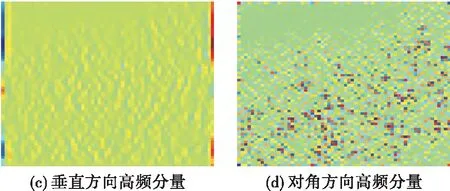
图3 小波变换后的分量
图4为经过小波分形插值后的低频分量和高频分量。对比图3(a)和图4(a)可以发现,主观上看,低频分量经过小波分形插值后图像的分辨率有所提高,纹理信息和细节也更加精确。以对角方向的高频分量为例,图3(d)中高频分量的纹理信息较模糊,且左上角还存在部分信息的丢失,图4(d)中分形插值后的对角分量包含更多的纹理信息,左上角的信息有所增强,且插值后图像具有更高的分辨率,包含更多的细节信息。根据上述分析,图像经过小波分形插值后,其精度都有一定程度的提升,对高频分量的提升较为明显。
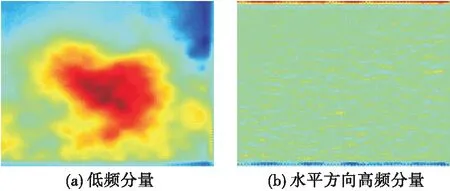

图4 分形插值后的分量
图5为使用传统的最小方差估计(minimum variance estimation, MVE)算法[12]得到的重构波前,图6为选取SymletsA小波系作为小波基,经过小波分形插值后得到的重构波前,对比MVE方法重构得到的波前,本文提到的利用小波分形插值重构得到的波前分辨率和精度有明显的提高,纹理信息和细节也更丰富,能够更好地还原原始波前的信息。

图5 基于MVE算法的重构波前

图6 基于小波分形插值算法的重构波前
本文选取灰度平均梯度[13](gray mean grads,GMG)以及均方根误差(root mean square,RMS)衡量波前重构效果,通常情况下GMG越大重构图像效果越好,RMS越小重构误差越小。
(9)
(10)
式中:M、N为图像f(x,y)的尺寸;fd(x,y)、fr(x,y)分别为畸变波前和重构波前。为减小随机性的影响,本文取多次实验的平均值,使用MVE方法得到的重构波前的GMG为0.065,经过小波分形插值后GMG增大到0.378 1,同时重构波前与原始波前的RMS也由3.249 2减小到0.635 1。数值计算结果表明使用小波分形插值算法得到的重构波前不仅提高了重构精度也减小了重构过程中的误差。
有波前传感器的自适应光学系统的校正性能除了与波前重构精度有关外,还与波前重构速度有关,波前重构速度越快,校正实时性越好。MVE算法重构波前耗时为1.142 s,而小波分形插值算法重构波前耗时为1.115 s,波前重构速度提高2.3%,进一步优化了系统的校正性能。
上述结果是选取SymletsA小波系作为小波基得到的,为了进一步比较不同小波系在小波分形插值中的性能,选择了其余的几个经典小波函数[13]进行小波分形插值处理,并计算出对应的GMG和RMS数值,具体结果如表1所示。

表1 重构波前与原始波前的均方根误差
整体上看小波分形插值重构得到重构波前的RMS基本上都小于MVE方法,GMG都大于MVE方法,数值结果表明基于小波分形插值算法的重构波前在提高精度的同时也进一步减小了误差。
另外采用不同的小波基时波前重构的效果也不一样,从重构效果来看,使用Haar小波系时波前效果最差,其次是Biorthogonal、SymletsA、Coiflet,使用Daubechies小波基时重构效果最好;从重构误差角度来看,采用Haar系列小波基时效果最好,其次是Biorthogonal、SymletsA、Coiflet,使用Daubechies小波基时效果最差。Daubechies(dbN)小波系是小波分析学者Inrid Daubechies构造的,除了db1即Haar小波外,其他的小波都没有明确的表达式,且小波不具有对称性,即在对信号进行分析和重构时会产生一定的相位失真,因此选取Daubechies作为小波基对波前进行重构时RSM较大。Coiflet小波系是Inrid Daubechies根据R.Coifman的要求构造的,具有coifN(N=1,2,3,4,5)这一系列的小波,Coiflet小波系波形接近对称,因此选取Coiflet小波系作为小波基时,重构波前与原始波前的RSM小于Daubechies小波系。当使用同一个小波函数进行分解和重构时,不能同时满足对称性和重构精度的要求,而采用两个函数则能较好地解决上述问题,Biorthogonal小波系在对波前进行重构时为了解决对称性和精确信号重构的不相容问题,引入了双正交小波,即采用一个函数对原始波前进行小波分解,然后采用另一个小波函数对波前进行重构,Biorthogonal小波函数通常可以表示为biorNr.Nd的形式,本文仿真采用bior4.4。Symlets小波系是Inrid Daubechies在Daubechies小波系的基础上进行改进得来的,通常表示为symN(N=2,3,…,8),与Daubechies小波系相比,Symlets小波系在连续性、支撑长度、滤波器长度等方面与Daubechies小波系一致,但Symlets小波系具有更好的对称性,一定程度上能够减少对信号进行分析和重构时的相位失真。
上述分析验证了使用小波分形插值方法对波前重构的可行性,且与传统的MVE方法相比,使用小波分形插值重构的波前不仅具有较高的分辨率,能够更好地重构出原始波前的纹理信息和细节部分,而且重构的波前与原始波前的RMS也比MVE方法小,可以确保取得更好的校正效果。
4 结语
涡旋光在大气中传输时不可避免会受到大气湍流的影响,导致波前发生畸变,影响通信系统的通信性能,因此需要对畸变进行校正。有波前传感器的自适应光学系统通过波前传感器对波前进行探测从而重构波前,最后由波前校正器对畸变进行校正。然而现有的重构算法重构波前的精度较低,影响校正效果。为提高重构波前的精度,优化校正效果,本文提出一种基于小波分形插值算法的波前畸变重构。与传统的MVE算法相比,本文方法明显提高了波前重构的精度,GMG由0.065提高到0.765 4,且RMS也由MVE算法的3.249 2减小到了0.426 9,在提高精度的同时也进一步减小了波前重构的误差。该方法对于提高重构波前精度,优化自适应光学系统校正性能有一定意义。

