基于Kriging算法的电磁频谱地图构建技术研究
胡炜林, 刘 辉, 彭 闯, 王伦文
(国防科技大学电子对抗学院, 合肥, 230031)
现代战争中,电磁环境异常复杂,掌握“制电磁权”是作战的关键[1]。因此,构造准确的电磁频谱地图、获取战场电磁能量分布、实现电磁环境可视化,可以间接反映战场电磁态势的变化,为电磁态势等级评估和威胁判断提供参考,其意义不言而喻[2-4]。
电磁频谱地图(spectrum map)也被称为无线电环境地图、电磁环境地图[5-6]。为了构建精确的电磁态势,众多研究者从电磁频谱地图入手,开展了广泛的研究。夏海洋等人[7]将电磁频谱地图的构建方法分为空间插值构建法、参数构建法和混合构建法,仔细比较了各个算法之间的优劣。Marek Suchansk等人[8]在多场景下比较了Kriging、IDW和NN等8种算法的无线电环境地图的构建精度,得出Kriging算法较为精确的结论。张舒明等人[9-10]采用改进模基参数估计法重构电磁场,使得在采样较低的情况下也能取得较好的效果,但由于结合了滑动窗口模型,算法计算量较大。蒋涵铭[11]基于残差改进和滞后距改进的Kriging插值算法提升了原有算法预测结能,但是采集点较多,不适用于战场紧张的装备数量。路镜涵等人[12-13]针对辐射源过多时重构性能不理想的问题,提出基于观测值插值的频谱地图重构方法,利用电波传播模型改进Kriging算法,但算法须知的辐射源参数等先验信息难以获得。随着人工智能的兴起,众多的神经网络算法也应用到电磁态势的构建中来,韩旭等人[14]结合认知无线电,利用深度神经网络复原残缺的功率频谱图。此外,周宇等人[15-16]将支持向量机替换变异函数,采用改进克里金算法生成电磁态势,算法精度高于其他经典算法。但是神经网络系统由于训练时间较长、训练数据庞大、实际可训练数据不足,因此实时效果有待提高。
现代战场上由于地形等因素限制,感知节点数量有限、部署位置随机性大,影响了电磁频谱地图构建效率,因此本文提出一种基于改进的Kriging算法的电磁频谱地图构建技术。
1 基于Kriging算法的多粒度电磁频谱地图构建原理
鉴于直接采用Kriging算法构建效率不高,结合K-means聚类算法实现多粒度划分,形成层次不同的多个局部区域,在这些区域基于Kriging算法构建多个电磁频谱地图,再依据感知节点分布状况,采用Voronoi图计算不同粒度下局部区域的均匀度权重,对各电磁频谱地图进行加权融合,进而构建电磁频谱地图。
1.1 电磁频谱地图生成简介
电磁频谱地图生成流程如图1所示,其中左图表示感知区域的地形和节点分布,曲线是等高线,颜色代表海拔高度,采用伪彩色图映射曲线颜色,蓝色系表示低海拔,红色系表示高海拔,其中黑色实心圆代表感知节点,通过感知节点测量电场强度值(electric field strength,EFS),从而得到中间所示图的节点感知数据,数值大小同样采用伪彩色表示。在此基础上,进行插值估计和数据融合,生成右图所示的电磁频谱地图,场强大小以伪彩色图表示,蓝色系表示低场强,红色系表示高场强。
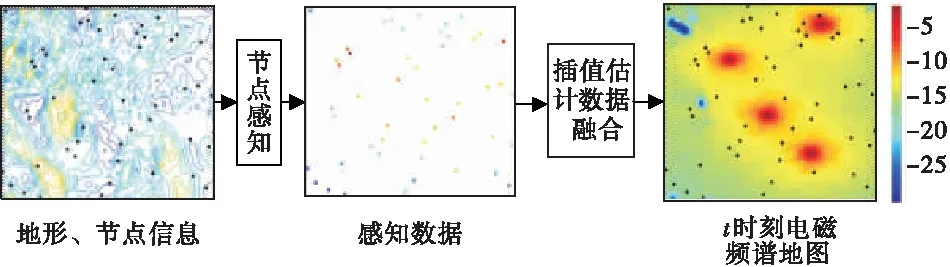
图1 电磁频谱地图处理流程
由于感知节点因为地形等因素分布不均匀,影响了电磁频谱地图构建效率,因此本文考虑在Kriging插值估计的基础上,提出多粒度的插值方法,提高电磁频谱地图的构建精度和效率。
1.2 Kriging插值法基本原理
Kriging插值法是一种空间插值法,又被称为空间自协方差最佳插值法,是传统地统计学的主要内容之一[17]。它以变异函数理论和结构分析为基础,通过邻域范围内的已知节点属性,对未知点进行线性无偏估计[18]。通过已知感知节点测量的电场强度值(EFS)来估计未知点的EFS,达到构建电磁频谱地图的目的。
(1)
式中:λi是未知点邻域内第i个感知节点的电场强度E(si)的权重。
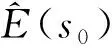
(2)
变异函数是Kriging插值算法的核心部分,通过变异函数能够利用感知节点的EFS值随两点距离得到变化关系,推断出未知点的EFS值。常见变异函数模型有线性模型、高斯模型、球形模型等。拟合变异函数时,采用最小二乘法代入现有变异函数模型进行拟合,求得模型参数。将变异函数模型代入式(2)并化简求得权重λi和拉格朗日乘子μ,即:
(3)
1.3 粒度划分与均匀度评估
由于感知节点分布不均匀,为了提升电磁频谱地图的构建精度,对评估区域进行多粒度划分,构造局部均匀的感知节点布局。粒度表示电磁频谱地图的构建区域大小,粒度划分是指将作战区域从粗粒度到细粒度地划分为不同粒度的局部区域,对不同粒度下局部区域分别进行Kriging插值,提高局部区域的电磁频谱地图精度。
根据感知节点的位置分布,进行K-means聚类实现粒度划分。首先假设将n个已知节点(xi,yi),i=1,2,…,n,随机分为k类,随机初始k个聚类中心;其次根据式(4)计算聚类中心以外的每个点与聚类中心的欧式距离,将点赋给最近的中心点构成k个聚类簇;然后重新计算每个聚类簇的平均值,再次确定新的聚类中心,根据式(5),直到每一聚类簇的平方和最小[19]。
(4)
(5)
式中:O是所有的聚类簇;μi是Oi中所有点的均值。
由聚类肘部法则可知,每个类别距离其该类中心点的距离称为畸变程度,其核心指标为误差平方和SSE,见式(5)。最后根据该法则,确定最佳聚类数量K值,实现感知节点的最佳粒度划分。
根据Kriging插值算法的推导,变异函数的自变量分布越均匀、密集,拟合曲线越精确,则估计值误差越小[20]。为了衡量感知节点的均匀程度,引入基于Voronoi图的均匀度计算[21]。首先将各感知节点构成Delaunay三角形;其次找出离散点周围所有三角形内心;然后沿顺时针方向将感知节点周围的内心连接起来,最后即得到各感知节点的Voronoi图,记为Vi,i=1,2,…,n,其面积分别记为SVi,i=1,2,…,n。
定义均匀度为一个区域内所有Voronoi图面积的标准差的倒数,即:
(6)
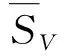
1.4 改进Kriging插值估计
根据Kriging算法的特点,感知节点的均匀程度决定插值估计的准确程度。本文改进Kriging在有限数量的感知节点下,根据地理位置的密集程度,在不同粒度下进行Kriging插值估计。理论分析表明,多粒度Kriging插值的算法复杂度会增加,但是通过该算法实现的构建效果较好、精度提升。
对于含有n个感知节点的战场区域,首先分别进行kr(r1=1,2,…,R)次聚类,即每次聚类处理产生r个聚类簇,其中每个聚类簇记为第krp(p=1,2,…,r)个待估计区域,则该区域的感知节点均匀度表示为:
(7)
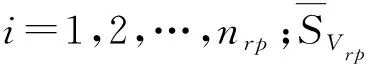
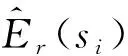
(8)
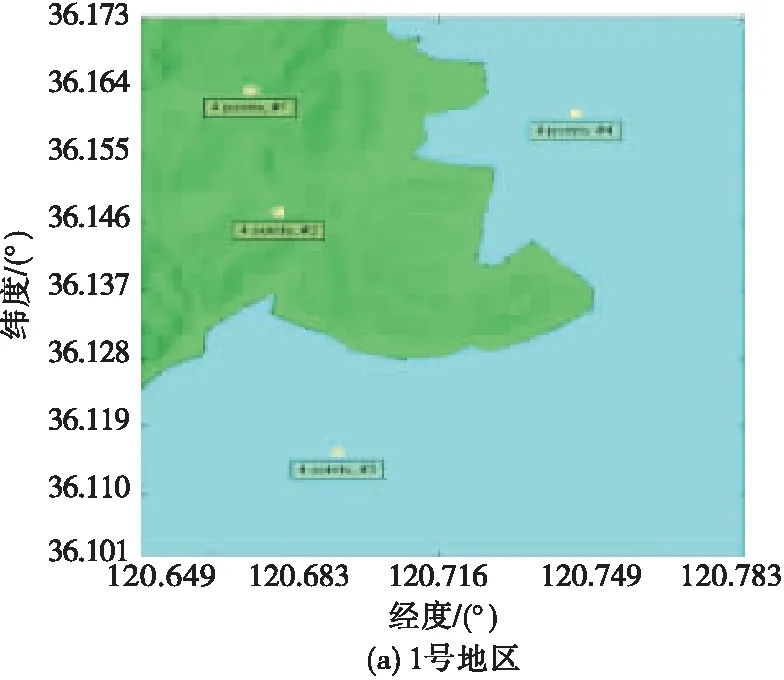
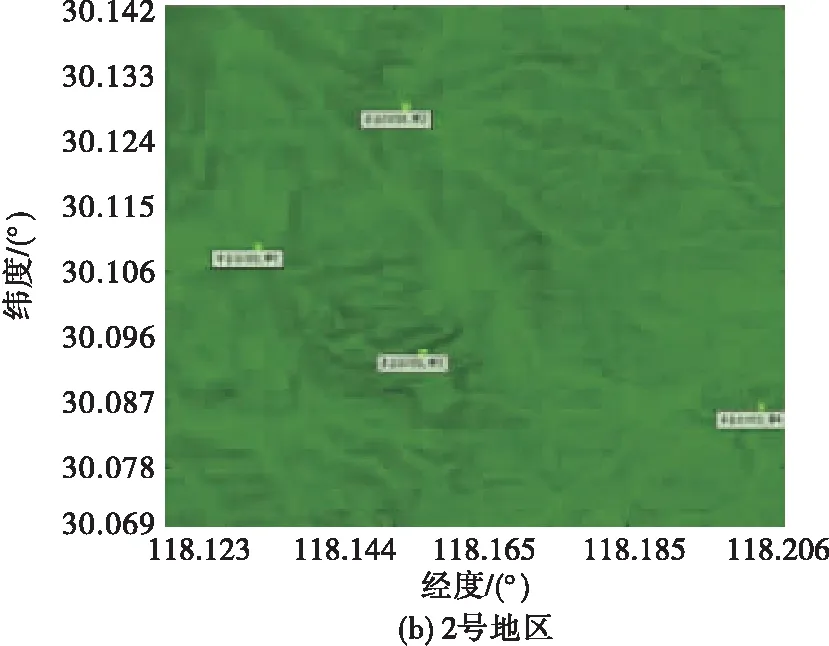
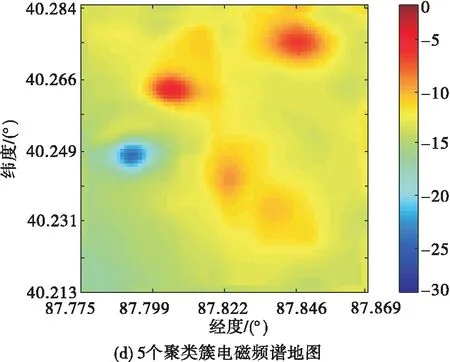
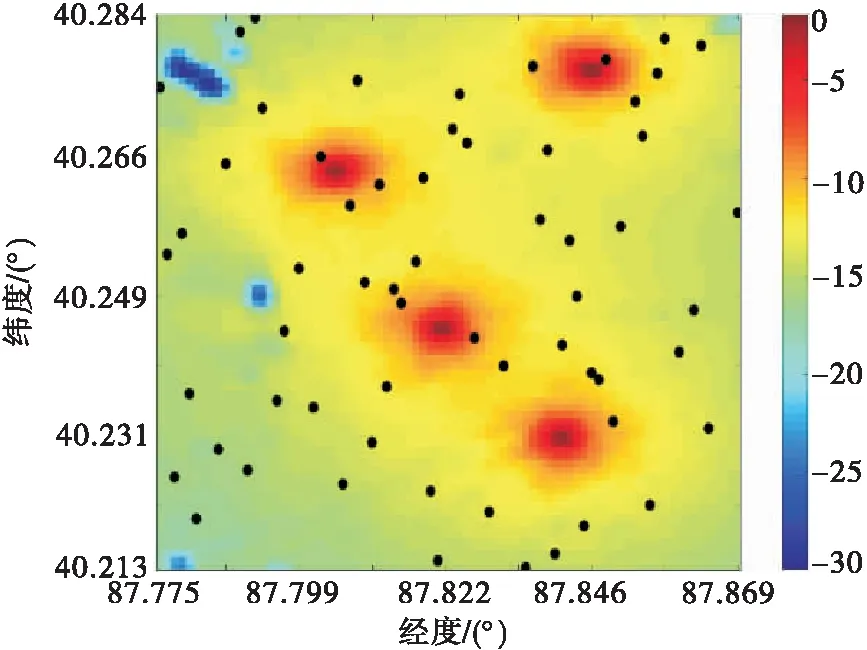
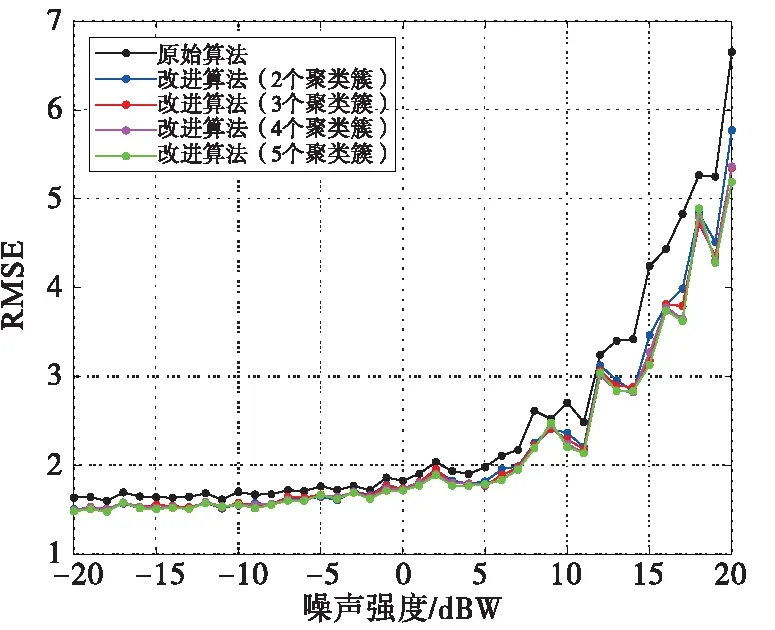
式中:Re表示未知点si均包含于每一次聚类得到的估计区域中的数量,Re (9) 通过引入了均匀度对原始算法进行改进,提高了单一Kriging插值算法的准确性,利用均匀度权重进行估计值整合,既增强了邻域内感知节点对未知点的作用,又考虑了邻域外感知节点的微弱影响。其具体的算法步骤见表1。 表1 算法步骤 对战场电磁环境进行建模,验证本文所提的结合K-means聚类和Kriging算法的电磁频谱地图构建算法的有效性。 首先在Wireless Insite无线电波传播仿真软件中进行仿真,选取多个面积为8 km×8 km的真实地形模拟战场环境,随机放置通信电台和感知节点。然后在图新地球4软件中分别选取了8 km×8 km的部分地区作为仿真环境,依次命名为1~4号地区,提取并输出其高程数据。将地形数据导入Wireless Insite,在1号和2号地区中添加Wet Earth和Dense Deciduous Forest in Leaf,1号地区的海水部分添加Sea Water,在3号地区添加覆盖Dry Earth,在4号地区中覆盖Dry Sand。在4个场景中设置了数个通信电台,其中所有通信电台均为正弦信号,中心频率为15 MHz,带宽为3 kHz,采用半波偶极子天线,发射增益和接收增益为0 dB,战场仿真场景部分参数见表2,仿真场景如图2(a)~(d)所示。在Wireless Insite仿真软件中布置80×80个等距分布的接收机测量电场强度,生成标准的电磁频谱地图,如图3(a)~(d)所示。 图2 不同地区地形及电台部署图 图3 不同地区标准电磁频谱地图 表2 战场仿真场景部分参数 最后在地图上随机选取60个感知节点作为算法的已知感知节点,获取感知节点的EFS值,导入MATLAB进行计算,在此基础上得到电磁频谱地图。 从Wireless Insite中提取各个仿真场景的电场强度值,导入MATLAB R2018b,在处理器为AMD R7-4800H、RAM为16 GB、GeForce RTX 2060的环境下运行。采用高斯模型作为变异函数模型,以聚类簇的个数为自变量,以各个仿真场景下的均方根误差(RMSE)为因变量,定义算法性能提升比α为: (10) 式中:RMSEi表示i个聚类下的克里金算法的RMSE;RMSEK为原始算法下的RMSE。 为更加有效地衡量算法在各个场景的应用效果,对60个感知节点进行了1 000次的独立抽取,根据计算结果生成不同仿真环境下聚类个数与RMSE的变化关系图,如图4所示。将多个聚类簇下的RMSE与原始算法的RMSE进行比较后,形成如图5所示的性能提升曲线。与图4相比,图5消除了平均值带来的影响,算法性能提升更为直观。实验中,聚类数为3和4时的RMSE分别为8.809和8.812,性能提升比呈现下降趋势,蓝线代表山地地形,场强分布杂乱,插值较为困难,从而造成算法效果提升不高。同时,为了评估各个仿真场景下应用算法的稳定性,计算每次聚类的RMSE的标准差,1号、2号、3号和4号在4个仿真环境下得到的RMSE标准差分别为0.204、0.397、0.229和0.290。经过比较可以看出,该算法相对于原始算法RMSE可降低2%~5%。性能提升程度与地形有一定关系,地形越简单,电场分布的规律性越好,构建精度越高,算法应用更为稳定。 图4 聚类个数与RMSE的变化关系图 图5 性能提升曲线图 利用上述算法对目标区域进行插值估计,从4号地区随机选取60个位置放置感知节点,分别在原始算法、改进算法(3个聚类簇)、改进算法(5个聚类簇)下生成该地区电磁频谱地图,如图6(a)~(d)所示。 图6 不同算法下4号地区标准电磁频谱地图 随着聚类个数的增加,目标区域电磁频谱地图的RMSE逐步减小,原始算法、改进算法(3个聚类簇)和改进算法(5个聚类簇)的RMSE分别为1.77、1.76和1.70,改进算法相对于原始算法分别提高了0.5%和3.6%,证明本文所提算法在构建电磁频谱地图上具有可行性,能更好地反映电磁环境的真实情况。 在同样的实验条件下,对算法的复杂度进行分析,不同粒度下的算法复杂度及其对应的运行100次平均时间见表3。 表3 不同粒度下算法复杂度及其运行时间 由于介电常数变化、障碍物折射等客观不定因素影响,电场强度会在一定范围内波动,基于对算法的容错性分析,验证算法应对环境的适应能力。根据2.2节的实验现象,选取地形较为简单的4号地区作为实验场景。在生成的随机感知节点中,随机选取一组感知节点作为后续实验的固定已知点,感知节点分布见图7。 图7 感知节点分布图 随后,在标准电磁频谱地图数据上采集感知节点的电场强度值,以噪声强度代表由于客观因素造成的电场强度数据误差,对数据进行不同程度的加噪处理,将处理后的数据代入本文所提算法,在不同粒度下进行验证,实验结果见图8。 图8 噪声强度对构建精度的影响 根据实验结果可知,本算法在噪声强度较小时,RMSE变化平稳,聚类个数对构建精度影响不大,但原始算法的效果普遍低于本文算法。当噪声强度增大时,RMSE逐渐加大,噪声强度小于8 dBW时,RMSE保持平稳;噪声强度大于8 dBW时,RMSE明显增大,改进算法相对于原始算法有较好优势,表明本文算法在强噪声下的构建精度更高,容错能力更强。 从以上实验得知,本文算法在4个场景中应用效果较之原始算法都有较大提升,地形越复杂,提升效果越明显。通过算法性能分析的实验,证明本文算法在细粒度下构建精度有所提升,且聚类个数越多,粒度越细,性能提升比越大。根据大量实验可得,聚类数为2~3时,时间性能比相对较大,可以为后续运用提供建议。此外,通过容错性分析实验表明,算法对于8 dBW以下的噪声强度有较好的适应性,对电磁频谱地图构建精度影响不大,而感知节点数量不足的情况下,该算法可以通过划分更为精细的粒度,改善构建精度,证明本文算法鲁棒性强,应用能力广泛。 本文旨在探究战场条件不利情况下提高电磁频谱地图的构建精度,考虑到感知节点分布不均影响电磁频谱地图构建效率,提出了一种基于Kriging算法的多粒度电磁频谱地图构建技术,引入了多粒度插值的思路和均匀度的概念改进Kriging算法,以Voronoi图的原理计算了各个粒度区域的均匀度,并将其作为数据融合的权值,实现了在感知节点有限的情况下生成更为精确的电磁频谱地图,并验证了算法的有效性。
1.5 算法复杂度分析
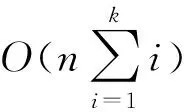
2 仿真实验分析
2.1 仿真场景构建
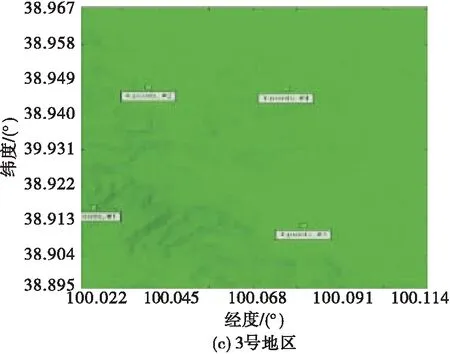
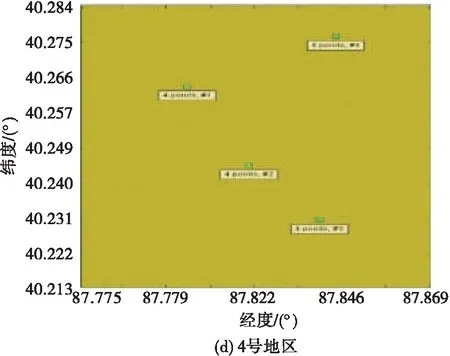
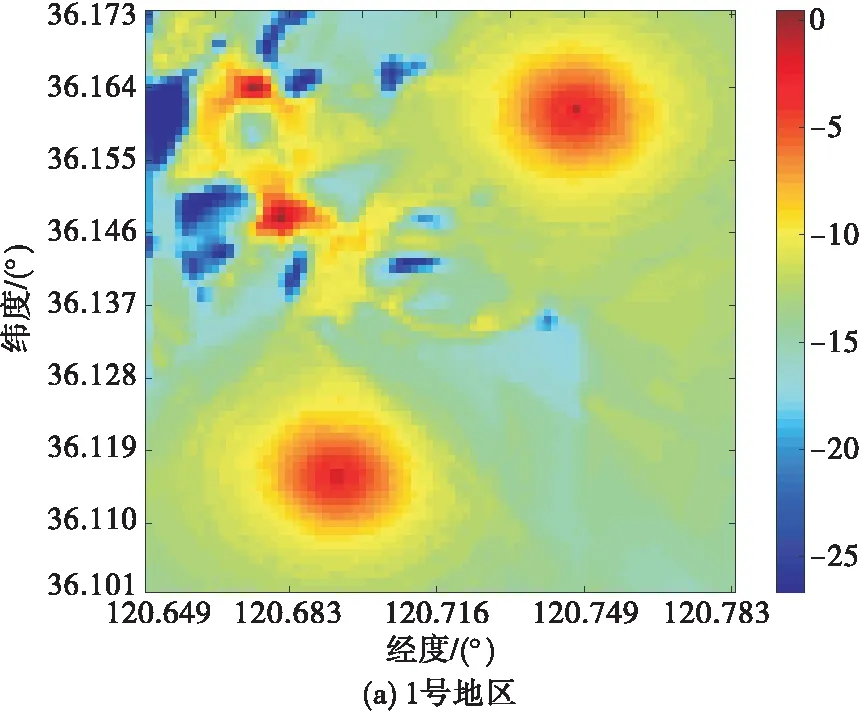
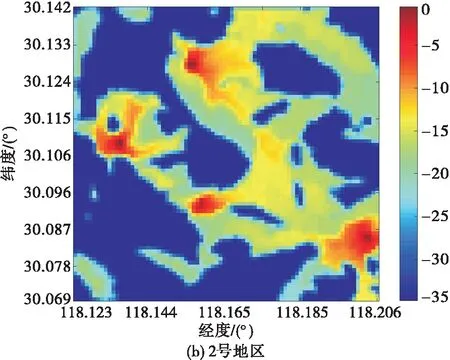
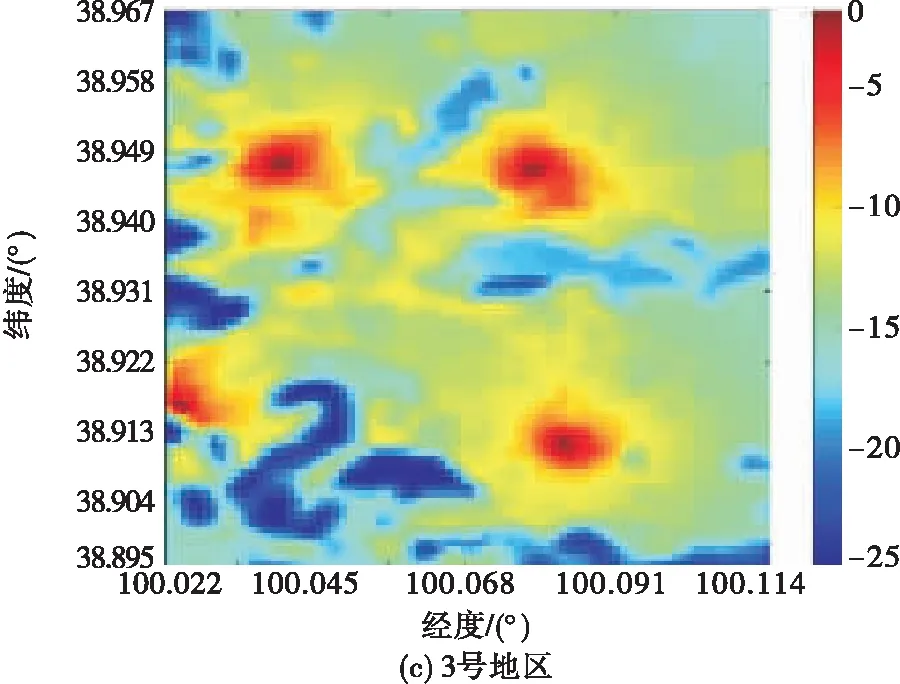
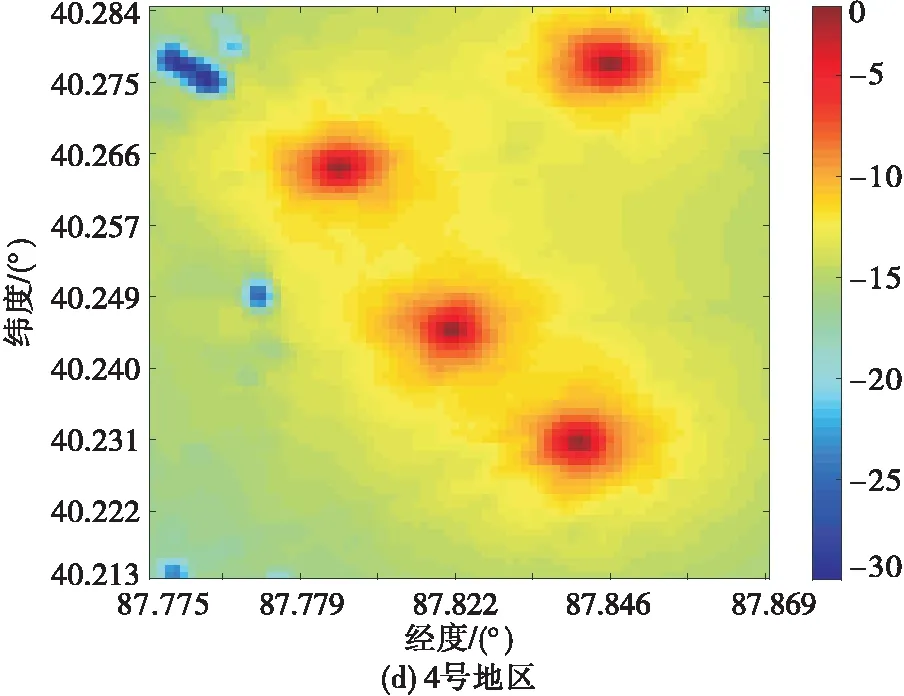
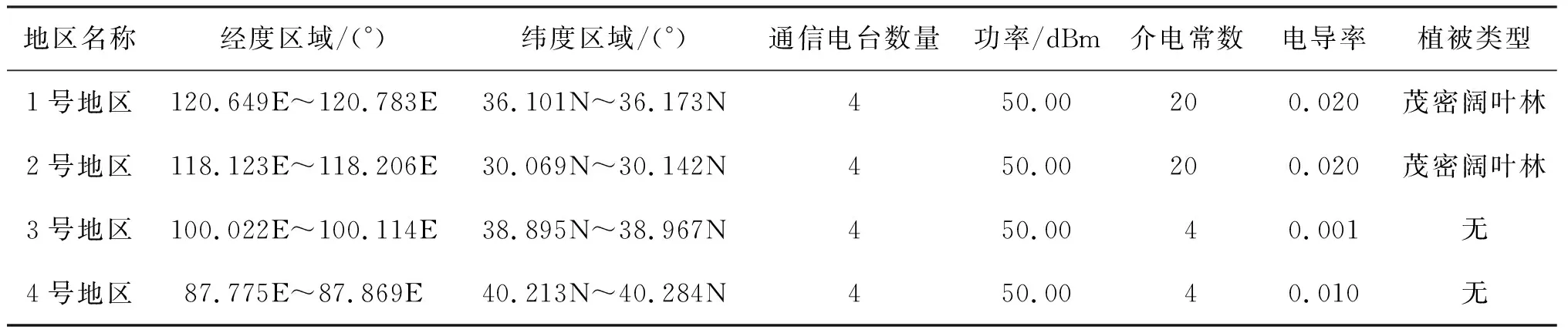
2.2 电磁频谱地图构建性能分析
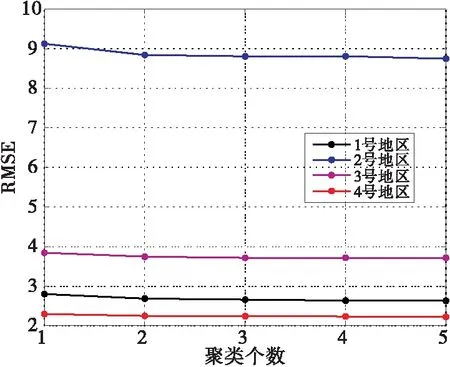
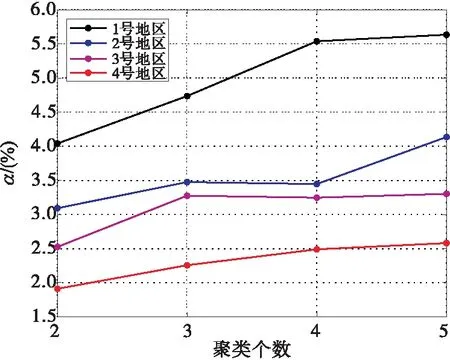
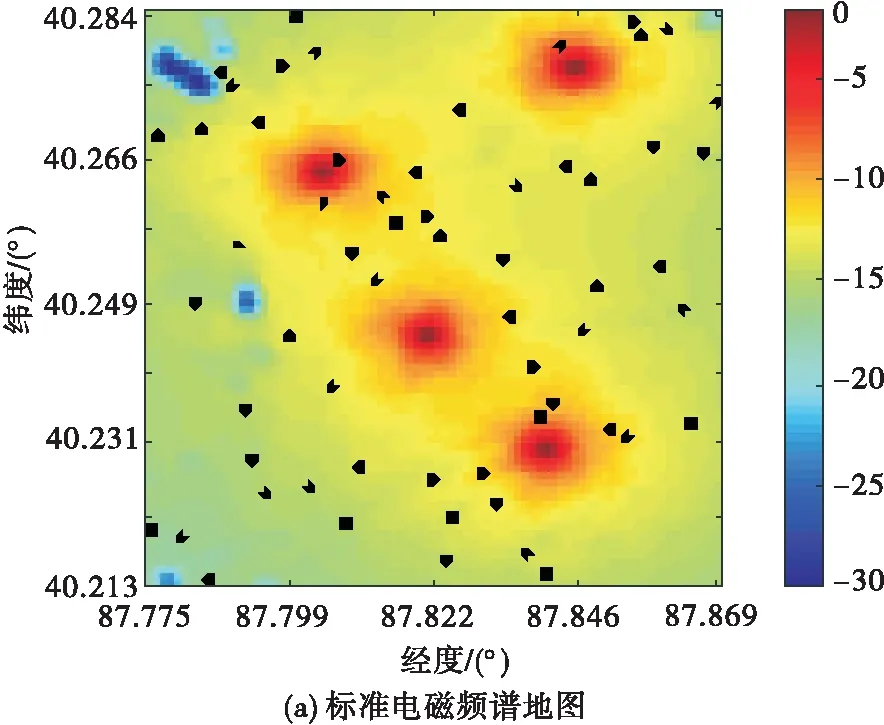
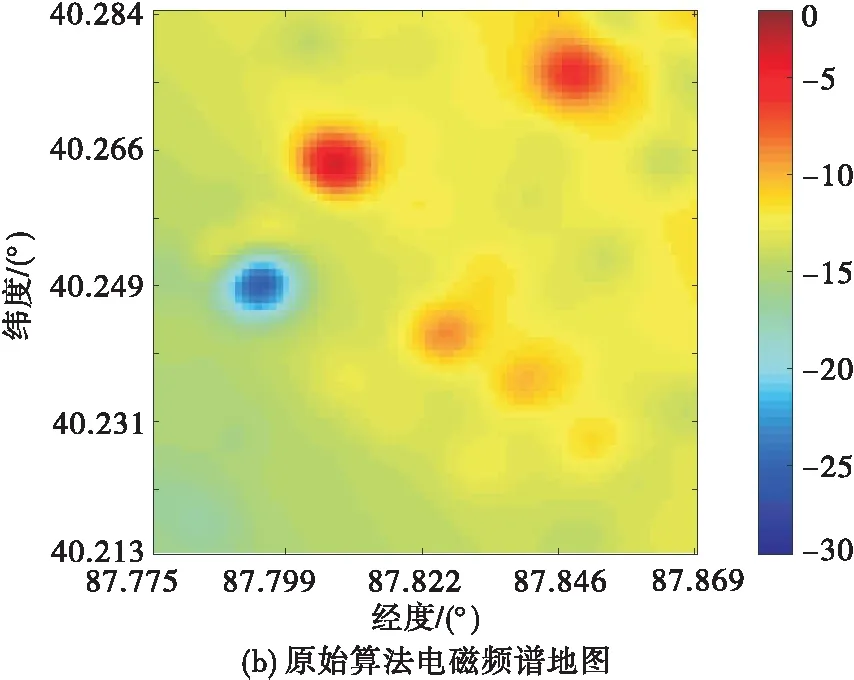
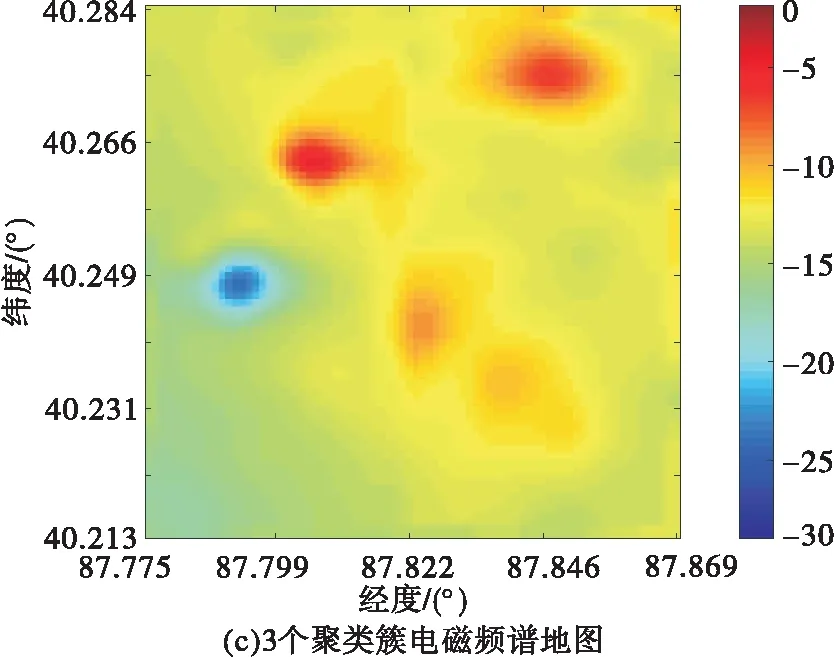

2.3 算法容错性分析
3 结语

