滑动式广义延拓插值法在GLONASS钟差插值中的应用

化希瑞

( 中国铁路设计集团有限公司, 天津 300142 )

0 引 言

卫星钟差是指卫星搭载的卫星钟与标准时的差值，当某颗卫星的钟差达到1 ms时，对测距的影响会达到300 km[1]，所以卫星钟差的精度对卫星导航定位的精度影响很大. 随着卫星定位技术的发展，接收机的采样间隔也逐渐变密，往往需要对钟差数据进行插值才能满足实际应用的需求.

目前国内外在对卫星钟差数据进行插值处理时常用的插值方法为Lagrange插值法[2]和切比雪夫多项式拟合法[3]，虽然这两种传统的插值方法插值处理效果都很好，但仍然存在局限性，利用Lagrange插值法进行插值时，随着插值阶数的增加，会产生“龙格现象”，而切比雪夫多项式拟合法虽然避免了“龙格现象”，但在拟合过程中会丢失部分高精度数据，导致插值精度的降低.

广义延拓插值法是将插值方法和拟合方法进行有效地组合，这种插值方法在对离散数据的插值处理中有很好的应用效果，并且在对GPS、北斗卫星导航系统(BDS)卫星钟差数据的处理中取得了一定的成果[4-6]. 但在对GLONASS中的应用研究较少，本文尝试利用广义延拓插值法、Lagrange插值法和切比雪夫多项式拟合法对GLONASS的钟差数据进行插值，为进一步提高插值效果，对这三种插值方法都进行了滑动，通过对插值结果的对比和分析，得出了一些结论.

1 卫星钟差插值方法

1.1 广义延拓插值法

广义延拓插值法在对离散数据进行处理时，将其分为若干个不重叠的单元域，在每个单元域内进行插值计算，对单元域进行延拓得到延拓域，在延拓域内进行拟合，得到同时满足两个条件的逼近函数[7]，对插值和拟合方法的优点进行了结合.

同时，Ue(x) 也要满足 Ωe上的插值条件

式中，i=1,2,···,r.

将式(2)和式(3)合写，得到

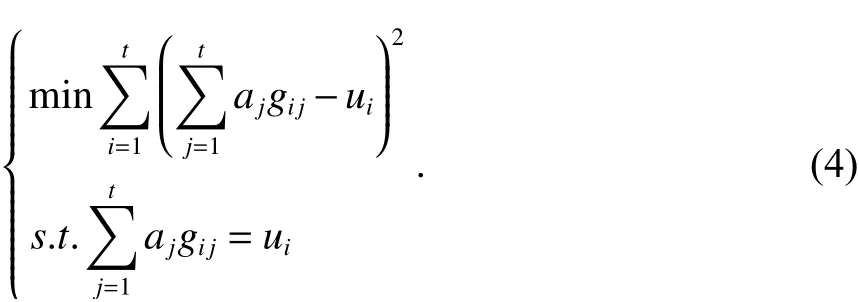
通过利用拉格朗日乘数法，对式(4)进行计算，得到式(1)中的a1,a2,···,at，从而得到 Ωe的插值函数.再对不同单元域分别进行计算，得到m个插值函数，从而得出整个数据域 Ω 的逼近函数U(x) 为

1.2 Lagrange插值法

Lagrange插值法的数学模型简单，在数据处理中的应用十分广泛.

其插值算法如下[8]：

在n+1 个 不同插值点x0,x1,···,xn处存在插值多项式Ln(x) ，使得

构造n次插值多项式

1.3 切比雪夫多项式拟合法

切比雪夫多项式拟合法是比较常用的数据插值方法，利用区间上已知数据拟合出多项式函数，将这个多项式函数对区间内的未知数据进行插值[9].

对于 [t0,t0+Δt] 上 的钟差数据，t0为参考历元，Δt为拟合区间长度. 将t∈[t0,t0+Δt] 表示为 τ ∈[-1,1] ，得到

t时刻的钟差为

式中：n为拟合阶数；Ci为待求系数，根据已知数据通过最小二乘法进行拟合得到Ci；利用切比雪夫多项式拟合法递推公式可以确定Ti(τ) ，即

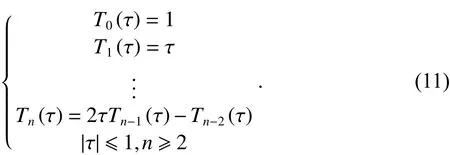
将所求得的Ci、Ti(τ) 代入式(10)中，可以得出未知点钟差数据.

1.4 滑动式插值算法

由于插值区间的固定，在进行插值时，不同插值区间内得到的数据呈现出跳跃，不利于插值结果精度. 利用滑动式插值法进行插值时，可以实现当插值点滑动时，插值区间也随之滑动，从而保证所计算的插值点始终处于插值区间的中间，提高了插值结果的精度[10]. 所以本文在对GLONASS钟差数据进行插值计算时，采用的三种插值方法都利用了滑动式插值法.

2 算例分析

本文采用由德国地球科学研究中心下载的2021-06-01—06-03三天历元间隔为5 min的GLONASS精密钟差数据(https://www.gfzpotsdam.de/en/section/space-geodetic-techniques/topics/gnss-services/)，分 别利用滑动式广义延拓插值法、滑动式Lagrange插值法和滑动式切比雪夫多项式拟合法将5 min的钟差数据插值为30 s，并与30 s的精密钟差数据进行对比，使用均方差和平均绝对误差衡量插值方法的精度，通过对三天内所有运行中的GLONASS卫星插值结果的统计，分析三种滑动式插值方法在GLONASS钟差数据处理中的应用效果.

2021年6月1日共有20颗GLONASS卫星有钟差数据. 利用滑动式Lagrange插值法、滑动式切比雪夫多项式拟合法和滑动式广义延拓插值法对这20颗卫星的钟差数据进行插值，设置最大插值节点数为20，在3～20中逐次选取所有的插值节点，每次选定插值节点数后，再对应插值节点数逐次选取不同的阶数，最终确保所有的参数组合都进行计算．此过程利用MATLAB软件实现. 统计出每种参数组合对应的插值精度，通过对每种插值精度的对比，选取精度最优时的参数组合，得到其插值结果如表1～3所示.

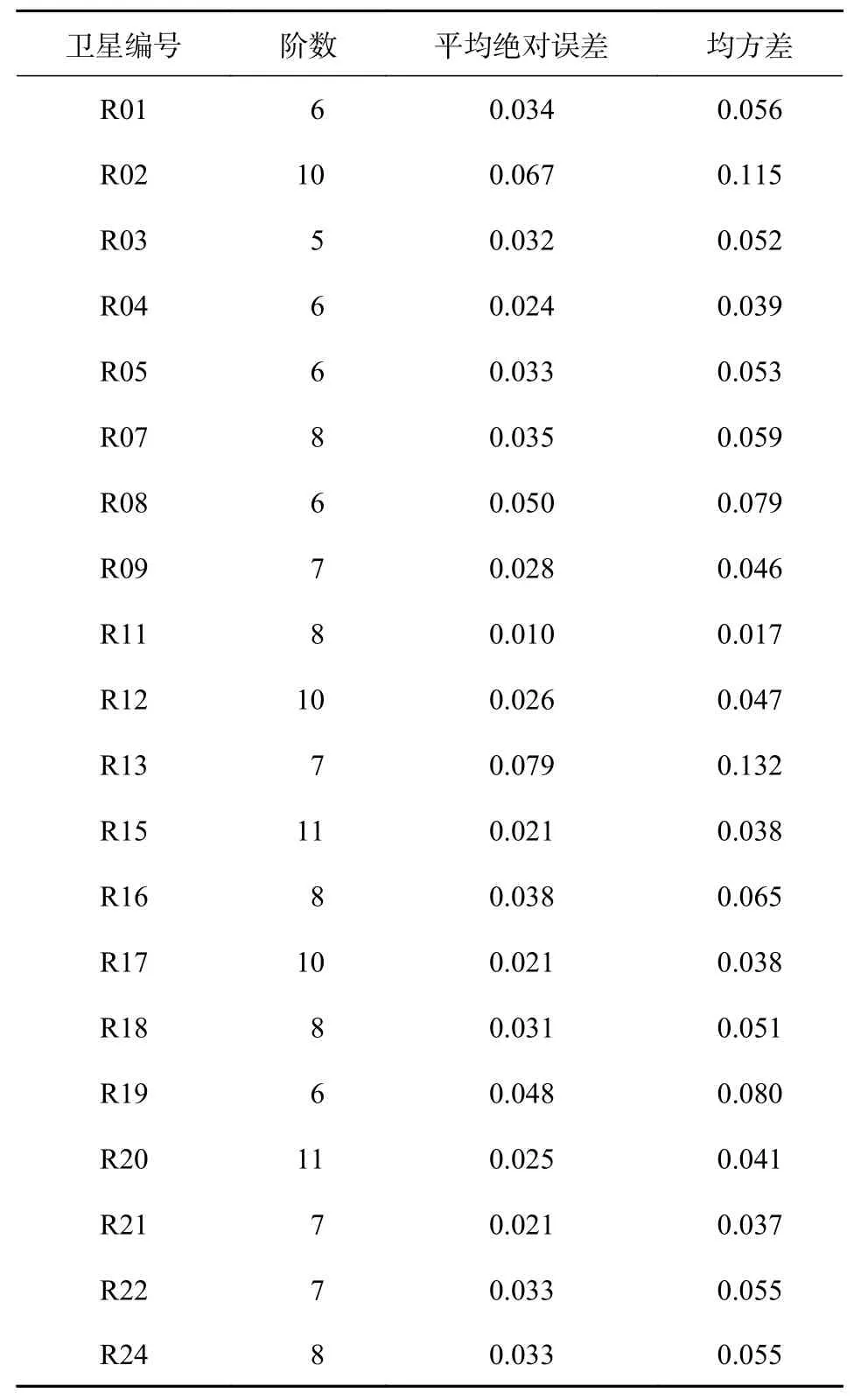
表1 滑动式Lagrange插值法插值结果

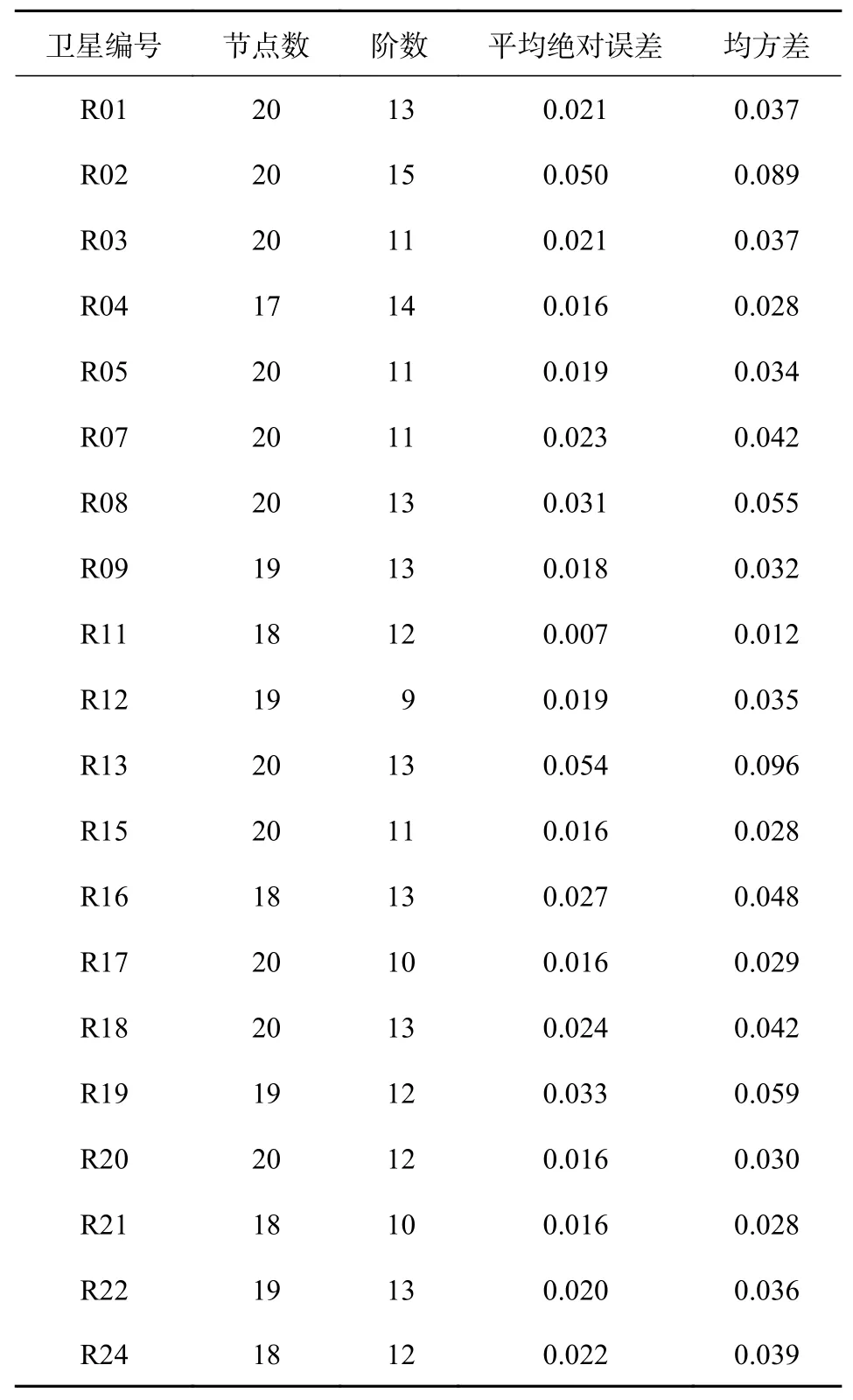
表2 滑动式切比雪夫多项式拟合法插值结果

表3 滑动式广义延拓插值法插值结果

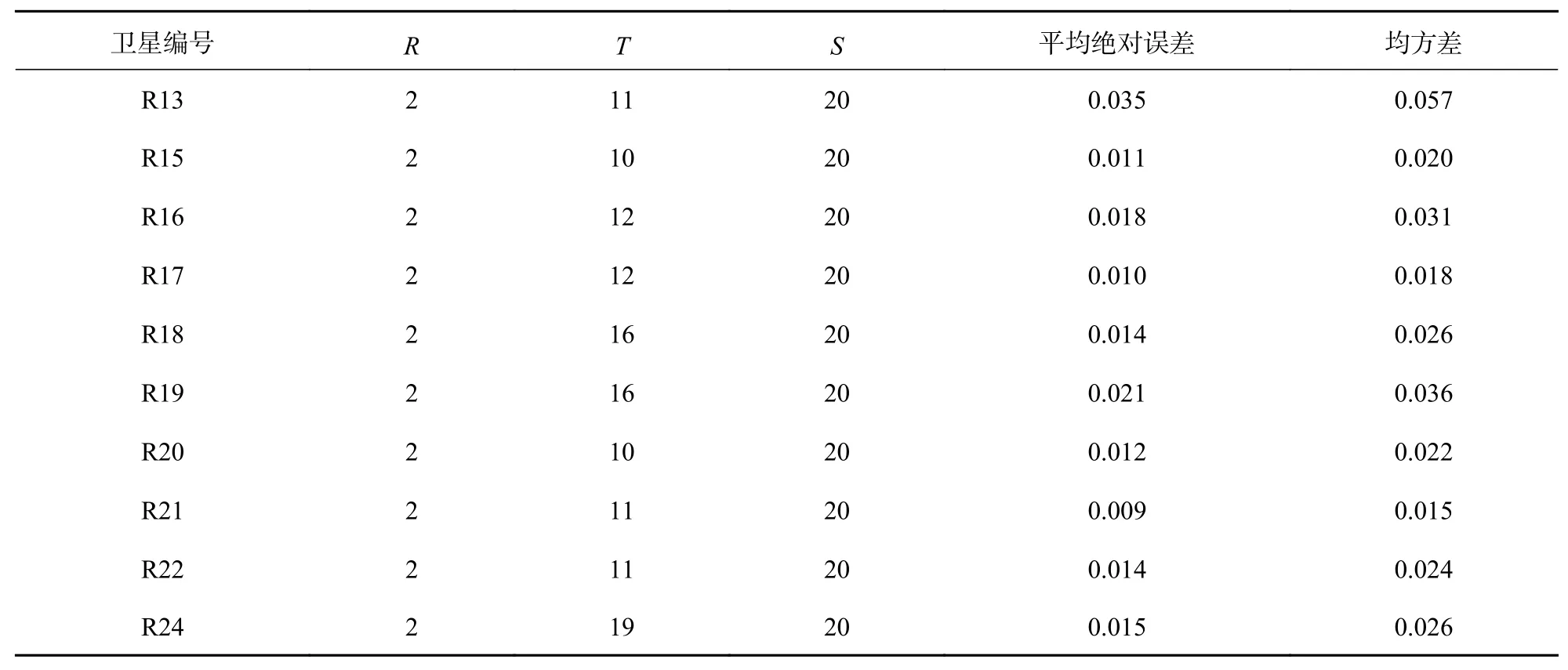
表3（续）

从表中可以看出，对于GLONASS中的不同卫星，利用同一种插值方法进行插值时，其最优参数组合并不一致；利用滑动式Lagrange插值法进行钟差数据处理时，插值精度并不会随着插值阶数的增加而增加；当滑动式切比雪夫多项式拟合法和滑动式广义延拓插值法在分别得到最优精度时，所配置的参数组合中的节点数虽然相差不多，但滑动式广义延拓插值法的插值精度明显高于滑动式切比雪夫多项式拟合法，这说明滑动式切比雪夫多项式拟合法在对钟差数据的处理中，很可能丢失了部分高精度的钟差数据.

为了更直观的对这三种插值方法的均方差和平均绝对误差结果进行对比，图1～2分别绘制了相应的插值精度直方图.

图1 2021年6月1日平均绝对误差精度对比

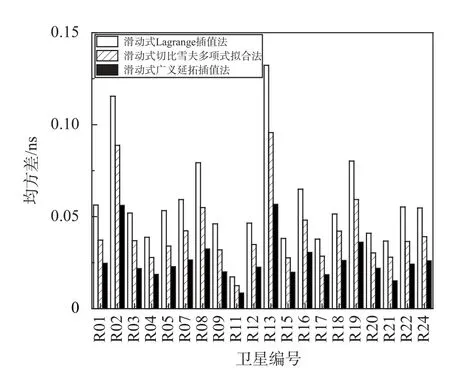
图2 2021年6月1日均方差精度对比

分别计算这三种插值方法对20颗GLONASS卫星钟差数据的均方差插值结果，可以得出：三种插值方法的均方差平均插值精度分别为0.058 ns、0.042 ns和0.026 ns；利用滑动式广义延拓插值法的插值精度较滑动式Lagrange插值法、滑动式切比雪夫多项式拟合法分别提高了54%和37%，可见滑动式广义延拓插值法的插值结果离散程度最低，插值精度最高，应用效果最好.

为了进一步探讨这三种插值方法的最优参数组合和验证滑动式广义延拓插值法的插值精度，在相同条件下，分别利用这三种插值方法对2021年6月2日—3日的GLONASS卫星钟差数据进行处理.

分析同一颗卫星这三天的插值结果取最优插值精度时所对应的参数组合，以5颗卫星为例，其结果如表4～6所示.

表4 2021年滑动式Lagrange最优插值阶数

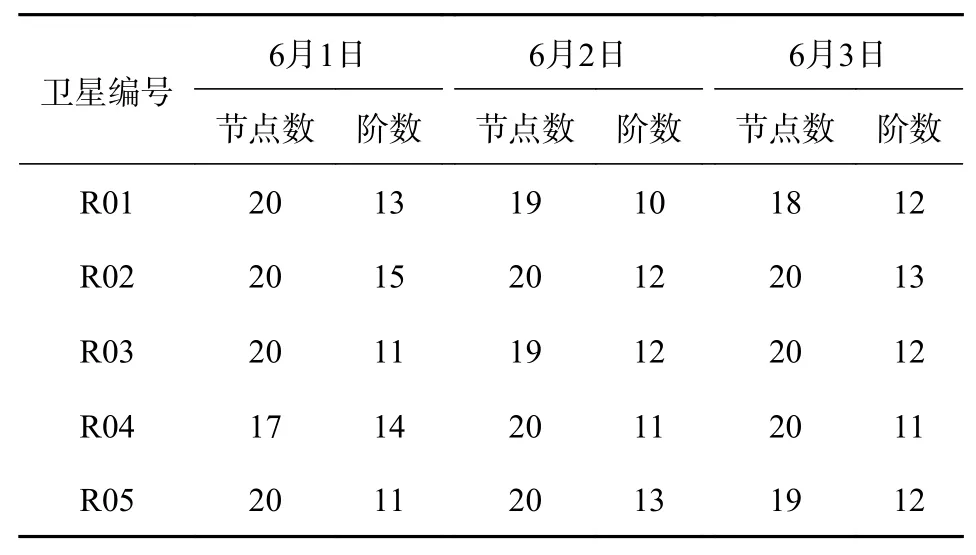
表5 2021年滑动式切比雪夫多项式拟合法最优参数组合

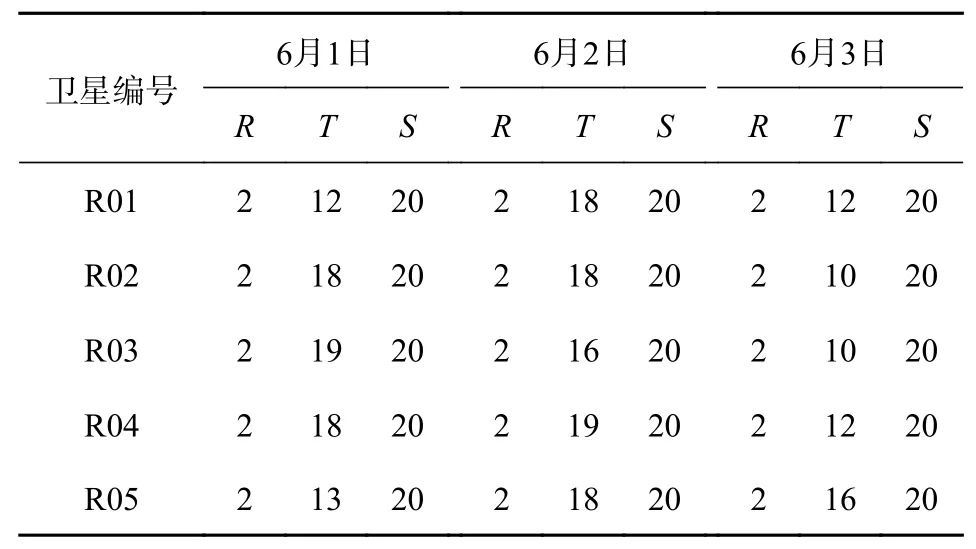
表6 2021年滑动式广义延拓插值法最优参数组合

由表4～6可知，对于同一颗卫星不同时期的钟差数据，利用同一种插值方法进行插值时，其最优参数组合也不一致.

根据2021年6月2日—3日的GLONASS卫星钟差数据的插值结果绘制插值精度直方图，如图3～4所示.

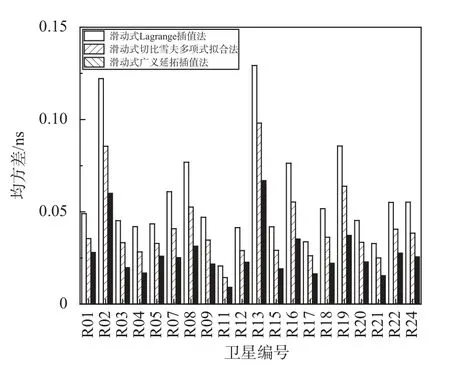
图3 2021年6月2日均方差插值精度对比

从图中可以直观的看出，在对2021年6月2日—3日的GLONASS卫星钟差数据进行插值时，滑动式广义延拓插值法的插值精度仍然要高于其他两种插值方法.

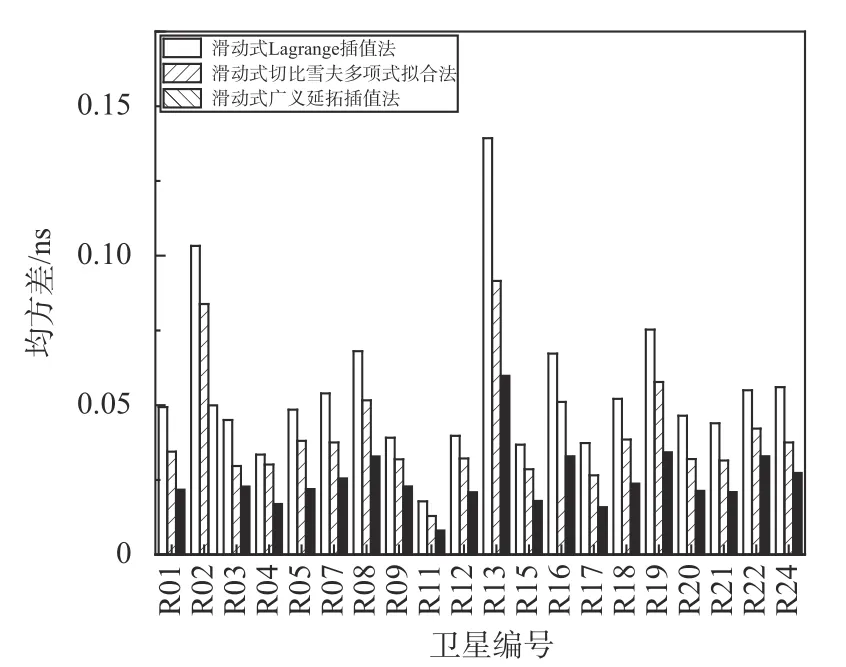
图4 2021年6月3日均方差插值精度对比

3 结 论

1)不同的GLONASS卫星在不同时期利用滑动式Lagrange插值法、滑动式切比雪夫多项式拟合法和滑动式广义延拓插值法这三种插值方法取得最优插值精度时所对应的参数组合并不相同，表明当进行钟差插值计算时，不能套用固定的参数组合，必须对参数组合择优后插值.

2)当对5 min的GLONASS卫星钟差数据插值到30 s时，滑动式Lagrange插值法、滑动式切比雪夫多项式拟合法和滑动式广义延拓插值法这三种插值方法虽然都能满足精度要求，但滑动式切比雪夫多项式拟合法的插值精度要高于滑动式Lagrange插值法，而滑动式广义延拓插值法将这两种方法进行了组合，其插值结果离散程度最低，插值精度最高.

3)通过对随机连续三天的GLONASS卫星钟差数据进行插值，都能得出一致结论，即滑动式广义延拓插值法的插值精度最高，这说明滑动式广义延拓插值法在对GLONASS卫星钟差数据的插值中具有很好的应用价值.

致谢：感谢德国地球科学研究中心提供的GLONASS精密钟差数据！