GNSS载噪比反演船载气象要素传感器距水面高度
仇志金,胡桐,邹靖,李志乾,王波
( 1. 齐鲁工业大学(山东省科学院)海洋仪器仪表研究所, 山东 青岛 266061;2. 山东省海洋环境监测技术重点实验室, 山东 青岛 266061;3. 国家海洋监测设备工程技术研究中心, 山东 青岛 266061 )
0 引 言
海面蒸发波导参数的监测预报是船载无线电气象系统的典型应用场景[1-2]. 目前,普遍采用建立在海上大气边界层相似理论基础上的块体参数化方法(Bulk aerodynamical method)获取近海面大气折射率廓线. 船载气象要素传感器的测量高度是块体参数化方法的必要参数. 由于船舶吃水深度往往随船舶载重量、海况和航速航向等因素动态变化,安装于船体上层建筑的气象要素传感器距水面高度随之发生改变[3].气象要素传感器距水面高度的系统偏差直接影响蒸发波导高度监测预报结果的准确性[4].
用于获取气象要素传感器距水面高度的非接触式测距方法主要包括图像分析测量、激光测量、声学测量等. 图像分析测量利用船载光学摄像机采集吃水线多帧图像,通过数字图像处理换算距离,测量结果受天气条件和能见度影响较大[5]. 激光测量利用激光方向性和相干性好的特点,通过单机多点或多机光幕测量反射光信号时延、相位等特征,测量精度高,但设备成本高且受海上高温、高湿、高盐环境影响较大[6].声学测量基于回声测距原理,通过测量回波信号时延、角度计算距离,在海上受波浪破碎飞溅以及雨水的影响较大[7]. 以上测距方法各具优缺点,因此需要根据实际安装环境、应用场景和设备安装维护成本综合选择适宜的测量方法与仪器设备.
目前,船舶普遍安装有全球卫星导航系统(GNSS).GNSS在船舶自主导航、进港引水、航路监管等方面发挥着重要作用. GNSS系统主要包括美国GPS、俄罗斯GLONASS、欧洲Galileo、我国北斗卫星导航系统(BDS),已有100多颗卫星在轨运行. 由于导航卫星使用的L频段微波信号对雨雪天气不敏感,具有信号覆盖广、全天候的特点,近年来利用GNSS信号监测大气水汽分布[8]、建筑物结构变形[9]、陆面积雪厚度与土壤湿度[10]、海表有效波高[11]等应用场景逐渐增多[12]. 本文利用船载GNSS接收机接收卫星信号,观测信号载噪比(CNR)时间序列,分析卫星直射信号与水面反射信号相干性,反演天线相位中心距水面高度,根据气象要素传感器与GNSS天线之间的几何关系换算气象要素传感器距水面高度,简化安装维护专用测距设备引入的系统复杂度.
1 反演方法
水面是良好的GNSS信号反射面. GNSS反射信号在接收端常被视为多路径干扰,采用抗多径天线和基带信号处理算法进行抑制. 为提高接收信号强度,船载GNSS天线一般安装于桅杆或舰桥顶部开阔区域. GNSS接收机接收的卫星直射信号不可避免地受到水面反射信号的影响. GNSS信号经水面反射后,极化形式由右旋圆极化变为左旋圆极化,反射信号相位和幅值的变化承载着反射表面粗糙度等物理特征[13].对于GNSS接收机跟踪的某颗卫星而言,GNSS接收机接收的是其直射信号与水面反射信号的叠加信号.随卫星仰角的持续增大或减小,直射信号与反射信号的相干性体现为接收信号CNR的波动特性,如图1所示.
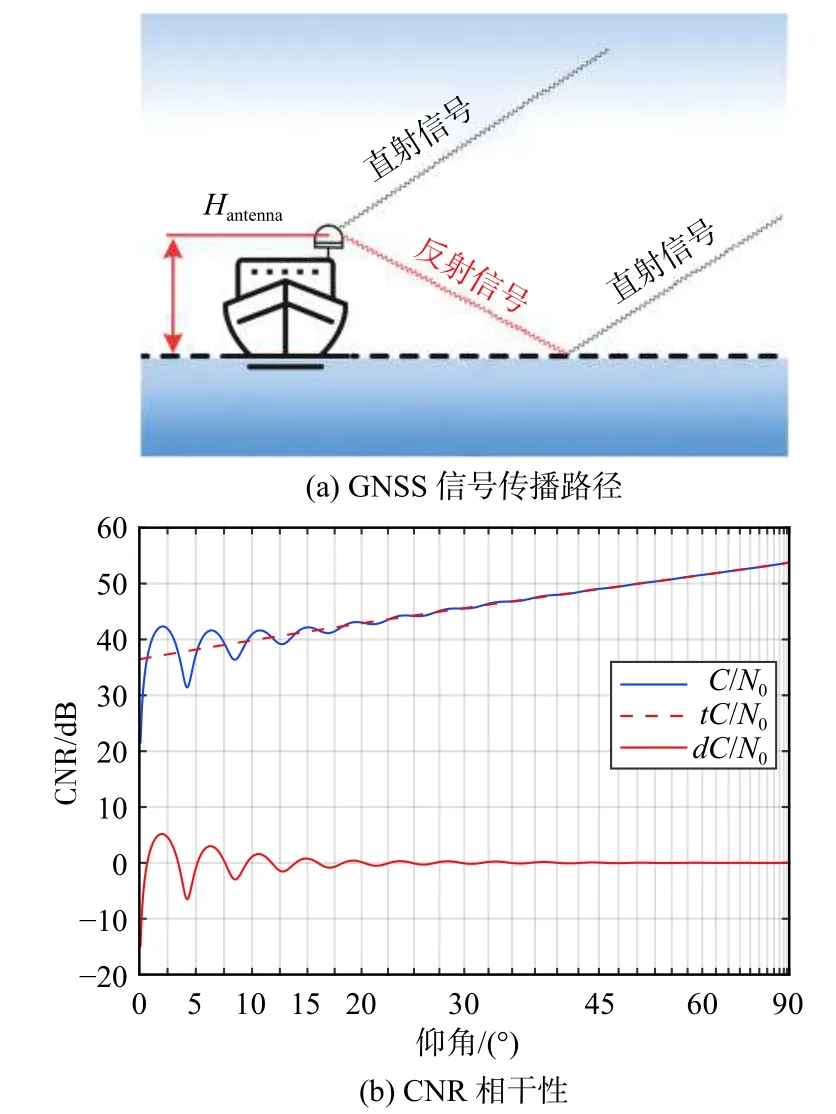
图1 GNSS信号路径与CNR相干性
GNSS接收信号CNR,记作C/N0. 包括由直射信号造成的趋势项,以及由直射信号与反射信号相干性造成的波动项[14],即
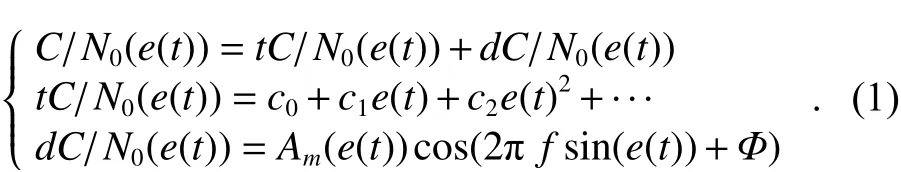
式中:t为观测时刻;e(t) 为t时刻卫星仰角;C/N0(e(t))为对应不同仰角的CNR时间序列;tC/N0(e(t)) 为CNR时间序列中由直射信号造成的趋势项,一般采用二阶或三阶多项式表示;dC/N0(e(t)) 为CNR序列中由直射信号与反射信号相干性造成的波动项;Am(e(t)) 为波动项振幅;f为直射信号与反射信号的相干频率;Φ为直射信号与反射信号的相位偏移.
船载GNSS接收机捕获并跟踪卫星信号,随卫星仰角的升高或降低,C/N0(e(t)) 观测时间序列大致呈抛物线型. 采用二阶多项式拟合可从C/N0(e(t)) 观测时间序列中去除卫星直射信号造成的趋势项tC/N0(e(t)) .C/N0(e(t)) 与tC/N0(e(t)) 的 残 差即dC/N0(e(t)) . 直 射 信号与反射信号相干性造成的dC/N0(e(t)) 波动频率为

式中:Hantenna为GNSS天线相位中心距离反射面的垂直高度; λ 为卫星信号载波波长. 对dC/N0(e(t)) 作频谱分析可求出频率f. 由于e(t) 并非等间隔采样,即低仰角卫星的仰角变化速率小于高仰角卫星的仰角变化速率,通常采用 Lomb Scargle周期谱分析方法(简称LSP分析)从给定仰角范围的一段dC/N0(e(t)) 观测时间序列中提取频率f,计算GNSS天线相位中心到反射面的垂直距离Hantenna.
GNSS天线相位中心与船载气象要素传感器垂直高度差值Hoffset为已知量. 利用图2所示几何关系,船载气象要素传感器距水面高度Hsensor可表示为
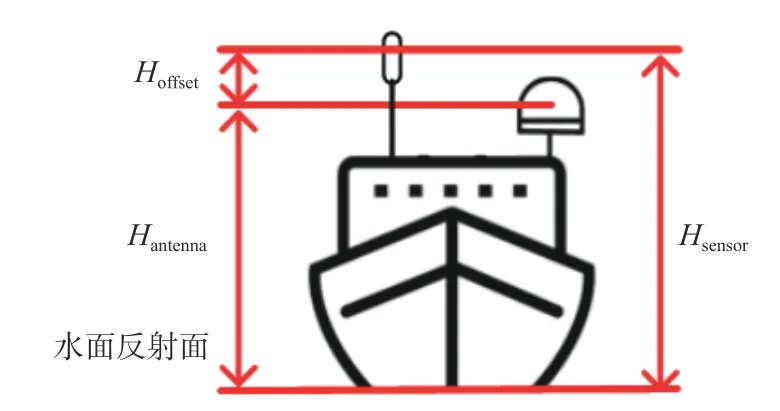
图2 反演变量几何关系
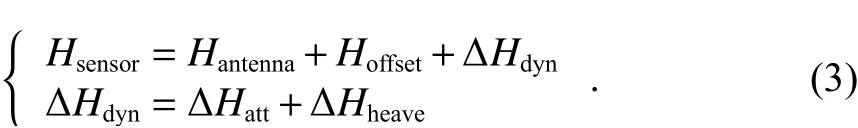
式中: ΔHdyn为受风、浪、流影响,船体运动产生的GNSS天线相位中心在垂直方向的位移; ΔHdyn主要包括船体纵横摇造成的位移分量 ΔHatt和船体升沉造成的位移分量 ΔHheave. 前者由惯性测量单元(IMU)测量船体纵横摇角度,通过欧拉角旋转获得;后者通过IMU或GNSS进行测量.
船舶航行过程中,船载气象要素传感器距水面高度均值随船舶载荷、燃油消耗以及水体密度的变化而变化. 上述反演算法的计算过程随观测卫星列表的更新而不断迭代.
2 趸船实验验证
为了验证上述船载气象要素传感器距水面高度反演方法的有效性,于2019-06-02—2019-07-30在山东省科学院海洋仪器仪表研究所海洋实验站进行了趸船实验. 实验期间,仅采集GPS单系统卫星信号CNR时间序列.
2.1 实验环境
趸船实验平台位于青岛市西部海滨,该实验平台长42 m,宽19 m,建有三层结构用于模拟船舶上层建筑,如图3所示. GNSS天线安装于桅杆顶部,距设计水线所在平面的垂直高度Hantenna为14.9 m. GNSS接收机安装于最上层舱室内,采用串口连接工控机.工控机采集、处理并存储GPS卫星L1单频CNR时间序列,通过反演程序计算GNSS天线相位中心距水面垂直高度Hantenna. 实验期间在桅杆横桁安装超声测风传感器,同步采集海表风速数据. GNSS接收机与超声测风传感器的采样频率均为1 Hz.
相对于实船平台,趸船平台纵横摇与升沉造成的GNSS天线相位中心距水面的垂直位移 ΔHdyn基本可以忽略,式(3)可简化为

因Hoffset已知,图3为本次实验采用直接量化Hantenna与Hantenna偏差的方式对本文提出的反演方法有效性进行验证.

图3 趸船实验概况
2.2 实验数据
工控机接收GNSS接收机发送的NMEA标准格式数据,由$GPGSV语句提取当前可见卫星信号CNR. 本实验使用的GNSS接收机输出的NMEA标准格式中,CNR分辨率为0.25 dB-Hz. 为了提高反演dC/N0波动曲线频率的准确性,在工控机端使用RTKLIB以二进制格式接收GNSS接收机数据流,将CNR分辨率提高至0.1 dB-Hz,然后以NMEA标准格式输出并存储.
反演程序接收RTKLIB输出的NMEA标准格式数据,更新当前可见卫星列表及其CNR时间序列. 当新的可见卫星加入列表后开始记录CNR;当某颗可见卫星的仰角达到极大值或该卫星退出列表后触发LSP分析,解算GNSS天线相位中心距水面垂直高度Hantenna.
实验场周围(方位角为0°~120°)矗立有若干高层建筑会阻碍低仰角卫星信号的正常接收,为确保GNSS天线接收低仰角反射信号的镜面反射点位于水面,选择方位角为120°~360°的CNR观测数据. 其中,方位角300°~360°岸边环境无高层建筑遮挡,故未在以方位角筛选观测数据的步骤中予以剔除. 对CNR观测数据进行质量控制,以45°间隔将方位角划分为不同象限,然后将卫星仰角增大或减小过程处于同一象限内的CNR观测数据加入LSP分析队列. 可见卫星仰角越低,直射信号与反射信号的相干性越显著,选择LSP分析队列中卫星仰角在0°~25°的CNR观测时间序列进行反演. 解算GNSS天线相位中心距水面高度Hantenna. 图4为实验期间某颗卫星CNR观测时间序列及Hantenna反演结果实例. 图4(a)中,tC/N0为三阶多项式拟合得到的趋势项,dC/N0为去趋势项后得到的波动项. 其中,dC/N0时间序列中仍可见微弱慢变趋势,即高阶tC/N0残差. 造成tC/N0在一定时间内存在起伏的原因涉及卫星端与接收机端的信号处理,以及GNSS信号在电离层与对流层传播过程中的环境影响,提高多项式阶数有助于降低tC/N0残差.但是,考虑到时域上频率较低的慢变趋势对频域上利用谱分析提取直射与反射信号相干频率的影响几乎可以忽略,故本文在去趋势项过程中仅采用三阶多项式拟合进行处理.
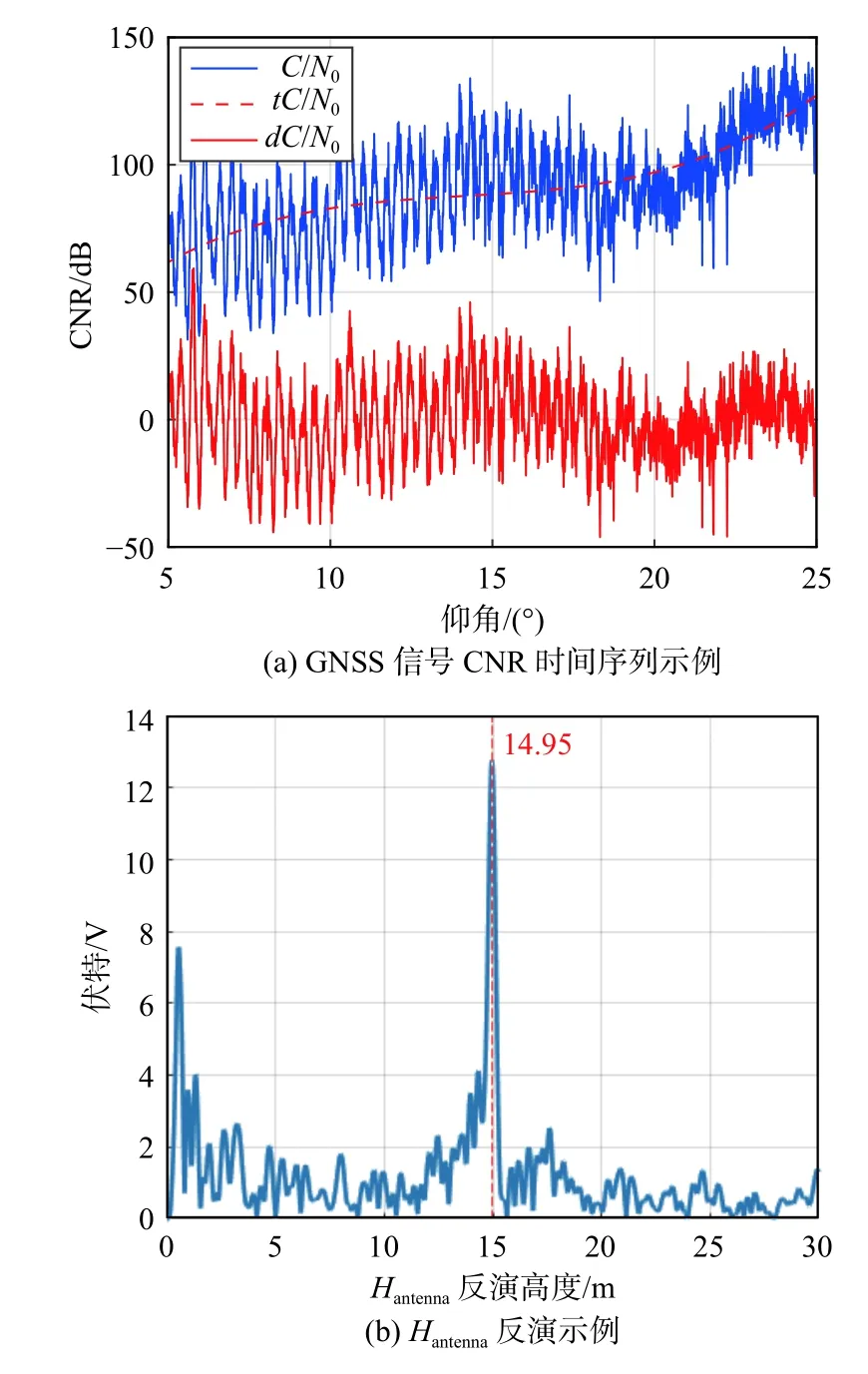
图4 卫星CNR反演 Hantenna 示例
2.3 实验结果
2.3.1 有效反演次数统计

将经过数据质控后反演获得GNSS天线相位中心到水面垂直距离Hantenna作为一次有效反演,以6 h时间窗口统计可见卫星数量和有效反演次数,结果如图5所示. 实验期间,可见GPS卫星数量较为稳定,6 h时间窗口内均值大于19颗. 由于数据质控滤除了上升与下降过程跨越不同方位角区域的GPS卫星CNR观测数据,在一定程度上降低了有效反演次数,6 h时间窗口内均值为9.7次. 在本实验使用的数据质控条件下,每小时至少能进行一次有效反演,同时观测GNSS多系统卫星CNR将增加有效反演次数.
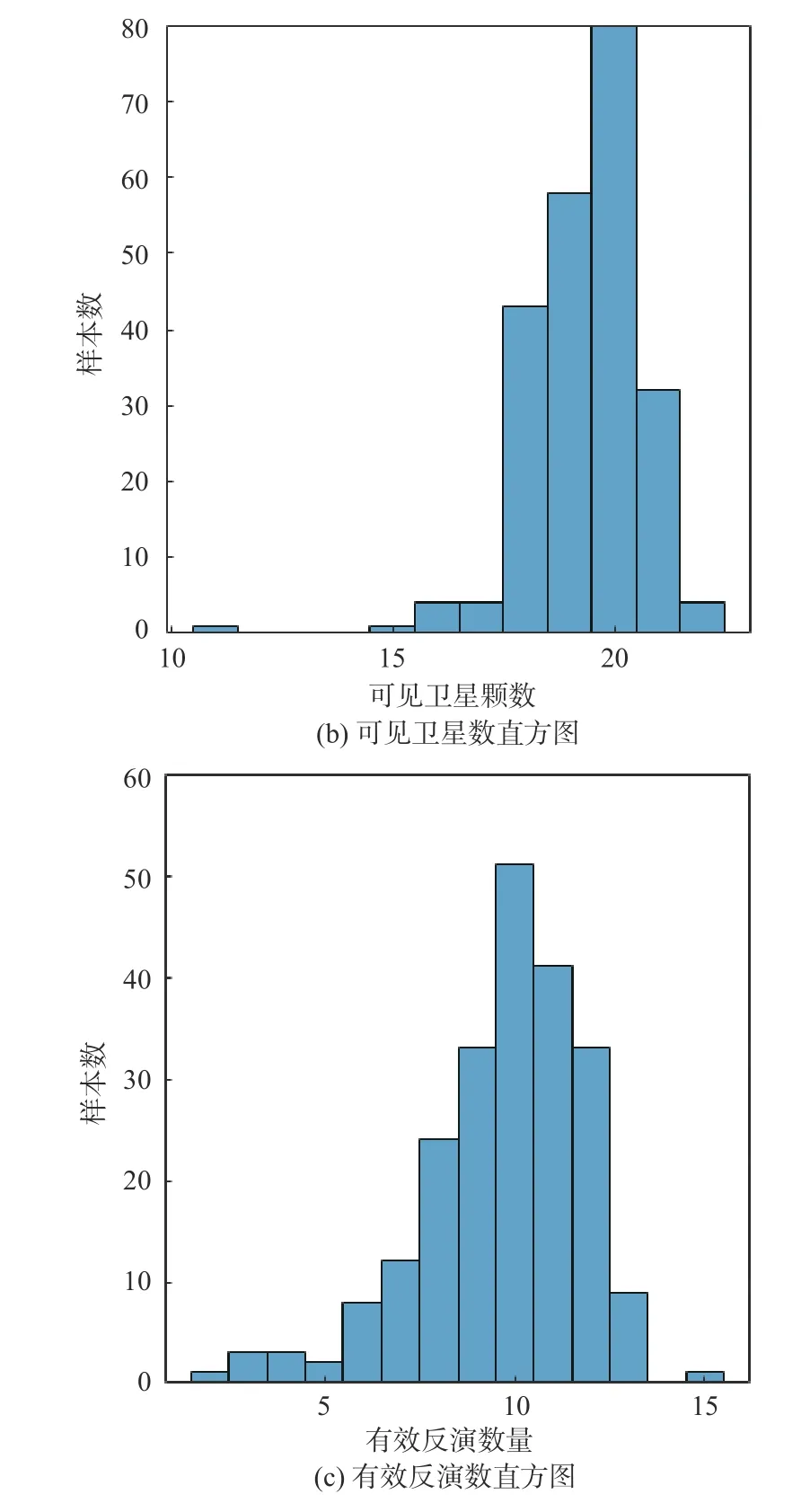
图5 可见卫星数量及有效反演次数统计
2.3.2 海况对Hantenna反演高度偏差的影响
利用实验期间同步采集的海表风速数据划分海况,分析海况对Hantenna反演高度偏差的影响,结果如图6所示. 实验期间4级、5级海况对应的样本数量较少. 各级海况条件下Hantenna反演结果最大偏差分别为0.17 m、0.21 m、0.21 m、0.22 m、0.12 m,对应Hantenna反演结果中位数在14.95~14.97 m. 由统计结果的整体趋势可见,5级及以下海况条件下,利用GNSS CNR反演Hantenna的方法受海况影响较小.
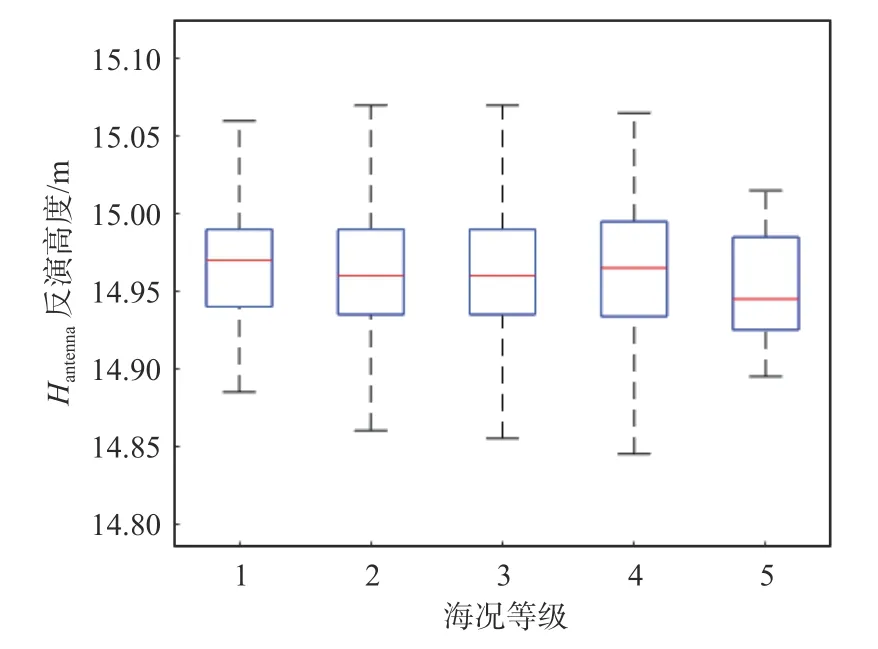
图6 海况对 Hantenna 反演高度的影响
2.3.3Hantenna反演高度时均变化
对实验期间Hantenna反演结果以1 h时间窗口进行滑动平均,结果如图7所示. 滑动平均后,Hantenna反演高度均值为14.96 m,与Hantenna设计高度的偏差为4‰;最大值15.02 m,偏差8‰;最小值14.82 m,偏差5‰.以海上蒸发波导监测预报应用为例,Hantenna反演高度偏差远小于蒸发波导监测预报模型输出的蒸发波导高度偏差,因此根据GNSS天线与船上气象要素传感器的垂直高度差值Hoffset获取船载气象要素传感器距水面高度是可行的.
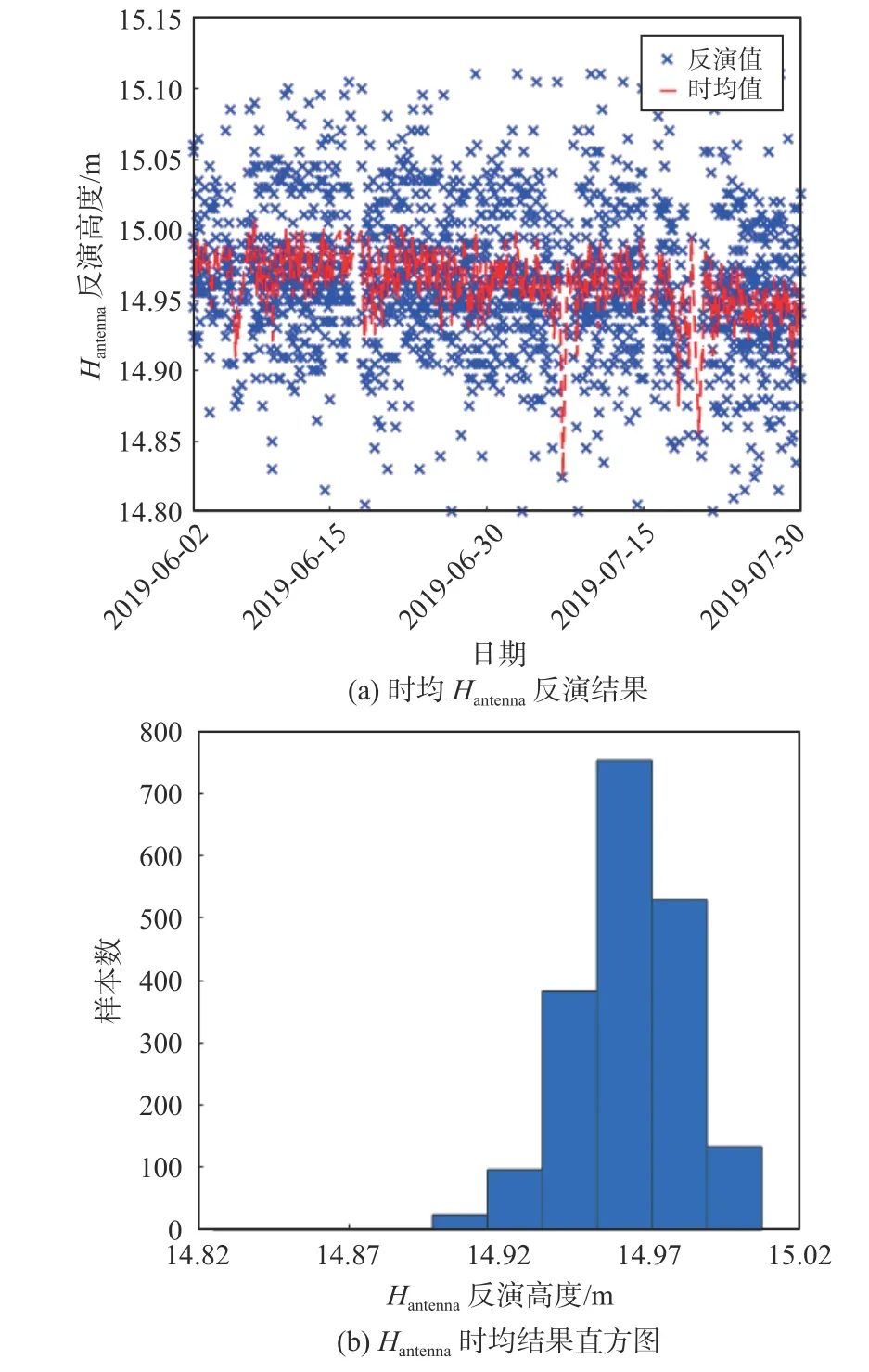
图7Hantenna 反演高度时均变化
3 结 论
船载气象要素传感器测量高度是海面蒸发波导等无线电气象参数监测系统的必要输入参数. 利用船舶GNSS设备观测卫星信号CNR,反演船载气象要素传感器距水面高度. 该方法无需安装其他外部测距设备,避免了定期清理维护测距传感器可能产生的若干问题. 趸船实验数据证明该方法能够有效反演船舶GNSS天线距水面高度并用于换算气象要素传感器距水面高度. 受卫星水面反射信号的镜面反射点与船体的距离限制,该方法更适用于开阔水域. 本文仅采用趸船实验平台对该方法的有效性进行了验证,由于实验过程忽略了船体纵横摇及升沉对传感器测量高度的影响,后期将设计实船实验进一步对该方法在实际应用场景中的实际效果进行验证.

