翼尖形状对双后掠飞翼纵向气动特性的影响

仝家豪， 张国鑫， 王 波， 马晓平

(1.中科院工程热物理研究所无人飞行器实验室，北京，100190；2.中国科学院大学，北京，100049)

减阻是飞翼设计的重要内容之一。除摩擦阻力外，诱导阻力也是飞翼阻力的重要组成部分，而减少诱导阻力，一个非常有效且便于实现的途径是选择合适的翼尖。唐登斌[1]、Hossain A[2]、Inam M I[3]、 Zhou J X[4]等人讨论了翼尖帆片、翼梢小翼以及剪切翼尖(sheared wingtip)3种翼尖装置的减阻原理和特性，其中，翼尖帆片需精心设计和大量试验验证才可实现，难度较大；翼梢小翼设计复杂性比翼尖帆片小，易于实现；剪切翼尖是一种大后掠角、大根梢比的翼尖装置，其减阻效果不如翼梢小翼，但对飞机其他性能影响小，综合效果好。相较之下，翼梢小翼和剪切翼尖是较好的选择。

对于飞翼而言，翼尖除了减阻，还需兼顾隐身性能。杨天旗发现翼梢小翼会显著增加侧向雷达散射截面(RCS)，若要在飞翼上装载，需要在翼梢小翼的材料和结构上进行合适的选择和设计[5]。因此，翼梢小翼若要兼顾飞翼隐身性能，则需增加结构和材料的复杂度；而剪切翼尖结构简单，便于应用，成为飞翼翼尖的较好选择。

相较于常规布局，飞翼布局纵向尺寸短、无平尾，导致其纵向静稳定性较差。刘志涛[6]、谢树联[7]、左林玄[8]、Gillard W[9]和Addington G[10]等研究了全动翼尖对无人机气动特性、操纵特性的影响。李林等人认为后掠式飞翼布局重心后的翼尖部分所起的作用和平尾类似[11]。

综上所述，飞翼翼尖的设计除减阻外，还需兼顾飞翼隐身性能以及翼尖作为“平尾”对飞翼纵向静稳定性的影响。故以兼顾飞翼外形隐身性能为前提，研究翼尖形状对飞翼布局纵向气动特性和纵向静稳定性的影响对飞翼布局在总体设计时翼尖形状的选择有一定的指导意义。

本文以类X-47B双后掠飞翼布局为初始外形，以基础翼尖作为对照，为兼顾飞翼隐身性能，基于边缘平行原则，设计了3种不同平面形状的翼尖。在此基础上，利用数值仿真方法研究了翼尖平面形状对飞翼纵向气动特性和纵向静稳定性的影响，以期为飞翼布局在总体设计时翼尖形状的选择提供一定参考。

1 算例验证

M6机翼作为验证CFD外部流场计算的经典案例，主要用于湍流模型的检验，例如收敛特性、精度影响等。据此，本文选择使用M6机翼来验证CFD数值模拟的可靠性。

M6数值模拟采用的是基于有限体积法的三维RANS方程求解器。湍流模型采用k-ωSST，计算选用基于压力求解和Coupled算法，使收敛速度更快[12]。M6机翼计算条件为：Ma= 0.835 9，Re= 1.172×107，T= 300 K，α= 3.06°。

图1给出CFD计算的M6表面压力系数与风洞实验值的对比。结果显示，在展向y/b=0.44位置处，CFD计算的上表面的压力系数相较于风洞实验偏小，其他位置CFD计算的数据与风洞实验数据基本吻合。

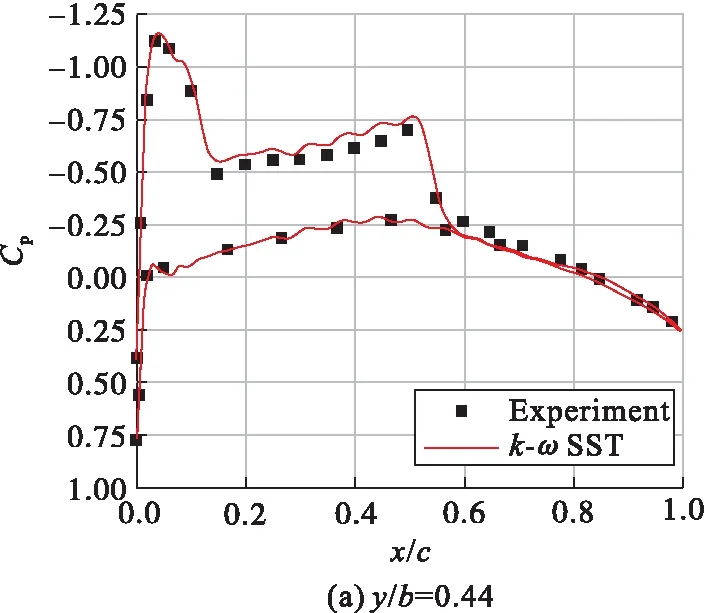
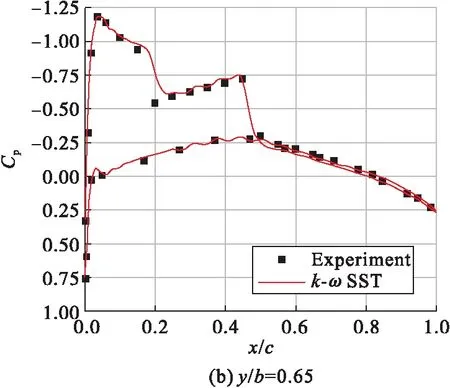
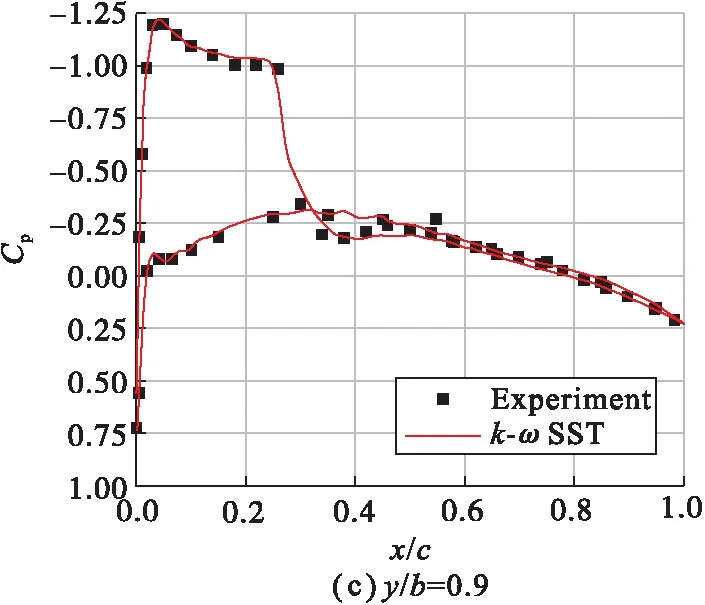
图1 M6机翼弦向压力分布

2 翼尖建模

本文的双后掠飞翼布局采用类X-47B的飞翼布局外形，见图2。模型总体参数见表1。

图2 类X-47B飞翼外形

表1 模型总体参数

飞翼在最大升阻比对应的迎角下巡航飞行，力矩参考点距头部长度为6.402 m，外翼段弦长为2.65 m。

为研究翼尖形状对双后掠飞翼布局纵向气动特性和纵向静稳定性的影响，令飞翼的内翼和外翼保持一致；令飞翼翼尖对地投影面积不变，只改变翼尖平面形状。为兼顾飞翼的隐身性能，翼尖平面形状的选取应遵循边缘平行法则。翼尖平面形状的选取如图3所示。

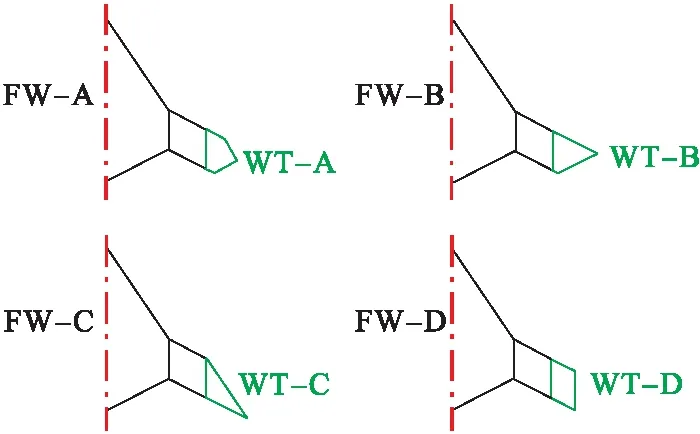
图3 4种翼尖形状

4种翼尖分别命名为WT-A、WT-B、WT-C、WT-D，其中WT-A、WT-B、WT-C是剪切翼尖，其外侧与飞翼内翼段的前缘或后缘平行；WT-D作为基准翼尖，是将外翼直接延长作为对照。与4种翼尖对应的飞翼布局分别命名为FW-A、FW-B、FW-C、FW-D。由于翼尖面积相同，平面形状不同，会导致翼尖展向长度的不同，进而导致飞翼展长和展弦比的不同。表2给出了4种飞翼布局的展长和展弦比。

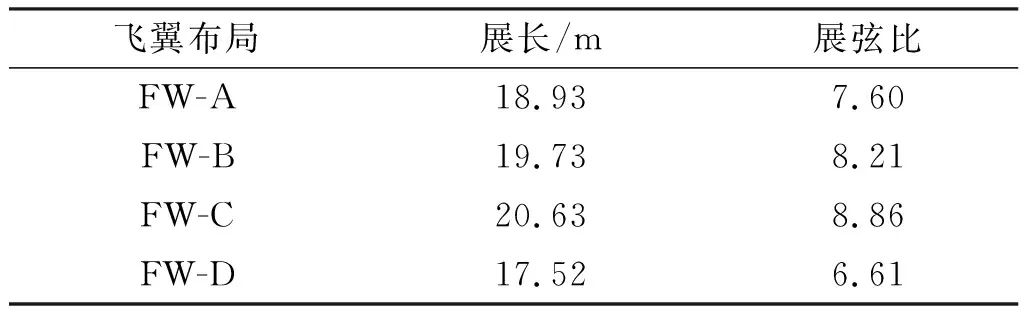
表2 4种飞翼布局展长和展弦比

3 网格划分与求解

四种飞翼布局网格均采用O型切分，图4给出FW-D模型表面网格，以飞翼对称面翼型弦长C为参考长度，计算域上、下、前、右边界距离机头长度为10C，后边界距离机头长度为20C。为捕捉飞翼布局周围的流场结构，采用渐变网格，靠近壁面网格加密，远离壁面的网格间距逐渐增大，壁面第一层的高度为5×10-6m，满足y+<1，边界层增长率约为1.2，附面层节点数为31。全流场(半模)六面体结构化网格单元数约为5.3×106，节点数约为5.2×106。

图4 FW-D半模网格

数值模拟计算采用三维可压缩N-S方程。计算过程中湍流模型采用k-ωSST，利用有限体积法对控制方程离散化，选用基于压力求解器和Coupled算法[12]。边界条件为压力远场，物面采用无滑移的边界条件，计算来流：Ma= 0.4，Re= 8.02×106，H=11 km。

4 结果与分析

图5给出4种飞翼布局的升力系数(CL)、阻力系数(CD)、升阻比(K)、俯仰力矩系数(Cm)随迎角(α)的变化曲线以及俯仰力矩系数(Cm)随升力系数(CL)的变化曲线，以探究翼尖形状对飞翼纵向气动特性和纵向静稳定的影响。

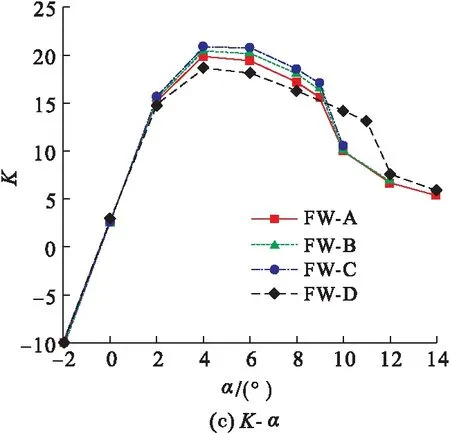
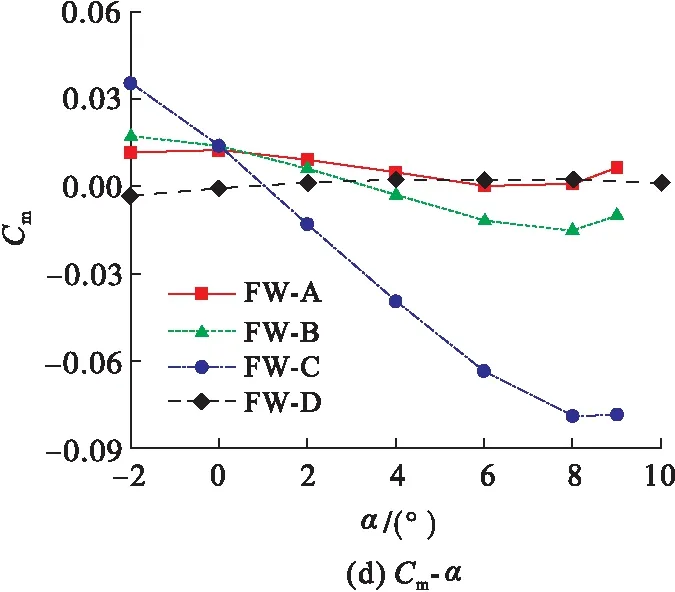
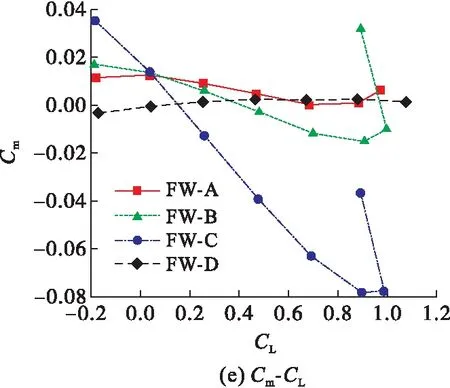
图5 4种飞翼的气动系数

4.1 翼尖形状对飞翼布局升力特性的影响

如图5(a)所示，在失速迎角范围内，翼尖形状对飞翼布局的升力特性影响并不明显，这是因为翼尖面积较小，对飞翼的升力特性影响较小。此外，FW-A、FW-B、FW-C的失速迎角为9°，而FW-D的失速迎角为11°，故相比于基准翼尖，剪切翼尖会使失速迎角提前。

4.2 翼尖形状对飞翼布局阻力特性的影响

由图5(b)可得，迎角越大，翼尖形状对飞翼布局阻力特性影响越大，3种剪切翼尖相较于基础翼尖，均能有效减小飞翼的诱导阻力。在巡航迎角4°时，相较于FW-D布局，FW-A、FW-B、FW-C 3种飞翼布局的阻力系数减少4.5%、5.3%、7.9%。自9°迎角始，FW-A、FW-B、FW-C的阻力陡增，这是因为FW-A、FW-B、FW-C在该迎角下失速，Kink点后缘发生气流分离，见图6。

图6 FW-A在9°迎角的流线图

为进一步比较各翼尖对飞翼阻力特性的影响，定义翼尖阻力系数：

(1)

式中：q为动压；FD,WT为翼尖的阻力；Sref是全机参考面积；CD,WT为翼尖的阻力系数。

图7给出4种翼尖的阻力系数对比，其中，WT-D的阻力系数最大，WT-A、WT-B次之，WT-C的阻力系数最小，并且WT-A、WT-B、WT-C在4°迎角下阻力系数为负，同时WT-C随着迎角的增加，其阻力系数减小。

图7 4种翼尖的阻力系数

为探究剪切翼尖阻力系数为负的原因，以WT-C为例，将WT-C的阻力分为压差阻力和摩擦阻力两部分，见表3。表中，WT-C的摩擦阻力系数为正，且随着迎角的增大，其数值始终比较小，且几乎不变；而WT-C的压差阻力系数为负，且随着迎角增大不断减小，最终导致WT-C的阻力系数为负值。

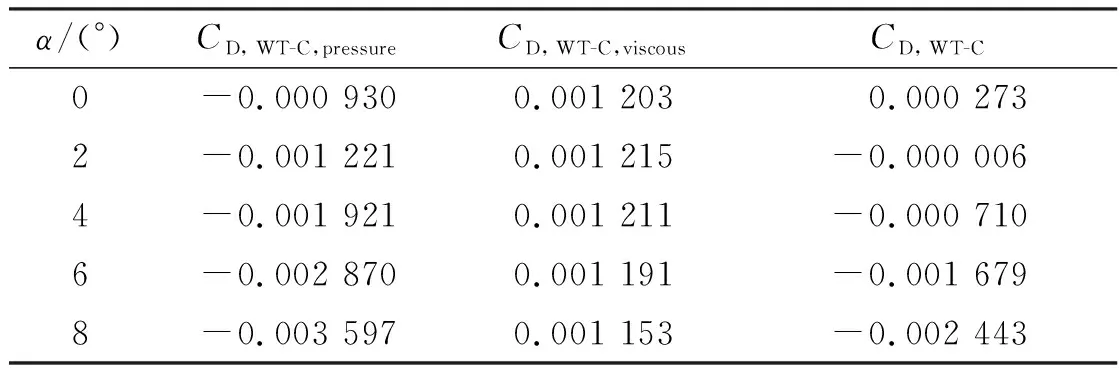
表3 WT-C的阻力系数

如图8所示，进一步的分析，剪切翼尖处在两股气流的混合流场中，一种是速度为v∞的自由来流，另一种为翼尖涡造成的侧洗流W。侧洗流场由机翼上表面向内翼方向的洗流与机翼下表面向外翼方向的洗流共同合成。自由来流(v∞)与侧洗流场(W)叠加形成局部流场(vpart)，剪切翼尖相对于局部来流产生局部升力(ΔL)，其方向垂直于局部来流；局部阻力(ΔD)，其方向平行于局部来流[13]。

图8 翼尖的气动力效应

剪切翼尖所产生的推力为：

ΔF=ΔLsinφ-ΔDcosφ

(2)

局部升力和局部阻力在来流方向的投影之和为向前推力ΔF。类似的结论与分析在江永泉的书籍中也出现[13]。

图9给出6°迎角下，WT-C及翼尖展向约2/3位置处的压力系数云图，在2/3位置处，翼型前为负压，提供向前的吸力，而翼型的尾缘压力为正，提供向前的推力，最终导致翼型的阻力系数为负。WT-C沿展向其他截面的压力分布与之类似，最终导致WT-C总的阻力系数为负。

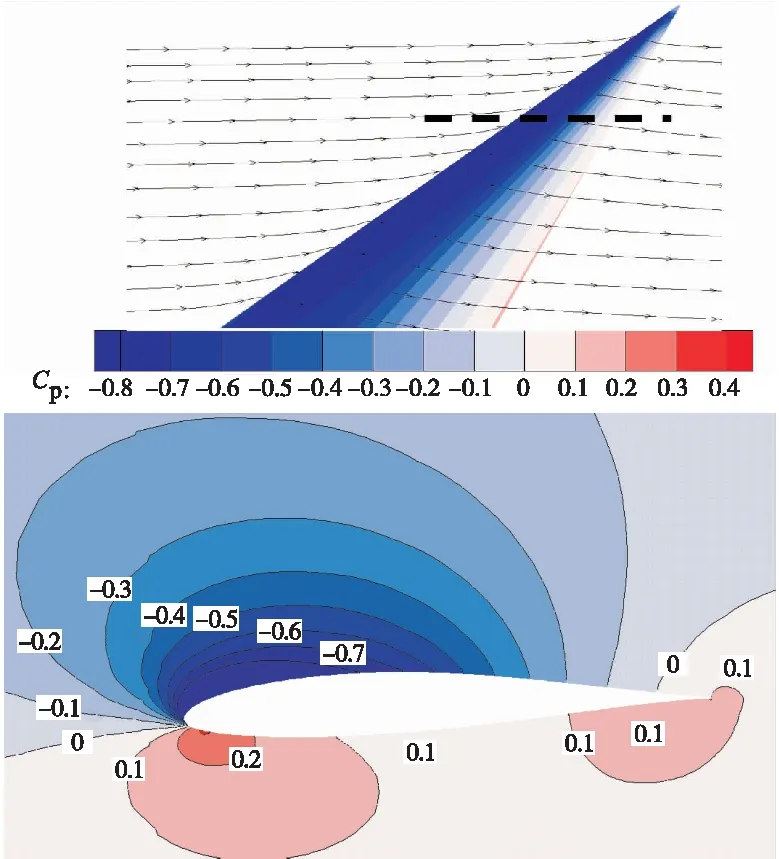
图9 6°迎角，WT-C展向2/3处平面的压力系数

4.3 翼尖形状对飞翼升阻比的影响

如图5(c)所示，迎角为4°时，4种飞翼布局达到最大升阻比。WT-A、WT-B、WT-C 3种剪切翼尖相较于WT-D分别使飞翼的最大升阻比提高6.3%、9.5%、11.9%。从展弦比来进行分析，由于λFW-D<λFW-A<λFW-B<λFW-C,当飞翼面积不变时，升阻比与展弦比成正相关，展弦比越大，升阻比越大。

实际上，根据前文对升力、阻力系数的分析，剪切翼尖形状对于全机的升力影响不大，而剪切翼尖可以减小整个飞翼的诱导阻力，故飞翼最大升阻比的提高主要因为剪切翼尖的减阻。

4.4 翼尖形状对飞翼布局纵向静稳定性的影响

飞翼纵向静稳定性的计算式为：

(3)

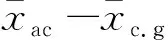
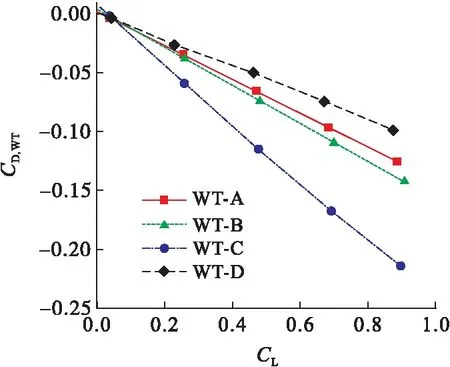
图10 4种翼尖的俯仰力矩系数

根据Cm,WT-CL的对比，WT-C翼尖增强飞翼纵向静稳定裕度的效果最好，WT-B、WT-A次之，WT-D效果最差。

FW-A，FW-B，FW-C3种飞翼布局的Cm-CL曲线在升力系数约为0.9处转折，结合Cm-α曲线可知：此时迎角为8°。图11给出FW-A在8°迎角时的流线图，可以看到，气流在飞翼的Kink点后缘区域分离，导致分离区的升力骤降；而Kink前缘的气流未发生分离，升力没有大的变化，进而产生抬头力矩，使FW-A、FW-B、FW-C的Cm-CL曲线发生转折。

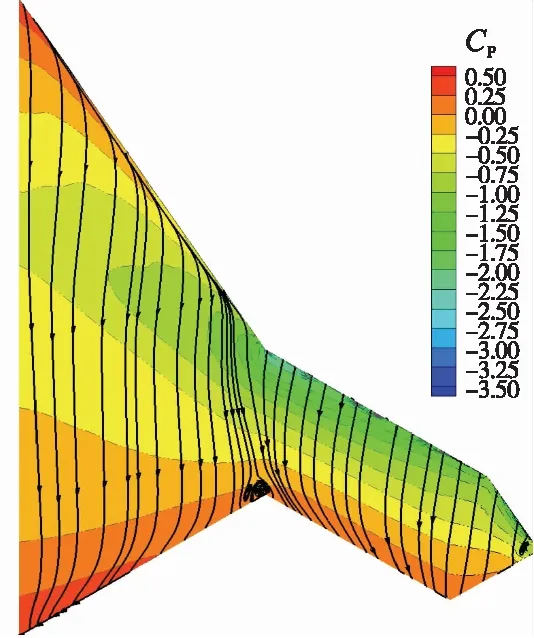
图11 FW-A在8°迎角的流线图

5 结论

以双后掠飞翼为基础外形，兼顾飞翼的隐身特性，设计4种不同形状的翼尖，得到4种飞翼布局。通过分析4种飞翼布局纵向气动特性和静稳定性，得到如下结论:

1)剪切翼尖对飞翼升力的影响较小，但是，会使飞翼的失速迎角提前。

2)剪切翼尖对飞翼全机的减阻效果显著。剪切翼尖本身的阻力系数甚至会出现负数的情况，这是因为剪切翼尖提供了向前的推力。其中，在巡航状态，相比于WT-D翼尖，WT-C翼尖可以使飞翼全机阻力降低约7.9%。

3)翼尖面积相同的前提下，剪切翼尖增加了飞翼的展长，减少了飞翼的阻力，进而提高飞翼的升阻比，相比于WT-D翼尖，WT-C翼尖使飞翼最大升阻比提高11.9%。

4)剪切翼尖的形状对飞翼的纵向静稳定性影响较大，同样的翼尖面积，WT-C翼尖使飞翼纵向静稳定裕度增加10.8%。