输入受限非线性系统的自适应零误差跟踪控制

郭雅琪， 史丽晨， 王海涛， 蒲林东

(西安建筑科技大学机械动力理论及应用研究所，西安,710055)

近年来，不确定非线性系统的控制问题在电力系统[1]、无人机系统[2-3]受到广泛的关注。实际系统中常存在不确定性，控制不确定非线性系统的难点在于，不仅要考虑系统动力学模型的强耦合、非线性特点，而且要妥善处理系统不确定性。如果在控制器设计过程中不能妥善处理系统的不确定性，不仅系统性能会受到影响，严重时甚至会危及系统的运行安全。

为解决系统的不确定性问题，国内外学者提出了很多方法，包括鲁棒控制[4]、神经网络控制[5]、模糊控制[6]等。然而，上述文献采用的方法只能实现有界跟踪，即跟踪误差收敛到零附近的紧集内，紧集的大小依赖于控制器的设计参数。换句话说，这些控制器还不能实现对参考轨迹的零误差跟踪。在某些场景下，例如精密雕刻，需要转头的位置准确跟踪上期望信号，细微的偏差可能产出工艺次品。且系统运行过程中的电压并不能保证是恒定值，因此对不确定非线性系统的零误差跟踪控制具有十分重要的实际意义。自适应控制器能够根据控制对象本身参数或周围环境的变化，自动调整控制参数以获得满意的性能，且控制系统具有强鲁棒性。近年来有学者针对不确定性非线性系统设计了渐进跟踪控制器[7-10]，例如文献[8]研究了非严格反馈形式的多输入多输出非线性系统的自适应模糊渐近跟踪控制问题，在控制器设计过程中引入模糊逻辑系统，辨识出未知非线性函数，而后基于李雅普诺夫定理，推导出跟踪误差渐近收敛至零。文献[10]针对含不确定性的一类纯反馈系统，提出了一种反步自适应控制器，可使跟踪误差渐进收敛至零。然而，上述文献没有考虑或没有很好地解决执行器输入饱和问题。

执行器输入饱和是一个在工程实际中经常发生且亟待解决的问题。尤其在实现零误差跟踪时，需要很大的执行器的输入功率。当执行器物理限制生效时，控制指令无法被完全执行，系统的性能会受到影响，严重时甚至会导致系统失稳[11]。为此，文献[12～13]设计鲁棒控制器对期望控制律进行补偿，并通过李雅普诺夫分析保证了跟踪误差的有界性。然而，据作者们所知，考虑执行器饱和的不确定性非线性系统渐进跟踪问题并没有得到很好地解决。

本文利用反步自适应控制方法，为不确定非线性系统设计了一种考虑执行器饱和的零误差自适应跟踪控制器。相较于文献[8～10]，所提方法可以考虑执行器饱和带来的不利影响，即使出现执行器饱和情形时，仍可以保证系统的稳定性。相较于文献[12～13]，所提方法可以使跟踪误差渐进收敛至零，并且从理论上证明了闭环系统的所有信号的有界性。

1 问题描述和预备知识

考虑以下具有未建模动态和输入饱和限制的不确定非线性严反馈系统[14]：

(1)

(2)

式中：umax和umin分别为u的上下界；uc为期望的控制指令。

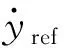
引理1[17]：对于任意正数κ和ι，下列不等式成立：

(3)

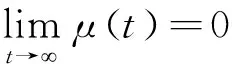
(4)

本文的控制目标是通过所提出的自适应跟踪控制器，即使在系统存在不确定动态、外界扰动以及执行器饱和的情形下，系统的输出y仍可以零误差地跟踪参考轨迹yref。

2 自适应控制器设计

本节采用反步法设计自适应控制器，控制器设计框图见图1，定义跟踪误差ei=xi-αi-1,(α0=yref)，通过设计虚拟控制器αi,i=1,2,…,n-1、实际控制器u、自适应律以及辅助误差补偿系统实现控制目标。

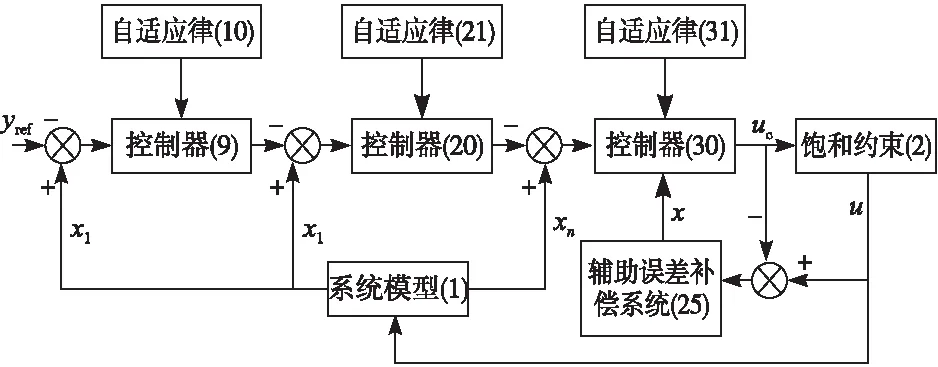
图1 控制器设计框图

第1步，由式(1)可得e1的导数为：

(5)

(6)

(7)

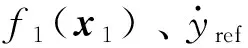
(8)

构造虚拟控制器α1和自适应律为：

(9)

(10)

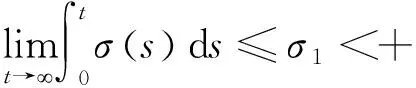
构造如下Lyapunov函数候补：

(11)

(12)

将式(9)和式(10)代入式(12)可得：

(13)

由杨氏不等式可得：

(14)

(15)

将式(14)和式(15)代入式(13)中可得：

(16)

第i步(i=2,3,…,n-1)：对ei求导可得：

(17)

(18)

(19)

构造虚拟控制器αi和自适应律为：

(20)

(21)

式中：ki、bi和ρi为正的设计参数。

构造如下Lyapunov函数候补：

(22)

(23)

将式(20)和式(21)代入式(23)，根据引理1和杨氏不等式可得：

(24)

第n步，考虑到u受到饱和约束，我们设计一种新型辅助误差补偿系统：

(25)

式中：χ为速度补偿信号；a为正的设计参数。

饱和函数sat(χ)可表示为：

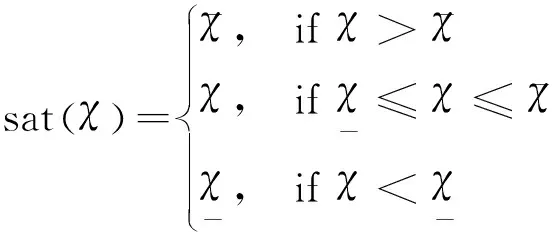
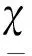
定义新的误差变量：

(26)

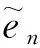
(27)

(28)

(29)

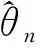
构造实际控制器uc和自适应律为：

(30)

(31)

式中：kn、bn和ρn为正的设计参数。

构造如下Lyapunov函数候补：

(32)

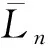
(33)

将式(25)、式(30)和式(31)代入式(33)，可得：

(34)

3 稳定性分析

证明：考虑如下的Lyapunov函数候补：

(35)

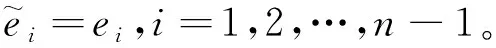
对L求导，并代入式(16)、式(24)和式(34)可得：

(36)

由式(35)和式(36)可得：

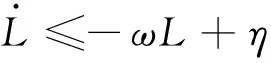
(37)

对式(37)积分可得：

L(t)≤(L(0)-η0)e-ωt+η0

(38)

式中：η0=η/ω。

(39)

将式(39)左右两端按时间积分可得：

(40)

由式(40)可得：

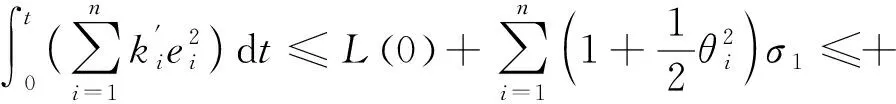
(41)

根据引理2可得：

(42)

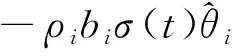
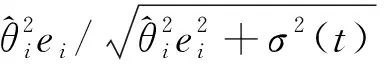
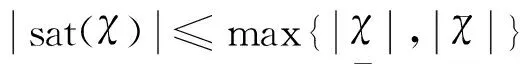
定理2：考虑辅助误差补偿系统(25)，通过合理地选择参数a，可使系统的信号χ能渐进收敛至零。

证明：考虑如下的Lyapunov函数候补：

(43)

(44)

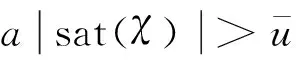
4 仿真验证

本节通过仿真验证本文所设计的控制器的有效性，以一个机电系统[19]为例，其动力学模型如下:

(45)

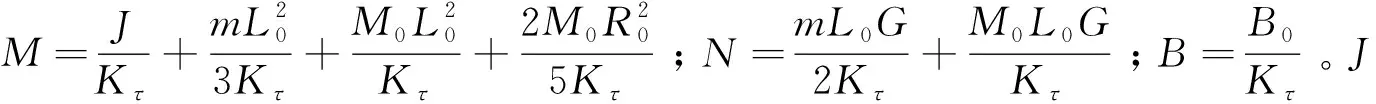
(46)

受饱和限制的执行器模型为：

(47)

为验证所提方法的有效性，将本文方法与文献[20]中提出的神经网络反步自适应方法进行比较。参考轨迹设置为yref=sin (0.5t)，所提控制器的参数设置为：

系统初值为：χ(0)=0，[x1(0),x2(0),x3(0),z]T=[-0.5,0.1,0.1,0.2]T。

采用文献[20]中提出的神经网络自适应跟踪控制方法所得的仿真如图2所示。如图所示，在设计控制器时没有考虑执行器饱和，控制输入迅速达到饱和，导致系统状态发散。这是由于系统存在初始误差，使得在开始运行时，执行器达到饱和，无法完全执行期望的控制信号。为对比所提控制器与文献[20]中的神经网络自适应控制器的跟踪误差收敛效果，在文献[20]控制器中加入式(25)、(26)，以及式(30)最后一项的抗输入饱和设计，结果见图3。

图2 未考虑执行器饱和的仿真结果

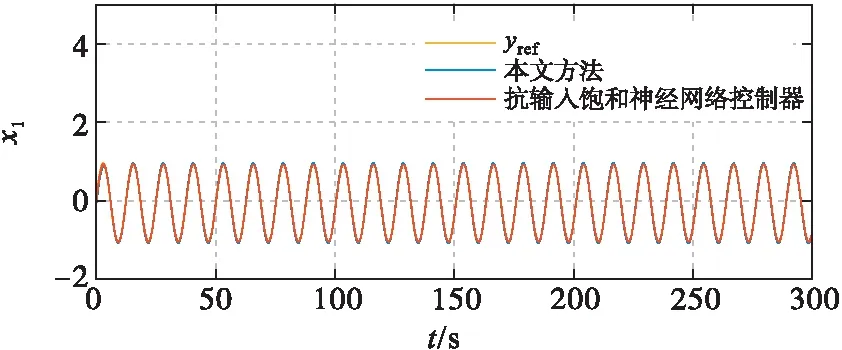
图3 系统状态x1及跟踪误差

图4显示两种方法都可保证系统的其他状态x2、x3正常变化。

图4 系统状态x2、x3及扰动z

图5为控制输入和补偿信号变化曲线，当出现输入饱和时，本文控制器产生的误差补偿信号变化幅值更小。

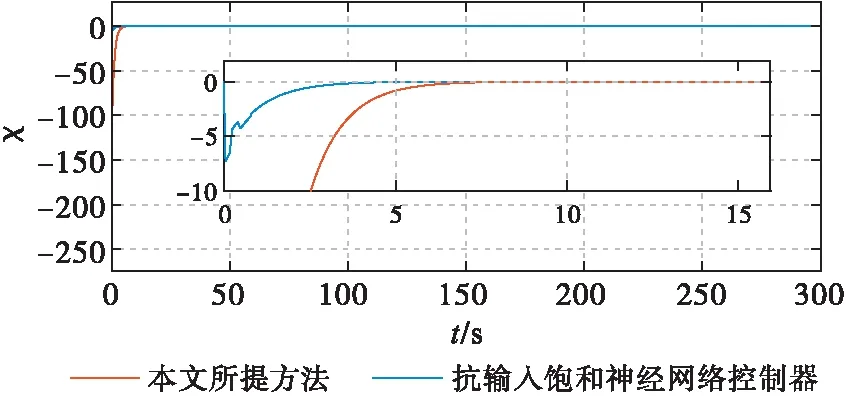
图5 控制输入u及补偿信号χ

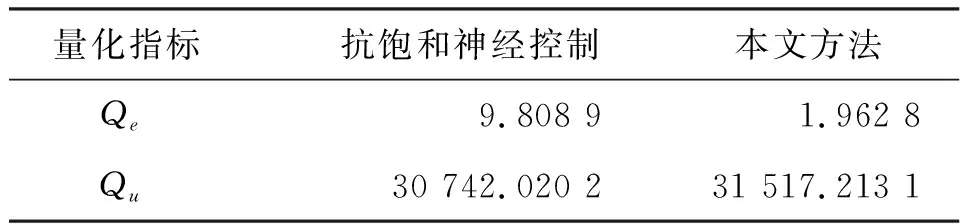
表1 跟踪误差和控制输入量化指标

图6 自适应参数

图7为3种方案所得到的跟踪误差和控制量，可见本文提出的方法跟踪精度高且能有效缓解抖振现象。

图7 3种方案下的跟踪误差和控制输入

5 结语

本文针对控制输入受限、未建模动态以及未知外界扰动影响下非线性系统的零误差跟踪控制问题，设计了一种考虑输入饱和的自适应零误差跟踪控制器。利用所提控制方法，不仅保证了闭环系统的稳定性，而且可以使跟踪误差渐进收敛至零。本文的自适应控制器中引入了抗饱和辅助误差补偿系统，在出现输入饱和时能够使系统稳定。未来的研究工作将考虑执行器速率饱和的情形下，非线性系统的零误差跟踪控制问题。

附录：

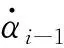
(48)

根据式(17)，我们可以将式(48)重写为：

(49)

相似地，我们可以推导出αi,(i=2,3,…，n-1)有界。