基于战场态势变权的空中集群威胁评估

李 威， 卢盈齐， 范成礼， 朱晓雯

(空军工程大学防空反导学院， 西安， 710051)

在联合空中作战中，为了提高指挥协同的效率，实现作战效能的最大化，集群作战已经成为现代空中作战的主要作战样式[1]。威胁评估作为作战过程的重要环节，对于后续的兵力部署和指挥决策具有重要意义，但目前对于空中目标威胁评估的研究大都停留战术层次，即仅考虑目标数量较少的情况下对空中目标进行威胁排序，如文献[2～8]采用了多属性决策、直觉模糊集、神经网络、支持向量机和贝叶斯网络等方法，选取了目标类型、航路捷径、飞行速度和飞行高度等目标属性对单个来袭目标进行威胁评估和排序。在联合空中作战中，以有人机和无人机组成的空中集群已经成为联合空中作战的基本作战单元，因此，当前应从战役层次对空中集群的威胁度进行合理有效的评估，这对于联合空中作战的指挥决策具有重要意义。文献[9]通过最小球覆盖算法实现基于作战范围的群威胁评估，并运用作战节点战场价值熵权重实现基于打击能力的群威胁评估，但仅考虑作战范围和打击能力显然不够全面。本文根据联合空中作战实际，建立了空中集群威胁评估指标体系，构建了一种从单机到集群的层次聚合模型对空中集群威胁度进行量化，针对常权评估无法反映战场态势动态变化的问题，引入变权理论根据战场态势确定指标变权权重，针对灰色关联分析和TOPSIS法排序结果不一致以及传统评估方法没有考虑决策者心理因素的问题，构建了基于后悔理论的灰色TOPSIS威胁评估模型。最后通过仿真验证了方法的可靠性。

1 指标体系的建立与量化

1.1 空中集群威胁评估指标体系

根据联合空中作战中空中集群的作战特点，对其威胁评估主要针对其作战效能，因此，为了充分反映空中集群的威胁程度，选取指标体系如图1所示。

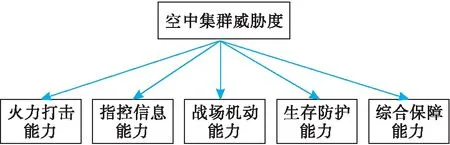
图1 空中集群威胁评估指标体系

1.2 构建威胁指标量化模型

根据联合空中作战的原则和空中集群的构成特点，将空中集群分为单机、编组和集群3个层次，同时根据离散信源和武器装备的相似性原理，构建从单机到集群的层次聚合威胁指标量化模型，进而得到集群的威胁属性值。

1.2.1 单机威胁度

单机的威胁度可通过作战效能进行反映，文献[10]提出根据离散信源与武器装备的相似性原理使用作战概率度量武器装备的作战效能，武器装备达成某一作战效果的概率越大，则该作战效果对应的作战效能也越大，对应的威胁程度也越大。因此，类比自信息模型构建单架飞机的威胁度模型为:

Iaj=-In(1-p(aj))

(1)

式中：Iaj为单架飞机在第j个指标下的威胁度；p(aj)为单架飞机取得该指标下作战效果的概率。火力打击能力中p表示飞机的命中毁伤概率；指控信息能力中p对于飞机雷达设备指发现概率，对于飞机通信装备指通信无误率等；生存防护能力中p指防护概率；战场机动能力中p指突防概率和战场支援能力等；综合保障能力中p则按提供持续作战的能力进行计算。

1.2.2 编组威胁度

根据作战实际，作战编组就是由具有同种类型武器装备的基本作战单位按照一定的组成和规模构成的能够执行一定任务的作战部队，因此将空中集群中的同类飞机作为一个编组进行处理，由于编组内飞机类型相同且规模不大，因此其威胁度可以近似通过线性叠加的方式得到。然而，飞机编组的作战能力受部署方式和协同能力的影响，在通过线性相加得到威胁度之后需要进一步引入协同系数进行修正。其线性叠加公式为:

Iij=NiIaj

(2)

式中：Iij为第i类飞机在第j个指标下的威胁度;Ni为集群中第i类飞机的数量。

1.2.3 集群威胁度

一个空中集群往往由多个编组所组成，不同编组包含的飞机类型不同，对指标威胁值的重要性不同，如轰炸机编组和电子干扰机编组由于作战强度不同对于火力打击能力的贡献度不同，对于威胁度的贡献度也不一致，且聚合函数需要满足连续性假设、边缘递减效应和量纲一致性的要求，而线性相加不满足此类情况，因此本文采用幂指数模型将不同编组的威胁度进行聚合，得到集群威胁度的公式为:

(3)

式中：K为一致性调整系数，起着调整数量级的作用;Ej为空中集群在第j个指标的威胁度;m为集群中编组数量;αij为幂指数，反映第i个编组对于第j个指标的重要性。

另外，在联合空中作战中，空中集群往往是由多军兵种的不同类型飞机所组成，编组内和编组间都是通过协同遂行各种作战任务，因此联合空中作战中空中集群威胁度的聚合不能简单地相加或相乘，需要引入协同度进行修正。协同系数作为联合作战中编组空间及作战力量规模一定的情况下反映编组内和编组间协同能力的数量表示[11]，其公式为:

(4)

式中：eij为第i个编组的第j项协同度值，包括编组的火力协同、时间协同、空间协同和信息协同等；αij和βij分别表示eij的最大值和最小值；λi为第i个编组在空中集群的权重。

通过协同系数修正得到最终的空中集群指标威胁量化值为：

Zj=ρEj

(5)

2 基于战场态势变权的指标权重

2.1 变权基本理论

变权理论[12]认为指标权重应随指标状态值的变化而进行相应改变。通过战场态势的不同对相应指标权重进行惩罚和激励变权，使其能够反映复杂多变的战场态势，增强威胁评估的合理性和科学性。

假设目标属性状态向量为X=(x1,x2,…,xn)，常权向量为ω=(w1,w2,…,wn)，变权向量可看作目标状态向量与权系数向量的函数wi(x)，满足：①归一性，各个权重值wi(x)之和等于1；②连续性，wi(x)关于每个状态变量连续;③激励性，wi(x)关于wi单调递增;④惩罚性，wi(x)关于wi单调递减。其中，满足①③即为激励性变权；若满足①、②、④则为惩罚性变权[13]。

2.2 主客观博弈组合确定指标常权

确定指标常权的方法主要包括主观赋权法和客观赋权法，其中主观赋权法主要有层次分析法(AHP法)、Delphi法和环比评分法等，该类方法主要依托专家打分进行指标赋权，但受专家的主观经验影响较大；客观法包括熵权法、因子分析法、变异系数法等，该类方法的权值主要由数据所决定，能够充分地反映客观数据中包含的分辨信息，但受数据波动的影响较大。为了使赋权结果更加合理，本文采用博弈论的思想将主客观权重进行综合得到指标常权权重。

2.2.1 层次分析法确定主观权重

Step1：假设有n个评估指标，对威胁评估指标采用两两比较的方式构建判断矩阵；

Step2：对判断矩阵进行一致性检验，若一致性比例RC小于0.1，则认为判断矩阵的一致性可以接受，否则对判断矩阵进行调整；

(6)

式中：λmax为判断矩阵的最大特征值；n为指标数量；RI为平均随机一致性指标。

Step3：根据判断矩阵的特征向量求出指标主观权重向量ω=(w1,w2,…,wn)。

2.2.2 熵权法确定客观权重

Step1：假设有m个待评估空中集群，评估指标共有n个，则威胁属性值矩阵为:

其中:zij为第i个评估集群在第j个指标下的威胁属性值。

Step2：第i个指标的信息熵为:

(7)

Step3：得到第i个指标的熵权为:

(8)

2.2.3 博弈组合确定常权权重

线性加权法是一种常见的组合赋权法，但组合系数的确定没有具体的标准，主观性较强，针对这一问题，本文采用通过博弈论的思想进行组合赋权，其原理是将主观权重作为双方博弈的一方，将客观权重作为博弈的另一方，当博弈双方达到纳什均衡状态时得到的指标权重最合理，且主观权重和客观权重的离差之和最小。具体步骤为：

Step1：将主观权重ω和客观权重v线性组合得到的指标常权权重为:

(9)

式中：λ1、λ2为线性组合系数。

Step2：根据博弈论思想，建立η与ω和v离差和最小的目标函数为：

min(η-ω2+η-v2)=

min(λ1ω+λ2v-ω2+λ1ω+λ2v-v2)

s.t.λ1+λ2=1,λ2,λ1λ2≥0

(10)

Step3：根据微分原理，使上述目标函数最小需要满足的一阶导数条件为:

(11)

标准化处理得:

(12)

λ得到最终指标常权权重为:

(13)

2.3 确定指标变权权重

博弈组合权重虽然能够兼顾专家主观经验和指标客观数据，得到较为合理的权重，但当空中战场态势发生变化时，常权评估无法反映战场态势的特点和动态变化，容易造成评估结果的不合理。通过变权理论构造状态变权向量，计算相应战场态势下不同空中集群的指标变权权重，能够得到更加科学的威胁评估结果。具体步骤为：

Step1：确定指标常权。由2.2节中的博弈组合赋权法得到指标的常权为η=η(η1,η2,…,ηn)。

Step2：构建状态变权向量。分析联合空中作战态势对我方造成的威胁可以发现，不同的作战态势会直接影响不同指标对于威胁评估的重要性程度，比如在敌方进行战略空袭的作战态势下，火力打击能力和战场机动能力的作用更加突出，对我方威胁的影响也越大，应做激励性变权处理；而在空袭态势下指控信息能力和生存防护能力对威胁程度的影响相比就会下降，应做惩罚变权处理；综合保障能力的作用在空袭态势下变化不大，可做常权处理处理，但由于需要满足权重归一化条件，因此也会相应变化。另外，不同空中集群由于在同一指标下的威胁值不同，惩罚和激励的幅度也需要与威胁值的大小相适应。

根据上述分析并结合作战实际构建第i个空中集群的状态变权向量为：

(14)

式中：m为空中集群数量；K1为激励幅度系数；K2为惩罚幅度系数；zij为第i个空中集群在第j个指标的威胁属性值；s1,s2,s3分别为激励变权指标集合、常权指标集合和惩罚变权指标集合，根据战场态势进行确定。

Step3：得到各空中集群的指标变权向量为：

(15)

式中：W(Ti)为第i个空中集群的指标权重向量。

3 基于灰色TOPSIS法的威胁评估模型

TOPSIS法是一种计算被评估目标与理想方案的相对距离进行排序的方法，而灰色关联分析则是通过计算被评估目标与正、负理想解的曲线关联度对目标进行排序的方法[14-15]。在威胁评估过程中如果单独采取其中一种方法可能得出不一样的评估结果，容易给指挥员的决策带来干扰。针对这一问题，本文建立了灰色TOPSIS法的威胁评估模型，综合考虑被评估目标与正、负理想解的相对距离和曲线关联度，且能够根据指挥员的主观意愿灵活调整偏好程度。

另外，传统的多属性决策方法是建立在决策者完全理性的基础上，没有考虑决策者的心理行为因素，而实际中决策者由于具有一定的心理偏好，不可能保持完全理性。针对这一不足，引入后悔理论[17]对灰色理想解法进行改进，决策者在决策时会遵循后悔规避原则，对将产生的后悔和欣喜进行估计，尽量避免选择使其后悔的方案。通过上述分析得到威胁评估具体步骤为：

Step1：确定威胁隶属度矩阵的正负理想点。

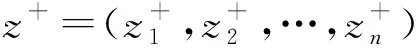
Step2：计算感知效用值。

根据期望效用理论，决策者的感知效用值随着欣喜值和后悔值的变化产生波动，由本身的效用值、后悔值和欣喜值3部分组成，第i个空中集群的感知效用表达式为：

(16)

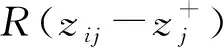
以正理想点作为参考计算待评估集群的后悔值为:

(17)

以负理想点作为参考计算待评估集群的欣喜值为:

(18)

式中：δ(δ⟩0)为后悔规避系数，δ越大则决策者的后悔规避系数越大。

根据后悔和欣喜值得到感知效用矩阵为:

其中uij=zij+hij+vij。

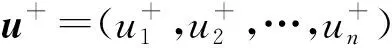
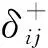
(19)

(20)

式中：ρ为分辨系数，通常取0.5。

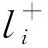
(21)

(22)

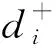
(23)

(24)

Step7：计算综合贴近度

被评估集群与正、负理想解的贴近度分别为:

(25)

(26)

式中：ω为偏好系数，反映了欧式距离和曲线形状在评估中所占的比重大小。ω越大则曲线形状的比重越大，ω越小则欧式距离的比重越大。

得到综合贴近度为:

(27)

根据综合贴近度对空中集群进行排序，综合贴近度越大，说明集群的威胁程度越大，反之说明威胁程度越小。

4 仿真分析

4.1 仿真实验

假设在联合空中作战中发现了大规模的来袭目标，经过处理得到6个空中集群及其具体信息。受篇幅所限，本文仅显示第1个空中集群的兵力组成及作战效果概率情况见表1。

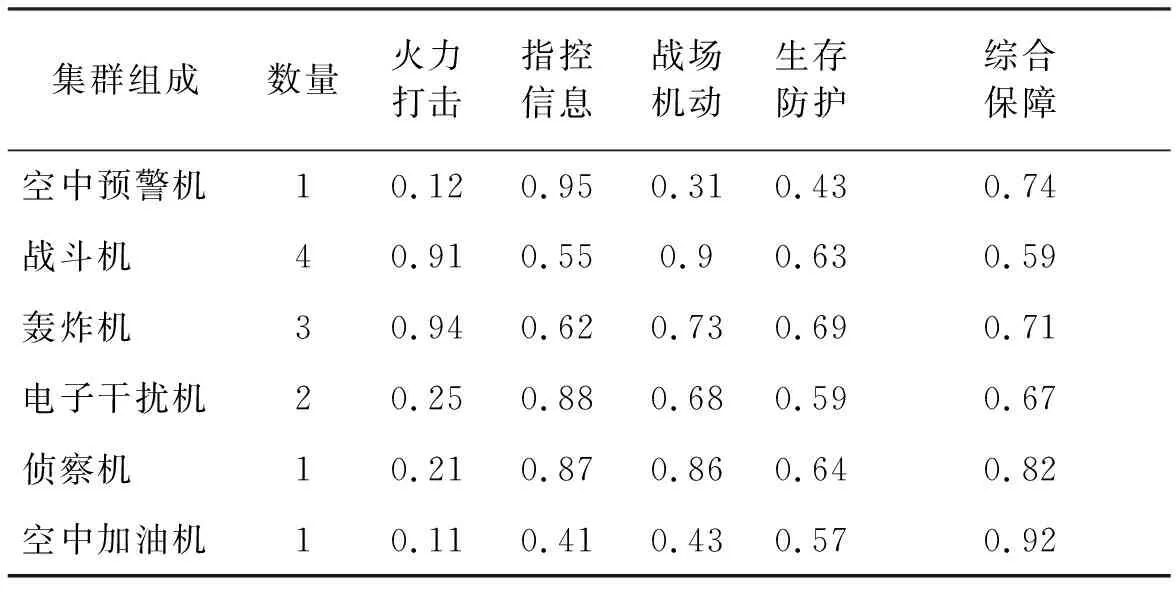
表1 空中集群信息

由式(1～2)得到编组威胁度矩阵为:

由于本文采用作战概率衡量作战效能，因此取一致性调整系数K为1，由式(3～5)得到该集群的威胁属性值向量为：

(5.570 4,4.210 2,5.052 2,2.391 7,3.277 9)

同理可计算其他5个空中集群的威胁属性值向量，得到威胁属性值矩阵为:

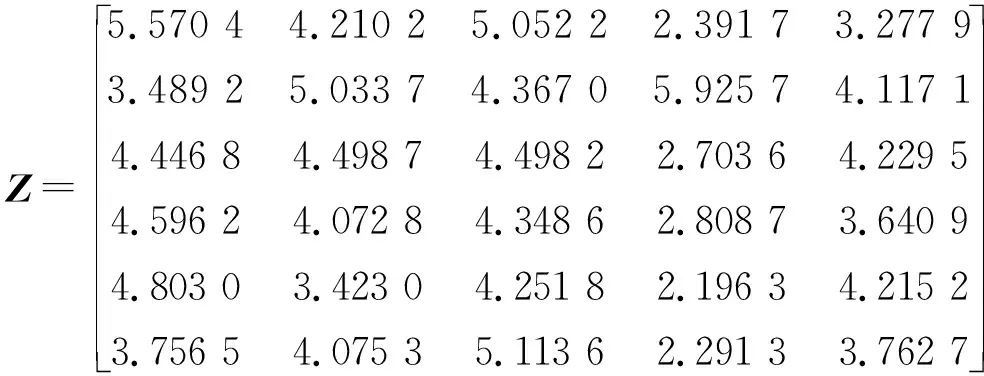
根据层次分析法得到主观权重为:

(0.398,0.263,0.136,0.125,0.078)

由式(7)～(8)得到客观权重为:

(0.378,0.096,0.212,0.183,0.131)

由式(9)～(12)得到线性组合系数为:

由式(13)得到指标常权权重为:

(0.393,0.219,0.156,0.140,0.092)

若当前我方防空部队报告发现敌发射了大量的巡航导弹和TBM，可以判断当前战场态势为遭敌战略空袭。由式(14)～(15)得到各空中集群的指标变权权重见表2。

表2 指标变权权重

取后悔规避系数为0.5，由式(16)～(18)得到感知效用矩阵为：

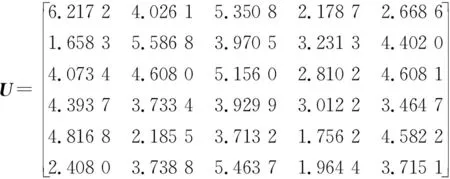
由式(19)～(24)得到加权灰色关联度和加权欧式距离如表3所示。

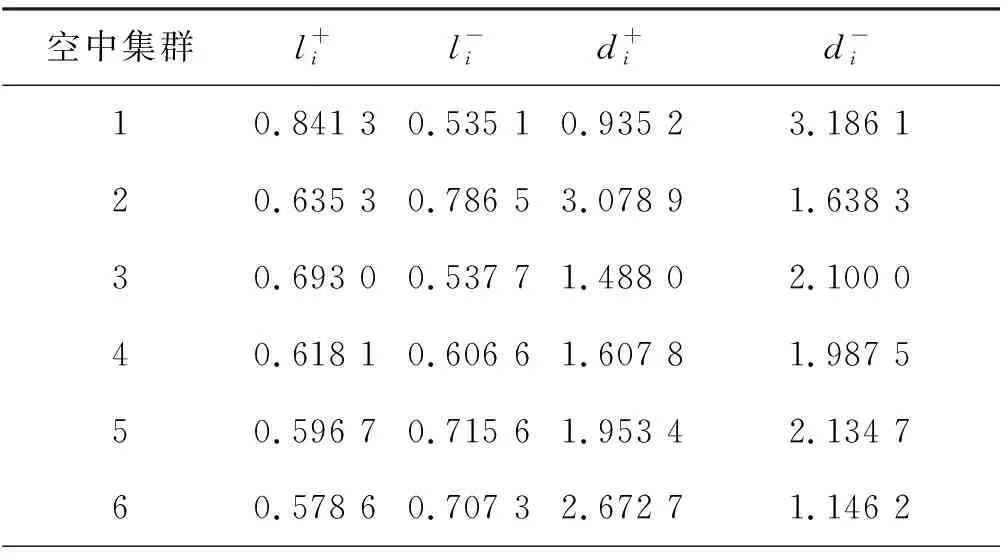
表3 加权灰色关联度和加权欧式距离

取偏好系数为0.5，表示欧式距离与曲线关联度同样重要，由式(25)～(27)得到综合贴近度为：

(0.685 5,0.388 1,0.567 0,0.521 2,0.481 7,0.369 5)根据综合贴近度得到威胁评估结果为集群1>集群3>集群4>集群5>集群2>集群6。

4.2 对比分析

4.2.1 评估方法对比分析

为了验证本文采用的灰色TOPSIS法的有效性和灵活性，分别取不同的偏好系数得到的评估结果见图2所示。

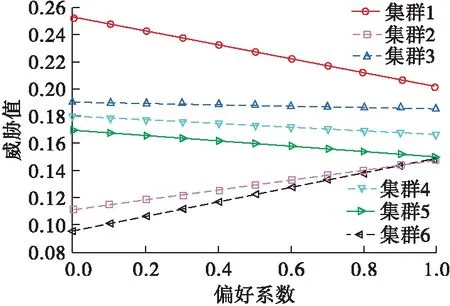
图2 不同偏好系数对比

由图2可以看出，当偏好系数取0时，方法退化为TOPSIS法，得到的威胁评估结果为集群1>集群3>集群4>集群5>集群2>集群6；当偏好系数为1时，方法退化为灰色关联分析，得到的威胁评估结果为集群1>集群3>集群4>集群5>集群6>集群2，可以发现，如果单独采用灰色关联分析或TOPSIS法可能得到不同的评估结果，容易对指挥员的决策造成影响，而本文采用的灰色TOPSIS法能够兼顾欧式距离和曲线关联度，得到更加合理的评估结果，且当偏好系数为0.9时，出现了集群2和集群6的威胁结果一致的情况，此时，决策者可以此为依据对偏好系数取值进行调节，显示了评估方法的灵活性。另外可以发现，随着偏好系数的变化，威胁排序结果总体变化不大，比如威胁最大的两个始终是集群1和集群3，说明偏好系数改变并没有影响评估的客观性，并且为了得到更加客观的结果，可以选择出现频率最高的结果作为最终排序结果。

4.2.2 战场态势对比分析

为了对比战场态势对威胁评估的影响，分别在战略空袭、侦察监视、电磁干扰3种战场态势下对指标进行变权处理，取后悔规避系数和偏好系数均为0.5，分别计算3种战场态势下各空中集群的指标权重变化量见图3，不同态势下威胁评估结果见图4。

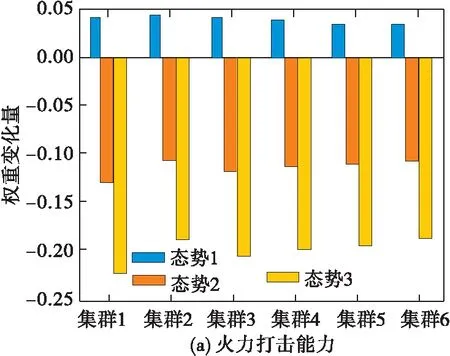
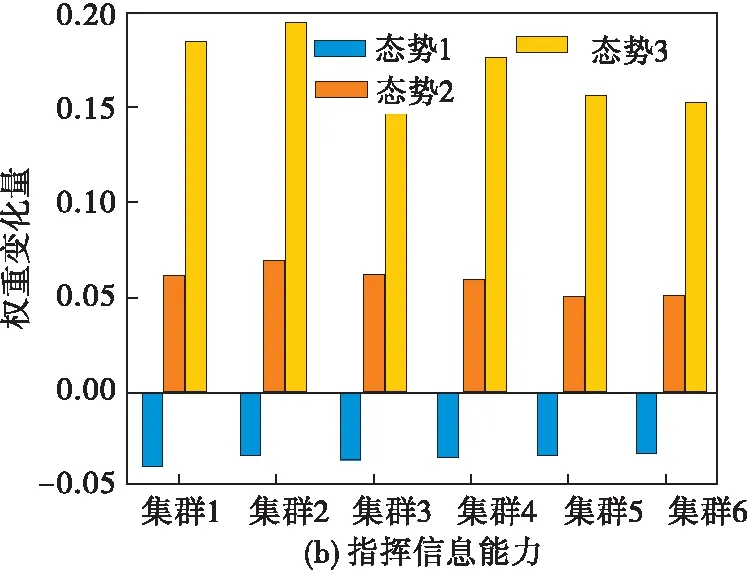
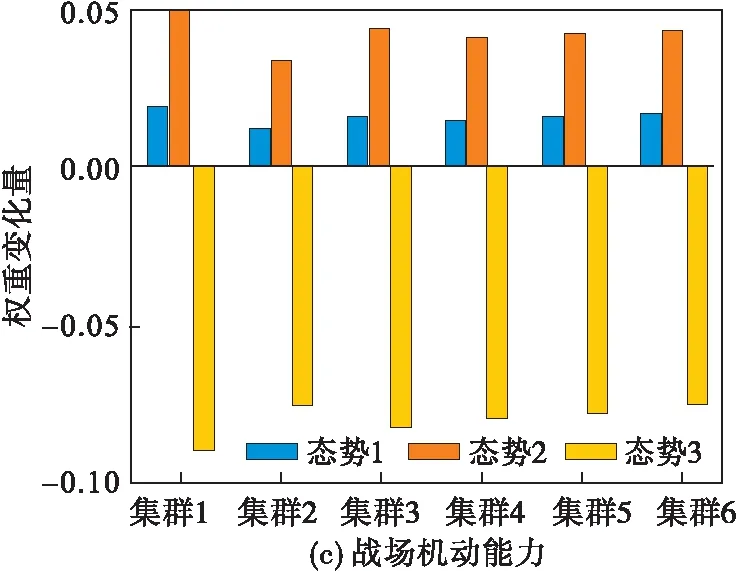
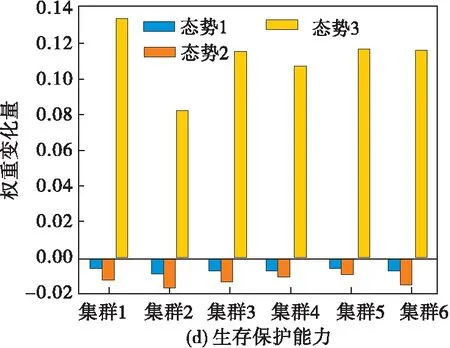
图3 不同态势下的指标权重变化量

图4 不同态势评估结果

可以看出，经过变权处理，态势1(战略空袭)中火力打击和战场机动指标权重有所增加，指控信息、生存防护和综合保障的权重有所降低，由于火力打击能力影响空袭强度，战场机动能力影响突防概率，因此火力打击能力和战场机动能力在评估中对威胁度的影响更大，其权重变化是符合战场实际的。而在同一指标下由于不同集群的属性值不同，惩罚和激励的幅度也有所不同，权重变化量也有所区别，这与战场实际相符，得到的威胁排序结果为集群1>集群3>集群4>集群5>集群2>集群6；态势2(侦察监视)中指控信息、战场机动和综合保障指标权重有所增加，火力打击和生存防护的权重有所降低，由于指控信息能力影响侦察侦察的效率，战场机动能力和综合保障能力影响侦察监视的范围，其权重的变化充分反映了态势的特点和变化，得到的威胁排序结果为集群1>集群3>集群4>集群2>集群5>集群6，说明集群2中信息类的保障飞机较多，在态势2中产生的威胁有所增大；态势3(电磁干扰)中指控信息和生存防护指标权重有所增加，火力打击、战场机动和综合保障的权重有所降低，由于指控信息能力影响干扰强度，生存防护能力影响我方打击难度，其权重变化同样也符合电磁干扰态势下的战场实际，得到的威胁排序结果为集群3>集群1>集群2>集群4>集群6>集群5。综上可以得到，通过根据态势对指标进行惩罚和激励变权能够充分反映不同战场态势的特点和变化，得到更加符合战场实际的威胁评估结果。

4.2.3 决策心理对比分析

为了分析决策者心理行为对评估结果的影响，分别在3种战场态势下选择不同的后悔规避系数进行评估，排序结果见图5。

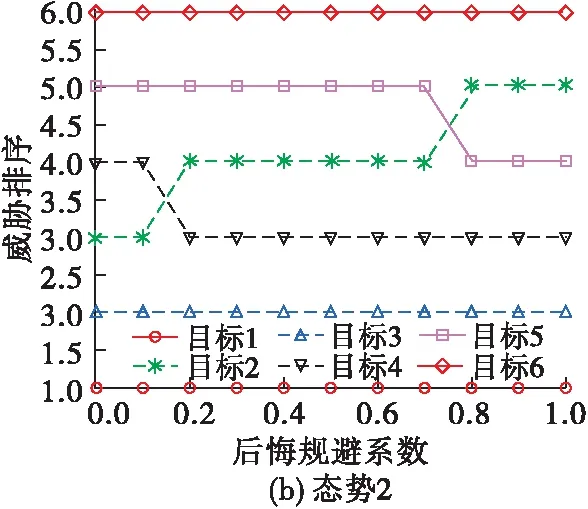
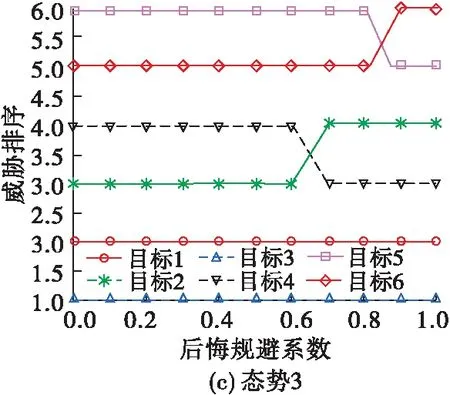
图5 不同心理行为下的威胁排序结果

由图5可以看出，在态势1中，当后悔规避系数取0.8时，集群6的威胁度超过了集群2；在态势2中，随着后悔规避系数不断增大，集群2的威胁排序不断下降，集群4和集群5的威胁排序不断升高，并在后悔规避系数分别取0.2和0.8时超过了集群2；在态势3中，在后悔规避系数取0.7时，集群4的威胁度超过了集群2，后悔规避系数取0.9时，集群5的威胁度超过了集群6。可以发现，由于不同的决策者都会根据自己的心理选择不同的后悔规避系数，因此得到的评估结果也不尽相同，说明通过引入后悔理论可以在评估中考虑决策者的心理因素，得到的结果更加符合战场实际。另外在实际作战决策过程中可能存在多个决策者共同决策的情况，这些决策者可能会选择不同的后悔系数，这时可以将多个决策者的评估结果进行综合分析进而得到最合理的评估结果。

5 结语

针对威胁评估中存在仅考虑单目标以及忽略态势对于威胁评估影响的问题，以联合空中作战为背景，提出了一种基于战场态势变权的空中集群威胁评估方法，首先构造了威胁评估指标体系和指标量化模型，采用博弈组合赋权确定指标常权权重，然后构建了反映战场态势的状态变权向量，使指标权重能够随战场态势的变化进行调整，并建立了基于后悔的理论的灰色TOPSIS的威胁排序模型对空中集群进行威胁评估。仿真结果表明，该方法在考虑战场态势的情况下对空中集群的威胁评估结果是合理和有效的，能够为指挥员的指挥决策提供科学的参考依据。