对一道平面向量问题解法的探究

张菊

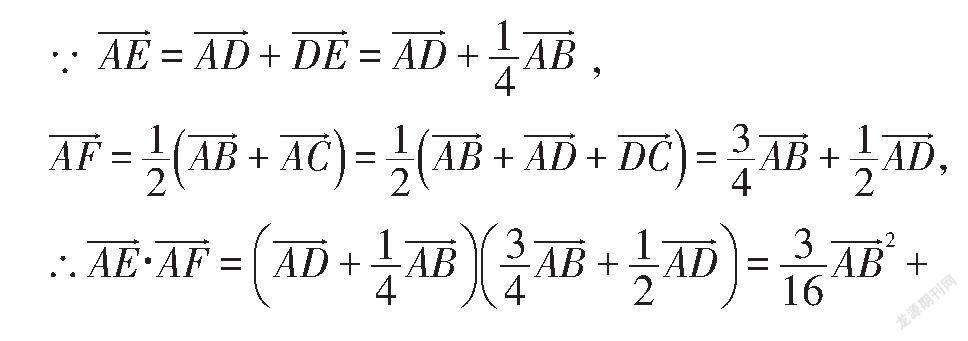
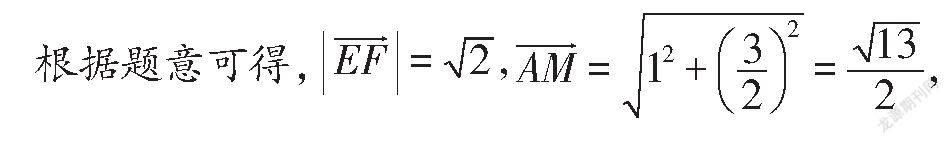
平面向量是高中数学中的重要板块.平面向量兼有“数”与“形”的双重身份，因而解答平面向量问题，可以从不同角度着手，寻找不同的解题思路.本文以一道平面向量问题为例，谈一谈解答平面向量问题的方法和思路.

解答本题，需首先明确各个点、线段的位置关系，并熟悉直角梯形的性质，抓住中点的特征，借助极化恒等式、坐标法、基底法来求解.

方法一：借助极化恒等式求解

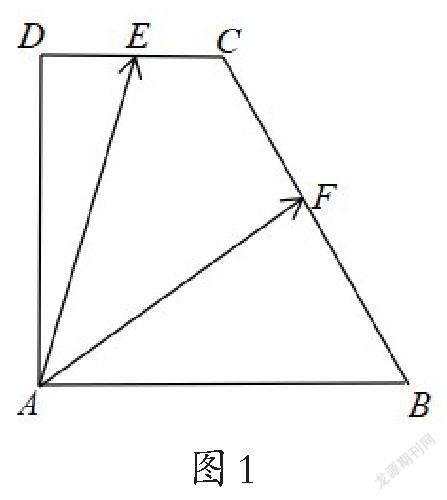
解：如图2所示，连接EF，设点M为EF的中点，连接AM，

方法二：利用坐标法求解

方法三：采用基底法求解

如果e、e是同一平面内的两个不共线向量，那么对于这一平面内的任意向量a，有且只有一对实数λ、λ，使a=λe+λe.其中，不共线的向量e、e是表示這一平面内所有向量的一组基底.因而在解答平面向量问题时，可采用基底法，根据图形的特点和题意选择一组合适的基底，分别用基底表示出各个向量，再根据三角形法则、平行四边形法则、数量积公式、模的公式等求得问题的答案.

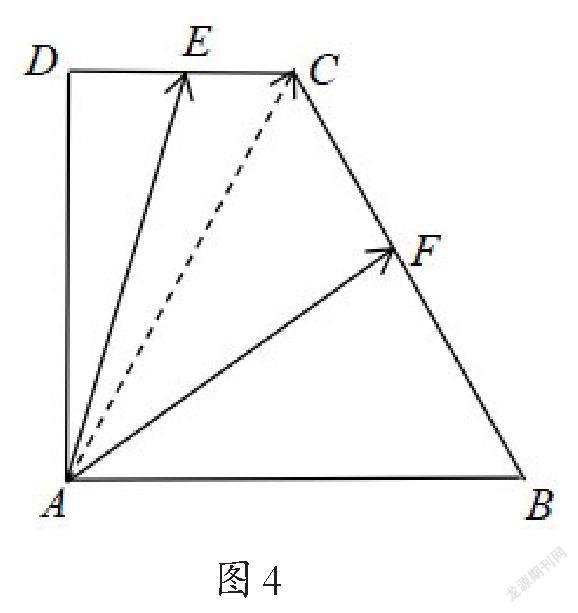
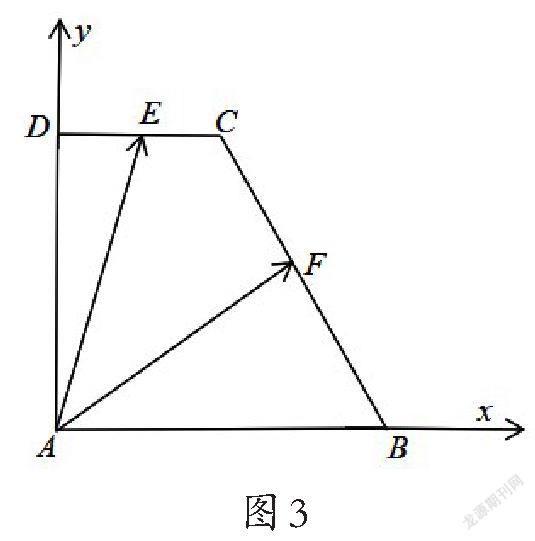
解：连接AC，如图4所示，

相比较而言，第一、第二种方法的适用范围较窄，第一种方法只适用于求解有关两个向量的积、和、差的运算问题;第二种方法只适用求解易于建立平面直角坐标系的问题.第三种方法的适用范围较广，对于一般的平面向量问题，都可采用该方法求解，但运用该方法解题时的运算量较大，并且若选择的基底不合适，有时会很难顺利解题.但无论运用哪种方法求解，都需熟练运用平面向量的运算法则、基本定理.同时适时地运用图形来辅助解题，可有效地提升解题的效率.