赵爽与《周髀算经》

吴文俊

赵爽是中国历史上著名的数学家与天文学家.他在数学上的主要贡献是为《周髀算经》写了序言，并作了详细的注释.他对《周髀算经》的研究包括三个方面：一是为书中文字作注解;二是进行较详细的数学理论推演;三是为其补图.他在序中说：“其（《周髀算经》）旨约而远，其言曲而中，将恐废替濡滞不通，使谈天者无所取则，辄依经为图，诚冀颓毁重仞之墙，披露堂室之奥.”现传《周牌算经》中的图形均为赵爽所补.

《周牌算经》是中国古老的天文学和数学著作.就其数学内容看，主要有三方面：其一，相当复杂的分数乘除运算，在开方运算中有六位有效数字的答数;其二，用勾股定理计算距离;其三，测量太阳的高度.赵爽为《周髀算经》作注释时，作过“勾股圆方图”“日高图”“七衡图”以及各种“弦图”，还用黄、朱、青三种颜色来标记图形中的不同部位.从现传本赵爽注中可以看到，他在插图上确实下过大功夫.

现用现代数学语言对“勾股圆方图”“日高图”注作出解释.为归类方便，改变了某些命题的前后次序.

一、勾股圆方图注中的命题

第一组

命题1：“勾、股各自乘，并之为弦实.”

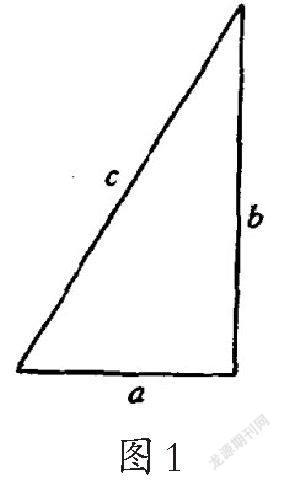
记直角三角形勾、股、弦分别为a、b、c.（如图1）

该命题是说，a+b=c.

推论：“开方除之，即弦.”

证明：“按弦图一又可以勾、股相乘为朱实二，倍之为朱实四.以勾股之差自相乘，为中黄实·加差实一，亦成弦实.”

以勾、股作为长方形的两条边，其面积是朱色直角三角形的2倍.以勾、股的差为边作中间的黄色正方形，其面积加上4个朱色三角形的面积，即为以弦为边的正方形的面积.（如图2）

第二组

命题2：“以差实减弦实，半其余，以差为从法.开方除之，复得勾矣.”

命题3：“加差于勾，即股.”

命题4：“倍股在两边，为从法.开矩勾之角，即股弦差.”

命题5：“加股为弦.”

该命题可表示为：已知a、b，求c-b、c.赵爽认为所求c-b是二次方程x+2bx=a的根，而c=b+（c-b）.

命题6：“倍勾在两边，为从法.开矩股之角，即勾弦差.”

命题7：“加勾为弦.”

这是命题4、5的对偶命题.

第三组

命题8：“凡并勾、股之实，即成弦实.或方于内，或矩于外.形诡而量均，体殊而数齐.”

这是说，以弦为边的正方形的面积是以勾、股为边的正方形面积之和.在以弦为边的正方形内截去以股（或勾）为边的正方形，余下的曲尺形面积等于以股（或勾）为边的正方形的面积.（《周牌算经》赵爽注中弦图二）二者的形状不同，然而它们的面积却是相等的.

命题9：“勾实之矩以股弦差为广，股弦并为表，而股实方其里.减矩勾之实于弦实.开其余，即股.”

命题10：“以差除勾实，得股弦并.”

命题11：“以并除勾实，亦得股弦差.”

命题12：“令并自乘，与勾实为实.倍并为法，所得亦弦.”

命题13：“勾实减并自乘，如法为股.”

由命题9可知两个正方形的面积（c+b）与a之差是以c+b与2b为边的长方形的面积之和.

第四组

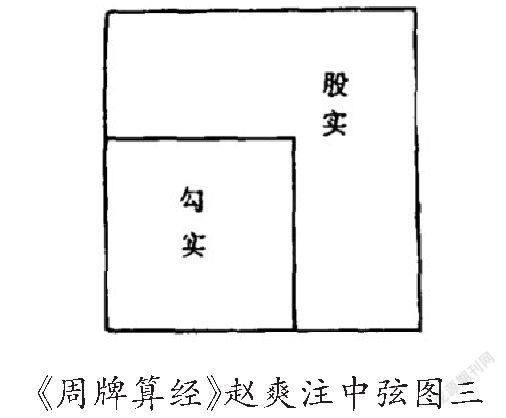
命题14：“股实之矩以勾弦差为广，勾弦并为袤，而勾实方其里.减矩股之实于弦实.开其余，即勾.”（《周牌算经》赵爽注中弦图三）

命题15：“以差除股实，得勾弦并.”

命题16：“以并除股实，亦得勾弦差.”

命题17：“令并自乘，与股实为实.倍并为法，所得亦弦.”

命题18：“股实减并自乘，如法为勾.”

命题14～18依次为命题9～13的对偶命题.

第五组

命题19：“两差相乘，倍而开之.所得.以股弦差增之.为勾.”（《周牌算经》赵爽注中弦图四）

命题20：“以勾弦差增之，为股.”

命题21：“两差增之，为弦.”

第六组

命题22：“令并自乘，倍弦实乃减之.开其余，得中黄方.”

命题23：“黄方之面，即勾股差.”

命题24：“以差减并，而半之，为勾.”

命题25：“加差于并，而半之，为股.”

证明：“以图考之，倍弦实满外大方而多黄实.黄实之多，即勾股差实.以差实减之，开其余，得外大方.大方之面，即勾股并也.”

赵爽用出入相补原理证明倍弦实、外大方与黄实之间的面积关系.（如图4）

第七组

命题26：“其倍弦为广袤合.令勾股见者自乘为其实.四实以减之.开其余，所得为差.”

命题27：“以差减合.半其余，为广.”

命题28：“减广于倍弦，即所求也.”

如果把所求长、宽视为二次方程的两根x，x那么赵爽的命题相当于：已知x+x=2c，xx=a，所求数为二次方程x-2cx+a=0的两根，而且根与系数的关系类似于韦达定理.

二、日高图注中的命题

赵爽在日高图注中用出入相补原理提出并证明刘徽公式1.

命题1：“黄甲与黄乙其实相等.”

这是说，平行四边形IT全等于平行四边形OE.由平行四边形KD及对角线KD可得以公共顶点G的平行四边形JT全等于平行四边形NE.又由平行四边形KD及對角线KD可得以公共顶点I的平行四边形JS全等于平行四边形LU.又作IU=SD=GQ，平行四边形NQ（青己）全等于平行四边形LU全等于平行四边形JS（青丙）.做一次减法得平行四边形IT（黄甲）全等于平行四边形OE（黄乙）.

命题2：“以表高（IS）乘两表相去（ST）为黄甲之实，以影差（TD2-SD1）为黄乙之广而一，所得则变得黄乙之袤（PE）.”

综合命题1、2得刘徽公式1.

由命题1可计算出两个长方形的边长，推出“日去表顶”的距离.

命题3：“按日高图加表高（得日去地）.”

证明：“青丙与青己其实亦等.黄甲与青丙相连，黄乙与青己相连，其实亦等.”

但是从现存文献看，《周牌算经》赵爽注和《九章算术》刘徽注所用数学用语非常一致，其有关证明方法也十分类似，由此可知，这些算术知识为汉魏时期数学家们的共同见识.

赵爽在数学上的贡献表现在三大方面：一是列出了一元一次方程的一个求根公式，以及由此证明了根与系数之间存在的关系;二是奠定了重差术的理论基础;三是提出了一种证明勾股定理的简洁方法油此可见，无论是在演算方法还是数学思想方面，赵爽对中国传统数学的发展都作出了重要贡献，在世界数学领域具有崇高地位.

——摘自《中国数学史大系·第三卷》